1. Spaces of Vectors
■ 선형 결합(linear combination)을 간단하게 말하면, 임의의 스칼라가 곱해진 벡터들의 덧셈이다.
■ 여기서 벡터에 곱해지는 스칼라는 벡터의 길이를 늘리는 역할을 한다. 벡터에 어떤 스칼라를 곱하더라도 벡터의 차원은 변경되지 않는다. 중요한 것은 벡터들의 덧셈이다.
■ 벡터 덧셈은 항상 크기(차원)이 같은 두 벡터에 대해서만 가능하다. 즉, 선형 결합이 '같은 공간 상에 존재하는 벡터들' 사이에 가능하다는 의미이다. 여기서 공간은 벡터 공간을 말한다.
■ 벡터 공간은 \( \mathbb{R}^1, \mathbb{R}^2, \mathbb{R}^3, \cdots \) 등으로 표기한다.
- 예를 들어 벡터 공간 \( \mathbb{R}^5 \)는 원소(성분)이 5개인 모든 열 벡터를 포함하며, 이를 5차원 공간이라고 부른다.
■ 이를 일반화하면 \( \mathbb{R}^n \)은 \( n \)개의 성분을 가진 모든 열벡터 \( v \)로 구성된 공간이라고 할 수 있다.
- 열벡터 \( v \)의 성분은 실수이므로 \( \mathbb{R} \) 문자를 사용한다.
- 만약, \( v \)의 성분이 복소수라면 \( \mathbb{C} \) 문자를 사용한다.
■ \( \mathbb{R}^2 \) 공간은 \( xy \)평면을 말한다. 즉, \( \mathbb{R}^2 \) 공간은 \( xy \) 평면 전체가 벡터 공간이다.
- \( \mathbb{R}^3 \) 공간은 \( xyz \) 평면 전체가 벡터 공간이다.
■ 그러므로 \( \mathbb{R}^2 \) 공간에서 열벡터 \( v \)의 성분은 \( (x, y) \)좌표가 된다. \( \vec{v} = (x, y) \)
- \( \mathbb{R}^3 \) 공간에서 열벡터 \( v \)의 성분은 \( (x, y, z) \),
- \( \mathbb{R}^1 \) 공간에서 열벡터 \( v \)의 성분은 직선 \( x \)축이 된다.
■ 예를 들어, 벡터 공간 \( \mathbb{R}^2 \) 공간은 \( x-y \)평면 전체가 벡터 공간이고, \( \mathbb{R}^3 \) 공간은 \( xyz \)평면 전체가 벡터 공간이 된다. 만약, 다음과 같이 벡터의 실수 성분이 5개면, 이 벡터는 5차원 공간에 속하는 벡터이다.

이러한 점이 선형대수의 장점이다. 사람이 인지할 수 없는 4차원 이상의 공간에 대해서도 다룰 수 있다.
■ 예를 들어 \( x \)축과 \( y \)축으로 이루어진 \( \mathbb{R}^2 \) 공간을 생각해보자. 위의 내용에 따라 \( \mathbb{R}^2 \) 공간은 다음과 같은 실수를 원소(성분)로 가지는 2차원 벡터들로만 구성된 벡터 공간이다.

■ 예시로 든 3개의 2차원 벡터를 2차원 벡터의 벡터 공간인 \( xy \)평면에 나타내면 다음과 같다.

■ 이때 영벡터는 2차원 벡터 공간에 표현되지는 않았지만, 분명히 \( \mathbb{R}^2 \) 공간에 있는 하나의 벡터이다.
■ 왜냐하면, 영벡터는 다음과 같이 선형 결합으로 만들 수 있으며, 이 예에서 선형 결합으로 만들어진 영벡터는 2차원 벡터들의 선형 결합으로 만들어졌기 때문에 2차원이다. 그러므로 2차원 영벡터는 \( \mathbb{R}^2 \) 공간에 포함될 수 있다.
- 아래 예시처럼 벡터 연산은 벡터 공간 안에서 이루어지며, 선형 결합을 만든다.
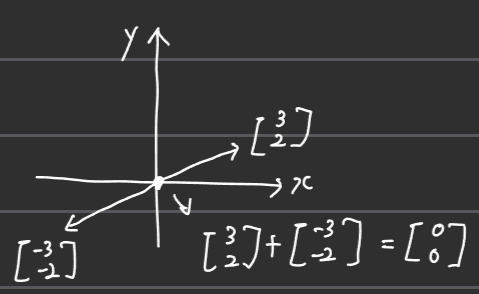
■ 이를 통해 알 수 있는 것은 모든 벡터 공간에는 영벡터가 포함된다는 것이다.
■ 반대로 영벡터가 없다고 생각해 보자. 그렇다면 위의 1·[3 2] + 1 ·[-3 -2] = [0 0]은 성립하지 않는다. 그러나 [0 0]은 [3 2]처럼 두 개의 성분을 가지는 2차원 벡터이다. 이는 다른 차원의 벡터 공간에서도 동일하다.
■ 이 예에서 중요한 것은 벡터 공간 \( \mathbb{R}^n \)에서 (모두 차원이 \( n \)인) 임의의 벡터를 더할 수 있으며, 벡터 \( v \)를 임의의 스칼라로 곱할 수 있다는 것이다.
2. Subspaces
■ 벡터 공간 \( \mathbb{R}^n \) '내부'에는 중요한 벡터 공간들이 있다. 이것을 \( \mathbb{R}^n \)의 부분 공간(subspace)라고 부른다.
■ 벡터 공간의 부분 공간은 다음 두 가지 조건을 만족하는 벡터 집합(영벡터 포함)이다.
- 벡터 \( v \)와 \( w \)가 부분 공간에 속하고, \( c, d \)가 임의의 스칼라인 경우
- (1) \( v + w \)는 부분 공간에 속한다.
- (2) \( c \cdot v \)는 부분 공간에 속한다.
■ \( v + (-w) \) 즉, \( v - w \)는 \( v \)와 \( -w \)의 벡터 덧셈으로 볼 수 있기 때문에 \( v - w \)도 부분 공간에 속한다.
■ 즉, 부분 공간 내의 벡터로 만든 모든 선형 결합 \( cv + dw \)은 부분 공간에 위치하게 된다. 또한, \( c = 0 \)이면 \( c \cdot v \)는 영벡터(zero vector)가 된다. 이 영벡터도 부분 공간에 속해야 한다.
■ 예를 들어 어떤 벡터 \( v \)가 다음과 같이 벡터 공간 \( \mathbb{R}^2 \)에 있다고 하자.

■ 이 벡터 \( v \)가 있는 공간이 벡터 공간이라면, 벡터 \( v \)에 임의의 스칼라를 곱한 벡터들도 \( \mathbb{R}^2 \) 위에 놓이게 될 것이다.

■ 임의의 스칼라를 \( k \)라고 하자. 그러면 수많은 벡터 \( k \cdot v \)가 모이게 되면 위와 같이 하나의 직선이 된다.
■ 이렇게 벡터를 하나 넣으면, 그 벡터의 모든 배수로 이루어진 전체 선이 생기게 된다. 그리고 이 선에 존재하는 어떠한 벡터들끼리 더해도 같은 선 위에 위치하게 된다.
■ 이렇게 \( \mathbb{R}^2 \) 안에 있는 부분 집합(이 예에서는 \( \( k \cdot v \)로 구성된 집합)을 \( \mathbb{R}^2 \)의 부분 공간이라고 부른다.
■ 이때 조심해야 할 것은, 예를 들어 \( \mathbb{R}^2 \)의 경우 모든 직선이 \( \mathbb{R}^2 \)의 부분 공간이 될 수 없다. 오직 원점(영 벡터)을 지나가는 직선만 \( \mathbb{R}^2 \)의 부분 공간이 될 수 있다.
■ 예를 들어 \( \mathbb{R}^2 \)에서 다음과 같은 벡터들로 구성된 원점을 지나가지 않는 직선이 있다고 해보자.
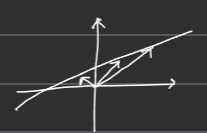
■ 이 예시에서 어떤 벡터에도 스칼라 0을 곱했을 때 직선 상에 위치하게 되는 벡터가 없다. 그러므로 이 직선은 \( \mathbb{R}^2 \)의 부분 공간이 아니다.
■ 따라서 \( \mathbb{R}^2 \)의 부분 공간은 반드시 영 벡터(zero vector)를 포함해야 한다. 그리고 이는 어떠한 \( mathbb{R}^n \)에 대해서도 마찬가지이다.
2.1 부분 공간의 합집합, 교집합
■ 부분 공간도 벡터들로 이뤄진 공간으로, 그 자체로 벡터 공간이다. 그러므로 부분 공간에서도 임의의 벡터 \( v, w \)에 대해 다음을 만족해야 한다.
- 부분 공간을 \( S \)라고 했을 때,
- 기본적으로 zero vector가 포함되어 있어야 하며
- ① \( v + w \in S \)
- ② \( c \cdot v \in S \) \( c \)는 스칼라
- ③ \( cv + dw \in S \) 선형 결합 결과가 \( S \)에 존재
■ 예를 들어, \( \mathbb{R}^3 \) 공간은 벡터 공간이다. \( \mathbb{R}^3 \) 내의 두 벡터를 더하거나 상수를 곱해도 그 결과가 여전히 \( \mathbb{R}^3 \) 공간 안에 있으며 영 벡터와 선형 결합의 결과도 여전히 \( \mathbb{R}^3 \) 공간 안에 있기 때문이다.
■ \( \mathbb{R}^3 \)의 부분 공간은 영 벡터와 원점을 지나는 직선 그리고 원점을 지나는 평면이 있다. 이 직선과 평면을 \( L \)과 \( P \)라고 하자.
■ 평면 \( P \) 위의 두 벡터를 더한 결과는 평면 안에 있으며, 평면 \( P \) 위의 벡터에 스칼라를 곱해도 여전히 평면 안에 있다. \( L \)도 마찬가지이다.
■ 그렇다면 \( P \cup L \), \( P \) 또는 \( L \) 또는 둘 다에 속하는 모든 벡터의 집합으로 이뤄진 공간은 부분 공간이 될 수 있을까?
■ 이 경우 선형 결합 결과가 \( P \cup L \)에 속하지 않기 때문에 부분 공간이 될 수 없다. \( P \) 위의 벡터와 \( L \) 위의 벡터를 선형 결합했을 때, 그 결과가 \( P \) 또는 \( L \) 또는 둘 다에 속하는 벡터가 아닌 \( \mathbb{R}^3 \) 어딘가에 있는 벡터가 되기 때문이다.
■ 반면, \( P \cap L \), \( P \)와 \( L \) 모두에 속하는 집합은 부분 공간이 된다. \( P \)와 \( L \)의 유일한 교점은 원점(영벡터)이며, 영벡터 자체는 부분 공간이기 때문이다.
■ 여기서 알 수 있는 것은 임의의 두 부분 공간에 대해 두 부분 공간의 교집합은 부분 공간이 된다는 것이다.
■ 두 부분 공간 \( S \)와 \( T \)가 있을 때, 두 부분 공간의 교집합에 속하는 벡터를 \( v, w \)라고 하자.
■ 벡터 \( v \)와 \( w \)는 교집합에 속하므로 두 벡터 모두 \( S \)에 속한다. 또한 \( T \)에도 속한다. 그리고 위의 만족 조건을 생각한다면, \( v + w \)는 \( S \)에도 속하고 \( T \)에도 속한다.
■ 스칼라를 곱한 결과도 마찬가지이다. \( v \)나 \( w \)에 임의의 스칼라를 곱한 결과는 \( S \)에도 속하고 \( T \)에도 속한다.
■ 이렇게 두 부분 공간의 교집합을 취하면 더 작은 부분 공간이 되지만, 여전히 부분 공간이 된다.
- 예를 들어 위의 \( P, L \) 예시에서 부분 공간 \( P \)는 2차원 평면, 부분 공간 \( L \)은 1차원 직선인데, 둘의 교집합인 0차원 점(또는 영벡터)은 차원이 더 작지만 부분 공간이 된다.
'선형대수' 카테고리의 다른 글
| Spaces of Vectors - (2) Column Space and Nullspace (0) | 2025.01.21 |
|---|---|
| [개념] 벡터 공간 (0) | 2025.01.20 |
| Solving Linear Equations - (4) Inverse Matrices, (5) Elimination = Factorization: A = LU, (6) Permutations (0) | 2025.01.18 |
| [개념] 행렬 (3) (0) | 2025.01.18 |
| [개념] 행렬 (2) (0) | 2025.01.18 |



