1. 벡터 공간(vector space)
1.1 공간 (space)
■ 집합 \( V \)의 임의의 원소 \( u, v \)와 임의의 스칼라 \( k \)에 대해, \( k \in \mathbb{R} \) 다음을 만족할 때, 집합(set) \( V \)를 공간(sapce) \( V \)라 한다.
\( ① u + v \in V \quad ② k \cdot u \in V \)
■ 다시 말해, 집합 \( V \)에 위의 조건 ①, ②를 모두 만족하면 집합 \( V \)를 공간 \( V \)라고 한다.
- 여기서 조건 ①이 의미하는 것은 \( V \)라는 집합 안에서 원소 \( u, v \)를 임의로 꺼냈을 때, 두 원소를 더한 값이 다시 집합 \( V \)에 속해야 한다는 의미이며 (즉 , \( V \)의 원소가 되어야 한다는 의미이다)
- 조건 ②가 의미하는 것은 \( V \)라는 집합에서 원소 1개 \( u \)를 임의로 꺼냈을 때, \( u \)에 실수 \( k \)를 곱한 값이 다시 집합 \( V \)에 속해야 한다는 의미이다.
- 조건 ①과 ②를 집합 \( V \)가 만족을 해야 그 집합 \( V \)를 공간 \( V \)라고 할 수 있다.
■ 예를 들어 다음과 같이 \( A, B \)라는 집합이 있을 때, 집합 \( A, B \)가 공간이 될 수 있는지 확인하는 방법은 다음과 같다.

- 집합 \( A \)에서 임의의 원소 \( u + v \)인 (1, 3)은 집합 \( A \)의 원소가 될 수 없다. 그러므로 \( A \)는 공간이 아닌 집합이다.

- 반면, 집합 \( B \)는 조건 ①과 ②를 모두 만족하므로 집합 \( B \)는 공간 \( B \)가 될 수 있다.
1.2 벡터 공간 (vector space) 조건
■ 공간 \( V \)가 임의의 원소 \( u, v, w \), 스칼라 \( k, l \)에 대해 다음 8가지 조건을 모두 만족할 때, 공간 \( V \)를 벡터 공간 \( V \)라 하고, 벡터 공간 \( V \)의 원소를 벡터(vector)라고 부른다.
- ① \( (u + v) + w = u + (v + w) \)
- ② \( u + 0 = u \)를 만족하는 \( 0 \in V \)가 존재 (즉, 영 벡터(zero vector)가 \( V \) 안에 존재)
- ③ \( u + (-u) = 0 \)를 만족하는 \( -u \in V \)가 존재
- ④ \( u + v = v + u \)
- ⑤ \( k(u + v) = ku + kv \)
- ⑥ \( (k + l)u = ku + lu \)
- ⑦ \( (kl)u = k(lu) \)
- ⑧ \( 1 \cdot u = u \)
- 그리고 \( u + v \in V \)와 \( ku \in V \)라는 조건은 위의 조건들 중 기본적인 전제 조건으로 포함된다.
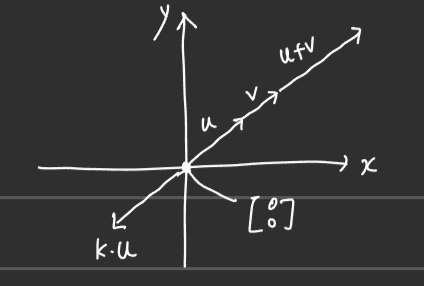
■ 예를 들어 벡터 공간 \( \mathbb{R}^2 \)는 \( xy \)평면 전체가 벡터 공간이 된다. \( \mathbb{R}^2 \)가 위의 조건들을 만족하는지에 대한 확인은 다음과 같다.

- \( xy \)평면 전체가 벡터 공간이므로 \( (0, 0) \) 성분을 가지는 영 벡터도 \( \mathbb{R}^2 \)에 속하기 때문에 조건 ②가 성립할 수 있다.
- 그리고 ①과 ③이 성립하는 이유는 전제 조건인 \( u + v \in V \)와 \( ku \in V \)가 \( \mathbb{R}^2 \)에서 성립하기 때문이다.
- ①과 ③은 벡터 공간 \( \mathbb{R}^2 \)에 존재하는 벡터들의 선형 결합이며, 이것을 의미하는 전제 조건이 \( u + v \in V \)이다.
- 이 전제 조건은 '벡터 공간에 존재하는 벡터들의 선형 결합의 결과도 벡터 공간에 존재하는가'이다.
- 실제로, 이 예에서 \( \mathbb{R}^2 \)에 존재하는 벡터 \( u, v, w \)의 선형 결합 \( 1 \cdot u + 1 \cdot v + 1 \cdot w \) 결과인 영 벡터가 \( \mathbb{R}^2 \)에도 존재하는 것을 볼 수 있다.
- 전제 조건 \( ku \in V \)가 의미하는 것은 '벡터 공간 \( V \)에 존재하는 벡터 \( u \)에 스칼라를 곱한 벡터 \( ku \)가 벡터 공간에 존재하는가'이다.
- 이 예에서 \( \mathbb{R}^2 \)에 존재하는 벡터 \( u \)에 스칼라 \( -1 \)을 곱한 \( -u \)가 \( \mathbb{R}^2 \)에 존재하는 것을 확인할 수 있다.
- 사실, 나머지 조건 ④부터 ⑧까지도 전제 조건 \( u + v \in V \)와 \( ku \in V \)와 관련된 것들이다.
■ 여기서 중요한 것은 벡터 공간이 되기 위해선 영 벡터(zero vector)가 벡터 공간에 존재해야 한다는 것이다.
- 예를 들어, 위의 \( \mathbb{R}^2 \)에서 \( (0, 0) \)이 존재하지 않는다고 가정하자. 그리고 벡터 \( u \)와 \( v \)가 다음과 같을 때, 두 벡터를 선형 결합하면

- 선형 결합의 결과가 영 벡터가 되지만, 영 벡터는 현재 가정에서 \( \mathbb{R}^2 \)에 속하지 않으므로 \( \mathbb{R}^2 \)는 벡터 공간이 될 수 없다.
■ 그러므로 벡터 공간인지 확인하기 위한 조건으로 어떤 집합이 '① \( u + v \in V \), ② \( ku \in V \), ③ 영 벡터(zero vector)가 존재' 이 3가지 조건만 만족한다면, 벡터 공간으로 볼 수 있다.
cf) 사실 위의 예에서 사용한 \( u = (1 0), v = (0 1) \)은 \( \mathbb{R}^2 \)의 '표준기저'이다. 즉, 이 두 벡터만 있으면 두 벡터의 선형 결합으로 \( \mathbb{R}^2 \)에 존재하는 모든 벡터들을 생성할 수 있다.
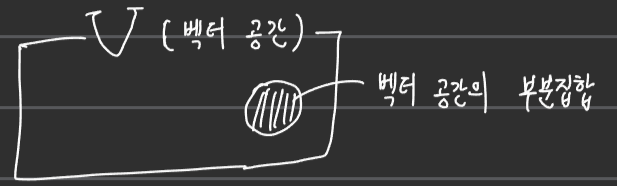
1.3 부분 공간(subspace)
■ 벡터 공간 \( V \)에 포함된 부분집합(subset) \( W \)가 다음 두 조건을 만족하면 부분공간 \( W \)라고 한다.
\( ① u, v \in W \Rightarrow u + v \in W \quad ② u \in W, k \in \mathbb{R} \Rightarrow ku \in W \)
■ 중요한 것은 부분 공간은 다음과 같이 벡터 공간의 일부(부분집합)이기 때문에 반드시 영 벡터(zero vector)가 존재해야 한다는 것이 전제 조건이 된다.
■ 그러므로 벡터 공간의 부분집합이 조건 \( ① u, v \in W \Rightarrow u + v \in W \quad ② u \in W, k \in \mathbb{R} \Rightarrow ku \in W \)과 ③ 영 벡터(zero vector)가 존재'를 만족하면, 이를 '부분 공간'이라고 할 수 있다.
- \( ① u, v \in W \Rightarrow u + v \in W \quad ② u \in W, k \in \mathbb{R} \Rightarrow ku \in W \)에서 조건 ①을 '덧셈에 대해 닫혀 있다', 조건 ②를 '스칼라 곱에 대해 닫혀 있다'고 표현한다.
■ 그리고 벡터 공간 \( V \)는 기본적으로 벡터 공간 정의를 만족하는 영 벡터와 자기 자신을 부분 공간으로 갖는다.
- 예를 들어, A = {0, 1, 2}라는 집합이 있을 때 A의 부분 집합은 공집합인 { }와 {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2} 그리고 자기 자신인 {0, 1, 2}가 된다.
■ 이 예를 \( \mathbb{R}^2 \)로 확장시켜 보자.
- 영 벡터 존재성을 포함하여 부분 공간을 만족하는 조건들을 나타내면 다음과 같다.
- ① 영 벡터가 부분 공간 \( W \)에 존재한다.: \( 0 \in W \)
- ② 덧셈에 대해 닫혀 있다.: \( u, v \in W \Rightarrow u + v \in W \)
- ③ 스칼라 곱에 대해 닫혀 있다. \( u \in W, k \in \mathbb{R} \Rightarrow ku \in W \)
■ \( \mathbb{R}^2 \)에서 위의 3가지 조건을 모두 만족하는 부분 공간은 다음과 같이 '원점을 지나가는 직선'밖에 존재하지 않는다.
■ 부분 공간이 되기 위해선 어떠한 스칼라를 곱하거나 같은 공간 내의 어떠한 벡터들을 더했을 때, 결과도 부분 공간 내에 존재해야 하기 때문이다. 영 벡터가 존재해야 하기 때문에 \( \mathbb{R}^2 \)에서는 위와 같이 \( u, v \)가 같은 직선 상에 존재해야 한다. 그래야 \( v = 0 \)이라고 했을 때 위의 조건 ②, ③을 모두 만족할 수 있다.
■ 만약, \( \mathbb{R}^2 \)의 부분 공간이 다음과 같이 1사분면이라고 가정해 보자. 1사분면 공간 내의 벡터들끼리 더했을 때, 그 결과도 1사분면 공간 내에 존재하므로 조건 ②를 만족한다.

■ 이렇게 공간 내에서 공간에 속하는 벡터를 더했을 때, 그 결과도 공간 내에 존재하는 것을 조건 ② '덧셈 연산에 대해 닫혀 있다.'라고 한다.
■ 이 예시는 조건 ②는 만족하나 조건 ③을 만족하지 않는다. 1사분면에 존재하는 임의의 벡터에 스칼라 \( - 1\)을 곱하면, 곱해진 벡터는 더 이상 1사분면이라는 공간에 존재하지 않기 때문이다.

■ 이런 상황을 ' 스칼라 곱에 대해 닫혀 있지 않다.'라고 말하며, 반대로 \( 2v \) 같이 공간 내에 존재하면, 이를 조건 ③ '스칼라 곱에 대해 닫혀 있다.'라고 한다.

- 그러므로 \( \mathbb{R}^2 \)에서 1사분면은 벡터 공간이 될 수 없다. 그리고 애초에 벡터 공간이 아니므로 \( \mathbb{R}^2 \)의 부분 공간이라고 정의할 수도 없다.
■ 이 예를 조금만 바꿔 보면 영 벡터 공간 {0}이 벡터 공간의 부분 공간임을 알 수 있다.
- 그 이유는 {0}은 당연히 영 벡터를 포함하고, 덧셈에 대해 닫혀 있다. ( \( 0 + 0 = 0, u + 0 = u, v + 0 = v \) )
- 그리고 스칼로 곱에 대해서도 닫혀 있다. ( \( k \cdot 0 = 0 \) )
- 이러한 원리는 모든 차원에 적용된다. 그러므로 {0}은 모든 벡터 공간의 부분 공간이 된다.
- 그리고 벡터 공간 \( V \)의 자기 자신도 부분 공간이 되는 이유도 벡터 공간 \( V \) 자체가 영 벡터를 포함하고 벡터 덧셈과 스칼라 곱에 대해 닫혀 있기 때문이다.
■ 정리하면, 벡터 공간 \( \mathbb{R}^n \)은 {0}과 자기 자신 \( \mathbb{R}^n \)을 부분 공간으로 갖는다.
■ 이렇게 \( \mathbb{R}^2 \)의 부분 공간은
- (1) {0} (zero vector)
- (2) 원점을 지나가는 직선
- (3) \( \mathbb{R}^2 \) (자기 자신. 즉, xy평면 전체)가 된다.
■ \( \mathbb{R}^3 \)의 부분 공간은 \( \mathbb{R}^2 \)의 부분 공간에 원점을 지나가는 평면이 포함된다. \( \mathbb{R}^3 \)도 기본적으로 {0}과 자기 자신을 부분 공간으로 갖으며, \( \mathbb{R}^2 \)의 상위 차원이므로 원점을 지나가는 직선도 포함되어 있다.
■ 그리고 \( \mathbb{R}^2 \)에서 원점을 지나가는 직선을 부분 공간으로 갖는 이유와 동일한 이유로 다음과 같이 원점을 지나가는 평면을 부분 공간으로 갖는다.
- 정확하게는 평면 안의 두 벡터를 더하면 그 합은 여전히 평만 안에 존재한다.
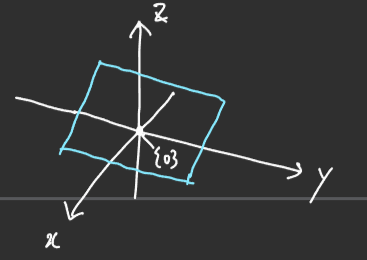
■ 정리하면, \( \mathbb{R}^3 \)의 부분 공간은
- (1) {0} (zero vector)
- (2) 원점을 지나가는 직선
- (3) 원점을 지나가는 평면
- (3) \( \mathbb{R}^3 \)
■ \( \mathbb{R}^2 \)와 \( \mathbb{R}^3 \)의 부분 공간 예시로 알 수 있는 것은 임의의 벡터 공간 \( V \)가 존재할 때, 벡터 공간 \( V \)는 ' {0}을 제외하고도' 서로 다른 두 개의 부분 공간을 갖는다는 사실이다.
1.3.1 부분 공간의 연산
■ 어떤 집합 \( X \)의 두 부분집합 \( A, B \)가 있다면, 두 부분집합의 교집합과 합집합을 통해 새로운 부분집합을 만들 수 있다.
■ 벡터 공간 \( V \)의 두 부분 공간 \( W_1, W_2 \)도 기본적으로 집합 \( V \)의 부분집합이므로 교집합 \( W_1 \cap W_2 \), 합집합 \( W_1 \cup W_2 \)을 만들 수 있다.
■ \( W_1 \cap W_2 \)과 \( W_1 \cup W_2 \)도 다시 부분 공간이 될 수 있는지 확인해 보자.
■ 예를 들어 \( \mathbb{R}^3 \)에서 원점을 지나는 서로 다른 두 평면이 있다고 했을 때, '원점을 지나는 평면'이므로 두 평면은 2차원 부분 공간이다.
- 이때 두 부분 공간을 \( W_1, W_2 \)라고 했을 때, \( W_1 \)과 \( W_2 \)의 교집합은 두 평면의 교선이며, 이 또한 원점을 지나므로 \( \mathbb{R}^3 \)의 부분 공간이 된다.
- 반면, 각 부분 공간에서 교선 위에 있지 않은 벡터 \( w_1 \in W_1, w_2 \in W_2 \)를 하나씩 선택하여 더하면 \( w_1 +w_1 \)는 \( W_1 \)에 속하지 않고 \( W_2 \)에도 속하지 않으므로 \( W_1 \cup W_2 \)에 속하지 않는다.
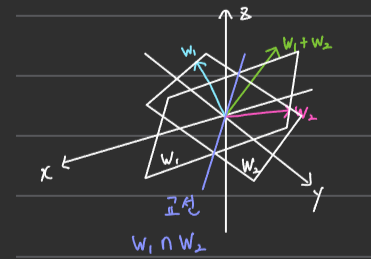
- 그러므로 \( W_1 \cup W_2 \)는 벡터 공간이 아니다.
■ \( V \)의 두 부분 공간 \( W_1, W_2 \)를 모두 포함하는 부분 공간은 임의의 두 벡터 \( w_1 \in W_1, w_2 \in W_2 \)를 더한 벡터 \( w_1 + w_2 \)를 모두 포함하고 있어야 한다.
■ 즉,두 벡터 공간을 모두 포함하는 벡터 공간 \( W_1 + W_2 \)를
\( W_1 + W_1 := {w_1 + w_2 : w_1 \in W_1, w_w \in W_2 } ⊂ V \)로 정의할 수 있다.
■ \( W_1 + W_2 \)의 임의의 두 원소 \( a_1, a_2 \)가 \( a_1 = u_1 + u_2 \), \( a_2 = w_1 + w_2 \)이라고 할 때, \( u_1, w_1 \in W_1 \), \( u_2, w_2 \in W_2 \)
■ 벡터 공간 \( V \)에서 덧셈에 대한 교환 법칙, 결합 법칙이 성립한다는 성질과 \( W_1, W_2 \)가 각각 부분 공간이라는 것을 이용하면 \( a_1 + a_2 \)가 \( W_1 + W_2 \)에 속하는 것을 확인할 수 있다.
\( a_1 + a_2 = (u_1 + u_2) + (w_1 + w_2) = (u_1 + w_1) + (u_2 + w_2) \in W_1 + W_2 \)
■ 비슷한 방법으로 임의의 스칼라 \( k \)에 대해 \( k \cdot a_1 \in W_1 + W_2 \)를 확인할 수 있다.
- 스칼라는 벡터의 길이에만 영향을 주므로 \( a_1 = u_1 + u_2, \quad k \cdot a_1 = k(u_1 + u_2) \in W_1 + W_2 \)
■ 결과적으로 \( W_1 + W_2 \)와 \( W_1 \cap W_2 \)는 \( V \)의 부분 공간이 된다.
- 항상 주의할 것은 \( W_1 + W_2 \)가 의미하는 것이 합집합이 아니다라는 것과
- \( W_1 \cap W_2 \)가 \( W_1 \)의 기저와 \( W_2 \)의 기저의 교집합이 아니라는 점. \( W_1 \cap W_2 \)는 원점을 지나가는 하나의 교선이라는 점. 즉 \( W_1 \)과 \( W_2 \) 두 부분 공간의 조건을 \( W_1 \cap W_2 \)가 모두 만족해야 하는 개념이라는 점이다.
■ 예를 들어, 다음과 같은 두 개의 부분 공간이 존재한다고 할 때, \( W_1 \cap W_2 \)

- \( x_2, x_3 \)는 \( x_1 \)에 의해 결정된다. 그러므로 위의 조건에서 자유롭게 선택 가능한 변수는 \( x_1, x_4 \)이다. 즉, 독립적인 변수 \( x_1\)과 \( x_4 \)를 중심으로 2개의 기저 벡터를 생성할 수 있다.
- 예를 들어, \( x_1 = 1 \)이면, \( x_2 = \frac{1}{2}, x_3 = 3 \)이 되고, \( x_4 = 0 \)으로 설정하면 된다. 다른 하나의 기저는 \( x_4 = 1 \)로 설정하고 \( x_1 = 0 \)으로 설정하면 된다.
- 그러면 기저는 \( W_1 \cap W_2 \) \( {(1, \frac{1}{2}, 3, 0), (0, 0, 0, 1)} \) 2개이므로 차원은 2차원이다.
■ 가우스 조던 소거법을 이용해 기저를 구할 수 있다. 예를 들어, \( \mathbb{R}^4 \)의 두 부분 공간 \(W_1, W_2 \)가 다음과 같을 때,

- 주어진 벡터를 행으로 갖는 행렬의 기약 행사다리꼴을 구하면

- 각 부분 공간을 생성하는 벡터들은 각각 선형 독립이고 기저가 된다. 그리고 부분 공간의 차원은 \( \mathbb{R} \)에서 \( \text{dim} (W_1) = \text{dim} (W_2) = 3 \)이다.
- 기약 행사다리꼴의 각 행벡터들도 각 부분 공간의 기저를 이룬다.
- 위의 기약 행사다리꼴로부터 구한 \( W_1 \)의 기저 \( {(1, 0, 0, 1), (0, 1, 0, 0), (0, 0, 1, 0)} \)와 \( W_2 \)의 기저 \( {(1, 0, 0, 1), (0, 1, 0 , 0), (0, 0, 1, -1) } \) 중 (1, 0, 0, 1)과 (0, 1, 0, 0)은 두 부분 공간에 동시에 속하는 선형 독립인 벡터이다.
- 즉, \( W_1 \cap W_2 \)의 기저가 (1, 0, 0, 1)과 (0, 1, 0, 0)이며, 기저가 2개이므로 \( W_1 \cap W_2 \)의 차원은 2차원이라는 것을 알 수 있다.
- 포함 관계를 나타내면,
\( {(1, 0, 0, 1), (0, 1, 0, 0)} \) ⊂ \( W_1 \cap W_2 \) ⊂ \( W_1 \) = \( {(1, 0, 0, 1), (0, 1, 0, 0), (0, 0, 1, 0)} \)
- \( W_1 + W_2 \)의 기저는 \( {(1, 0, 0, 1), (0, 1, 0, 0), (0, 0, 1, 0), (0, 0, 1, -1)} \)이므로 4차원이다
- \( \text{dim} (W_1) = \text{dim} (W_2) = 3 \), \( \text{dim}(W_1 \cap W_2) = 2 \), \( \text{dim}(W_1 + W_2) = 4 \)
■ 이 결과로부터 실수 상에서 정의된 벡터 공간 \( V \)의 두 부분 공간 \( W_1, W_2 \)에 대하여 \( \text{dim} (W_1 + W_2) = \text{dim} (W_1) + \text{dim} (W_2) - \text{dim} (W_1 \cap W_2) \)가 성립함을 알 수 있다.
1.4 벡터 공간 생성(span)
■ 벡터 공간 개념을 기반으로 선형(일차) 결합을 설명하면, 선형 결합은 '벡터 공간 \( V \)의 원소(성분)' \( v_1, v_2, \cdots, v_n \)이고 임의의 실수 \( a_1, a_2, \cdots, a_n \)가 존재할 때, \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n \)이다.
■ 즉, 벡터 공간 \( V \)의 원소 \( v_1, v_2, \cdots, v_n \)이 벡터 공간 \( V \)를 생성(span)한다고 볼 수 있다.
- 이를 \( <v_1, v_2, \cdots, v_n> = \text{span} \left\{ v_1, v_2, \cdots, v_n \right\} = a_1 v_1 + a_2 v_2 + \cdots + a_n + v_n = V \)로 표현할 수 있다.
- 이렇게 선형 결합을 통해 만드는 과정을 '생성시켰다'라고 한다.
■ 예를 들어 \( \mathbb{R}^2 \)에서 열벡터 (1 0)과 (0 1)이 다음과 같이 선형 결합으로 다른 벡터들을 생성시킬 수 있다.

- 이 예에서 (1 0)과 (0 1)은 표준 기저이므로 두 벡터로 생성되는 공간은 \( \mathbb{R}^2 \)가 된다. \( a(1 0) + b(0 1) = \mathbb{R}^2 \)
1.5 선형(일차) 독립(linear independent)과 선형 종속(linear dependent)
■ 벡터 공간 V(\( \mathbb{R}^n \))의 부분집합 \( {v_1, v_2, \cdots, v_n} \)과 임의의 실수 \( a_1, a_1, \cdots, a_n \)에 대해 선형 결합 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0 \)이라 할 때,
- ① \( a_1 = a_2 = \cdots = a_n = 0 \)이면 \( {v_1, v_2, \cdots, v_n} \)은 선형 독립이라 하고
- ② \( a_1, a_2, \cdots , a_n \) 중에 적어도 하나 0이 아닌 것이 존재하면, \( {v_1, v_2, \cdots, v_n} \)은 선형 종속이라고 한다.
- ②를 다른 말로 표현하면, \( a_1, a_2, \cdots , a_n \) 중에 0이 아닌 수를 벡터에 곱해서 결과를 0으로 만들 수 있다면 선형 종속이다.
■ ①의 상황에서는 자명해(trivial solution)를 갖는다. 그 이유는 다음과 같이 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0 \)에서 상황을 나타내면 다음과 같다.

■ 이런 경우에는 좌변이 0이 되려면 \( {v_1, v_2, \cdots, v_n} \)이 모두 0이 아닌 이상 \( a_1 = a_2 = \cdots = a_n = 0 \)이 되어야 한다.
■ 예를 들어 \( \mathbb{R}^2 \), \( \mathbb{R}^3 \)에서 다음과 같이 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0 \)이라 할 때,

유일하게 가능한 해는 0밖에 없다. 그러므로 자명한 해를 갖는다고 하는 것이다.
■ 이렇게 \( Av = 0 \), \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0 \)처럼 '0'을 만드는데 있어서 가능한 \( a_1 = a_2 = \cdots = a_n \)이 '0' 밖에 없다면 \( v_1, v_2, \cdots, v_n \)은 독립 관계이다.
- 위의 \( \mathbb{R}^2 \) 예시에서는 \( v_1 \)과 \( v_2 \)는 독립 관계이고, \( \mathbb{R}^3 \) 예시에서는 \( v_1 \)과 \( v_2 \) 그리고 \( v_3 \)은 독립 관계이다.
■ 이와는 반대로 선형 종속 ②의 상황은 비자명해(non-trivial solution)가 존재한다. 이는 선형 종속인 경우, 자명한 해 0을 갖지 않더라도 선형 결합 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n \)의 결과를 0으로 만들 수 있기 때문이다.
■ 예를 들어 \( \mathbb{R}^2 \), \( \mathbb{R}^3 \)에서 다음과 같이 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n = 0 \)이라 할 때,

■ 위의 선형 종속 예시와 같이 하나 혹은 두개 혹은 나머지 벡터에다 적당한 실수배를 하고 덧셈 또는 뺄셈을 해서 만들 수 있다면 '불필요한 존재가 있다'라고 얘기하며, 이를 종속이라고 한다.
- 이 내용을 공간 상에서 보면 종속인 벡터는 서로 평행하다는 것이다. 위의 \( \mathbb{R}^2 \)의 예를 보면 알 수 있다.
■ 다시 말해, 적당한 실수배로 더하고 빼서 다른 원소를 만들어 낼 수 있으면 '속해 있다.' 즉, 종속이라고 얘기한다. 이 개념을 행렬에 적용할 수 있다.
■ \( Ax = b \)에서 가우스 (조던) 소거법은 적당한 실수배로 더하고 빼는 과정을 진행한다.
- 이때, 한 행이라도 모든 원소가 '0'이 된다면, 이는 다른 행과 '종속'인 상황이라고 볼 수 있다.
- 반대로 한 행이라도 모든 원소가 '0'이 되지 않는다면, '독립'인 상황이라고 볼 수 있다.
■ 예를 들어, 다음과 같은 벡터들을 기약 행사다리꼴로 만들었을 때, 벡터들의 관계가 종속임을 알 수 있다.

- (2 3)이었던 자리가 (0 0)이 나온다는 것은 (1 0)과 (0 1)로 (2 3)을 제거할 수 있다.는 것이다.
- 즉, 반대로 생각하면 (1 0)과 (0 1)로 (2 3)을 생성할 수 있다.라는 얘기이다. 그러므로 종속이다.
■ 반대로 다음과 같은 벡터들은 독립임을 알 수 있다.

- 이는 \( v_1 \)과 \( v_2 \)를 이용해서 \( v_3 \)를, \( v_2 \)와 \( v_3 \)를 이용해서 \( v_1 \)을, \( v_1 \)과 \( v_3 \)을 이용해서 \( v_2 \)를 생성할 수 없다는 의미이다.
■ 그러므로 이 내용을 '행렬식'에 적용하면, 선형 독립인 경우 행렬식 값은 0이 아니고, 선형 종식인 경우 행렬식 값은 0이 된다는 것을 알 수 있다.
- 행렬식에서 한 행(또는 열)의 모든 원소가 0이라면 행렬식 값은 0이 되기 때문이다.

2. 벡터 공간에서 기저(basis)와 차원(dimension)
2.1 벡터 공간에서 기저에 대한 정의
■ 벡터 공간 \( V \)에 대하여 \( S = \left\{ v_1, v_2, \cdots, v_n \right\} \)를 \( V \)의 부분집합이라고 하자. 이때 집합 \( S \)가 다음 두 가지 조건을 만족할 때, \( S \)를 \( V \)의 기저라고 한다.
① \( {v_1, v_2, \cdots, v_n} \)이 \( V \)를 생성한다. ② \( {v_1, v_2, \cdots, v_n} \)이 선형 독립이다.
- 기본적인 조건은 벡터 공간 \( V \)의 부분집합 \( S \)의 원소의 개수가 유한개여야 한다.
■ 다시 말해, ① \( {v_1, v_2, \cdots, v_n} \)이 \( V \)를 생성한다. ② \( {v_1, v_2, \cdots, v_n} \)이 선형 독립이다. 라는 조건은 집합 \( {v_1, v_2, \cdots, v_n} \)이 공간을 생성하고 독립이면 \( S = \left\{ v_1, v_2, \cdots, v_n \right\} \)를 벡터 공간 \( V \)의 '기저'라고 한다.
■ 예를 들어 \( \mathbb{R}^2 \)와 \( \mathbb{R}^3 \)의 기저는 다음과 같다.


- 표준 기저의 형태는 한 성분만 1이고 나머지는 모두 0인 벡터로, 같은 공간 내의 모든 벡터는 표준 기저 벡터들의 선형 결합으로 표현될 수 있다.
- \( \mathbb{R}^2 \)의 기저 개수는 2개, \( \mathbb{R}^3 \)의 기저 개수는 3개, \( \mathbb{R}^4 \)의 기저 개수는 4개, .... , \( \mathbb{R}^n \)의 기저 개수는 \( n \)개가 된다.
■ 이때, 각 차원에서 기저가 변동될 수는 있어도, '기저의 개수 = 차원'이므로 기저의 개수는 변하지 않는다.
■ 즉, \( S = \{v_1, v_2, \cdots, v_n\} \)가 벡터 공간 \( V \)의 기저이면,
\( S \)의 원소의 개수 \( n \) ( 기저의 개수 \( n \)개 ) \( \Leftrightarrow \) 벡터 공간 \( V \)의 차원 ( \( \text{dim} (V) = n \) )
2.2 기저에 대한 좌표 벡터와 좌표 공간으로의 변환
■ \( S = \left\{ \mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_n \right\} \)이 벡터 공간 \( V \)의 기저라고 했을 때, \( V \)에 속하는 모든 벡터 \( v \)는 적당한 실수 \( a_1, a_2, \cdots, a_n \)에 대하여 선형 결합 \( a_1 v_1 + a_2 v_2 + \cdots + a_n v_n \)으로 나타낼 수 있다.
■ 이때, 선형 결합의 계수 \( a_1, a_2, \cdots, a_n \)로 나타낸 결과가 벡터 \( v \)의 좌표 벡터이다.
■ 좌표 벡터는 보통 \( [v]_S = (a_1, a_2, \cdots, a_n) \)으로 표현하며, 기저 \( S \)에 대한 \( v \)의 좌표 벡터(상대 벡터, 좌표 행렬)이라고 한다.
■ 예를 들어, 어떤 벡터 공간의 기저를 \( {v_1, v_2, v_3} \)이라고 했을 때, 선형 결합으로 \( a_1 v_1 + a_2 v_2 + a_3 v_3 = w \)로 어떤 \( w \)라는 벡터를 만들었다고 하자. 이때의 선형 결합 계수들을 다음과 같이 나타낸 걸 '좌표(벡터, 행렬, 혹은 행렬 좌표)'라고 한다.

■ 그리고 벡터 공간은 기저에 의해 좌표 공간으로 변환될 수 있다. 예를 들어 다음과 같이 벡터 공간 \( V \)의 기저 \( \alpha, \beta, \gamma \)가 존재한다면,
기저가 조금씩 바뀔때 마다 \( \alpha, \beta, \gamma \)가 벡터 공간 \( V \)를 생성할 때 나오는 좌표들이 있을 것이다. 생성할 때 나오는 좌표들을 다 모아 놓은 것을 '좌표 공간'이라 한다.
■ 예를 들어 \( \mathbb{R}^2 \)에서 표준 기저 { (1 0), (0 1) }과 (일반) 기저 { (1 0), (1 1) }을 각각 선형 결합하여 벡터 (2 3)을 만들었다고 하자.

- 이렇게 기저를 통해 벡터 공간에서 좌표 공간으로 변환할 수 있다.
3. 내적 공간
■ 임의의 벡터 공간 \( V \)의 두 벡터 \( u, v \)에 대해 실수 \( u \cdot v \)를 대응시키는 연산 \( \cdot \)이 다음 성질을 만족할 때, 연산 \( \cdot \)을 '내적'이라 부르고 \( V \)를 내적 공간이라고 한다.
- \( u, v, w \)는 \( V \)에 속하는 임의의 벡터이고, \( c \)는 임의의 스칼라일 때,
- 내적 규칙 ① \( u \cdot u \geq 0 \)이며, 이 등식이 성립할 필요충분조건은 \( u = 0 \)이다. ( \( u = 0 \)일 때만 성립한다. )
- 내적 규칙 ② \( u \cdot (v + w) = u \cdot v + u \cdot w \), \( (u + v) \cdot w = u \cdot w + v \cdot w \)
- 내적 규칙 ③ \( u \cdot (cv) = c(u \cdot v) \), \( (cu) \cdot v = c(u \cdot v) \)
- 내적 규칙 ④ \( u \cdot v = v \cdot u \)
■ 내적 규칙 ①은 벡터가 자기 자신과의 내적이 0이라면, 그 벡터는 오직 영 벡터(zero vector)일 때. 라는 조건이다. 이는 벡터의 길이(norm)를 \( \sqrt{u \cdot u} \)로 정의했을 때, 길이가 0인 벡터는 영벡터뿐이라는 말과 같다.
- 또한, ① \( u \cdot u \geq 0 \)는 길이는 음수가 될 수 없다.라는 것을 의미한다.
■ 내적 규칙 ①은 \( \mathbb{R}^n \)에서 두 벡터 \( a = (a_1, a_2, \cdots, a_n) \), \( b = (b_1, b_2, \cdots, b_n) \)에 대하여
\( <a, b> = a_1 b_1 + a_2 + b_2 + \cdots + a_n b_n = \sum\limits_{i=1}^{n} a_i b_i \)
- 이때 \( <a, a> = \sum\limits_{i=1}^{n} a^2_i \geq 0 \)이고 \(a^2_i = 0 \)일 필요충분조건은 \( a_i = 0 \)이므로 내적 규칙 ①이 성립한다.
cf) \( <a, b> = a_1 b_1 + a_2 + b_2 + \cdots + a_n b_n = \sum\limits_{i=1}^{n} a_i b_i \)와 같이 정의된 내적을 \( \mathbb{R}^n \)의 '유클리드 내적'이라 부른다.
■ 내적 규칙 ②는 분배 법칙, 내적 규칙 ③은 스칼라 곱에 대한 호환성 - 한 벡터에 스칼라를 곱한 뒤 내적을 취하는 것과 내적의 결과에 스칼라를 곱하는 것은 동일하다. 내적 규칙 ④는 대칭성으로 두 벡터를 내적했을 때 순서를 바꾸어도 결과가 같다는 성질이다.
■ 내적 공간 \( V \)에서 벡터 \( u \)의 크기 \( || u || \)를 \( || u || = \sqrt{<u, u>} \)와 같이 정의하고, 이 크기(길이)를 주는 함수 \( || || \)를 벡터의 '노름(norm)'이라고 부른다.
- 예를 들어, 내적 공간 \( \mathbb{R}^2 \)에서 각 벡터의 크기는 \( || a || = \sqrt{<a, a>} = \sqrt{a \cdot a} \)이다.
'선형대수' 카테고리의 다른 글
| [개념] 행렬의 기본 공간과 차원 정리 (0) | 2025.01.22 |
|---|---|
| Spaces of Vectors - (2) Column Space and Nullspace (0) | 2025.01.21 |
| Spaces of Vectors - (1) Vector Spaces and Subspaces (0) | 2025.01.20 |
| Solving Linear Equations - (4) Inverse Matrices, (5) Elimination = Factorization: A = LU, (6) Permutations (0) | 2025.01.18 |
| [개념] 행렬 (3) (0) | 2025.01.18 |



