1. Inverse Matrices
■ 정방행렬 \( A \)가 있을 때, 이 행렬의 역행렬이 존재할 수도, 존재하지 않을 수도 있다. 모든 행렬에 역행렬이 있는 것은 아니기 때문이다.
■ 만약, 정방행렬 \( A \)의 역행렬이 존재한다면, \( AA^{-1} = I = A^{-1}A \)이 성립하며, 이때의 \( A \)는 가역행렬 또는 정칙행렬이라 하고, \( A^{-1} \)는 \( A \)의 역행렬이라 한다.
- 중요한 것은, \( A \)의 역행렬이 존재한다는 조건이 붙을 때, 위의 식이 성립한다는 것이다.
■ 가역행렬 또는 정칙행렬은 역행렬이 존재하는 행렬(invertible matrix)을 의미하며, invertible이면 nonsingular matrix. 해가 존재하는 행렬이다.
■ 행렬이 주어졌을 때, 역행렬 존재 여부를 확인하는 일반적인 방법은 가역행렬의 행렬식 값을 확인하는 방법이다.
- 가역행렬의 행렬식 값 \( \text{det} (A) \)값이 0 \( \Leftrightarrow \) \( A \)는 비가역행렬이다. (=정칙행렬이 아니다.)
- 반대로, 가역행렬의 행렬식 값 \( \text{det} (A) \)값이 0이 아니면 \( \Leftrightarrow \) \( A \)는 가역행렬이다. (=정칙행렬이다.)
■ \( \det(A) = 0 \Leftrightarrow A \text{는 비가역행렬이다.} \)가 성립하는 이유는 다음과 같다.
- 예를 들어, 다음과 같은 행렬 \( A \)가 있을 때, \( A \)와 같은 크기를 가지는 \( A \)의 역행렬 \( B \)가 존재한다고 하자.

- \( A \)의 역행렬 \( B \)가 존재한다면, 다음과 같이 \( AB = I \)가 성립해야 한다.

- 행렬의 곱셈 \( AB \)를 \( A \)의 열벡터들의 일차(선형)결합으로 보자.
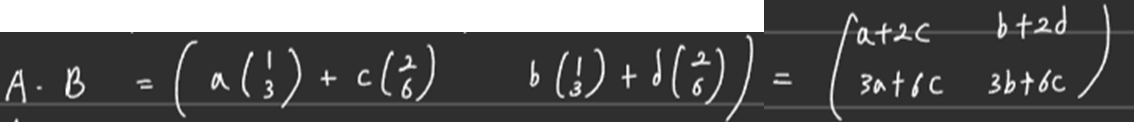
- 여기서, \( AB \)의 첫 번째 열벡터는 \( 2 \times 2 \) 크기를 가지는 단위행렬의 첫 번째 열벡터와 동일해야 하다.

- 다시 말해, 행렬 \( A \)의 열벡터들의 선형 결합으로 [ 1 0 ]을 만들어야 한다. 하지만 이는 불가능하다.
- 그 이유는 다음과 같이 \( A \)의 열벡터들이 같은 방향이기 때문이다.

- 이런 상황을 연립일차방정식에서는 두 직선이 평행하다. 또는 해가 존재하지 않는다고 하였다.
https://hyeon-jae.tistory.com/166
Solving Linear Equations - (2) The Idea of Elimination, (3) Elimination Using Matrices
1. The Idea of Elimination1.1 Two Equations in Two Unknowns■ 선형 방정식을 해결하는 체계적인 방법은 '소거법(elimination)'이다. ■ 첫 번째 방정식에 3을 곱해 \( 3x - 6y = 3 \)으로 만든 후, 두 번째 방정식에서
hyeon-jae.tistory.com
■ 이러한 비가역행렬의 특징을 보면, 두 개의 행(또는 열)이 비례 관계임을 알 수 있다. 이런 경우 행렬 \( A \)의 행렬식 값 \( \det(A) = 0 \)이 되기 때문에 \( \det(A) = 0 \Leftrightarrow A \text{는 비가역행렬이다.} \)가 성립하는 것이다.
- 또한, 이런 행렬을 행의 관점(row picture)에서 봤을 때, 두 개의 연립일차방정식은 평행한 것을 알 수 있다.
- 다시 말해, 두 개의 행이 비례 관계라면, 두 연립일차방정식은 평행하다는 것을 알 수 있다.
■ 행렬식으로 역행렬을 판별하는 방법 외에 \( Ax = 0 \)을 이용하여 판별하는 방법이 있다.
- 예를 들어 \( A \) 행렬에 다음과 같은 열벡터를 곱하면 \( Ax = 0 \)이 된다. 결론부터 말하자면, \( Ax = 0 \)이 성립한다면, \( A \)는 비가역행렬이자 해가 존재하지 않는 행렬이다.

- 중요한 것은 \( x \neq 0 \)이라는 것이다.
- 그러나, \( Ax = 0 \)에 \( A^{-1} \)이 존재한다는 가정 하에, \( A^{-1} \)을 왼쪽에 곱하면, \( x = 0 \)이 되는 것으로 나온다.
1.1 Calculating \( A^{-1} \) by Gauss-Jordan Elimination
■ 역행렬을 구하는 방법 중 가우스 조르단 소거법을 이용하여 구하는 방법이 있다.
■ 이 방법의 기본 아이디어는 단위행렬을 이용하는 것이다.
■ 더 자세하게 말하면, \( n \times n \) 행렬 \( A \)에 대해 \( A^{-1}A = I \)를 만족하는 행렬 \( A^{-1} \)이 존재하면 \( AA^{-1} = I \)도 성립하고, \( A^{-1} \)이 \( A \)의 역행렬이 됨을 알 수 있다.
■ 그러므로, 행렬의 곱을 열벡터의 일차결합으로 보는 방식을 이용하면, 행렬 \( A \)의 역행렬 \( A^{-1} \)을 구하는 것은 다음 \( n \)개의 연립방정식을 푸는 것과 같다.
- \( A \)의 역행렬을 \( X \)라고 하자.
\( AX_1^C = I_1^C, AX_2^C = I_2^C, \cdots, AX_n^C = I_n^C \)
- \( I_j^C \)는 \( i \)번째 성분만 1이고, 나머지는 모두 0인 열벡터를,
- \( X_i^C \)는 각각 \( n \)개의 미지수로 이뤄진 열벡터를 의미한다.
■ 예를 들어, 다음과 같은 행렬 \( A \)가 있다고 할 때, \( A \)의 역행렬이 존재하면 \( AA^{-1} = I \)가 될 것이다.
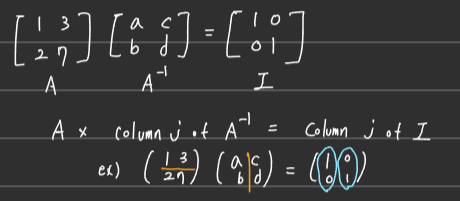
■ Gauss-Jordan 방법의 원리 \( AX_1^C = I_1^C, AX_2^C = I_2^C, \cdots, AX_n^C = I_n^C \)는 다음과 같이 두 개의 방정식을 동시에 해결한다.

■ 이런 연립방정식 \( AX_i^C = I_i^C \)를 푸는 가장 간단한 방법은 확대행렬 \( (A \mid I_i^C \)에 Gauss-Jordan 소거법(Elimination)을 적용시켜 (기본 행연산을 이용해) 기약 행사다리꼴을 만드는 것이고, 행렬 \( A \)가 역행렬을 갖는 경우에는 그 결과가 \( (I \mid B_i) \) 꼴이 되어 \( X_i^C = B_i \)와 같이 해를 구하게 된다.

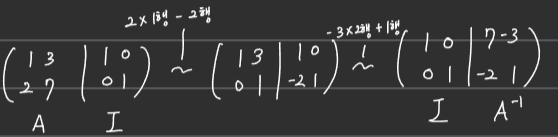
- \( (A \mid I) \)에서 시작한 확대행렬이 \( (I \mid A^{-1} \)로 끝나는 것을 볼 수 있다.
- 즉, Gauss-Jordan 소거법을 이용한 방법은 \( A^{-1}A = I \)가 되는 것을 반대로 생각하여 \( A^{-1} \)을 계산하는 것이다.
- 위의 Gauss-Jordan 소거법을 이용한 역행렬을 구하는 과정에서 중요한 것은 기본 행연산을 어떻게 적용시킬지는 오직 행렬 \( A \)에 의해서만 결정된다는 점이다.
2. Elimination = Factorization: A = LU
■ 소거(elimination)는 행렬에서 값(해)를 찾는 올바른 방법이다.
■ \( A = LU \)같은 분해는 가장 기본적인 행렬의 인수분해로, 이 역시 복잡한 형태의 형태를 단순화시켜 해를 구하기 위함이다.
■ Elimination Using Matrices에서 연립방정식의 해를 구하고자, 연립방정식을 행렬로 바꾼 다음, 행렬 \( A \)에 소거법을 적용시켜 대각선에 pivot이 있는 상삼각행렬 \( U \)로 단순화하여 해를 구할 수 있었다.
https://hyeon-jae.tistory.com/166
Solving Linear Equations - (2) The Idea of Elimination, (3) Elimination Using Matrices
1. The Idea of Elimination1.1 Two Equations in Two Unknowns■ 선형 방정식을 해결하는 체계적인 방법은 '소거법(elimination)'이다. ■ 첫 번째 방정식에 3을 곱해 \( 3x - 6y = 3 \)으로 만든 후, 두 번째 방정식에서
hyeon-jae.tistory.com
■ 여기서 \( A \)에서 \( U \)로 가기 위한 연결 고리는 '소거를 한 번에 처리하는 행렬'이었다.
■ \( A = LU \)는 이와 반대로 \( A \)와 \( U \) 사이에, 이 둘을 연결하는 하삼각행렬 \( L \)을 통해 어떤 연립방정식을 \( L \)과 \( U \)로 분해하여 해를 구하는 방법이다.
■ 여기서 \( L \)이 무엇이 되는지를 잘 설명할 수 있는 예시가 역행렬이다.
- 예를 들어, 어떤 행렬 \( A \)를 단위행렬 \( I \)로 만들고자 하면, 필요한 연결 고리는 \( A^{-1} \)이다. \( AA^{-1} = I \)
- 혹은 행렬곱 \( AB \)를 단위행렬 \( I \)로 만들고자 하면, 필요한 연결 고리는 \( B^{-1}A^{-1} \)이다.
- \( AB \)에 \( (AB)^{-1} = B^{-1}A^{-1} \)을 순서대로 곱해 단위행렬을 만드는 이유는 행렬의 곱셈에서는 일반적으로 \( AB \neq BA \)이며, 결합법칙 \( (AB)C = A(BC) \)가 성립하기 때문이다.
■ 즉, 어떤 행렬 \( A \)에 소거법을 적용시켜 \( (E_{32}E_{31}E_{21})A = U \) 연립방정식의 해를 나타내는 pivot이 있는 상삼각행렬 \( U \)를 만들었다고 하자.
■ 여기서 소거행렬 \( (E_{32}E_{31}E_{21}) \)의 역행렬인 \( E^{-1}_{21}E^{-1}_{31}E^{-1}_{32} \)가 \( A \)와 \( U \)를 연결하는 하삼각행렬 \( L \)이 되는 것이다.
■ 예를 들어 다음과 같이 \( E_21A = U \)가 있다면, \( A = E^{-1}_{21}U \)가 되며, 여기서 \( E^{-1}_{21} \)이 \( L \)이 된다.

■ 여기서 \( E \)의 역할을 생각해 본다면, 하삼각행렬 \( L \)에는 가우스 소거법의 승수(multiplier)를 저장한다는 것을 알 수 있다. 즉, \( L \)은 소거 과정을 저장하는 역할을 한다.
■ 그리고 상삼각행렬 \( U \)는 pivot 값을 저장한다. 다른 말로 \( U \)는 소거 과정의 결과를 저장하는 역할을 한다.
■ 이를 다른 관점에서 보면, \( L \)과 \( U \)에 행렬 \( A \)에 대한 모든 정보가 나뉘어 저장되어 있는 것으로 볼 수 있다.
■ 만약, pivot들만 따로 분리하여 행렬을 만들고 싶을 때는 pivot들을 포함하는 대각행렬 \( D \)로 \( U \)를 나누어 \( A = LDU \)로 나타내면 된다.
■ \( D \)는 대각 원소가 pivot이고 나머지는 모두 0인 대각행렬(pivot만 저장하는 행렬)을 만들기 위해 다음과 같이 \( U \)의 각 행을 \( D \)의 pivot으로 나눠주면 된다.

2.1 The Cost of Elimination
■ \( n \times n \)행렬 \( A \)에서 몇 번의 연산을 해야 소거법으로 연립방정식의 해를 구할 수 있는가?에 대한 내용이다. 즉, 소거법으로 연립방정식의 해를 구하기 위해서 얼마나 많은 비용이 드는지(몇 번의 작업을 하는지)
■ 예를 들어, \( n = 100 \)이고 행렬 \( A \)의 원소에 0이 하나도 없다고 가정해 보자.
- 적절한 위치에 0이 많이 있으면, 미지수 개수가 수백만 개여도 0으로 인해, 원소에 0이 하나도 없는 동일한 크기의 행렬 연산보다 연산이 훨씬 더 빨라지기 때문이다.
- 즉, 행렬 \( A \)의 원소에 0이 하나도 없다고 가정하는 것은 최악의 상황을 가정하기 위함이다.
■ 이제, 소거법의 첫 번째 단계를 생각해 보자. 첫 번째 단계는 첫 번째 pivot 아래의 값들을 모두 0으로 만든다. 이를 위해선 pivot 아래의 행별로 한 번의 곱셈과 한 번의 뺄셈이 필요하다.
■ 행렬 \( A \)의 크기가 \( n \times n \)일 때, 첫 번째 단계에서는 첫 번째 pivot이 있는 행은 업데이트하지 않으므로, 2행부터 \( n \)행까지 총 \( (n-1) \)개 행에 대해, 각 행마다 곱셈 1회, 뺄셈 1회를 열 개수 \( n \)만큼 수행하므로 첫 번째 단계의 연산 횟수는 \( (n-1) \times n = n^2 - n \)이 된다.
- \( n = 100 \)이라면, 필요한 연산(곱셈 1회 + 뺄셈 1회)의 횟수는 9,900번이다.
- 즉, 총 9,900번의 곱셈과 9,900번의 뺄셈 연산이 수행된다.
■ 정확한 연산 횟수는 위와 같지만, \( n \)에 비해 \( n^2 \)이 훨씬 더 크기 때문에 첫 번째 단계에서 필요한 곱셈과 뺄셈의 연산 횟수를 약 \( n^2 \)으로 생각하자.
- 마치 시간 복잡도 \( O(n^2+2n+1) \)을 \( O(n^2) \)으로 보는 것처럼
■ 다음 단계는 두 번째 pivot 아래의 값들을 모두 0으로 만드는 단계이다. 현재 단계에서 작업할 행렬의 크기는 \( n - 1\)이다. 즉, 이 단계에서 필요한 곱셈과 뺄셈의 연산 횟수는 약 \( (n-1)^2 \)이 필요하다.
■ 그렇다면, \( n \times n \)행렬 \( A \)의 해를 구하기 위해(정확히는 연립방정식의 해를 구하기 위해) 대각선 원소가 pivot인 상삼각행렬 \( U \)를 구하기 까지의 곱셈과 뺄셈의 연산 횟수는 \( n^2 + (n-1)^2 + \cdots + 3^2 + 2^2 + 1^1 \)이 된다.
■ \( n^2 + (n-1)^2 + \cdots + 3^2 + 2^2 + 1^1 \)는 \( n^2 + (n-1)^2 + \cdots + 3^2 + 2^2 + 1^1 = \dfrac{n(n+1)(2n+1)}{6} \approx \dfrac{n^3}{3} \)이 된다.
■ 즉, \( n \times n \) 행렬 \( A \)에서 가우스 소거법을 통해 \( U \)를 만들기 위해서는 대략 \( \dfrac{n^3}{3} \)의 곱셈과 \( \dfrac{n^3}{3} \)의 뺄셈이 필요하다.
- 보통 한 번의 행 업데이트(여기서는 elimination)마다 '곱셈 1회 + 뺄셈 1회'식으로 짝을 이루기 때문에, 두 연산을 합치면 대략 \( \dfrac{2}{3} n^3 \)정도가 된다.
■ 그리고 행렬 \( A \)의 크기가 \( n \times n \)이라면, 우변 \( b \)의 크기는 \( n \times 1 \)일 것이다.
■ 이때, \( b \)의 연산 횟수는 첫 번째 단계에서 \( b_1 \)에 multiplier를 곱한 값을 \( b_2, b_3, \cdots, b_n \)에서 뺄 것이다. 이 과정에서 \( n-1 \)번의 연산이 필요하다.
■ 두 번째 단계에서는 \( b_1 \)을 포함하지 않고 연산을 하기 때문에 \( n-2 \)번의 연산이 필요할 것이다. 그러므로 \( b_n \)까지 연산(곱셈 1회 + 뺄셈 1회) 횟수는 \( (n-1) + (n-2) + \cdots + 1 \)이 된다.
■ 이 과정이 모두 끝나면, 해를 구하기 위해 역 대입을 수행해야 한다. 미지수가 \( x_1, x_2, \cdots, x_n \)이라면, \( x_n \)을 구하기 위해서는 마지막 pivot을 나누는 연산만 필요하고, \( x_1 \)을 구하기 위해서는 \( n-1 \)개의 다른 미지수를 대입한 후, 첫 번째 pivot으로 나눠야 한다.
■ 즉, \( b \)에 대한 모든 비용은 \( [(n-1) + (n-2) + \cdots + 1] + [1 + 2 + \cdots + (n-1) + n] = \dfrac{n(n-1)}{2} + \dfrac{n(n+1)}{2} = n^2 \)이 된다.
3. Permutation Matrices
■ 치환행렬(permutation matirx) 은 단위행렬에서 행의 순서가 바뀐 행렬로, 각 행과 열에 오직 하나의 '1'만 가지고 나머지 성분은 모두 0인 행렬이다.
■ 가장 간단한 치환행렬은 단위행렬이다. 그다음, 간단한 치환행렬은 단위행렬의 \( i \)행과 \( j \)행이 바뀐 행렬이다.
■ 즉, 단위행렬 \( I \)에 가능한 모든 행 교환(row exchanges) 을 수행함으로써 가능한 모든 치환행렬을 얻을 수 있다. 그러므로 가능한 모든 치환 행렬의 조합은 \( n! \)이 된다.
- 예를 들어 단위행렬 \( I \)의 크기가 \( 3 \times 3 \)이라면, 가능한 모든 치환 행렬의 조합(가능한 '1'을 재정렬할 수 있는 경우의 수)은 다음과 같이 \( 3! = 6 \)가지이다.

- \( P_{21}(=P_{12}) \)는 단위행렬에서 1행과 2행을 교환한 행렬이다.
- 서로 다른 \( P \)를 곱했을 때, (예를 들어 \( P_{32}P_{21} \)) 다시 치환행렬이 되는 것을 볼 수 있다.
■ 이러한 치환행렬은 모두 역행렬이 가능하다. 왜냐하면, 역행렬이 존재하는 단위행렬에서 행의 순서만 바뀌는 식으로 파생되었기 때문이다.
■ 이때, 치환행렬 \( P \)의 역행렬 \( P^{-1} \)은 \( P^{-1} = P^T \)가 성립한다. \( PP^{T} \)에서 \( P^{T} \)의 1과 \( P \)의 1이 만나 단위행렬의 1이 되기 때문이다. \( P^{T}P = I \)
- 다른 관점에서 보면, \( P^{-1} = P^{T} \)가 성립하는 다른 이유는 \( P \)가 직교행렬이기 때문이다.
■ \( P^{T}P = I \)가 되어 \( P^{-1} = P^T \)가 성립한다. 즉, 치환행렬 \( P \)는 가역행렬이고, 그 역행렬은 \( P^{T} \)이다.
3.1 The \( PA = LU \) Factorization with Row Exchanges
■ 치환행렬은 행 교환이 필요한 경우 사용하는 방법이다. 위의 \( A = LU \) 예시들은 모두 행 교환이 필요 없는 경우를 상정한 경우이다.
■ 하지만 행렬 소거 과정에서 항상 행 교환이 필요 없는 완벽한 행렬만 존재할 수 없기 때문에 행 교환이 필요할 때가 있다.
■ 예를 들어, 다음과 같이 행렬 \( A \)가 다음과 같다면, 소거 과정에서 두 번째 피벗 자리에 0이 오기 때문에 일반적인 과정으로는 분해를 진행할 수 없다.

■ 이런 경우 다음과 같이 행렬 \( P \)를 행렬 \( A \)에 곱해 \( A \)의 행을 교환해서 분해를 진행할 수 있다.

■ 이때, 치환행렬 \( P \)는 \( P^{-1} = P^{T} = P \)이므로 다음과 같이 \( A = PLU \)로 나타낼 수 있다.
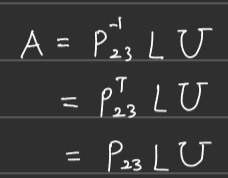
cf) 치환행렬 \( P \)는 단순히 \( A \)의 행 순서만 교환하는 역할이기 때문에, \( PA = LU \)에서 \( PA = LDU \)로 나타내도 상관없다.
'선형대수' 카테고리의 다른 글
| [개념] 벡터 공간 (0) | 2025.01.20 |
|---|---|
| Spaces of Vectors - (1) Vector Spaces and Subspaces (0) | 2025.01.20 |
| [개념] 행렬 (3) (0) | 2025.01.18 |
| [개념] 행렬 (2) (0) | 2025.01.18 |
| [개념] 행렬 (1) (1) | 2025.01.17 |



