1. The Column Space of A
■ 예를 들어 다음과 같은 행렬 \( A \)가 있다고 할 때

■ 행렬 \( A \)는 3개의 열을 가지고 있다. 이 열들은 벡터이므로 3개의 열벡터를 가지고 있는 것으로 볼 수 있다.
■ 이 예에서 행렬 \( A \)의 열공간은 \( \mathbb{R}^4 \)의 부분공간이다. 왜냐하면 \( A \)는 \( 4 \times 3 \)행렬이기 때문이다.
■ 이는 행의 개수, 즉 열의 구성 요소 수가 4개이기 때문이다.
■ 일반화하면, 행렬 \( A \)의 크기가 \( m \times n \)일 때, \( A \)의 열들은 \( m \)개의 성분을 가진다. 즉, \( \mathbb{R}^m \)에 속한다. 그리고 \( A \)의 열 공간은 \( \mathbb{R}^m \)의 부분 공간이다.
■ 다시 돌아와서, 행렬 \( A \)의 열공간은 \( \mathbb{R}^4 \)의 부분공간이다.
■ 이 부분공간에는 \( A \)의 열벡터 \( [1, 2, 3, 4]^T, [1, 1, 1, 1]^T, [2, 3, 4, 5]^T \). 즉, \( A \)의 열들이 포함되어 있지만, 단순히 이 3개의 벡터를 넣는다고 해서 부분공간이 되지는 않고, 이 열벡터들의 선형 결합의 결과 집합이 부분공간이 될 수 있다.
■ 이때, 이 세 벡터의 선형 결합으로 (전체) 4차원 공간을 채울 수 없다. 행렬 \( A \)의 열공간이 \( A \)의 열벡터들의 모든 선형 결합으로 이루어진 집합이며, 주어진 열벡터들이 현재 다음과 같다.

■ 이 세 벡터의 선형 결합으로 만들어지는 집합은 다음과 같다.

■ 이 집합이 \( \mathbb{R}^4 \) 전체가 되려면, 임의의 \( \mathbf{x} \in \mathbb{R}^4 \)를 적절한 \( c_1, c_2, c_3 \)에 대해 다음과 같이 선형 결합의 형태로 나타낼 수 있어야 한다.

■ 하지만 이 예시에서는 3개의 열벡터가 선형 종속 관계를 가지므로 열벡터 \( v_1, v_2, v_3 \)으로 4개의 독립적인 방향을 모두 생성할 수 없으므로 \( \mathbb{R}^4 \)를 채울 수 없다.
- 반면, \( \mathbb{R}^4 \)의 표준 기저는 다음과 같이 선형 독립 관계를 갖는 4개의 벡터로 선형 결합을 통해 \( \mathbb{R}^4 \) 공간에 있는 벡터를 모두 생성할 수 있다. 즉, \( \mathbb{R}^4 \)를 채울 수 있다.

1.1 열공간과 선형 방정식(Linear Equation)
■ 선형 방정식 \( A \mathbf{x} = b \)는 행렬 \( A \)의 열벡터의 선형 결합과 밀접하게 연관되어 있다.
■ 여기서도 행렬 \( A \)가 다음과 같다고 할 때,

■ \( A \mathbf{x} = b \)는 모든 우변 \( b \)에 대해 해를 가지지 않는다.
■ 왜냐하면, 이 예에서 \( A \mathbf{x} = b \)는 4개의 방정식과 3개의 미지수로 이루어져 있기 때문이다.

■ \( A \mathbf{x} = b \)에서 \( A \mathbf{x} \)는 행렬 \( A \)의 열들의 선형 결합으로 나타낼 수 있다.

여기서 가능한 모든 \( b = [ x_1, x_2, x_3]^T \)를 구하라면, 가능한 모든 \( \mathbf{x} \)를 사용해야 한다.
■ 열공간 \( C(A) \)는 \( A \)의 \( n \)개의 열뿐만 아니라 그것들의 모든 결합 \( Ax \)를 포함한다.
■ 열공간은 열들의 모든 선형 결합으로 구성된다. 이 결합은 모든 가능한 벡터 \( Ax \)를 나타낸다.
■ \( Ax = b \)를 푸는 것은 \( b \)를 \( A \)의 열들의 결합으로 표현하는 것이다. \( b \)는 \( A \)가 생성하는 열 공간에 속해야만 해가 존재한다. 그렇지 않으면 해가 존재하지 않는다.
■ 이는 \( A \)의 열벡터의 선형 결합으로 \( \mathbf{R}^4 \) 공간 전체를 생성할 수 없다고 한 것과 동일한 의미이다.
- \( A \)의 세 열벡터 중 \( [1, 2, 3, 4]^T \)와 \( [1, 1, 1, 1]^T \)의 선형 결합으로 \( [2, 3, 4, 5]^T \)를 만들 수 있기 때문에 \( [2, 3, 4, 5]^T \)가 없어도,
- 나머지 두 개의 열벡터로 만든 열공간과 \( [2, 3, 4, 5]^T \)가 포함된 세 개의 열벡터로 만든 열공간은 같은 공간을 만들 것이며,
- 이 예시에서 \( A \)의 열공간은 \( \mathbb{R}^4 \) 안의 작은 평면이나 혹은 평면보다 더 작은 어떤 공간을 만들게 된다. 이 상태에서는 절대 \( \mathbb{R}^4 \) 공간 전체를 생성할 수 없다.
-- 참고로 이 예에서 \( [1, 2, 3, 4]^T \)와 \( [1, 1, 1, 1]^T \)처럼 상호 독립적인 열벡터를 'pivot column'이라고 부른다.
-- 이 예에서는 \( [1, 2, 3, 4]^T \)가 \( \mathbb{R}^4 \)안 에서 하나의 선을 만들고 \( [1, 1, 1, 1]^T \)가 또 다른 독립적인 선을 만드는데, 이 둘의 조합으로 하나의 평면을 만들 수 있다.
-- 이때 \( [2, 3, 4, 5]^T \)는 이 평면 위에 존재하기 때문에 새로운 축(차원)을 만드는 데 어떠한 기여도 할 수 없는 것이다. 그러므로 이 예에서 \( A \)의 열공간은 4차원 공간에서 최대로 생성할 수 있는 공간이 2차원 공간인 평면인 것이다.
-- 그러므로 이 예에서 행렬 \( A \)의 열공간은 \( \mathbb{R}^4 \)의 2차원 부분공간이라고 말할 수 있다.
■ 정리하면, \( A \mathbf{x} = b \)에 대해 벡터 \( b \)가 \( A \)의 열공간에 존재할 때에만 해를 구할 수 있다. 여기서 \( b \)가 \( A \)의 열공간에 존재한다는 것은 '\( b \)가 \( A \)의 열벡터들의 선형 결합으로 표현이 가능할 때'를 말한다. 그리고 여기서(선형 방정식) 말하는 선형 결합은 \( A \mathbf{x} \)를 뜻한다.
■ \( b \)가 열공간에 있을 때, \( b \)는 열벡터들의 결합이다. 이러한 결합에서의 계수들은 \( Ax = b \)의 해 \( \mathbf{x} \)를 제공한다.
- 예를 들어 다음과 같이 \( [1, 0, 0]^T \)나 \( [1, 1, 0]^T \) 등이 있다.
2. Nullspace
■ 선형 방정식 \( A \mathbf{x} = b \)에서 \( b \)가 영벡터일 때, 즉 \( A \mathbf{x} = 0 \)일 때 집합 \( \mathbf{x} \)를 \( A \)의 영공간이라고 한다.
■ 예를 들어 \( A \mathbf{x} = 0 \)이 다음과 같다면,

집합 \( \mathbf{x} \)의 원소가 될 수 있는 것은 \( \mathbf{x} = \left\{ [0, 0, 0]^T, [1, 1, -1]^T, \cdots \right\} \)이며, 이때 임의의 스칼라를 \( c \)라고 하면 \( \mathbf{x} \)는 \( \mathbf{x} = c \cdot [1, 1, -1]^T \)로 정의할 수 있다.
■ 즉, \( c \cdot [1, 1, -1]^T \)가 만드는 직선(또는 공간)이 바로 \( A \)의 영공간이다.
■ 영공간이 벡터 공간인지 확인하는 방법은 동일하다. 단, 영공간이므로 해집합 \( \mathbf{x} \)에 있는 어떤 해를 \( v \), 또 다른 해를 \( w \)라고 했을 때, 행렬 \( A \)와의 곱을 통해 0이 될 수 있는지( \( Av = 0, Aw = 0 \) )이 성립하는지, 그리고 두 벡터를 더한 결과를 \( A \)와 곱했을 때 0이 될 수 있는지( ( \( A(v+w) = 0 \) )를 확인하면 된다.
■ 그리고 스칼라를 곱했을 때도 성립하는지 확인해야 하는데, ( \( A (c\mathbf{x}) = 0 \) ) 여기서 \( c \)는 스칼라이므로 \( c A \mathbf{x} = 0 \)이므로 \( A (c\mathbf{x}) = 0 \)은 성립한다.
- 혹은 \( \mathbf{x} = c \cdot [1, 1, -1]^T \)일 때, \( A \mathbf{x} = 0 \)인데, \( \mathbf{x} \)가 만드는 공간이 벡터 공간이 될 수 있는지를 확인하는 과정이므로,
- 스칼라 \( c \)를 곱한다고 해도 \( \mathbf{x} = c^2 \cdot [1, 1, -1]^T \)이며, \( c^2 \)도 결국 스칼라이므로 \( A (c\mathbf{x}) = 0 \)은 성립한다고 할 수 있다.
■ 우선 \( c \)는 스칼라이므로 \( c \cdot [1, 1, -1]^T \)가 만드는 공간 안에는 영벡터가 포함되어 있다.
■ 또한 \( Av = 0, Aw = 0 \)이 성립하기 때문에 \( v, w \)가 영공간에 포함되므로 \( v \)와 \( w \)의 합인 \( v + w \)도 영공간에 속한다고 할 수 있다.
- \( A(v+w) = 0 \)은 \( Av + Aw = 0 \)이며 \( Av = Aw = 0 \)이므로 \( A(v+w) = 0 \)이 성립할 수밖에 없다.
■ 그러므로 \( A \)의 영공간은 벡터 공간이라고 할 수 있다.
■ 만약, 다음과 같이 우변 \( b \)가 임의의 값을 가진다면, \( \mathbf{x} \)는 벡터 공간이 될 수 있을까?
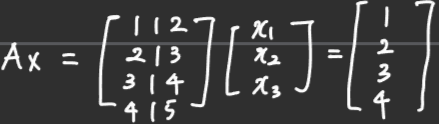
■ 우변 \( b = [1, 2, 3, 4]^T \)라면, \( \mathbf{x} \)의 원소. 즉, 해는 \( [1, 0, 0]^T, [0, -1, 1]^T \)가 가능하다. 어떤 집합이 벡터 공간이 되기 위해서는 집합에 영벡터가 존재해야 하는데, 영벡터가 없으므로 조건을 만족하지 않는다. 그러므로 이 해들( \( [1, 0, 0]^T, [0, -1, 1]^T \) )은 벡터 공간이 될 수 없다.
'선형대수' 카테고리의 다른 글
| [개념] 정규직교집합과 Gram-Schmidt 직교화 (0) | 2025.01.24 |
|---|---|
| [개념] 행렬의 기본 공간과 차원 정리 (0) | 2025.01.22 |
| [개념] 벡터 공간 (0) | 2025.01.20 |
| Spaces of Vectors - (1) Vector Spaces and Subspaces (0) | 2025.01.20 |
| Solving Linear Equations - (4) Inverse Matrices, (5) Elimination = Factorization: A = LU, (6) Permutations (0) | 2025.01.18 |



