참고) 합성곱 신경망(CNN) (1)
합성곱 신경망(CNN) (1)
1. 합성곱 신경망(Convolutional Neural Network, CNN)■ CNN은 이미지 인식, 음성 등 다양한 곳에 사용되며, 특히 이미지 인식 분야에서 활용도가 높다.■ 인접한 계층간 모든 뉴런이 연결된 완전 연결 계층
hyeon-jae.tistory.com
1. Sequential API로 모델 생성
■ CNN 모델은 다음 그림과 같이 이미지에 대한 특징을 추출한 다음, 추론을 위해 평탄화한 후 출력층에 데이터를 넣게 된다.
■ 따라서 합성곱 계층은 Conv2D 레이어, 풀링 계층은 최대 풀링이나 평균 풀링 레이어를 사용하고 FCN으로 넘어가기 위해 CNN 부분이 끝나면 데이터를 평탄화하기 위해 Flatten 레이어를 사용한다.
■ 그리고 마지막으로 추론을 하기 위해 Dense 레이어를 사용한다.

■ 예를 들어 mnist 데이터 셋을 사용해서 Sequential API로 모델을 생성해 보자.
from tensorflow import keras
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# 정규화
x_train = x_train / 255
x_test = x_test / 255
from sklearn.model_selection import train_test_split
x_train, x_valid, y_train, y_valid = train_test_split(x_train, y_train, test_size = 0.2, shuffle=True, random_state = 2024)■ mnist 데이터는 색상을 나타내는 채널이 1개인 모노 컬러 이미지로 CNN 모델에 넣기 위해서 색상을 나타내는 채널을 추가해 준다.
■ 텐서플로에서는 이미지를 표현할 때 (N, H, W, C) 표현 방법을 사용한다. 따라서 (N, H, W, C) 표현처럼 마지막 위치에 채널 수를 표현하고자 가장 마지막 축에 새로운 축을 추가한다.
■ 다음과 같이 채널을 추가하고자 하는 위치에 tf.newaxis를 입력하면 된다.
x_train = x_train[...,tf.newaxis]
x_valid = x_valid[...,tf.newaxis]
x_test = x_test[..., tf.newaxis]
print(x_train.shape, x_valid.shape, x_test.shape) # (N, H, W, C)
```#결과#```
(48000, 28, 28, 1) (12000, 28, 28, 1) (10000, 28, 28, 1)
````````````HE = tf.keras.initializers.HeNormal(seed=2024)
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, (3, 3), kernel_initializer = HE, activation = 'relu', # Conv2D(32, (3, 3)은 서로 다른 3 x 3 크기의 필터 32개
input_shape = (28, 28, 1), name = 'Conv'),
tf.keras.layers.MaxPooling2D((2, 2), name = 'Pooling'),
tf.keras.layers.Flatten(name = 'Flatten'), # 평탄화
tf.keras.layers.Dense(10, activation = 'softmax', name = 'Output')], name='SequentialModel')
model.summary()
```#결과#```
Model: "SequentialModel"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
Conv (Conv2D) (None, 26, 26, 32) 320
Pooling (MaxPooling2D) (None, 13, 13, 32) 0
Flatten (Flatten) (None, 5408) 0
Output (Dense) (None, 10) 54090
=================================================================
Total params: 54,410
Trainable params: 54,410
Non-trainable params: 0
_________________________________________________________________
````````````model.input
```#결과#```
<KerasTensor: shape=(None, 28, 28, 1) dtype=float32 (created by layer 'Conv_input')>
````````````
model.output
```#결과#```
<KerasTensor: shape=(None, 10) dtype=float32 (created by layer 'Output')>
````````````
model.layers
```#결과#```
[<keras.layers.convolutional.conv2d.Conv2D at 0x1c289ea29d0>,
<keras.layers.pooling.max_pooling2d.MaxPooling2D at 0x1c29f87fe80>,
<keras.layers.reshaping.flatten.Flatten at 0x1c289f34f70>,
<keras.layers.core.dense.Dense at 0x1c289f34c10>]
````````````
model.layers[0].input
```#결과#```
<KerasTensor: shape=(None, 28, 28, 1) dtype=float32 (created by layer 'Conv_input')>
````````````
model.layers[0].output
```#결과#```
<KerasTensor: shape=(None, 26, 26, 32) dtype=float32 (created by layer 'Conv')>
````````````- 합성곱 계층의 32, (3, 3)은 서로 다른 3 x 3 크기의 필터(커널) 32개를 적용한 것이다.
- 적용한 결과 (28, 28, 1) 형태의 입력 텐서가 Conv2D를 거쳐 (26, 26, 32) 형태로 변환된다. 이는 3 × 3 필터를 적용했기 때문에 높이, 너비의 크기가 2씩 줄어든 것이다.
- Conv2D를 거쳐 (26, 26, 32) 형태로 변환된 것은 26 × 26 크기의 피처맵이 32개 생성된 것이다. 즉, (H, W, C) = (28, 28, 1) 이미지에 서로 다른 필터 32개를 적용해서 32가지의 피처(특징)를 추출한 것이다.
- 그 다음 2 × 2 크기의 최대 풀링 계층을 거쳐 이미지 크기가 1/2 줄어들어 (13, 13, 32) 텐서로 변환된다.
- 그리고 (13, 13, 32) 텐서는 평탄화를 거쳐 13 × 13 × 32 = 5408 개의 원소를 갖는 1차원 벡터로 변환된다.
■ 이렇게 model.layers[i].output으로 특성 추출을 수행하여 이 특성을 재사용할 수도 있다.
■ 만약, 필터의 가중치와 편향을 확인하고 싶으면 model.layers에 weights 속성을 확인해 보면 된다.
model.layers[0].weights
```#결과#```
[<tf.Variable 'Conv/kernel:0' shape=(3, 3, 1, 32) dtype=float32, numpy=
array([[[[-6.71858013e-01, -5.36292493e-01, -2.02654466e-01,
5.67673519e-02, -1.03641199e-02, -8.14229190e-01,
...,
3.70377660e-01, 8.36726785e-01, 5.70084155e-01,
5.43041751e-02, -2.47111339e-02]]]], dtype=float32)>,
<tf.Variable 'Conv/bias:0' shape=(32,) dtype=float32, numpy=
array([0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
dtype=float32)>]- Conv/kernel:0이 필터의 가중치, Conv/bias:0가 필터의 편향이며, 다음과 같이 필터의 가중치와 편향을 따로 확인할 수도 있다.
model.layers[0].kernel # 필터 가중치
model.layers[0].bias # 필터 편향- 첫 번째 레이어의 필터 가중치와 편향의 크기를 보면
model.layers[0].kernel.shape, model.layers[0].bias.shape
```#결과#```
(TensorShape([3, 3, 1, 32]), TensorShape([32]))
````````````필터의 형상은 이미지 데이터의 형상 (N, H, W, C)와 다른 것을 볼 수있다. 이는 필터의 형상은 (Height, Width, in_Channels, out_ Channels )이기 때문이다.
- 따라서 (3, 3, 1, 32)의 의미는 3 × 3 크기, 입력층의 채널 개수는 1, 출력층의 채널 개수는 32를 의미하며, 업데이트 가능한 파라미터의 수는 3 × 3 × 1 × 32 = 288개가 된다.
- 이때 편향이 32개 이므로, 총 업데이트 가능한 파라미터 수는 288 + 32 = 320개가 된다.
■ 풀링은 최대 풀링을 적용했는데, 최대 풀링은 지정한 크기(이 예에서는 2 × 2)의 픽셀들 중에서 최댓값을 가져오기 때문에 풀링을 통해 픽셀 수는 줄어들면서 이미지의 특징이 더 강하게 나타난다.
■ 이를 확인하기 위해 다음과 같이 입력의 형상이 (None, 28, 28, 1)이고 합성곱 계층과 최대 풀링 계층으로만 이루어진 새로운 모델을 다음과 같이 정의한다.
activator = tf.keras.Model(inputs = model.input,
outputs = [layer.output for layer in model.layers[:2]]) # conv layer, max polling layer
activator.summary()
```#결과#```
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
Conv_input (InputLayer) [(None, 28, 28, 1)] 0
Conv (Conv2D) (None, 26, 26, 32) 320
Pooling (MaxPooling2D) (None, 13, 13, 32) 0
=================================================================
Total params: 320
Trainable params: 320
Non-trainable params: 0
_________________________________________________________________
````````````
activations = activator.predict(x_train[0][tf.newaxis,...])- 모델을 훈련시키지 않고 첫 번째 이미지로 두 계층을 비교하기 위해 x_train[0]의 데이터를 가져와서 추론을 수행한다.
- 이때 x_train[0]의 형상은 (28, 28, 1)로 3차원이기 때문에 predict( )을 수행할 수 없다.
- 따라서 (N, H, W, C)으로 타입을 맞춰주기 위해 새로운 축을 추가한다.
■ 두 계층만 사용했기 때문에 activations[0]은 Conv2D 레이어의 출력, activation[1]은 Maxpolling2D까지 적용했을 때의 레이어의 출력이다.
activations[0].size, activations[1].size
```#결과#```
(21632, 5408)
````````````
26*26*32, 13*13*32
```#결과#```
(21632, 5408)
````````````■ 두 층의 출력 피처 맵 이미지를 32개 커널별로 시각화하면 다음과 같다.
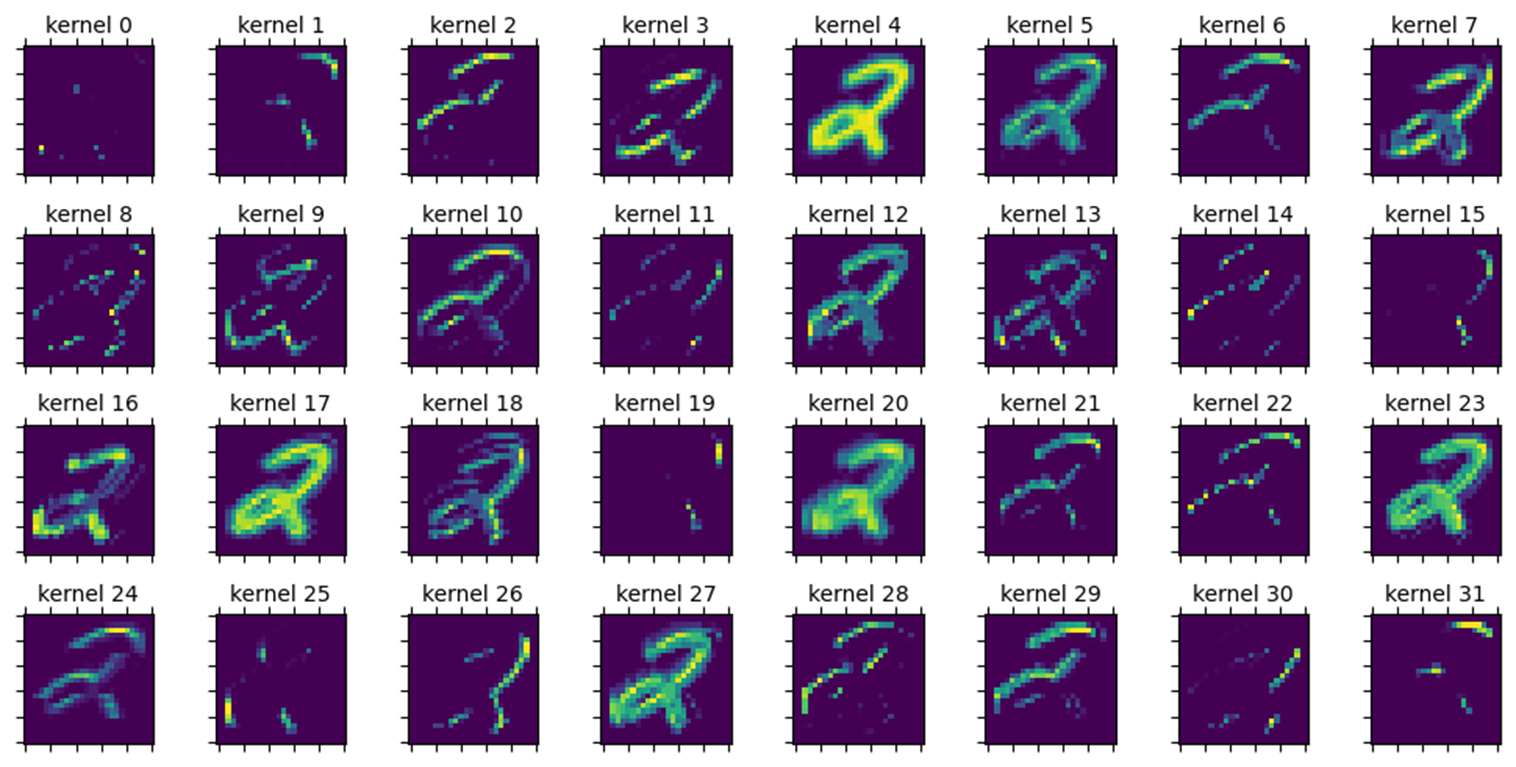

- 두 개의 출력 피처 맵 모두 각 커널별 이미지가 조금씩 다른 것을 볼 수 있다. 이는 32개의 커널이 동일한 입력 이미지로부터 서로 다른 피처(특징)을 추출하기 때문이다.
- 그리고 합성곱 계층의 출력 피처 맵보다 최대 풀링 계층의 출력 피처 맵의 이미지가 더 특징이 강하게 드러난 것을 볼 수 있다.
아래 학습 컴파일 그래프 결과는 필요 없지 않을까? 맨날 하던건데 일단 생략하고 보자.
def scheduler_function(epoch, lr):
if epoch < 10: return lr
else:return lr * tf.math.exp(-0.1)
lr_scheduler = keras.callbacks.LearningRateScheduler(scheduler_function)
model.compile(
optimizer = tf.keras.optimizers.Adam(learning_rate=0.01, beta_1 = 0.9, beta_2 = 0.99),
loss = tf.keras.losses.SparseCategoricalCrossentropy(),
metrics = [tf.keras.metrics.SparseCategoricalAccuracy()]
)
history = model.fit(x_train, y_train, batch_size = 128, validation_data=(x_valid, y_valid),
epochs=30, callbacks = [lr_scheduler])
model.evaluate(x_test, y_test)
```#결과#```
375/375 [==============================] - 2s 3ms/step - loss: 0.1515 - sparse_categorical_accuracy: 0.9858
[0.15146490931510925, 0.9858333468437195]
````````````
- 검증 데이터에 대해 약 98%의 정확도를 나타낸다.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1, 3, figsize=(12, 3))
# 손실 값 변화 그래프
ax[0].plot(history.history['loss'], label='Training Loss')
ax[0].plot(history.history['val_loss'], label='Validation Loss')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('Loss')
ax[0].legend('')
# 정확도 변화 그래프
ax[1].plot(history.history['sparse_categorical_accuracy'], label='Training Accuracy')
ax[1].plot(history.history['val_sparse_categorical_accuracy'], label='Validation Accuracy')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Accuracy')
ax[1].legend()
# 학습률 변화 그래프
ax[2].plot(history.history['lr'], label='Learning Rate')
ax[2].set_xlabel('Epochs')
ax[2].set_ylabel('Learning Rate')
ax[2].legend()
plt.tight_layout()
plt.show()
- epoch 5 이후부터 모델이 과적합되는 것을 볼 수 있다.
2. FunctionalAPI로 모델 생성
■ 함수형 API로 모델을 만들면 다중 입력, 다중 출력, 분기 & 병합을 가지거나 중간에 있는 레이어들을 건너뛰고 뒤쪽에 있는 레이어로 출력을 전달하는 복잡한 구조의 모델을 만들 수 있다.
■ 예를 들어 다음과 같이 Conv 레이어와 Flatten 레이어의 입력으로 하나의 입력 레이어를 받아서 Conv 레이어는 Pooling 레이어를 거쳐 데이터를 평탄화하고, Flatten 레이어는 입력 데이터를 바로 평탄화한 다음, 두 결과를 Concatenate 레이어에서 합칠 수 있다.
HE = tf.keras.initializers.HeNormal(seed=2024)
inputs = tf.keras.layers.Input(shape = (28, 28, 1), name = 'inputs')
conv = tf.keras.layers.Conv2D(32, (3, 3), kernel_initializer = HE, activation = 'relu', name = 'convd')(inputs)
pool = tf.keras.layers.MaxPooling2D((2, 2), name = 'maxpool')(conv)
flat = tf.keras.layers.Flatten(name = 'flatten')(pool)
flat_inputs = tf.keras.layers.Flatten()(inputs)
concat = tf.keras.layers.Concatenate(name = 'concat')([flat, flat_inputs])
outputs = tf.keras.layers.Dense(10, activation = 'softmax', name = 'outputs')(concat)
model = tf.keras.models.Model(inputs = inputs, outputs = outputs)
model.summary()
```#결과#```
Model: "model_7"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
inputs (InputLayer) [(None, 28, 28, 1)] 0 []
convd (Conv2D) (None, 26, 26, 32) 320 ['inputs[0][0]']
maxpool (MaxPooling2D) (None, 13, 13, 32) 0 ['convd[0][0]']
flatten (Flatten) (None, 5408) 0 ['maxpool[0][0]']
flatten_16 (Flatten) (None, 784) 0 ['inputs[0][0]']
concat (Concatenate) (None, 6192) 0 ['flatten[0][0]',
'flatten_16[0][0]']
outputs (Dense) (None, 10) 61930 ['concat[0][0]']
==================================================================================================
Total params: 62,250
Trainable params: 62,250
Non-trainable params: 0
__________________________________________________________________________________________________
````````````tf.keras.utils.plot_model(model, show_shapes = True, show_layer_names = True)
- 합성곱 - 활성화 함수 - 풀링 계층을 거쳐 추출된 특징을 평탄화한 결과(고수준의 정보)와 flatten_16 레이어 원본 이미지의 특징을 평탄화한 결과(저수준의 정보)를 Concatenate 레이어서 합쳐 출력층에 전달하는 구조이다. 함수형 API는 이렇게 자유롭게 모델 구조를 정의할 수 있다.
cf) 합성곱 층은 특성 공간에 있는 지역 패턴을 학습(예를 들어 MNIST 숫자 이미지에서 특정 픽셀에 걸친 패턴을 학습)하고 Dense 층은 전역 패턴(이미지의 모든 픽셀에 걸친 패턴)을 학습한다.
■ 다른 예로 MNIST 셋에서 이미지가 홀수인지 짝수인지에 대한 정답을 하나 추가해 0~9까지 숫자를 맞추는 분류 문제와 홀수, 짝수를 분류하는 다중 출력 분류 모델을 구현해 보자.
from tensorflow.keras.datasets import mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
```#결과#```
(60000, 28, 28) (60000,)
(10000, 28, 28) (10000,)
````````````
from sklearn.model_selection import train_test_split
x_train, x_valid, y_train, y_valid = train_test_split(x_train, y_train, test_size = 0.2, shuffle=True, random_state = 2024)
print(x_train.shape, y_train.shape)
print(x_valid.shape, y_valid.shape)
print(x_test.shape, y_test.shape)
```#결과#```
(48000, 28, 28) (48000,)
(12000, 28, 28) (12000,)
(10000, 28, 28) (10000,)
````````````■ 홀수 & 짝수 레이블을 다음과 같이 만들며, train, valid, test set에도 동일한 방법으로 홀수 & 짝수 레이블을 만들어 준다.
y_train_odd = []
for y in y_train:
if y % 2 == 0: y_train_odd.append(0) # 짝수면 0
else: y_train_odd.append(1) # 홀수면 1
y_train_odd = np.array(y_train_odd)
y_train_odd.shape
```#결과#```
(48000,)
````````````
print(y_train[:10]); print(y_train_odd[:10]) # 올바르게 홀수, 짝수 레이블을 만들었는지 확인
```#결과#```
[2 9 1 3 8 0 4 4 0 1]
[0 1 1 1 0 0 0 0 0 1]
````````````
print(y_valid[:10]); print(y_valid_odd[:10])
```#결과#```
[0 2 1 1 9 1 5 4 4 3]
[0 0 1 1 1 1 1 0 0 1]
````````````
print(y_test[:10]); print(y_test_odd[:10])
```#결과#```
[7 2 1 0 4 1 4 9 5 9]
[1 0 1 0 0 1 0 1 1 1]
````````````■ 그다음, 데이터를 정규화하고 .MNIST 셋에 채널 축을 추가한다. 색상이 하나인 이미지이므로 채널 개수는 1이다.
- 텐서플로 expand_dims( ) 메서드에 원본 배열과 새롭게 추가하려는 축의 인덱스를 지정하면 된다.
- 축의 인덱스를 -1로 지정하면, 새로운 축은 끝에 추가된다.
## 정규화
x_train = x_train /255.0
x_valid = x_valid /255.0
x_test = x_test /255.0
# 채널 추가
## (N, H, W, C) 형태로 만들기
x_train_in = tf.expand_dims(x_train, -1)
x_valid_in = tf.expand_dims(x_valid, -1)
x_test_in = tf.expand_dims(x_test, -1)
x_train_in.shape, x_valid_in.shape, x_test_in.shape
```#결과#```
(TensorShape([48000, 28, 28, 1]),
TensorShape([12000, 28, 28, 1]),
TensorShape([10000, 28, 28, 1]))
````````````- x_train, x_valid, x_test의 shape이 (N, H, W, C)가 된 것을 볼 수 있다.
- 예를 들어 x_train의 shape은 x_train이 28 x 28 크기의 흑백 이미지 48,000장을 담고 있음을 의미한다.
■ 데이터가 준비되었으면 모델 구조 정의 및 모델 컴파일을 해야 한다.
- 이 예에서 모델은 2개의 출력층을 가져야 한다. 출력층 하나는 다중 분류, 다른 하나는 이진 분류를 다뤄야 하므로
- 다중 분류를 수행하는 출력층의 함수는 softmax, 이진 분류를 수행하는 출력층의 함수는 sigmoid 함수를 지정한다.
- 먼저 이진 분류는 단순히 입력 이미지를 평탄화하고 바로 sigmoid 출력층에 입력값으로 넣어 결과를 계산한다.
- 다중 분류를 수행하는 합성곱 - 활성화 함수 - 풀링 계층의 경우 비선형 문제를 풀어야 하므로 활성화 함수는 relu 함수를 사용하고, relu 함수에 맞춰 가중치 초깃값은 He 초깃값을 사용한다.
- 다중 분류의 경우 첫 번째 합성곱 레이어는 3 x 3 크기의 서로 다른 32가지 종류의 필터(커널)를 적용하고 첫 번째 최대 풀링 계층은 2 x 2 크기의 최대 풀링을 적용한다.
- 첫 번째 합성곱 - 풀링 계층은 패딩을 적용하지 않았으므로 첫 번째 출력 특징 맵의 크기는 줄어들 것이다. 두 번째 합성곱 계층에서는 다른 특징을 추출하고자 패딩을 적용해서 입력과 출력의 크기가 동일하게 유지되도록 설정한다.
- 모든 합성곱 - 풀링 계층을 통과했으면 평탄화를 통해 softmax 출력층에 입력값으로 넣어야 한다.
- 이때, 이진 분류를 수행하기 위해 바로 평탄화한 레이어와 다중 분류를 위해 합성곱 - 풀링 계층을 통과한 후 평탄화한 레이어를 concatenate 레이어로 합쳐서 고수준의 정보와 저수준의 정보를 softmax 출력층의 입력값으로 사용한다.
- 위와 같은 모델 구조를 함수형 API로 정의하면 다음과 같다.
HE = tf.keras.initializers.HeNormal(seed=2024)
inputs = tf.keras.layers.Input(shape = (28, 28, 1), name = 'inputs')
conv = tf.keras.layers.Conv2D(32, (3, 3), kernel_initializer = HE, activation = 'relu', name = 'convd1')(inputs)
pool = tf.keras.layers.MaxPooling2D((2, 2), name = 'maxpool1')(conv)
conv2 = tf.keras.layers.Conv2D(64, (3, 3), kernel_initializer = HE, padding='same',activation = 'relu', name = 'convd2')(pool)
pool2 = tf.keras.layers.MaxPooling2D((2, 2), name = 'maxpool2')(conv2)
flat = tf.keras.layers.Flatten(name = 'flat')(pool2)
flat_inputs = tf.keras.layers.Flatten()(inputs)
concat = tf.keras.layers.Concatenate(name = 'concat')([flat, flat_inputs])
digit_outputs = tf.keras.layers.Dense(10, activation = 'softmax', name = 'outputs_digit')(concat)
odd_outputs = tf.keras.layers.Dense(1, activation = 'sigmoid', name = 'outputs_odd')(flat_inputs)
model = tf.keras.models.Model(inputs = inputs, outputs = [digit_outputs, odd_outputs])
model.summary()
```#결과#```
Model: "model_1"
__________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
==================================================================================================
inputs (InputLayer) [(None, 28, 28, 1)] 0 []
convd1 (Conv2D) (None, 26, 26, 32) 320 ['inputs[0][0]']
maxpool1 (MaxPooling2D) (None, 13, 13, 32) 0 ['convd1[0][0]']
convd2 (Conv2D) (None, 13, 13, 64) 18496 ['maxpool1[0][0]']
maxpool2 (MaxPooling2D) (None, 6, 6, 64) 0 ['convd2[0][0]']
flat (Flatten) (None, 2304) 0 ['maxpool2[0][0]']
flatten_1 (Flatten) (None, 784) 0 ['inputs[0][0]']
concat (Concatenate) (None, 3088) 0 ['flat[0][0]',
'flatten_1[0][0]']
outputs_digit (Dense) (None, 10) 30890 ['concat[0][0]']
outputs_odd (Dense) (None, 1) 785 ['flatten_1[0][0]']
==================================================================================================
Total params: 50,491
Trainable params: 50,491
Non-trainable params: 0
__________________________________________________________________________________________________
````````````- 첫 번째 합성곱의 층의 필터는 32, 두 번째 합성곱 층의 필터는 64로 설정하였다.
- 첫 번째 합성곱 층에서 블롭이나 엣지같은 작은 지역 패턴을 학습하고 두 번째 합성곱 층은 첫 번째 층의 특성으로 구성된 더 추상적인 패턴을 학습한다. 합성곱 층이 깊어질수록 더 복잡하고 추상적인 패턴을 학습할 수 있는데, 이는 합성곱 층이 패턴의 공간적 계층 구조를 학습할 수 있기 때문이다.
- Conv2D 층에서 패딩은 padding 매개변수로 설정할 수 있는데, 디폴트 값은 'valid'이다. 'valid'는 패딩을 사용하지 않는다는 뜻이고 'same'은 입력과 동일한 높이, 너비를 가진 출력을 만들기 위해 패딩한다. 라는 뜻이다.
tf.keras.utils.plot_model(model, show_shapes = True, show_layer_names = True)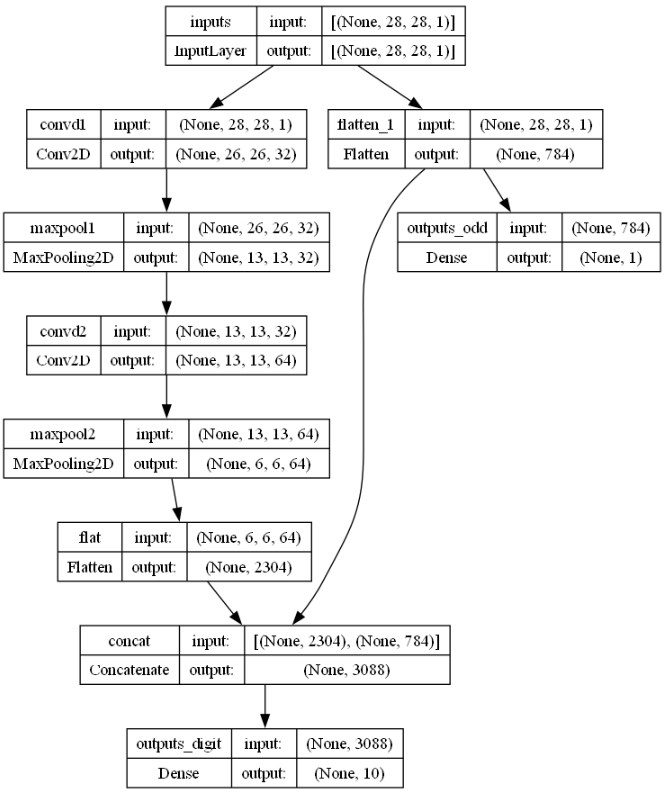
■ 모델 구조를 정의할 때 입력층과 출력층의 이름을 지정해 주었다. 이를 이용해 모델 컴파일 시, 레이어의 이름을 key, 손실 함수와 평가지표를 value로 갖는 딕셔너리 형태로 loss와 metrics 인수를 다음과 같이 설정할 수 있다.
model.compile(
optimizer=tf.keras.optimizers.Adam(learning_rate=0.01, beta_1=0.9, beta_2=0.99),
loss={
'outputs_digit': 'sparse_categorical_crossentropy',
'outputs_odd': 'binary_crossentropy'
}, loss_weights = {'outputs_digit':1, 'outputs_odd':0.5},
metrics={
'outputs_digit': ['sparse_categorical_accuracy'],
'outputs_odd': ['accuracy']
}
)- loss_weight을 적용해 총 손실 계산 과정에 가중치를 부여한다.
- loss_weights = {'outputs_digit':1, 'outputs_odd':0.5}는 outputs_digit 출력 손실에 1을, outputs_odd 출력 손실에 0.5를 곱하겠다는 의미이며, 더 큰 가중치가 부여된 outputs_digit의 손실이 전체 손실에 더 큰 영향을 미치게 된다.
- 전체 손실은 (1.0 × digit_loss) + (0.5 × odd_loss) 형태로 계산된다.
■ 그다음, 모델 훈련 과정에서 fit( ) 메서드를 사용한다면 다중 분류이므로 출력 값을 2개 지정해야 한다. 컴파일 단계와 마찬가지로 층의 이름을 key로 하는 딕셔너리를 이용해 학습할 데이터와 검증할 데이터를 지정할 수 있다.
history = model.fit({'inputs':x_train_in}, {'outputs_digit':y_train, 'outputs_odd':y_train_odd},
validation_data = ({'inputs':x_valid_in}, {'outputs_digit':y_valid, 'outputs_odd':y_valid_odd}),
epochs = 10)
```#결과#``
Epoch 1/10
1500/1500 [==============================] - 12s 7ms/step - loss: 0.3426 - outputs_digit_loss: 0.1973 - outputs_odd_loss: 0.2906 - outputs_digit_sparse_categorical_accuracy: 0.9489 - outputs_odd_accuracy: 0.8804 - val_loss: 0.2623 - val_outputs_digit_loss: 0.1317 - val_outputs_odd_loss: 0.2613 - val_outputs_digit_sparse_categorical_accuracy: 0.9663 - val_outputs_odd_accuracy: 0.8958
Epoch 2/10
1500/1500 [==============================] - 11s 7ms/step - loss: 0.2704 - outputs_digit_loss: 0.1320 - outputs_odd_loss: 0.2768 - outputs_digit_sparse_categorical_accuracy: 0.9703 - outputs_odd_accuracy: 0.8914 - val_loss: 0.2641 - val_outputs_digit_loss: 0.1289 - val_outputs_odd_loss: 0.2703 - val_outputs_digit_sparse_categorical_accuracy: 0.9714 - val_outputs_odd_accuracy: 0.8935
...,
Epoch 10/10
1500/1500 [==============================] - 10s 7ms/step - loss: 0.2237 - outputs_digit_loss: 0.0865 - outputs_odd_loss: 0.2744 - outputs_digit_sparse_categorical_accuracy: 0.9863 - outputs_odd_accuracy: 0.8930 - val_loss: 0.2959 - val_outputs_digit_loss: 0.1625 - val_outputs_odd_loss: 0.2668 - val_outputs_digit_sparse_categorical_accuracy: 0.9785 - val_outputs_odd_accuracy: 0.8967
```````````■ 훈련이 끝나면 unseen data인 test set에 모델을 적용해 모델의 일반화 성능을 평가할 수 있다. 마찬가지로 층의 이름을 key로 하는 딕셔너리를 이용해 테스트 데이터를 지정할 수 있다.
model.evaluate({'inputs':x_test_in}, {'outputs_digit':y_test, 'outputs_odd':y_test_odd})
```#결과#```
313/313 [==============================] - 1s 4ms/step - loss: 0.3241 - outputs_digit_loss: 0.1845 - outputs_odd_loss: 0.2792 - outputs_digit_sparse_categorical_accuracy: 0.9762 - outputs_odd_accuracy: 0.8915
[0.3240967392921448,
0.18449051678180695,
0.27921220660209656,
0.9761999845504761,
0.8914999961853027]
````````````- 평가 결과, 0~9 숫자를 맞추는 문제는 약 98%의 정확도를 보인 반면, 홀짝 여부를 판단하는 문제는 약 89%의 정확도를 보인다. 이진 분류 문제의 경우 레이어를 더 추가해 성능을 개선할 여지가 있다.
■ 마지막으로 모델 예측은, 다중 분류 문제의 경우 predict( ) 메서드를 적용하면 반환된 결과의 인덱스에 문제별 예측 결과가 저장된다. 이 예에서 분류하려는 문제는 두 가지이므로, 인덱스 0에는 숫자 0~9를 예측한 softmax 결과, 인덱스 1에는 홀짝을 예측한 sigmoid 결과가 저장된다.
predictions = model.predict(x_test_in)
# 예측 결과 분리
digit_predictions = predictions[0]
odd_predictions = predictions[1]- softmax와 sigmoid 함수의 결과 모두 확률로 해석할 수 있다.
digit_predictions[0]
```#결과#```
array([1.5933154e-29, 4.6224872e-31, 2.8626088e-18, 5.3283994e-13,
3.0361141e-34, 1.1729945e-25, 0.0000000e+00, 1.0000000e+00,
2.7296402e-22, 1.8299130e-20], dtype=float32)
````````````
np.argmax(digit_predictions[0])
```#결과#```
7
````````````
odd_predictions[0]
```#결과#```
array([0.99978334], dtype=float32)
````````````- 예측 결과 모델은 첫 번째 이미지를 숫자 7, 홀수로 예측했다.
- 실제 첫 번째 이미지의 숫자를 확인해 보면 모델이 첫 번째 이미지에 대해 올바르게 다중 분류를 수행했음을 알 수 있다.
import matplotlib.pylab as plt
def plot_image(data, idx):
plt.figure(figsize = (4, 4))
plt.imshow(data[idx])
plt.axis('off')
plt.show()
plot_image(x_test, 0)

- 예측 결과를 레이블로 만들고 싶은 경우, 첫 번째 예측 결과는 확률이므로 np.argmax를 이용해 가장 큰 값을 가지는 인덱스를 찾으면 되고,
- 두 번째 시그모이드 함수의 결과는 이진 분류 문제이므로 문제를 0과 1로 분류할 임곗값이 필요하다. 만약 임곗값을 0.5로 지정한다면, 홀수일 확률이 0.5보다 큰 경우 홀수로 분류되고 그렇지 않으면 짝수로 분류된다.
digit_labels = np.argmax(digit_predictions, axis = -1)
digit_labels[0:10]
```#결과#```
array([7, 2, 1, 0, 4, 1, 4, 9, 5, 9], dtype=int64)
````````````
odd_labels = (odd_predictions > 0.5).astype(np.int32).reshape(1, -1)[0]
odd_labels[0:10]
```#결과#```
array([1, 0, 1, 0, 0, 1, 0, 1, 0, 1])
````````````
'텐서플로' 카테고리의 다른 글
| 임베딩(Embedding) 순환신경망(Recurrent Neural Network, RNN) (0) | 2025.01.21 |
|---|---|
| 텐서플로 합성곱 신경망(CNN) (2) (0) | 2024.11.22 |
| 케라스(Keras) (2) (2) | 2024.08.20 |
| 케라스(Keras) (1) (0) | 2024.08.18 |
| 텐서(Tensor) (1) (1) | 2024.08.10 |



