1. 합성곱 신경망(Convolutional Neural Network, CNN)
■ 합성곱 신경망CNN은 컨브넷(convnet)이라고도 부르며 이미지 인식, 음성 등 다양한 곳에 사용된다. 특히 이미지 인식 분야에서 활용도가 높다.
■ 인접한 계층간 모든 뉴런이 연결된 완전연결 계층(Fully Connected Layer)은 입력 데이터의 형태가 1차원이라서 이미지 데이터를 입력으로 사용하기 위해 이미지의 픽셀 값들을 1차원 벡터로 평탄화시켰다.
■ 1차원 벡터로 평탄화하는 이유는 완전연결 계층은 다음 그림과 같이 여러 층으로 중첩된 행렬곱의 식이고, 행렬곱 계산은 기본적으로 모든 요소 간의 곱셈 계산을 수행해야 한다.


따라서 이미지 데이터에 행렬 곱 계산을 적용하기 위해 3차원 데이터를 1차원 벡터로 평탄화시켜 입력값으로 사용한다.
■ 컬러 사진은 가로·세로·색상(채널)로 구성된 3차원이다. 이를 평면화시켜 1차원으로 변환하면, 3차원 형상을 고려하지 않고 모든 입력 데이터를 같은 차원의 뉴런으로 간주하여 3차원의 본질적인 패턴이 저장된 이미지 공간 정보(spatial Information)가 손실된다. 이로 인해 이미지의 특징 추출, 학습이 비효율적이게 되고 이는 낮은 정확도로 귀결된다.
■ 예를 들어 다음과 같은 이미지 특정 부분의 픽셀 값이 \( x_{11}, x_{12}, x_{13}, x_{21}, x_{22},.... \)일 때,

이미지 픽셀을 평탄화해서 입력 데이터로 사용하면 \( x_{11} \)과 \( x_{21} \) 픽셀은 서로 매우 가까운 위치에 있는 픽셀이지만, 이러한 지역 정보(region feature)를 전혀 반영할 수 없다.
■ 반면, CNN은 입력 데이터로 3차원 이미지 데이터를 받을 수 있으며, 다음 계층으로도 3차원으로 전달할 수 있다. 따라서 이미지의 공간 정보(spatial Information)를 유지한 상태로 학습이 가능하다.
- 따라서 CNN 구조를 이용하면, 위의 예에서 픽셀 \( x_{11} \)과 가까운 \( x_{12}, x_{21}, x_{22}, \ldots \) 픽셀의 '가까운 정보'까지 함께 학습할 수 있다.
■ 컬러 사진은 가로·세로·색상(채널)로 구성된 3차원인데, 이를 평면화시켜 1차원으로 변환하면, 3차원의 본질적인 패턴이 저장된 이미지 공간 정보가 손실된다.이로 인해 이미지의 특징 추출, 학습이 비효율적이게 되고 이는 낮은 정확도로 귀결된다.
■ 반면, CNN은 입력 데이터로 3차원 이미지 데이터를 받을 수 있으며, 다음 계층으로도 3차원으로 전달할 수 있다. 따라서 이미지의 공간 정보를 유지한 상태로 학습이 가능하다.
■ 하나의 컬러 이미지는 3개의 채널로 구성되며, 각 채널(channel)은 각각의 특징을 가지고 있다.
- 이 3 개의 채널은 red, green, blue 채널이며, red 채널은 '빨간색'이라는 특징, green 채널은 '초록색이라는 특징, blue 채널은 '파란색'이라는 특징을 가지고 있다. 이 3개의 채널을 모두 합하면 다음 예시와 같이 하나의 컬러 이미지가 된다.

■ 예를 들어 높이가 30, 폭이 20인 컬러 이미지 데이터의 형상(shape)은 (C, H, W) = (3, 30, 20)으로 표현되며, 흑백 이미지는 하나의 채널을 가지므로 (1, 30, 20)으로 표현된다.
■ 즉, 채널 수가 1이면 흑백 이미지, 3이면 컬러 이미지이다.
■ 이미지의 픽셀 한 칸 한 칸의 값은 모두 실수로 구성되어 있다. 따라서 컬러 이미지는 각 픽셀을 RGB 3개의 실수로 표현한 '3차원 데이터'라고 할 수 있다.
1.1 CNN 구조
■ 먼저, 완전 열결 계층으로 이루어진 네트워크의 구조는 다음과 같이 Affine 계층, 활성화 함수 계층, 그리고 최종 결과를 출력하는 출력층으로 형성된다.

■ CNN에는 합성곱(Conv) 계층과 풀링(Pooling) 계층이 존재한다.
■ '합성곱 계층 - 활성화 함수 계층 - (풀링 계층)' 흐름으로 연결되며, 풀링 계층을 생략하기도 한다.
■ 그리고 출력에 가까운 층에서는 Affine 계층 - 활성화 함수 계층을 사용할 수 있으며, 인식 결과를 출력하기 위해 Affine 계층 - 출력 계층을 사용한다.
■ 앞 부분에서 Affine 계층을 사용하지 않는 이유는 Affine 계층을 사용하면 공간 정보 손실로 인해 비효율적인 학습과 이미지 특징 추출이 발생하기 때문에 합성곱 계층으로 대체한 것이다.


- CNN은 이미지에 대한 특징을 추출하는 작업을 하고 FCN에서는 어떤 것이 정답인지에 대한 분류 작업을 한다.
1.2 합성곱 계층(Convolution Layer)
■ CNN에서 합성곱 계층의 입출력 데이터를 특징 맵(feature map)이라고 한다.
- 합성곱 계층의 입력 데이터를 입력 특징 맵(input feature map), 출력 데이터를 (output feature map)라고 부르기도 한다.
1.2.1 합성곱 계층에서의 합성곱 연산
■ 합성곱 연산은 이미지 처리에서 말하는 필터 연산에 해당된다.

- 흑백 이미지의 숫자 0은 검은색, 숫자 255는 흰색, 0과 255 중간에 있는 숫자들은 회색으로 표현된다.
- 화소를 나타내는 숫자는 이미지의 강도를 의미하며, 숫자가 클수록 더 강한 특성을 나타내는 것이다.
- 컬러 이미지도 0~255 사이의 숫자로 표현되며, 숫자가 클수록 해당 색상을 더 강하게 표현된다.
■위의 그림과 같이 원본 이미지에 필터를 적용하는 이유는 이미지의 특징을 추출하기 위함이다.
- 필터를 커널(kernel)이라고도 한다.
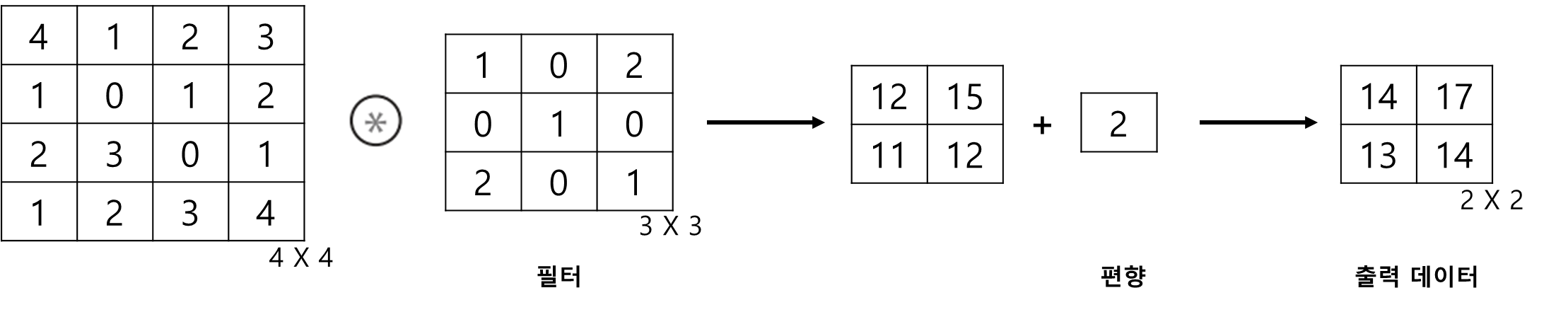
■ 예를 들어 다음과 같이 입력 데이터의 크기가 \( 4 \times 4 \)인 2차원 입력 데이터, 필터도 \( 3 \times 3 \)인 2차원데이터이고, stride = 1 이라면 합성곱 연산의 결과는 다음과 같다.

- 필터(커널)의 사이즈가 3 x 3이면 총 9개의 가중치를 가지며 오차 역전파 시 커널의 가중치를 갱신한다.
■ 위의 예시처럼 합성곱 연산은 입력 데이터에 필터를 적용하여 계산한다.
■ 하나의 입력 데이터와 하나의 필터는 2차원(가로·세로방향의 차원)을 갖는데, 이 형상을 ( 높이(height), 너비(width) )로 표기한다.
- 이 예에서 입력 데이터와 필터를 (높이, 너비)로 표기하면, 입력 데이터는 (4, 4), 필터는 (3, 3), 출력은 (2, 2)
■ 합성곱 연산은 필터의 윈도우(window)를 일정 간격으로 이동해가며 '단일 곱셈-누산'을 수행한다.
- 여기서 윈도우는 필터의 사이즈 (3, 3)을 의미하며, 단일 곱셈-누산은 입력 데이터와 필터에 대응하는 원소끼리 곱한 후 그 총합을 계산한 것이다.


■ CNN에서 필터의 매개변수는 완전연결 네트워크의 가중치에 해당되며, CNN에도 편향이 존재한다.
- 이 예시에서 필터를 적용하고 편향을 더하면 다음과 같은 출력 결과를 얻을 수 있다.
1.2.2 패딩(Padding)과 스트라이드(Stride)
■ 패딩은 주로 출력 데이터의 크기를 조정하기 위해 합성곱 연산을 수행하기 전, 입력 데이터 주변에 특정 값(더미 데이터)을 추가하는 기법이다.
■ 출력 데이터의 크기를 조정하는 이유는 심층 신경망에서 합성곱 연산이 반복된다면, 출력 크기가 계속 작아지기 때문에 어느 시점에서는 출력 크기가 1이 된다.
■ 위의 합성곱 연산 예시에서도 (4, 4) 입력 데이터에 (3, 3) 필터를 적용하니 출력 크기가 입력보다 2만큼 줄어 (2, 2)가 되었다.
■ 출력 크기가 1이 되면 더 이상 합성곱 연산을 할 수 없다. 이 문제를 방지하고자 패딩을 적용하는 것이다.
■ 예를 들어 다음과 같은 (4, 4) 입력 데이터에 값이 0이고 폭이 1인 패딩을 적용하면 입력의 크기가 (6, 6)이 된다.

- 만약, 패딩을 2, 3, .... 으로 설정한다면, 1 패딩은 입력 데이터의 각각의 원소 외각에 1 픽셀이 추가되는 것이므로 패딩이 2이면 (4, 4) 크기의 입력 데이터는 크기 (8, 8), 3으로 설정하면 크기 (10, 10)으로 확장된다.
■ 패딩 1을 추가한 입력 데이터에 동일한 합성곱 연산을 적용하면 다음과 같이 출력 데이터의 크기가 (4, 4)로 입력 크기 그대로 유지되는 것을 볼 수 있다.

■ 이렇게 패딩을 적용하면 합성곱 연산을 해도 입력 데이터의 크기 그대로 유지시켜 다음 계층에 데이터를 전달할 수 있다.
■ 위의 합성곱 연산 예시에서 필터를 적용할 때, 일정 간격만큼 순회하면서 입력 데이터와 합성곱 연산을 진행했다. 이 일정 간격을 '스트라이드'라고 한다.


■ 설정한 스트라이드 값에 따라 출력 데이터의 크기가 달라진다.
- 스트라이드를 1로 설정하면 원본 이미지와 비슷하지만,
- 스트라이드를 2로 설정하면 크기는 1/2, 면적으로는 1/4가 줄어들고
- 스트라이드를 3으로 설정하면 크기는 1/3, 면적으로는 1/9가 줄어든다.
- 스트라이드를 2로 설정하면 행 & 열 모두 2 칸씩 이동하고 3으로 설정하면 3 칸씩 이동하기 때문이다.
■ 이렇게 출력 데이터의 크기는 입력 데이터의 크기, 필터 크기, 패딩, 스트라이드에 영향을 받는다.
■ 입력 크기를 \( (H, W) \), 필터 크기를 \( (FH, FW) \), 출력 크기를 \( (OH, OW) \), 패딩을 \( P \), 스트라이드를 \( S \)라고 했을 때, 출력 크기 \( OH \)와 \( OW \)의 수식은 다음과 같다.\[
OH = \dfrac{H + 2P - FH}{S} + 1
\] \[ OW = \dfrac{W + 2P - FW}{S} + 1 \]
■ 예를 들어 입력 크기 (4, 4), 필터 (3, 3), 패딩 0, 스트라이드 1이면, \( OH = \dfrac{4 + 2 \cdot 0 - 3}{1} + 1 = 2, \quad OW = \dfrac{4 + 2 \cdot 0 - 3}{1} + 1 = 2 \)가 되므로 출력 크기는 (2, 2)
- 만약, 패딩이 1 이라면, \( OH = \dfrac{4 + 2 \cdot 1 - 3}{1} + 1 = 4, \quad OW = \dfrac{4 + 2 \cdot 1 - 3}{1} + 1 = 4 \)가 되므로 출력 크기는 (4, 4)
■ 주의할 점은 \( OH \)와 \( OW \)는 원소의 개수이므로 \( OH = \dfrac{H + 2P - FH}{S} \) 값과 \( OW = \dfrac{W + 2P - FW}{S} \) 값이 정수가 되야 한다는 점이다.
1.2.3 3차원 데이터의 합성곱 연산
■ 입력 데이터가 \( n \) 개의 채널을 갖는다면 필터의 채널 수도 \( n \) 개여야 한다.
■ 필터가 각 채널을 순회하며 합성곱 연산을 하면 채널별 특징 맵이 만들어지고, 각 채널의 피처 맵을 합산해서 최종 피처 맵인 출력 데이터(output feature map)로 반환한다.
■ 예를 들어 다음과 같은 (3, 3, 3) 형상의 입력 데이터가 있을 때, 합성곱 연산의 결과는 다음과 같다.


- 이 출력 데이터를 얻기 위해 사용해야 하는 필터의 개수는 입력 데이터의 채널 수 3 \( \times \) 출력 데이터의 채널 수 1 = 3으로 생각할 수 있다.
- 완전연결 계층에서 이 연산을 수행하려면 입력의 형상이 (3, 4, 4) 이므로 \( 3 \times 4 \times 4 = 48 \), 즉 완전연결 계층의 첫 번째 층에 노드가 48개, 출력 형상은 (1, 2, 2) 이므로 노드가 4개 필요하다.
- 완전연결 계층은 각 층마다 모든 네트워크가 연결되어 있으므로 \( 48 \times 4 = 192 \) 개의 가중치 매개변수가 필요하다.
- 이 예에서 가중치 역할을 하는 필터의 형상은 (3, 3, 3) 1개였다. 즉 가중치 역할을 하는 필터 \( 3 \times 3 \times 3 \times 1 = 27 \) 개의 파라미터만 있어도 동일한 출력 데이터를 얻을 수 있다는 것이다.
- FCN이 CNN에 비해 연산도 비효율적이며, 평탄화를 하기 때문에 3차원 공간 정보가 손실되므로, 이러한 점에서 FCN을 통해 이미지의 특징을 추출하지 않고, 비교적 효율적인 연산과 공간 정보도 챙길 수 있는 CNN을 사용하는 것이다.
■ 3차원 입력 데이터의 채널, 높이, 너비 그리고 필터의 채널, 높이, 너비로 구성되므로 하나의 직육면체 블록으로 볼 수 있다.

■ 위의 그림은 형상이 \( (C, FH, FW) \)인 필터 1 개만 사용하여 출력 결과의 형상이 \( (1, OH, OW) \)인 한 장의 피처 맵(= 채널이 1개인 피처 맵)이다.
■ 따라서 다수의 채널을 가진 피처 맵을 만들려면 다음과 같이 형상이 \( (C, FH, FW) \)인 다수의 필터를 사용하면 된다.
■ 이때의 필터 형상은 \( (FN, C, FH, FW) \), ( 출력 채널의 수, 입력 채널의 수, 필터의 높이, 필터의 너비 )로 4차원 데이터이다.

- 이때, 필요한 필터의 개수는 입력 데이터의 채널 수 C \( \times \) 출력 데이터의 채널 수 FN = C \( \times \) FN이다. 위의 그림을 보면 입력 데이터 (C, H, W)로부터 출력 데이터 (FN, OH, OW)를 계산하기 위해 채널의 수가 C인 필터가 FN개 필요한 것을 알 수 있다.
■ 여기에 형상이 \( (FN, 1, 1) \)인 편향을 더하게 되면

■ 형상이 \( (FN, 1, 1) \)인 편향의 각 값은 형상이 \( (FN, OH, OW) \)인 합성곱 계산 결과 직육면체에 대응되는 채널의 원소 모두에 더해진다.
■ \( (FN, 1, 1) \)과 \( (FN, OH, OW) \), 이렇게 형상이 서로 다른 직육면체의 덧셈은 브로드캐스팅 연산을 통해 계산할 수 있다.
1.2.4 배치 처리
■ 합성곱 연산의 배치 처리는 먼저 각 계층의 데이터를 4차원 데이터로 차원을 하나 올린다.
- 3차원 (채널 수, 높이, 너비)에 데이터 수를 추가해 4차원 (데이터 수, 채널 수, 높이, 너비)로 차원을 올린다.
■ 예를 들어 데이터가 \( N \) 개라면, 각 계층의 데이터의 흐름은 다음과 같다.

■ 이렇게 배치 처리를 하면 처리 효율이 높아진다. 4차원 데이터가 하나 들어왔을 때, 데이터 \( N \) 개에 대한 합성곱 연산을 수행하기 때문이다.
■ 배치 처리를 하지 않았다면 \( N \) 회 수행을 했겠지만, 배치 처리를 함으로써 \( N \) 회 분의 처리를 한 번에 수행할 수 있게 된 것이다.
1.3 풀링 계층(Pooling Layer)
■ 풀링 계층은 합성곱 계층의 출력을 입력으로 받아서 합성곱 계층의 출력 데이터의 크기를 줄여 계산 속도를 높이거나 필터를 키우는 효과를 이용해 각각 다른 크기의 특징을 추출하기 위해 사용한다.

■ 예를 들어 다음과 같은 고양이 이미지가 있을 때, 동일한 크기의 특징만 추출하면 다른 특징과 구별하기 힘들다.

따라서 풀링을 통해 큰 크기의 특징, 중간 크기의 특징, 작은 크기의 특징, ... 이렇게 크기가 다른 특징, 귀, 입, 눈 등을 추출한다.

■ 풀링의 유형은 최대 풀링(max pooling), 평균 풀링(average polling) 등이 있으며, 주로 최대 풀링이 쓰인다.
■ 예를 들어 다음과 같은 피처 맵에 \( 2 \times 2 \) 최대 풀링을 적용하면
(* 풀링의 크기와 스트라이드는 일반적으로 같은 값으로 설정한다.)

■ 이렇게 최대 풀링은 설정한 영역에서 가장 큰 원소를 하나 선택한다.
■ 평균 폴링은 다음과 같이 설정한 영역의 원소들의 평균값을 계산한다.

■ 풀링 계층은 이렇게 최댓값이나 평균값을 구하는 계층으로 합성곱 계층과 달리 필터 같은 학습해야 할 매개변수가 없다.
■ 또한 최댓값, 평균값 계산을 채널마다 독립적으로 계산하기 때문에 입력 데이터의 채널 수 그대로 출력 데이터로 내보낸다.
■ 예를 들어 입력 데이터의 크기가 (3, 6, 6)이면 최대 풀링 또는 평균 풀링 계산을 통해 나오는 채널의 수는 3이다.
■ 그리고 스트라이드 만큼의 영역에 대해 풀링 계산을 하기 때문에 입력 데이터의 변화에 영향을 적게 받는다.
■ 예를 들어 위의 최대 풀링 예시에서 사용한 입력 데이터의 원소를 오른쪽으로 1 칸씩 이동시켰을 때, 최대 풀링을 수행하면 다음과 같이 입력 데이터가 변화해도 거의 동일한 출력 결과가 나오는 것을 볼 수 있다.

- 단, 데이터에 따라 이렇게 거의 동일하거나 완전히 동일한 출력 결과가 나올 수도 있고, 그렇지 않을 수도 있다.
2. \( 1 \times 1 \) 합성곱
■ \( 1 \times 1 \) 필터를 생각해보자. \( 1 \times 1 \) 필터를 입력 데이터에 적용한다면, 다른 크기의 필터들과 달리 겹치는 영역이 발생하지 않는다. 즉, 이웃 픽셀에 영향을 미치지 않는다.
■ \( 1 \times 1 \) 합성곱은 원본 이미지(입력 데이터)에 \( 1 \times 1 \) 필터로 \( 1 \times 1 \) 합성곱을 하면 합성곱 과정에서 이웃 픽셀에 영향을 미치지 않으므로, 계산된 출력 데이터의 채널 수가 감소하더라도(혹은 증가하더라도) 출력 데이터는 입력 데이터와 비슷한 이미지, 즉 비슷한 특징을 갖게 된다. 이는 연산량을 줄이기 위한 일종의 테크닉으로 볼 수 있다.
■ 먼저, 연산량을 구하는 방법을 알아야 한다. 예를 들어 다음과 같이 stride = 1, pad = 0일 때 입력 (3, 6, 6)과 필터 (3, 3)으로 출력 (2, 4, 4)를 만드는데 필요한 연산량은

- 필터(커널)의 크기는 \이다. 이 크기만큼 입력 데이터에 합성곱 계산을 해서 다음과 같이 출력 데이터의 한 점(region feature)을 만든다. \( \rightarrow \boldsymbol{3 \times 3} \)

- 출력의 한 면이 \( 4 \times 4 \)이므로 이런 점들을 \( 4 \times 4 \)만큼 만들어야 한다. 즉, 출력의 크기만큼 만들어야 한다. \( \rightarrow 3 \times 3 \times \boldsymbol{4 \times 4} \)
- 이때, 입력의 채널이 3개 있으므로 위와 같은 과정을 3번 해야 출력 데이터 채널 1개가 만들어 지는 것이다. \( \rightarrow 3 \times 3 \times 4 \times 4 \times \boldsymbol{3} \)
- 예시에서 출력 데이터의 채널은 2 개이므로 지금까지의 과정을 한 번 더 해야 한다. 즉, \( 3 \times 3 \times 4 \times 4 \times 3 \)에 채널의 수 \( 2 \)까지 곱해야 (2, 4, 4) 형상의 출력 데이터가 만들어지는 것이다.
- 즉 \( 3 \times 3 \times 4 \times 4 \times 3 \times \boldsymbol{2} = 864\)가 (2, 4, 4) 형상의 출력 데이터를 만들기까지 필요한 매개변수이며, 이를 비용의 관점에서 생각하면 연산량이다.
■ 이렇게 합성곱으로 하나의 출력 데이터를 만들기까지 연산량을 수식으로 나타낸다면 다음과 같다. \[ \begin{align*}
\text{합성곱 연산량} &= \text{필터의 크기} \times \text{출력 데이터의 크기} \times \text{입력 데이터의 채널 수} \times \text{출력 데이터의 채널 수} \\
&= \text{필터의 높이} \times \text{필터의 너비} \times \text{출력 데이터의 높이} \times \text{출력 데이터의 너비} \times \text{입력 데이터의 채널 수} \times \text{출력 데이터의 채널 수}
\end{align*} \]
■ 이제 \( 1 \times 1 \) 합성곱의 예시를 보자. 예를 들어 다음과 같은 형상의 입력 데이터에 \( 1 \times 1 \) 합성곱을 진행했을 때 stride = 1이고 pad = 0 이면

연산량은 \( 1 \times 1 \times 6 \times 6 \times 5 \times 2 = 360 \)이다.
■ 만약 필터의 크기가 1보다 크다면 당연히 연산량은 360보다 클 것이다. 중요한 점은 이것이 아니라 \( 1 \times 1 \) 필터를 원본 이미지에 적용했기 때문에, 필터링된 출력 데이터가 원본 이미지와 유사한 특징을 가지는 이미지가 된다.
■ 따라서 \( 1 \times 1 \) 합성곱 결과로 나온 출력 데이터를 원본 이미지처럼 쓴다면 전체 CNN 구조에서 필요한 연산량은 감소할 것이며 원본 이미지를 input으로 넣은 결과와 비슷한 결과를 얻을 수 있다.
■ 예를 들어 필터 크기가 \( 5 \times 5 \)일 때, 다음과 같은 상황에서 합성곱을 진행한다면

- 연산량은 \( 5 \times 5 \times 28 \times 28 \times 192 \times 32 = 120,422,400 \) 약 1억 2천만이다.
- 이번에는 다음과 같이 conv2 layer 전에 \( 1 \times 1 \) 합성곱을 한다면

- 먼저 \( 1 \times 1 \) 합성곱 연산량은 \( 1 \times 1 \times 28 \times 28 \times 192 \times 16 = 2,408,448 \)
- 그리고 그다음 층과의 합성곱 연산량은 \( 5 \times 5 \times 28 \times 28 \times 16 \times 32 = 10,035,200 \)
- 따라서 총 연산량은 \( 2,408,448 + 10,035,200 = 12,443,648 \)
- 두 결과의 연산량을 비교하면, 바로 합성곱을 진행할 경우 연산량은 120,422,400, \( 1 \times 1 \) 합성곱을 통해 나온 데이터로 동일한 합성곱을 진행할 경우 연산량은 12,443,648으로 약 1/10 정도의 연산량이 줄어든 것을 확인할 수 있다.
■ 따라서 \( 1 \times 1 \) 합성곱을 통해 얻을 수 있는 이점은 원본 이미지와 유사한 특징을 가진 데이터를 사용하여 CNN 과정에서 더 효율적으로 CNN 구조의 목표인 이미지의 특징 추출을 할 수 있다는 것이다.
'딥러닝' 카테고리의 다른 글
| 매개변수 갱신 방법(2) (0) | 2024.11.03 |
|---|---|
| 매개변수 갱신 방법(1) (0) | 2024.11.01 |
| 오차역전파 (3) (0) | 2024.09.24 |
| 신경망 학습(2) (1) | 2024.09.13 |
| 신경망 학습(1) (1) | 2024.09.12 |



