2. 트랜스포머 아키텍처
■ 트랜스포머 아키텍처는 다음 그림과 같다.

2.2 어텐션(Attention)
■ 트랜스포머에서 사용되는 세 가지의 어텐션은 Encoder에서 수행되는 셀프 어텐션(Self-Attention)과 Decoder에서 수행되는 Masked Self-Attention 그리고 Encoder와 Decoder를 연결하는 부분에서의 Attention이다.

■ 이때, 각 어텐션 앞에 "Multi-head"라는 이름이 붙어있는데, 이는 한 번에 하나의 어텐션 연산만 수행하는 게 아니라 여러 어텐션 연산을 병렬적으로 동시에 수행하는 것을 의미한다.
■ 논문에는 아래의 그림과 같이 Scaled Dot-Product Attention과 Multi-Head Attention이 소개되는데, 왼쪽의 Scaled Dot-Product Attention은 하나의 어텐션 연산을 수행하는 어텐션이고, 오른쪽의 Multi-Head Attention은 헤드의 수인 h만큼 동시에 어텐션 연산을 수행하는 멀티 헤드 어텐션이다.

2.3 인코더(Encoder) 구조
■ 인코더의 구조는 다음과 같다.

■ 위와 같은 하나의 인코더를 하나의 층(layer)으로 생각하고, 하이퍼파라미터인 num_layeres 개수만큼의 인코더 층을 쌓는다. 즉, 인코더 블록을 만드는 것이다.
■ 이 인코더 구조를 하나의 계층이라고 생각한다면, 하나의 인코더 층에는 "셀프 어텐션"과 "피드 포워드" 2개의 서브 층(sub-layer)으로 나뉘어진다.
2.3.1 인코더의 첫 번째 서브 층: 셀프 어텐션(Self Attention)
■ 어텐션 함수(Attention function)는 Query와 Key-Value 쌍의 세트로 Attention Value(context vector)라는 output을 계산한다.
■ query에 대해 모든 key와의 유사도(어텐션 스코어)를 각각 구한다음, 유사도를 가중치로 만들어 각각의 key에 맵핑되어있는 value에 적용하고, 유사도가 반영된 value를 가중합하여 계산하였다.
■ 이때, Additive Attention이라 불리는 바다나우 어텐션에서 query는 \( t-1 \) 시점의 디코더의 은닉 상태, Dot-Product Attention에서의 query는 \( t \) 시점의 디코더 은닉 상태였으며, key와 value는 모두 모든 시점의 인코더 은닉 상태들이었다.
- 여기서 query, key, value 그리고 어텐션 함수의 결과인 output(context vector 또는 attention value)은 모두 벡터이다.
■ 이렇게 기존의 어텐션에서는 유사도를 계산하기 위해 사용되는 query와 key가 서로 다른 벡터였지만, 셀프 어텐션에서는 query, key, value가 전부 동일하다.
■ 트랜스포머의 셀프 어텐션에서 query, key, value는 모두 "입력 문장의 모든 단어 벡터들"이다.
■ 그래서 셀프 어텐션을 사용하면, 입력 시퀀스(ex: 문장) 내 모든 단어 쌍 사이의 관계가 계산되므로, 각 단어가 입력 문장 내에서 어떤 역할을 하는지, 어떻게 상호작용하는지 파악할 수 있다.
■ 즉, 입력 문장이 복잡한 관계를 가지더라도 문맥의 의미를 잘 이해할 수 있을 것이라 기대할 수 있다.
■ 예를 들어, 다음 그림과 같은 영어 입력 문장을 프랑스어를 번역한다고 하자.

■ 'The animal didn't cross the street because it was too tired.'라는 문장을 보면, 사람은 'it'이 'animal'을 가리킨다는 것을 알 수 있지만, 컴퓨터가 'it'이 'animal'인지 'street'인지 맞추는 작업은 다소 어려운 문제이다.
■ 하지만 query, key, value가 모두 "입력 문장의 모든 단어 벡터들"인 셀프 어텐션을 사용하면, 'The animal didn't cross the street because it was too tired.' 문장 내의 단어들끼리의 유사도를 계산하므로, 'it'이 'animal'의 관계를 찾아낼 수 있다.
2.3.1.1 query, key, value 벡터 얻기
■ 셀프 어텐션에서 query, key, value 벡터는 차원이 \( d_{models} =512 \)인 단어 벡터들보다 더 작은 차원을 가진다. query, key, value 벡터의 차원은 \( d_{models} \)의 값을 num_heads로 나눈 값으로 사용한다.
- 논문에서는 num_heads = 8로 설정하였다.
- 트랜스포머에서는 여러 어텐션을 동시에 연산하기 위해 여러 개로 분할해서 병렬로 어텐션을 수행한다. 이때 병렬의 개수가 num_heads이다.
■ 예를 들어, 'student'라는 토큰 임베딩 벡터를 query, key, value 벡터를 얻는 과정은 다음 그림과 같이 기존의 단어 벡터에 각각의 가중치 행렬을 곱하여 계산한다.

■ 위의 그림처럼 가중치 행렬을 사용하지 않고, 다음 그림과 같이 query와 key의 유사도를 계산하고, 유사도를 가중치로 변환하여 가중합을 하는 방식은 두 가지 문제가 발생할 수 있다.

■ 예를 들어, 위 그림에서 query가 'student'의 토큰 임베딩 벡터이고 key들이 'I', 'am', 'a', 'student'의 토큰 임베딩 벡터일 때, 같은 단어(예: query의 'student'와 key의 'student')끼리는 임베딩 벡터가 동일하므로 Dot-Product Attention 메커니즘을 사용한다면, 동일한 토큰 간의 유사도(어텐션 스코어) 계산 시, 유사도 값이 매우 커지게 된다.
■ 즉, 동일 단어에 대한 어텐션 스코어가 다른 단어들과의 어텐션 스코어에 비해 압도적으로 높아지면서, 'student' 토큰에 대한 어텐션 가중치가 대부분을 차지하게 되어 주변 맥락(주변 단어들)을 충분히 반영하지 못하는 결과를 초래할 수 있다.
■ 또한, 토큰 간 의미가 유사하거나 반대되는 경우에는 직접적인 관련성을 잘 포착할 수 있지만, 문법적인 구조에 의해 토큰이 연결되는 경우처럼 간접적인 관련성은 반영되기 어려울 수 있다.
■ 예를 들어, 'I am a student' 문장에서 'I'와 'am", 'a'와 'student'는 문법 관계로 연결되지만, 토큰 간의 관계가 서로 유사하거나 반대되는 경우가 아니므로 관련성을 포착하기 어렵다.
■ 트랜스포머에서는 이런 문제를 피하기 위해 2.3.1.1의 첫 번째 그림처럼 토큰 임베딩을 변환하는 가중치 \( W_q, W_k \)를 사용한다.
■ 딥러닝에서 가중치를 도입하는 이유는 무작위나 특정 분포로 초기화된 가중치들을 시작으로, 학습 과정에서 학습 데이터로 예측하고, 그 예측이 얼마나 틀렸는지 손실을 계산한 뒤, 그 오차를 줄이는 방향으로 가중치 값들을 업테이트해서 올바른 관계를 얻기 위함이다.
■ 즉, 가중치 행렬 \( W_q, W_k \)를 사용하는 이유는 토큰과 토큰 사이의 관계를 계산하는 능력을 학습시키기 위함이다.
■ value 벡터도 토큰 임베딩을 가중치 행렬 \( W_v \)를 통해 변환한다.
■ 이렇게 트랜스포머에서는 \( W_q, W_k, W_v \) 가중치 행렬을 통해 토큰과 토큰 사이의 관계를 계산해서 적절히 주변 맥락을 반영하는 방법으로 학습한다.
2.3.1.2 스케일드 닷-프로덕트 어텐션(Scaled Dot-Product Attention)
■ query, key, value 벡터를 얻었다면 어텐션 메커니즘을 통해 query 벡터는 모든 key 벡터들에 대해서 어텐션 스코어를 계산하고, Softmax function을 거쳐 어텐션 분포(어텐션 가중치)를 구한 다음, 어텐션 가중치를 모든 value 벡터에 가중합하여 output 벡터(context vector, attention value)를 구하게 된다. 그리고 이 과정을 모든 query 벡터에 대해서 반복한다.
■ 논문에서는 어텐션 메커니즘으로 아래의 그림과 같은 구조를 가지는 "스케일드 닷-프로덕트 어텐션" 함수를 사용한다.


■ 논문에서는 query와 key 벡터의 차원은 \( d_k \), value 벡터의 차원은 \( d_v \)라고 할 때, \( \sqrt{d_k} \)를 query와 모든 key들의 dot-product를 계산한 결과에 각각 나눈 후, Softmax function을 통해 value에 대한 가중치를 계산한다고 설명하고 있다.
- \( d_k = d_{models} / \text{num_heads} \)의 값을 이용하였다.
■ 이때, 스케일드 닷-프로덕트 어텐션 함수의 입력으로 들어가는 Q, K, V는 여러 query, key, value 벡터들로 묶은 행렬 Q, K, V이다. 행렬 연산을 사용하면 일괄 계산이 가능하기 때문이다.
■ 논문에 따르면, Additive attention(바다나우 어텐션)과 Dot-product attention을 비교했을 때, 두 알고리즘은 이론적인 복잡도 측면에서 유사하지만, 실제로는 Dot-product attention이 행렬 곱 연산을 사용하기 때문에 Additive attention보다 훨씬 빠르고 공간 효율적이라고 설명한다. 행렬로 일괄 계산하기 때문이다.
■ 이때, \( d_k \)의 값이 작은 경우 두 메커니즘(additive attention과 dot product attention)은 비슷한 성능을 보이나, 더 큰 \( d_k \) 값을 스케일링 없이 사용하면, additive attention의 성능이 dot product attention보다 더 우수한 성능을 보였다고 한다.
■ 저자들은 이러한 결과의 원인이 query와 key 벡터의 차원 값인 \( d_k \)의 값이 크면, query 벡터와 key 벡터의 dot product의 결과가 Softmax function을 극도로 작은 기울기를 갖는 영역으로 밀려나게 하는 것으로 추측하였다.
■ 그래서 이 효과를 상쇄하기 위해 dot product에 \( \dfrac{1}{\sqrt{d_k}} \)로 스케일링을 적용하였다고 설명한다.
■ \( \text{softmax} \left( q \cdot k^T \right) \)를 생각해보자. 예를 들어, \( q \cdot k^T \) dot product의 결과로 [1, 2, 100]이 나왔다고 가정하자.
■ 그렇다면, [1, 2, 100]은 Softmax function의 입력값으로 들어가게 된다. 입력값들을 받아 확률 분포를 반환하는 Softmax는 \( \sigma(x_j) = \dfrac{e^{x_j}}{\displaystyle\sum_{i=1}^n e^{x_i}} \)으로 식에 exp()가 포함되어 있어 입력값들 간의 상대적인 차이에 민감하다.
■ [1, 2, 100]처럼 입력값들 간의 상대적인 차이가 큰 경우, Softmax function의 결과는 세 번째 값인 100을 1.0에 가까운 확률값, 첫 번째와 두 번째 값인 1과 2는 0에 가까운 확률값으로 변환될 것이다.
■ 역전파 과정에서 [1, 2, 100] \( \rightarrow \) Softmax function \( \rightarrow \) [0.000..., 0.000..., 0.999...]의 역순으로 미분을 통해 업데이트가 될 텐데
■ Softmax function의 미분은, x, y, z 3개의 변수가 있다고 가정했을 때,
- \( \sigma(x) = \dfrac{e^x}{e^x + e^y + e^z} \)에 대하여
- \( x \)로 미분하면, \( \dfrac{\partial \sigma(x)}{\partial x}
= \dfrac{e^x (e^x + e^y + e^z) - e^x \cdot e^x}{(e^x + e^y + e^z)^2}
= \dfrac{e^x (e^y + e^z)}{(e^x + e^y + e^z)^2}
= \sigma(x) \cdot (1 - \sigma(x)) \)
- \( y \)로 미분하면, \( \dfrac{\partial \sigma(x)}{\partial y}
= \dfrac{0 - e^x e^y}{(e^x + e^y + e^z)^2}
= -\dfrac{e^x}{e^x + e^y + e^z} \cdot \dfrac{e^y}{e^x + e^y + e^z}
= -\sigma(x)\sigma(y) \)
- 그러므로 \( z \)로 미분하면 \( -\sigma(x)\sigma(z) \)가 된다.
- \( \sigma(y) = \dfrac{e^y}{e^x + e^y + e^z}, \quad \sigma(z) = \dfrac{e^z}{e^x + e^y + e^z} \)에 대해서도 각각 \( x, y, z \)로 미분하면
- \( \dfrac{\partial \sigma(y)}{\partial x} = -\sigma(x)\sigma(y), \quad
\dfrac{\partial \sigma(y)}{\partial y} = \sigma(y)(1 - \sigma(y)), \quad
\dfrac{\partial \sigma(y)}{\partial z} = -\sigma(y)\sigma(z) \)
- \( \dfrac{\partial \sigma(z)}{\partial x} = -\sigma(x)\sigma(z), \quad
\dfrac{\partial \sigma(z)}{\partial y} = -\sigma(y)\sigma(z), \quad
\dfrac{\partial \sigma(z)}{\sigma z} = \sigma(z)(1 - \sigma(z)) \)가 된다.
- 정리하면 \( \begin{pmatrix}
\sigma(x)(1 - \sigma(x)) & -\sigma(x)\sigma(y) & -\sigma(x)\sigma(z) \\
-\sigma(y)\sigma(x) & \sigma(y)(1 - \sigma(y)) & -\sigma(y)\sigma(z) \\
-\sigma(z)\sigma(x) & -\sigma(z)\sigma(y) & \sigma(z)(1 - \sigma(z))
\end{pmatrix} \)
■ Softmax의 미분 값은 위와 같이 확률값들의 곱으로 표현되기 때문에 확률값들이 작을수록, 역전파 과정에서 Softmax function로부터 전달되는 gradient 값 또한 작아진다. 작은 값의 gradient가 누적되면, 기울기 소실 문제가 발생할 수 있다.
■ 정리하면, 스케일링이 없는 상황에서 query와 key 벡터의 차원이 큰 경우( \( d_k \) 값이 큰 경우) dot-product attention에서 기울기 소실 문제로 인해 additive attention보다 성능이 떨어진 것으로 볼 수 있다.
■ 이러한 문제를 해결하기 위해 논문에서는 \( \dfrac{1}{\sqrt{d_K}} \)로 내적 값을 스케일링하는 것을 제안하였다.
■ 아래의 글은 왜 스케일링을 \( \dfrac{1}{\sqrt{d_K}} \)로 사용하는지 정리한 글이다.
■ 여기서는 행렬 \( Q, \; K \)의 모든 값이 독립이며, 평균=0 & 분산=1이라고 가정했을 때, \( Q \cdot K^T \)의 한 요소(내적 값)을 본다.
- 두 벡터가 \( \mathbf{a} = (a_1, a_2, \cdots, a_{d_k} ), \; \mathbf{b} = (b_1, b_2, \cdots, b_{d_k} ) \)이면,
- \( Q \cdot K^T \)의 한 요소는 \( a_1 b_1 + a_2 b_2 + \cdots + a_{d_k} b_{d_K} \)일 것이다.
■ 평균=0 & 분산=1이라면, 기댓값과 분산은 다음과 같다.

■ 여기에 두 벡터의 차원인 \( d_k \)만큼 더해주면,

분산이 \( d_k \)가 된다.
■ 그러므로, 이 가정에서는 \( d_k \)가 커질수록 내적 계산에서 더 많은 항들이 더해지며, 내적 값의 분산은 \( d_k \) 값과 비례하여 커지게 된다.
■ 분산이 관측값에서 평균을 뺀 값을 제곱하고, 그것을 모두 더한 후 관측값들의 전체 개수로 나눈 값이므로, 평균이 0인데 분산이 커진다는 것은 관측값인 내적 값이 0에서 더 멀리 떨어진 큰 양수 값과 작은 음수 값(절댓값이 큰 값)을 가질 가능성이 높아진다는 의미가 된다.
■ 이러한 관측치들을 Softmax function에 넣는다고 생각해보자. Softmax 는 입력값들의 상대적인 차이에 민감하기 때문에 위의 Softmax 예시처럼 Softmax function의 출력은 거의 [0, 0, 1]에 가까운 분포가 된다.
■ 즉, 첫 번째와 두 번째 값은 아래의 Softmax 그래프에서 왼쪽 끝 부분인 평평한 부분에 세 번째 같은 값은 오른쪽 끝 부분인 평평한 부분에 위치하게 될 것이다.

■ 즉, Softmax의 결과는 입력값들의 상대적 차이가 클수록 평평한 부분에 위치할 가능성이 높아지며, 이러한 영역에서는 위의 그래프에서 확인할 수 있듯이 기울기가 0 또는 0에 매우 가까운 값을 가지게 된다.
■ 평평한 영역 위에서는 어느 방향으로 움직여도 높이 변화가 거의 없어서 어디로 가야 하는지 알기 어려운 상황이라고 볼 수 있다. 즉, 앞서 말한 기울기 소실 문제가 발생할 수 있다.
■ 실제로, 소프트맥스 함수 미분은 위에 적은 것처럼 \( \sigma'(x) = \sigma(x) \left( 1 - \sigma(x) \right) \)이므로, \( x \)가 위 예시의 첫 번째, 두 번째 확률값처럼 0에 가까운 값이면, \( \sigma'(x) \). 즉, Softmax의 gradient 값도 0에 가까운 값이 되며, 세 번째 확률값처럼 1에 가까운 값이어도 Softmax의 gradient 값은 0에 가까운 값이 된다.
■ 만약, 위의 분산 \( \text{Var} \left( Q \cdot K^T \right) = d_k \)에서 \( \sqrt{d_k} \)를 나누면 어떻게 될까. 즉, \( \text{Var} \left( Q \cdot K^T \right) \)에서 \( \text{Var} \left( \dfrac{Q \cdot K^T}{\sqrt{d_K}} \right) \)를 한다면?, \( d_k \)는 숫자 값이다.
■ 즉, 분산 성질에 의해 \( \text{Var} \left( c x \right) = c^2 \text{Var} \left( x \right) \) ( \( c \)는 상수 ), 이므로 \( \text{Var} \left( \dfrac{Q \cdot K^T}{\sqrt{d_K}} \right) = \text{Var} \left( Q \cdot K^T \right) \cdot \left( \dfrac{1}{\sqrt{d_k}} \right)^2 = d_k \cdot \dfrac{1}{d_k} = 1 \)이 된다.
■ 이렇게 \( \sqrt{d_k} \)로 나누면 분산이 1이 된다. 평균이 0이고 분산이 1이면, 이전처럼 분산이 \( d_k \)에 비례하지 않는다.
■ 즉, \( \sqrt{d_k} \)를 사용하는 것은 Softmax의 입력이 극단적인 분포를 가지지 않도록 조정함으로써, 역전파 과정에서 Softmax의 미분으로 인해 발생할 수 있는 기울기 소실 문제를 완화할 수 있다.
■ 예를 들어, 'I am a student'라는 문장의 단어 벡터에 각각 가중치 행렬 \( W_q, W_k, W_v \)를 곱하여 Q, K, V 행렬을 구한 뒤, 이를 스케일드 닷-프로덕트 어텐션으로 어텐션 값을 계산하는 과정을 나타내면,
■ 먼저 아래 그림처럼 단어 벡터에 대해 각각 가중치 행렬 \( W_q, W_k, W_v \)를 곱하여 Q, K, V 행렬을 구한 다음,

■ 스케일드 닷 어텐션 함수로 유사도(어텐션 스코어)를 계산한다.



■ \( Q \)와 \( K^T \)의 행렬 곱 연산을 수행하면, query 벡터와 key 벡터의 내적이 각 행렬의 원소가 되는 행렬이 결과로 나오게 된다. 이 결과 행렬에 \( \sqrt{d_k} \)로 스케일링을 적용하면 각 행과 열이 어텐션 스코어 값을 나타내는 행렬이 된다.
- 예를 들어, 'I' 행과 'student' 열의 값은 'I'의 query 벡터와 'student'의 key 벡터의 어텐션 스코어 값이다.
■ 결과 행렬을 Softmax에 통과시켜 어텐션 분포를 구한 다음, 이를 value 벡터의 집합인 \( V \)행렬에 곱하여 어텐션 값을 계산한다.
■ 입력 문장의 길이를 seq_len이라고 한다면, 문장 행렬의 크기는 (seq_len, \( d_{model} \))이다. 여기에 \( W_q, W_k, W_v \) 가중치 행렬을 각각 곱해 \( Q, \; K, \; V \) 행렬을 만든다.
■ 이때, query 벡터와 key 벡터의 차원은 \( d_k \), value 벡터의 차원은 \( d_v \)이며, 문장 행렬과 곱해져야 하므로 \( W_q \)와 \( W_k \)의 크기는 \( (d_{model}, d_k) \), \( W_v \)의 크기는 \( (d_{model}, d_v) \)가 되어야 한다.
■ 그러면, \( Q \)와 \( K \)의 크기는 (seq_len, \( d_{k} \)), \( V \)의 크기는 (seq_len, \( d_{v} \))가 된다.
- \( h \)는 num_heads
■ 그러므로, 스케일드 닷-프로덕트 어텐션 함수를 적용하여 나오는 어텐션 값 행렬의 크기는 (seq_len, \( d_v \))라고 할 수 있다.
■ 이 과정을 다음과 같이 구현할 수 있다.
input_text = "I am a student"
word_list = input_text.lower().split()
word_list
```#결과#```
['i', 'am', 'a', 'student']
````````````from collections import Counter
word_counts = Counter(word_list)
vocab = sorted(word_counts, key=word_counts.get, reverse=True)
word2idx = {}
for index, word in enumerate(vocab):
word2idx[word] = index
word2idx
```#결과#```
{'i': 0, 'am': 1, 'a': 2, 'student': 3}
````````````
token_ids = {word2idx[word] for word in word_list} # 'the'의 정수 인덱스 중복 방지
token_ids
```#결과#```
{0, 1, 2, 3}
````````````import torch
import torch.nn as nn
embedding_dim = 16
embedding_layer = nn.Embedding(len(word2idx), embedding_dim)
token_ids = list(token_ids)
input_embeddings = embedding_layer(torch.tensor(token_ids))
# input_embeddings.shape: (4, 16)
input_embeddings = input_embeddings.unsqueeze(0)
# input_embeddings.shape: (1, 4, 16)■ 파이토치의 torch.nn.Linear()를 사용하여 쿼리, 키, 값에 대한 각각의 가중치를 생성할 수 있다.
head_dim = 16
# 가중치
W_q = nn.Linear(embedding_dim, head_dim)
W_k = nn.Linear(embedding_dim, head_dim)
W_v = nn.Linear(embedding_dim, head_dim)■ 그리고 생성한 선형 층(가중치)에 단어의 임베딩 벡터를 통과시켜, 다음과 같이 \( Q, \;, K, \; V \)를 생성한다.
querys = W_q(input_embeddings)
keys = W_k(input_embeddings)
values = W_v(input_embeddings)
querys.shape, keys.shape, values.shape
```#결과#```
(torch.Size([1, 4, 16]), torch.Size([1, 4, 16]), torch.Size([1, 4, 16]))
````````````■ 아래의 함수는 스케일드 닷-프로덕트 어텐션 함수를 수행한다.
from math import sqrt
import torch.nn.functional as F
def scaled_dot_product_attention(querys, keys, values):
dim_k = querys.size(-1) # 16
scores = querys @ keys.transpose(1, -1) / sqrt(dim_k)
weights = F.softmax(scores, dim=-1)
return weights @ values
result = scaled_dot_product_attention(querys, keys, values)
print(input_embeddings.shape)
print(result.shape)
```#결과#```
torch.Size([1, 4, 16])
torch.Size([1, 4, 16])
````````````■ 단계별로 설명하면,
- 유사도(scores)를 계산하기 위해 쿼리와 키를 곱하고 분산이 커지는 것을 방지하기 위해 query, key의 차원 수(dim_k)의 제곱근으로 나눠준다.
- 그다음, 어텐션 가중치(weights)를 계산하기 위해 유사도를 Softmax function에 통과시킨다.
- 마지막으로 가중치와 값의 곱을 통해 결과를 반환한다.
■ 이 셀프 어텐션 과정에서 반환되는 결과는 가중치와 값을 곱한 후 더해서 주변 단어의 맥락을 반영한 하나의 value의 임베딩으로 만든다. 이 과정에서 가중치 값이 가장 큰 것이 가장 많은 비중으로 섞이게 된다.



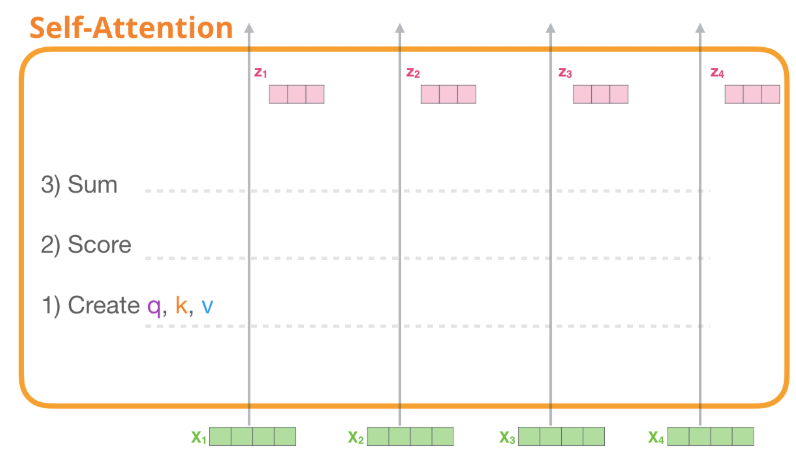
- 먼저 가중치 행렬 \( W_q, W_k, W_v \)를 입력 벡터 \( x_1, x_2, x_3, x_4 \)와 곱해서 query, key, value 벡터를 계산한다.
- 위의 그림에서는 첫 번째 query 벡터 q1을 기준으로, 모든 key 벡터와의 연산을 통해 유사도(어텐션 스코어)를 계산한 다음, 소프트맥스 함수에 유사도를 통과시켜 가중치로 변환한다.
- 그리고 가중치들을 value 벡터인 \( v_1, v_2, v_3, v_4 \)에 각각 곱한 후, 모두 더해서 \( z_1 \)을 계산한다. \( v_3 \)은 가중치가 0.5로 가장 크기 때문에 가장 많은 비중으로 섞이고, \( v_w \)는 가중치라 0.1로 가장 작기 때문에 가장 적은 비중으로 섞이게 된다.
- 이 과정을 \( x_2, x_3, x_4 \)에 대해서도 동일하게 반복하여 나머지 \( z_2, z_3, z_4 \)를 계산한다.
■ 위와 같은 셀프 어텐션 과정을 거치고 나면, 주변 단어(토큰)과의 관련도에 따라 값 벡터를 조합한 새로운 토큰 임베딩이 생성된다.
2.3.1.3 멀티 헤드 어텐션(Multi-Head Attention)

■ 논문에 따르면, \( d_{model} \) 차원의 queries, keys, values를 사용하여 어텐션 연산을 1회 수행하는 대신, queries, keys, values을 서로 다른 학습된 선형 프로젝션(liner projection). 즉, 가중치 행렬을 통해 \( h \)(=num_heads)번 각각 \( d_k, \; d_k, \; d_v \) 차원으로 투영하는 것이 더 효과적이었다고 한다.
- 여기서 말하는 가중치 행렬은 \( W_q, \; W_k, \; W_v \)를 말한다.
■ 즉, 한 번의 어텐션을 수행하는 것보다 여러 개의 어텐션을 병렬로 수행하는 것이 더 효과적이라고 판단한 것이다.
■ 투영된 queries, keys, values에 대해 병렬적으로 어텐션 함수를 수행하여 \( d_v \) 차원의 output values를 생성한다.
- 여기서 output values는 스케일드 닷-프로덕트 어텐션으로 셀프 어텐션한 결과인 값 임베딩(attention value, context vector)을 의미한다.
■ 그리고 논문에 따르면, 이들을 연결하고 다시 투영하여 다음 그림에 묘사된 것과 같이 최종값을 생성한다고 한다.

- 여기서 투영을 위해 사용되는 행렬은 가중치 행렬 \( W_o \)이다.
■ 이러한 멀티 헤드 어텐션은 모델이 서로 다른 위치에서 서로 다른 표현 subspace의 정보에 공동으로 주의를 기울일 수 있게 한다. 각 헤드는 "독립적으로" 어텐션 계산을 수행하고, 이 과정에서 고차원의 공간에 존재하는 입력 정보를 각 헤드마다 다른 선형 변환 행렬을 통해 저차원의 subspace로 "투영"시키니, 각 헤드는 입력 정보의 서로 다른 특징을 볼 수 있는 것이다.
- 예를 들어, 한 헤드는 문법적인 관계를 파악하는 데 특화될 수 있고, 다른 헤드는 의미적인 관계를 파악하는 데 특화될 수 있다.
- 이렇게 각 헤드는 입력 벡터 공간의 서로 다른 '부분 공간'에서 의미 있는 정보를 추출하게 된다.
- 그리고 이 모든 정보를 연결하여 최종 표현을 만들고, 다시 투영시켜 최종 결과를 계산한다.
- 이러한 과정을 거치기 때문에 하나의 어텐션만 사용할 때보다 훨씬 다양한 관점에서 입력의 정보를 동시에 고려할 수 있는 것이다.
- 여기까지의 과정을 그림으로 나타내면 다음과 같다.

■ 저자들은 h = 8개의 병렬 어텐션 레이어. 즉 헤드를 사용한다. 각 헤드에 대해 \( d_{models} / h = 64 \)를 사용한다. 각 헤드의 차원이 줄어들기 때문에 총 계산 비용은 전체 차원을 사용하는 단일 헤드 어텐션과 유사하다고 한다.
■ 즉, 멀티 헤드 어텐션 메커니즘의 아이디어는 하나의 어텐션 함수를 \( d_{models} = 512 \)라는 고차원에서 수행하는 대신, queries, keys, values를 \( h \)개의 다른 '헤드(head)'로 나누어 병렬 처리하는 것이다.
- 논문에서 \( d_{models} \)의 값을 512로 설정
■ 각 헤드는 Q, K, V를 서로 다른 학습 가능한 선형 변환 \( W_q, W_k, W_v \)을 통해 더 낮은 차원 \( d_k, d_k, d_v \)로 투영된다.
- \( W_q \)와 \( W_k \)의 크기가 \( d_{models} \times d_k \), \( W_v \)의 크기가 \( d_{models} \times d_v \)이므로 \( d_k, d_k, d_v \)로 투영되는 것이다.
■ 이렇게 투영된 Q, K, V에 대해 각 헤드마다 독립적으로 어텐션 함수를 수행한다.
- 각 헤드마다 어텐션 연산하는 부분에 사용되는 가중치 행렬 \( W_q, W_k, W_v \)의 값은 어텐션 헤드마다 전부 다른 값을 가진다.
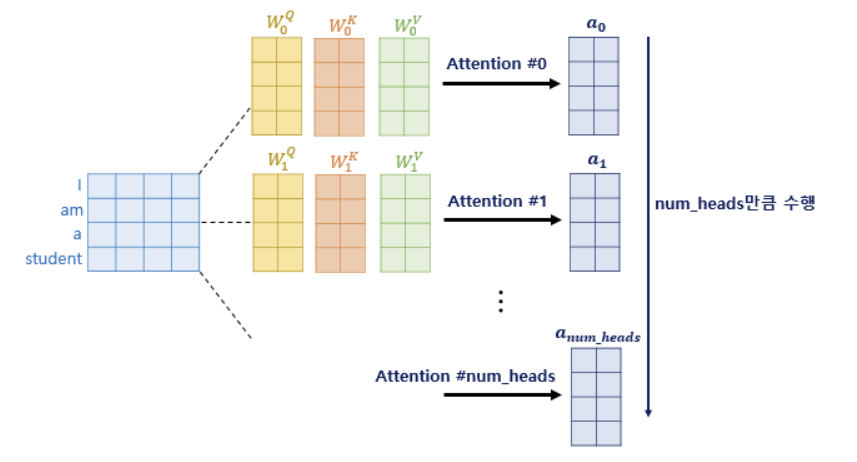
■ \( h \)개의 헤드에서 각각 나온 \( d_v \) 차원의 어텐션 출력 결과를 모두 연결(concatenate)한다. 그러므로 연결된 벡터는 차원이 \( d_v \times h = d_{models} \)가 된다.

■ 이 연결된 벡터를 다시 한번 학습 가능한 선형 변환(또는 가중치 행렬) \( W_o \)에 투영시켜 최종 출력값을 얻는다.

■ 이렇게 하면 원래 차원으로 단일 어텐션 함수 돌리는 거랑 계산 비용도 동일하고, 모델이 입력(여기서 입력은 토큰(또는 단어))의 서로 다른 위치에서 다양한 representation subspaces의 정보에 동시에 집중할 수 있게 된다.
■ 그래서 'it = animal or street" 같은 문제에서 'it'이 무엇을 가리키는지에 대해 알아낼 수 있는 것이다.
■ 예를 들어 query가 'it'이었다고 하자. 그러면 'it'에 대한 query 벡터로부터 다른 단어 벡터와의 연관도를 구했을 때, 각 어텐션 헤드는 전부 다른 시각에서 보고 있기 때문에 첫 번째 어텐션 헤드는 'it'과 'animal'의 연관도를 높게 본다면, 두 번째 어텐션 헤드는 'it'과 'tired'의 연관도를 높게 볼 수 있다. 즉, 한 헤드는 문장의 구문 구조에, 다른 헤드는 의미론적 관계에 집중할 수 있기 때문이라고 볼 수 있다.
■ 요약하자면, 멀티-헤드 어텐션은 고차원의 단어 벡터를 투영시켜 여러 개의 헤드로 나누어 어텐션을 병렬 처리해서 입력을(토큰 사이의 관계를) 여러 관점에서 동시에 바라보고, 각 관점에서 얻은 정보를 종합하여 더 다양한 특징을 학습할 수 있도록 하는 효과적인 메커니즘이다.
2.3.1.4 패딩 마스크(Padding Mask)
■ 패딩 마스크는 입력 문장에 <PAD> 토큰이 있을 경우, 어텐션에서 제외하기 위한 연산이다.
■ 예를 들어, 입력 문장에 <PAD> 토큰이 포함된 경우 셀프 어텐션을 수행했을 때, 어텐션을 수행하고 어텐션 스코어를 계산하는 과정은 다음 그림과 같다.

■ <PAD> 토큰의 벡터가 어텐션 스코어 계산에 포함되는 것을 볼 수 있다.
■ 그러나 <PAD>는 다른 단어 벡터들처럼 실질적인 의미를 갖는 단어가 아니므로, 마스킹(masking)을 적용하여 유사도(어텐션 스코어) 계산 시 <PAD>에 대한 유사도가 반영되지 않도록 해야 한다.
■ 위 그림의 어텐션 스코어 행렬에서 행은 문장의 query, 열은 문장의 key라고 하자. <PAD>가 있는 부분에 마스킹을 적용하면 된다.
■ 마스킹을 하는 방법은 마스킹할 위치에 "-무한대"에 가까운 음수값을 넣어주는 것이다.
■ 왜냐하면, 어텐션 가중치를 얻기 위해 어텐션 스코어는 소프트맥스 함수를 통과하고, 그 후 value 행렬과 곱해지게 되는데, 이때 마스킹된 위치에 매우 작은 음수 값이 있다면, 소프트맥스 함수 결과에서 해당 위치의 값은 0이 되기 때문이다.
■ 소프트맥스 함수 결과로 각 어텐션 가중치의 총합은 1.0이 되는데, 마스킹된 위치에는 0.0이 할당되므로, 실질적 의미가 있는 단어들에 대한 가중치만으로 총합이 1.0이 된다. 결과적으로 <PAD> 토큰은 어텐션 연산에 전혀 영향을 미치지 않게 된다.
2.3.2 인코더의 두 번째 서브 층: Position-wise Feed-Forward Networks
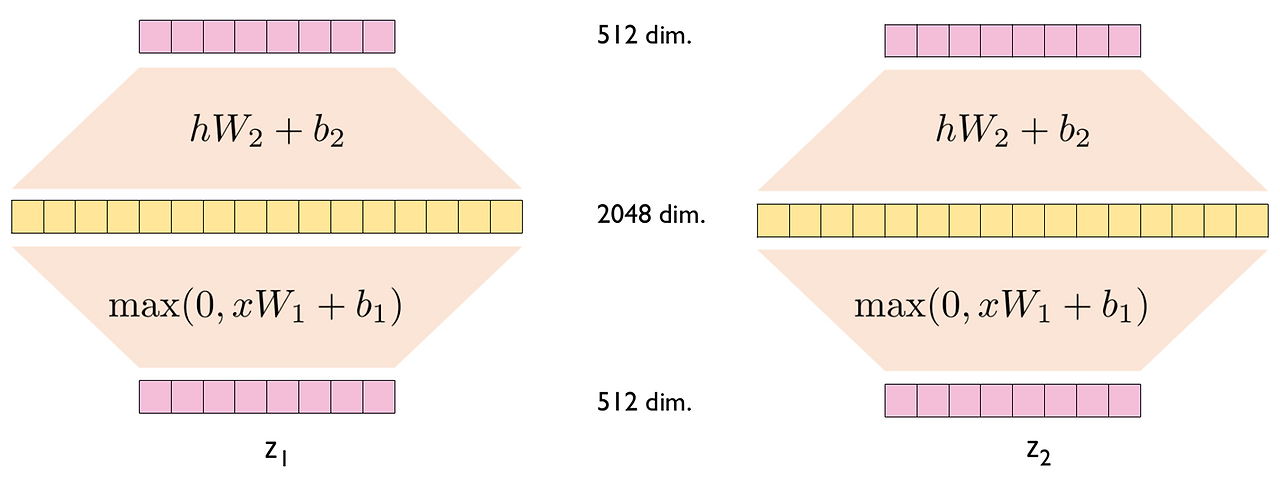
■ 포지션-와이즈 FFN은 인코더의 두 번째 서브 층(sub-layer)이기도 하지만, 인코더와 디코더에서 공통적으로 포함하고 있는 서브 층이다. 포지션-와이즈 FFN의 수식은 아래와 같다.

■ 식을 그림으로 표현하면 다음과 같다.

■ FFN은 두 개의 선형 변환(linear transformation)과 그 사이에 ReLU 활성화 함수로 구성되어 있는 것을 볼 수 있다.
■ FFN의 입력으로 들어오는 \( x \)는 인코더 기준으로, 멀티 헤드 어텐션 결과로 나온 (seq_len, \( d_{models} \))의 크기를 가지는 행렬이다.
■ 그러므로, 선형 변환을 위해 가중치 행렬 \( W_1 \)은 \( (d_{models}, d_{ff}) \)의 크기를, 가중치 행렬 \( W_2 \)는 \( (d_{ff}, d_{models}) \) 크기를 가진다.
- 논문에서는 \( d_{ff} \)의 값으로 2048을 사용했다.
■ 논문에 따르면, FFN은 각 계층마다(하나의 인코더 블록, 디코더 블록마다) 각 위치에 개별적으로 그리고 동일하게 적용된다고 한다. 즉, FFN은 FFN 내부에서 \( d_{models} = 512 \)에서 \( d_{ff} = 2048 \)로 일시적으로 차원을 확장한 다음, 선형 변환 및 ReLU 함수를 통해 비선형성을 도입하여 각 위치의 표현력(더 복잡하고 풍부한 특징)을 높이기 위한 용도로 볼 수 있다.
- \( W_1 \)을 통하여 \( d_{models} \rightarrow d_{ff} \) 으로 차원이 일시적으로 확장되었다가, \( W_2 \)를 통하여 \( d_{ff} \rightarrow d_{models} \)으로, 다시 원래의 입력/출력 차원 \( d_{models} \)으로 축소된다.
- 피드 포워드 층(feed-forward layer)은 데이터의 특징을 학습하는 완전 연결 층(fully-connected layer)을 말한다.
■ 각 계층마다 각 위치에 개별적으로 그리고 동일하게 적용된다는 의미는, 매개변수 \( W_1, \; b_1, \; W_2, \; b_2 \)가 하나의 인코더(또는 디코더) 층 내에서는 다른 문장(또는 다른 단어)들마다 동일하게 적용되지만, 매개변수 \( W_1, \; b_1, \; W_2, \; b_2 \)는 인코더(또는 디코더) 층마다 다른 값을 가진다는 얘기이다.
■ 즉, 서로 다른 인코더/디코더 계층에 있는 FFN은 서로 다른 매개변수를 가진다.
- 예를 들어 1번 인코더 계층의 FFN과 2번 인코더 계층의 FFN은 서로 다른 가중치를 사용한다.
- 단, 하나의 계층 내에서는 동일한 가중치를 적용한다.
■ 아래의 그림은 위의 내용을 도식화한 것이다.
■ 인코더 입증에서 인코더 층의 첫 번째 서브 층인 멀티 헤드 어텐션이 단어 사이의 관계를 파악하는 역할이라면, 두 번째 서브 층인 피드 포워드 층은 입력 텍스트 전체를 이해하는 역할을 한다고 볼 수 있다.
■ 아래의 그림은 1번 인코더 계층의 입력이 멀티 헤드 어텐션과 FFN을 통과해서, 그 결과가 2번 인코더 계층의 입력으로 들어가는 것을 나타내고 있다. 이렇게 바로 2번 인코더 계층으로 들어갈 수 있는 이유는 입력과 출력의 형태 (seq_len, \( d_{models} \))가 그대로 보존되고 있기 때문이다.

■ 입력과 출력의 형태(차원)를 동일하게 유지하는 이유는, 차원이 동일하게 유지되면 쉽게 인코더(또는 디코더) 층을 쌓아 확장할 수 있기 때문이다.
■ 첫 번째 인코더 계층을 통과한 출력은 다음 인코더 계층으로 전달된다. 이후의 인코더 계층에서도 동일한 인코더 연산이 반복된다.
2.4 잔차 연결(Residual Connection)과 층 정규화(Layer Normalization)
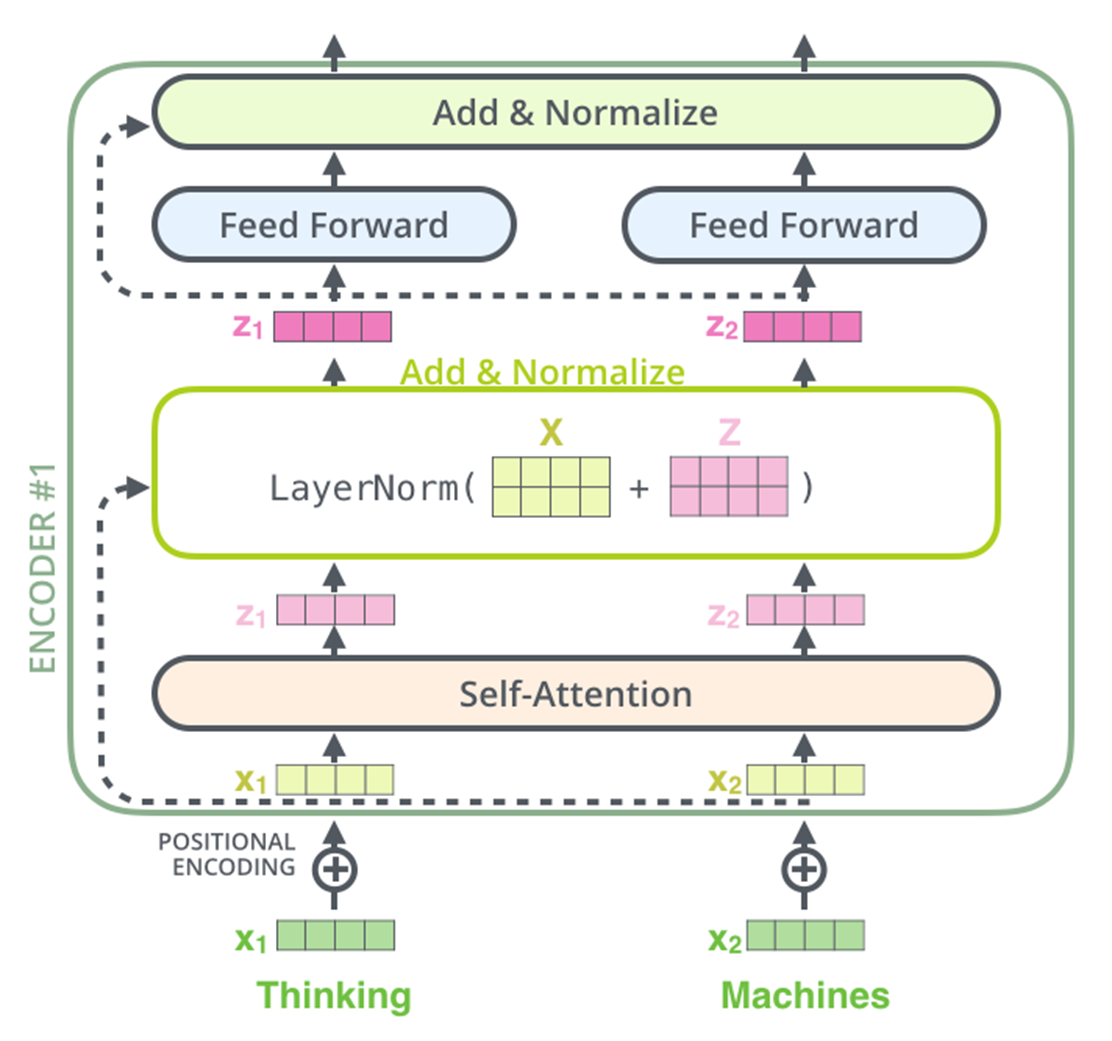
■ 인코더에는 두 개의 sub-layer(멀티 헤드 셀프 어텐션, 포인트-와이즈 피드 포워드 신경망)이 있다. 논문에 따르면 두 서브 층 각각에 잔차 연결을 사용했고, 그 뒤에는 층 정규화를 사용했다고 한다.
- 이 내용에 대한 부분이 바로 트랜스포머 아키텍처에 있는 'Add & Norm'이다.
- 2.에 있는 아키텍처를 보면, 'Add & Norm'이 각 서브 층 이전의 입력에서 시작되어 서브 층의 출력 부분으로 향하는 것을 확인할 수 있다. 논 문에서는 서브 층의 출력을 " LayerNorm(x + Sublayer(x))"으로 표현하였다.
- 여기서 Sublayer(x)는 서브 층 자체에 의해 구현된 함수이다.
■ 아래의 그림은 잔차 연결과 층 정규화를 거쳐 포인트 와이즈 피드 포워드 신경망으로 들어가는 과정을 도식화한 것이다.
2.4.1 잔차 연결
■ 아래의 skip connection 구조 그림에서 어떤 함수 \( F(x) \)가 트랜스포머에서의 서브 층에 해당된다.

■ 서브 층의 입력 \( x \) 값과 서브 층의 출력 \( F(x) \) 값이 더해지는 것을 볼 수 있다.
■ 트랜스포머에서는 입력과 출력의 차원이 \( d_{models} \)로 동일한 차원을 가지고 있으므로, 서브 층의 입력 \( x \)와 서브 층의 출력 \( F(x) \)는 덧셈 연산을 할 수 있다.
■ 이를 식으로 표현하면 \( x + \text{Sublayer}(x) \)이다. 만약, 서브 층의 입력 \( x \)가 인코더의 멀티 헤드 셀프 어텐션의 출력 결과였다면, \( H(x) = x + \text{Multi-Head Attention}(x) \)로 표현할 수 있으며, 이 \( H(x) \)는 FFN으로 전달되기 전에 층 정규화를 거치게 된다.
■ 즉, 층 정규화는 \( x + \text{Sublayer}(x) \)를 입력으로 받는 것이다.
참고) 논문에 Residual Dropout이라는 내용이 나온다, 잔차 연결 부분에서 하위 계층의 입력이 더해지고 정규화되기 전에, 드롭아웃을 적용했다는 내용이다. 그리고 인코더와 디코더 스택 모두에서 임베딩과 위치 인코딩의 합계에도 드롭아웃을 적용했으며, 기본 모델에서 드롭아웃의 비율은 0.1을 사용했다고 한다.
2.4.2 층 정규화
■ 잔차 연결을 거친 결과 \( x + \text{Sublayer}(x) \)는 이어서 층 정규화 과정을 거치게 된다. 잔차 연결과 층 정규화를 모두 거친 결과를 논문에서는 \( \text{LayerNorm}(x + \text{Sublayer}(x)) \)으로 표현했다.
■ 정규화는 딥러닝 모델에서 입력이 일정한 분포를 갖도록 만들어 학습이 안정적이고 학습 속도가 빨라질 수 있도록 하는 기법이다.
- 예를 들어, 사람의 나이와 키를 기반으로 몸무게를 예측하는 모델을 생각했을 때, 나이는 나이 단위를 기준으로 보통 1~100 사이의 값을 가진다.
- 이때, 키의 값의 단위를 cm 단위가 아닌 mm 단위로 사용한다면 범위는 100cm ~ 200cm에서 1,000mm~ 2,000mm가 된다. 이렇게 단위를 변경하면 데이터의 분포가 훨씬 넓어지는 경우가 존재한다.
- 만약, mm 단위로 키를 입력하면, 모델은 키의 영향을 과도하게 되어 정확한 예측을 어렵게 만든다. 이런 문제를 방지하기 위해 데이터를 정규화하여 모든 입력 변수가 비슷한 범위와 분포를 가지도록 조정하는 것이다. 그래야 모델이 각 입력 변수의 중요성을 적절히 반영하게 된다.
- 이 개념을 층(layer)에 적용하는 것이다. 층이 깊어질수록 층마다 분포의 차이가 발생할 가능성이 높아지므로 학습이 잘되지 않기 때문이다.
■ 과거에는 배치 입력 데이터 사이에 정규화를 수행하는 배치 정규화(batch normalization)을 사용했으나, 트랜스포머 아키텍처에서는 특정 차원에서 정규화를 수행하는 "층 정규화(layer normalization)"를 사용한다.
■ 여기서 말하는 특정 차원은 트랜스포머에서 입/출력의 차원으로 사용되는 \( d_{models} \) 차원을 말한다.
■ 아래의 그림은 \( d_{models} \) 차원의 방향의 벡터를 나타낸 것이다.

■ 정규화를 하기 위해 데이터의 평균과 표준편차(또는 분산)를 구해서 다음과 같은 식으로 계산한다.

- \( x_i \)는 벡터, 평균 \( u_i \)와 분산 \( \sigma^2_i \)는 스칼라
- \( k \)는 벡터 \( x_i \)의 차원, 벡터 \( x_{i, \; k} \)는 \( k \) 차원을 가지는 \( i \)번째 벡터 \( x \)를 의미
- 입실론은 분모가 0이 되는 것을 방지하는 값
■ 여기에 학습 가능한 파라미터인 감마와 베타를 도입해서, 다음과 같은 정규화를 수행할 수도 있다. 감마의 초깃값은 1, 베타의 초깃값은 0이다.

- \( ln_i \)는 정규화된 벡터
참고) https://hyeon-jae.tistory.com/54
매개변수 갱신 방법(2)
1. 가중치 초깃값■ 너무 큰 가중치 (매개변수)값은 학습 과정에서 과적합을 발생시킬 수 있어서 초깃값을 최대한 작은 값에서 시작하거나 가중치 감소 기법을 통해 과적합을 억제해야 한다.■
hyeon-jae.tistory.com
■ 딥러닝에서는 데이터를 어떻게 묶는지에 따라 크게 배치 정규화와 층 정규화로 구분한다. 보통 이미지 처리에서 배치 정규화를, 자연어 처리에서 층 정규화를 사용한다.
■ 자연어 처리에서 모델에 입력으로 들어가는 미니 배치에 정규화를 수행하는 배치 정규화를 사용하지 않는 이유는, 자연어 처리에서 입력으로 들어가는 문장의 길이가 제각각이기 때문이다.
■ 미니 배치로 모델을 훈련할 경우, 입력 문장들의 길이가 다른 경우가 있기 때문에, 패딩 처리를 통해 다음 그림처럼 길이를 맞춰주게 된다.

■ 모델의 입력으로 배치 데이터가 들어갈 때, 위의 그림처럼 미니 배치 [i, the, because]에 대한 임베딩 벡터가 가장 먼저 들어가고, 그다음 [am, animal, it] 순으로 들어가게 된다.
■ 이때, 첫 번째 배치의 경우 모두 실제 데이터이므로 평균과 표준편차(또는 분산)를 계산할 수 있어 배치 정규화가 가능하다. 그러나 여섯 번째 배치의 경우 패딩 토큰이 2개라서 의미 있는 실제 데이터가 1개이다.
■ 첫 번째 배치의 경우 3개의 데이터 중 3개의 데이터가 모두 실제 데이터이므로 평균과 표준편차를 올바르게 계산할 수 있지만, 여섯 번째 배치의 경우 3개의 데이처 중 1개의 데이터만 실제 데이터이므로 평균과 표준편차를 계산하기 어렵다.
■ 즉, 첫 번째 배치는 배치 정규화의 효과가 있지만, 여섯 번째 배치는 정규화의 효과가 사실상 없다. 다시 말해, 배치 정규화를 자연어 처리에 사용할 경우 정규화 효과를 보장하기 어렵다.
■ 층 정규화는 배치 정규화와 달리, 위의 \( d_{models} \) 차원의 방향의 벡를 나타낸 그림처럼 각각의 벡터의 평균과 표준편차를 구해 정규화를 수행한다.
- 예를 들어, 토큰 임베딩 벡터의 차원이 4이고, 'i'의 토큰 임베딩 벡터가 [0.1, 0.2, 0.3, 0.4], 'the'는 [0.5, 0.6, 0.7, 0.8], 'because'는 [0.1, 0.6, 0.3, 0.8]이라고 했을 때,
- 'i', 'the', 'because' 각각의 임베딩 벡터의 평균과 표준편차를 구해 정규화를 수행한다.
■ 파이토치에서 층 정규화는 torch.nn.LayerNorm()을 이용하면 된다. LayerNorm은 배치에 있는 각 항목의 평균과 분산을 계산하고, 이를 통해 정규화를 수행한다.
■ 예를 들어 [N, C, H, W] 모양의 샘플이 있을 때, LayerNorm은 각 배치에서 [C, H, W] 모양의 모든 요소에 대한 평균과 분산을 계산한다.

2.4.1 층 정규화 적용 순서
■ 트랜스포머 아키텍처에 층 정규화를 적용하는 순서에는 크게 두 가지 방식이 있다.
■ 하나는 원 논문처럼 어텐션 계층과 피드 포워드 계층 이후에 층 정규화를 적용하는 방식이다. 이 방식을 사후 정규화(post-norm)이라고 부른다.
■ 다른 하나는 "On Layer Normalization in the Transformer Architecture"라는 논문에서 제안한 방식이 있다. 여기서는 먼저 층 정규화를 적용하고 어텐션, 피드 포워드 계층을 통과했을 때 학습이 더 안정적이라는 사실을 확인했다. 이를 사전 정규화(pre-norm)이라고 부른다.
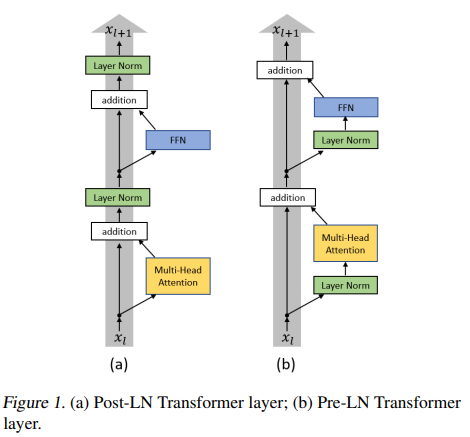
- 현재는 주로 사전 정규화가 활용된다.
'자연어처리' 카테고리의 다른 글
| 트랜스포머(Transformer) (3) (0) | 2025.04.21 |
|---|---|
| 트랜스포머(Transformer) (1) (0) | 2025.04.15 |
| 어텐션(Attention) (4) (0) | 2025.04.14 |
| 어텐션(Attention) (3) (0) | 2025.04.13 |
| 어텐션(Attention) (2) (0) | 2025.04.07 |


