어텐션(Attention) (2)

1. Seq2Seq + Attention

■ 어텐션(Attention) (1) 에서 Seq2Seq 모델에 어텐션 메커니즘을 적용할 때, Query는 Decoder의 은닉 상태, Key와 Value는 Encoder의 은닉 상태들로 설정한다고 하였다. 

■ 이렇게 설정하는 이유는 어텐션의 핵심 아이디어와 동작 방식에 기반한 것이다.

---

 

1.1 Seq2Seq + Attention의 아이디어

■ SeqSeq + Attention의 핵심 아이디어는 Decoder가 출력 단어를 예측할 때, Encoder 입력 시퀀스의 어떤 부분에 더 주목(Attention)해야 할지를 결정하는 것이다. 

■ 이를 쿼리(Query), 키(Key), 값(Value) 관점에서 설명하면 다음과 같다.

① 쿼리(Query): 디코더의 은닉 상태(Hidden State)

- 어텐션 메커니즘에서 쿼리는 현재 어떤 정보에 집중해야 하는가?를 묻는 어텐션의 주체이자, 검색 결과를 얻기 위한 검색어라고 할 수 있다.

- 디코더가 각 시점(time step)마다 다음 단어를 예측하는 구조라고 했을 때, 디코더의 현재 시점의 은닉 상태는 이전 시점에 생성된 단어들의 정보(이전 시점 디코더의 은닉 상태)와 현재 예측해야 할 단어에 대한 문맥(context) 정보(Encoder에서 전달한 은닉 상태)를 압축하여 가지고 있다고 볼 수 있다.

- 기존 Seq2Seq 모델의 문제점 중 하나는 Encoder에서 전달하는 고정 길이의 은닉 상태 벡터에 있었다. 각 입력 시퀀스에 대한 정보를 고정 길이로 압축한 context vector를 디코더에 전달하기 때문에 입력 시퀀스의 길이가 길어진다면 중요한 정보가 누락될 가능성이 크다는 것이었다. 

- 그러므로 고정 길이의 context vector를 전달 받지 않고, 디코더의 은닉 상태가 다음 단어에 대한  예측을 잘하기 위해서  "인코더가 처리한 입력 시퀀스 중 현재 어떤 정보가 필요한지"  입력 시퀀스 길이에 비례한 정보가 인코딩된 인코더의 각 시점별 은닉 상태들을 대상으로 검색하는 쿼리 역할을 한다면, 어떤 부분이 현재 예측에 가장 관련성이 높은지 파악할 수 있다.

② 키(Key): 인코더의 각 시점(time step)별 은닉 상태들(Hidden state's')

- 키는 쿼리에 대한 유사도를 계산할 대상이다. 

- 인코더는 입력 시퀀스의 각 단어(또는 토큰)를 순차적으로 처리하며 각 시점에서의 정보를 은닉 상태로 압축한다. 각 시점에서의 은닉 상태들을 $h_i, \; i = 1, 2, \cdots, T$이라고 하자.

- 이 인코더의 은닉 상태들 $h_i$는 각 시점별로 계산된 것이므로, 입력 시퀀스의 각 부분에 대한 정보를 담고 있다.

- 그러므로, 인코더의 은닉 상태들 $h_i$를 키(Key)로 사용한다면, 쿼리(Query)인 디코더의 은닉 상태와 유사도 계산을 통해 비교해서 현재 디코더 상태(Query)와 가장 관련성이 높은 입력 시퀀스 부분(Key)이 무엇인지 찾아낼 수 있다.

- 즉, 키(Key)를 인코더의 각 시점별 은닉 상태들로 사용하는 것은 인코더의 각 시점별 은닉 상태들을 일종의 '정보 식별자'로 사용하기 위해서이다.

③ 값(Value): 인코더의 각 시점(time step)별 은닉 상태들(Hidden state's')

- 키(Key)에서 인코더의 각 시점별 은닉 상태들이 일종의 '정보 식별자'의 용도로 사용되었다면, 값(Value)에서 인코더의 각 시점별 은닉 상태들은 어텐션 값을 계산하기 위한 각 시점의 '실제 정보'로 사용된다.

- 어텐션 메커니즘에서 값(Value)는 키(Key)와 쿼리(Query)의 유사도(어텐션 스코어)에 따라 가중치가 부여되어 최종적으로 전달될 정보의 내용이다. Seq2Seq 구조에 적용한다면, 최종적으로 디코더에 전달될 정보의 내용이라고 할 수 있다.    

- 실제로 디코더에게 전달하고 싶은 정보는 인코더가 입력 시퀀스를 처리하면서 생성한 각 시점의 정보, 즉 인코더 은닉 상태들이다.

- 쿼리와 키의 유사도 계산을 통해 얻어진 어텐션 스코어는 각 인코더 은닉 상태에 대한 중요도를 나타내지만, 이 어텐션 스코어는 값이 매우 다양하게 나올 수 있기 때문에 소프트맥스 함수로 정규화를 시킨다. 

- 여기서 얻이진 값은 0.0 ~ 1.0 사이의 값을 가지며 총합이 1인 어텐션 가중치(또는 어텐션 분포)이며, 특정 인코더 은닉 상태가 중요하다면, 그 값은 다른 인코더 은닉 상태에 비해 큰 값을 가지게 된다. 

- 즉, 어텐션 가중치는 각 입력 시퀀스가 얼마나 중요한지를 나타내는 가중치라고 할 수 있다.

- 이 어텐션 가중치(각 인코더 은닉 상태에 대한 중요도)를 각 인코더 은닉 상태(Value)에 곱한 후 모두 더한다. 

- 예를 들어 인코더의 은닉 상태 $h_1, h_2, h_3, h_4$가 있고, 어텐션 가중치 $a_1, a_2, a_3, a_4$가 있다고 했을 때, 각 시점의 입력 시퀀스가 얼마나 중요한지를 나타내기 위해 각 $h$에 대응되는 가중치 $a$를 적용한다. $a_1 \times h_1, a_2 \times h_2, a_3 \times h_3, a_4 \times h_4$

- 이 가중합을 통해 계산된 어텐션 값은 context vector로서, 현재 시점의 디코더 은닉 상태에게 가장 중요하다고 판돤되는 입력 시퀀스 정보들을 종합한 결과라고 할 수 있다. 

- 만약 $h_2$가 중요한 단어라서 $a_2$의 값이 0.8이라면, 나머지 $a_1, a_3, a_4$의 총합은 0.2이므로 가중합 $a_1 \times h_1 + a_2 \times h_2 + a_3 \times h_3 + a_4 \times h_4$ 결과인 context vector에는 $h_2$의 성분이 많이 포함되어 있게 된다.

- 즉, Decoder에 입력된 단어와 대응 관계인 단어의 벡터를 선택하는 작업을 가중합 연산이 담당하고 있는 것이다.

■ 위와 같은 어텐션 과정을 순서대로 나타내면 다음과 같다.

[출처] Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention) – Jay Alammar – Visualizing machine learning one concept at a time.

■ 이러한 어텐션 메커니즘 덕분에 Seq2Seq 모델은 긴 입력 시퀀스가 주어져도, 디코더가 자신의 Query와 인코더의 Key를 비교해 관련성(=attention score, attention weight)을 계산하고, 이 관련성에 따라 인코더의 Value들을 조합하여(가중합하여), 현재 예측에 가장 필요한 컨텍스트 벡터(=attention value)를 만들어 사용함으로써 모델 성능을 향상시킬 수 있다.

---

---

2. 바다나우 어텐션(Bahdanau Attention)

■ 어텐션(Attention) (1) 에서 어텐션 메커니즘을 Attention() 함수로 정의한다면, "Attention(Q, K, V) = Attention Value"로 표현할 수 있다고 하였다. 

■ 여기서 Q(Query)를 디코더의 $t - 1$ 시점의 은닉 상태를, K(Key)와 V(Value)를 인코더의 모든 시점의 은닉 상태들로 이용하는 방법이 바다나우 어텐션이다. 즉, 인코더 모든 시점의 은닉 상태를 참조하는 방법이다. 

- $t$는 어텐션 메커니즘이 수행되는 디코더의 현재 시점을 $t$라고 하자.

■ 바다나우의 구조는 다음 그림과 같다. 인코더를 통해 각 시점별 입력 시퀀스의 은닉 상태를 얻는 과정은 기존 Seq2Seq와 동일하다. Seq2Seq와 차별화되는 부분은 디코더의 은닉 상태를 계산하는 과정이다.

Bahdanau architecture [출처] Neural Machine Translation by Jointly Learning to Align and Translate

---

2.1 어텐션 스코어(Attention Score) 계산

■ 예를 들어 다음과 같은 Seq2Seq 모델에 바나다우 어텐션을 적용한다고 가정해 보자. 

[출처] https://wikidocs.net/73161

■ 인코더의 은닉 상태를 각각 $h_i, \; i = 1, 2, 3, 4$라 하고 현재 시점 $t$에서 디코더의 은닉 상태를 $s_t$라고 하자.

- 이 예시에서는 인코더의 은닉 상태와 디코더의 은닉 상태 차원이 4로 동일하다고 가정한다. 

■ 어텐션 스코어를 함수로 생각한다면, 어텐션 스코어의 입력은 Query와 Key이며, 이때 Query는 현재 시점 $t$에서 디코더의 은닉 상태이며, Key는 인코더의 은닉 상태들이다. 

■ 바다나우 어텐션은 $t - 1$ 시점에서의 디코더 은닉 상태를 Query로 사용하며 인코더의 모든 시점의 은닉 상태를 Key와 Value로 사용한다.

■ 즉, 바다나우 어텐션에서 어텐션 스코어 함수는 $s_{t-1}$과 $h_i$를 입력으로 사용하며, 어텐션 스코어 계산 방법은 다음과 같다.

$\text{Attention Score}(s_{t-1}, \; h_i) = W^T_a \text{tanh} \left( W_b \cdot s_{t-1} + W_c \cdot h_i \right)$

- $W_a, W_b, W_c$는 학습 가능한 파라미터인 가중치 행렬이다.

■ 이 예에서는 인코더의 은닉 상태가 4개이다. 그러므로 $s_{t-1}$과 $h_1, h_2, h_3, h_4$의 어텐션 스코어를 각각 계산해야 한다. 

■ 이때, 병렬 연산을 위해 인코더의 은닉 상태 벡터 $h_1, h_2, h_3, h_4$를 아래 그림처럼 하나의 행렬 $H$로 합칠 수 있으며, 어텐션 스코어 함수의 식은 다음과 같이 나타낼 수 있다.

 

$\text{Attention Score}(s_{t-1}, \; H) = W^T_a \text{tanh} \left( W_b \cdot s_{t-1} + W_c \cdot H \right)$

■ 먼저, $W_b \cdot s_{t-1}$과 $W_c \cdot H$의 계산이 각각 다음과 같다고 하자.

[출처] https://wikidocs.net/73161

■ \( W_b \cdot s_{t-1} \)과 $W_c \cdot H$을 더한 후, 하이퍼볼릭탄젠트 함수의 입력으로 넣은 $\text{tanh} \left( W_b \cdot s_{t-1} + W_c \cdot H \right)$ 계산 결과가 다음과 같다고 하자. 

- 여기서 덧셈은 columnwise sum을 의미한다.

[출처] https://wikidocs.net/73161

■ 이제 $W^T_a$와 $\text{tanh} \left( W_b \cdot s_{t-1} + W_c \cdot H \right)$를 곱하여, Query인 $t - 1$ 시점에서의 디코더 은닉 상태와 Key인 인코더의 모든 시점의 은닉 상태 $h_1, h_2, h_3, h_4$의 유사도가 기록된 어텐션 스코어 벡터 $e^t$를 얻을 수 있다.

[출처] https://wikidocs.net/73161

$e^t = W^T_a \text{tanh} \left( W_b \cdot s_{t-1} + W_c \cdot H \right)$

---

2.2 어텐션 분포(Attention Distribution) 계산 

■ 어텐션 분포(어텐션 가중치)를 얻기 위해 다음과 같이 어텐션 스코어 벡터에 소프트맥스 함수를 적용하면 된다. 

[출처] https://wikidocs.net/73161

■ 소프트맥스 함수의 결과인 어텐션 분포의 각 원소는 0.0 ~ 1.0 사이의 스칼라이며, 모든 원소의 총합은 1이 되는 확률 분포가 된다. 이를 어텐션 분포(Attention Distribution)라고 하며, 각 원소의 값을 어텐션 가중치(Attention Weight)라고 한다.

---

2.3 어텐션 값(Attention Value) 계산

■ 어텐션의 최종 결과값인 어텐션 값을 얻기 위해서 Value인 모든 시점의 인코더의 은닉 상태와 어텐션 가중치들을 다음과 같이 가중합(weighted sum)하면 된다. 

[출처] https://wikidocs.net/73161

■ 가중합된 벡터는 인코더의 문맥을 포함하고 있다고 하여, 컨텍스트 벡터(context vector)라고 부른다.

■ 이 예에서 어텐션 가중치를 각각 $a_1, a_2, a_3, a_4$라고 했을 때, $a_1 = 0.1, a_2 = 0.6, a_3 = 0.2, a_4 = 0.1$이라면, 가중합 $a_1 \times h_1, a_2 \times h_2, a_3 \times h_3, a_4 \times h_4$ 결과인 context vector에는 $h_2$의 성분이 많이 포함되어 있게 된다. 

■ 여기까지의 과정을 어텐션 메커니즘으로 나타낸다면, 바다나우 어텐션의 메커니즘은 다음과 같다.

■ $s_t$가 현재 시점의 디코더 은닉 상태라고 했을 때, 바다나우 어텐션은 $s_{t-1}$과 모든 시점의 인코더 은닉 상태를 묶은 행렬 $H$를 Query와 Key로 입력받아 유사도(어텐션 스코어)를 계산한다. 

■ 이때, 가중치 행렬 $W_b$와 $W_c$를 각각 곱한 $W_b \cdot s_{t-1}$과 $W_c \cdot H$를 더하는데 여기서 +는 columnwise sum 연산이다. 

- 바다나우 어텐션은 이렇게 인코더의 은닉 상태와 디코더의 은닉 상태의 선형 결합을 수행하기 때문에 Additive Attention이라고도 불린다.

■  $W_b$의 크기가 $n \times n$, $s_{t-1}$의 크기가 $n \times 1$, $W_c$의 크기가 $n \times n$, $H$의 크기가 $n \times T$라고 했을 때,

■ $n \times 1$ 크기의 $W_b \cdot s_{t-1}$과 $n \times T$ 크기의 $W_c \cdot H$에 대해 columnwise sum 연산을 수행하여 $n \times T$ 크기의 벡터 또는 행렬을 얻는다.

■ 여기에 tanh 함수를 통과 시킨 다음 $1 \times n$ 크기의 $W^T_a$를 곱해 $1 \times n \times n \times T  = 1 \times T$ 크기의 어텐션 스코어 벡터를 얻는다.

■ 그다음, $1 \times T$ 크기의 어텐션 스코어를 소프트맥스 함수에 통과시켜 $1 \times T$ 크기의 어텐션 분포 $a_t$를 얻는다. 

■ 최종적으로 Value인 $H$에 $a^T_t$를 곱하여 $n \times T \times T \times 1 = n \times 1$ 크기의 어텐션 값(Attention Value)를 산출한다.

---

2.4 바다나우 어텐션

■ 바다나우 어텐션에서는 2.3에서 얻은 컨텍스트 벡터로부터 현재 시점 $t$의 디코더 은닉 상태 $s_t$를 계산한다. 

■ $t$ 시점의 LSTM 셀은 $s_t$를 계산하기 위해 이전 시점의 LSTM 셀로부터 전달받은 은닉 상태 $s_{t-1}$과 현재 시점의 입력 $x_t$를 입력으로 받는다. 여기서 $x_t$가 임베딩 계층을 통과한 임베딩된 단어 벡터라고 하자.

[출처] https://wikidocs.net/73161

■ 바다나우 어텐션에서는 2.3에서 최종적으로 얻은 컨텍스트 벡터와 현재 시점의 임베딩 벡터 $x_t$를 연결(concatenate)한 것을 다음과 같이 현재 시점의 새로운 입력으로 사용한다.

[출처] https://wikidocs.net/73161

■ 이렇게 해서 얻은 $s_t$에 출력층으로의 가중치 행렬을 곱하고 편향을 더한 뒤, 그 결과에 소프트맥스 함수를 적용하여 현재 시점의 예측값인 예측 벡터 $\hat{y}_t$를 계산한다. $\hat{y}_t = \text{Softmax} (W_y \cdot s_t + b_y)$

■ 바다나우 어텐션은 정리하면, 

- 디코더의 현재 $t$ 시점(times step)의 예측을 위해, 이전 시점의 은닉 상태 $s_{t-1}$을 Query로 사용한다. 

- 이 쿼리와 인코더의 모든 시점에서의 은닉 상태들 $H = \left\{ h_1, h_2, \cdots, h_T \right\}$를 Key로 사용하여, Query와 각각의 유사도를 계산하는 것부터 시작한다.

- 어텐션 스코어는 인코더의 은닉 상태들이 각각 디코더의 특정 시점의 은닉 상태와 얼마나 유사한지를 판단하는 수치값이다.

- 즉, $s_{t-1}$과 인코더의 각 시점의 정보 $h_i, \; i = 1, 2, \cdots, T$와 얼마나 관련이 있는지를 측정한다.

- 여기서 얻은 어텐션 스코어에 소프트맥스 함수를 적용하여 어텐션 분포(어텐션 가중치)를 얻는다. 여기서 어텐션 분포는 각 인코더의 은닉 상태 $h_i$가 현재 예측 $t$ 시점에 얼마나 중요한지를 나타내는 확률 분포이며, 모든 가중치의 합은 1이 된다.

- 인코더의 모든 시점의 은닉 상태 $H$에 해당 어텐션 가중치를 적용한 가중합을 계산하여 컨텍스트 벡터를 생성한다.

- 이 컨텍스트 벡터는 현재 $t$ 시점의 예측에 가장 중요하다고 판단되는 입력 시퀀스의 정보들을 가중합하여 종합한 결과이다.

- 생성된 컨텍스트 벡터 $c_t$는 디코더의 현재 시점의 은닉 상태 $s_t$ 계산에 사용된다.

- 즉, 컨텍스트 벡터와 이전 시점의 은닉 상태 $s_{t-1}$ 그리고 현재 시점의 입력 $x_t$를 함께 사용하여 현재 $t$ 시점의 예측을 수행한다.

■ 그러므로 이 방법은, 디코더가 $t$ 시점의 예측을 할 때 사용하는 이전 시점의 은닉 상태 $s_{t-1}$과 유사하다고 판단되는 인코더의 은닉 상태 $h_i$일수록, 해당 시점의 예측에 도움이 되는 입력값이라고 가정한 것으로 볼 수 있다. 

---

---

 

3. 닷-프로덕트 어텐션(Dot-Product Attention)

■ 닷-프로덕트 어텐션은 바다나우 어텐션의 연구를 이어받은 루옹 어텐션(Luong Attention) 중 하나이다.

■ 바다나우 어텐션과의 차이점은, 바다나우 어텐션은 Query로 디코더의 $t - 1$ 시점의 은닉 상태를 사용한 것과는 달리 루옹 어텐션에서는 $t$ 시점의 은닉 상태를 사용한다.

■ 즉, 닷-프로덕트 어텐션에서 Query로 디코더의 $t$ 시점의 은닉 상태를 이용한다.

■ 또한, K(Key)와 V(Value)로 인코더의 모든 시점 혹은 일부 시점의 은닉 상태들을 이용한다. 

- 글로벌 어텐션(Global Attention)은 바다나우 어텐션처럼 인코더의 모든 시점의 은닉 상태를 참조하는 방법이다.

- 그래서 바다나우 어텐션과 비교했을 때, 차이점은 Query와 Key의 관계를 계산하는 방법. 즉, 어텐션 스코어 함수에만 차이가 있다. 어텐션 스코어를 계산하는 방법으로는 다음과 같이 dot, general, concat 방법이 있다. 

$\text{ Attention Score }(s_t, H) = \begin{cases} s_t^T H, & \text{dot} \\ s_t^T W_a H, & \text{general} \\ W_a^T \tanh(W_b [s_t ; H]), & \text{concat} \end{cases}$

-- 여기서 $W$는 학습 가능한 가중치 행렬이다.

- 글로벌 어텐션은 바다나우 어텐션처럼 모든 시점의 은닉 상태를 참조하므로, 인코더의 마지막 시점이 $T$라고 했을 때,   $H = \left\{ h_1, h_2, \cdots, h_T \right\}$이다. 즉, 모든 시점 $1, \cdots, T$의 은닉 상태를 참조한다.

- 위의 글로벌 어텐션 중 이름이 dot이라고 붙여진 어텐션 스코어 함수가 닷-프로덕트 어텐션이다. 여기서 dot 함수가 가장 간단한 방법이다. 유사도를 구하는 가장 간단한 방법은 내적을 계산하는 것이기 때문이다.

- Global Attention 외에도 인코더의 은닉 상태의 일부만 참조하는 Local Attention이 있다. 이렇게 Seq2Seq + Attention 모델에 쓰일 수 있는 다양한 어텐션 종류가 있으며, 차이점은 어텐션 스코어를 계산하는 방법이다.  

---

3.1 어텐션 스코어(Attention Score) 계산

■ 마찬가지로, 인코더의 은닉 상태를 각각 $h_i, \; i = 1, 2, 3, 4$라 하고 현재 시점 $t$에서 디코더의 은닉 상태를 $s_t$라고 하자.

- 이 예시에서는 인코더의 은닉 상태와 디코더의 은닉 상태 차원이 4로 동일하다고 가정한다. 

[출처] https://wikidocs.net/73161

■ 닷-프로덕트 어텐션에서는 어텐션 스코어를 계산하기 위해 다음과 같이 $s_t$와 각 시점의 은닉 상태의 내적을 계산한다.

[출처] https://wikidocs.net/73161

- $\vec{a} = (a_1, a_2, \dots, a_n), \quad \vec{b} = (b_1, b_2, \dots, b_n)$이라면, $\vec{a}, \vec{b}$의 내적 $\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \dots + a_n b_n = \vec{b}^T \vec{a}$

- 내적은 두 벡터가 얼마나 유사한 방향을 가지고 있는지 나타내는 척도로 사용할 수 있다. 그 이유는 두 벡터가 비슷한 방향을 가질수록 내적 값은 커지고, 서로 다른 방향을 가질수록 내적 값이 작아지기 때문이다.

- 이는 내적을 다음과 같이 두 벡터의 크기와 코사인 값의 곱으로 나타낼 수 있기 때문이다.

- 여기서 $\theta$는 두 벡터 사잇각이며, $0 \leq \theta \leq \pi$이다.

- 두 벡터의 방향이 완전히 같다면 \( \theta = 0 ˚ \)가 되어 $\cos \theta = 1$이 되므로, $\| a \| \| b \|$의 값이 내적 결과가 된다.

- 두 벡터가 서로 직교한다면 \( \theta = 90 ˚ \)가 되어 $\cos \theta = 0$, 그러므로 내적 값은 0

- 두 벡터가 서로 반대 방향이라면 \( \theta = 180 ˚ \)가 되어 $\cos \theta = -1$이 된다. 그러므로  $- \| a \| \| b \|$의 값이 내적 결과가 된다.

- 이때, $\| a \| \| b \|$는 두 벡터의 크기이다. 그러므로 두 벡터가 비슷한 방향을 가질수록 내적 값이 커지는 것이다. 

■ $H = \left\{ h_1, h_2, \cdots, h_T \right\}$라고 했을 때, 닷-프로덕트 어텐션은 인코더의 모든 시점의 은닉 상태를 참조하므로 닷-프로덕트 어텐션의 어텐션 스코어 함수는 다음과 같이 표현할 수 있다.

$\text{Attention Score}(s_t, \; H) = s^T_t  H = [s^T_t \cdot h_1, s^T_t \cdot h_2, \cdots, s^T_t \cdot h_T ]$

---

3.2 어텐션 분포(Attention Distribution) 계산 

■ 어텐션 분포(어텐션 가중치)를 계산하는 방법은 2.2와 동일하다. 3.1에서 얻은 어텐션 스코어에 소프트맥스 함수를 적용하면 된다. 

---

3.3 어텐션 값(Attention Value) 계산

■ 어텐션 값을 계산하는 방법도 2.3과 동일하다. 3.2에서 얻은 어텐션 분포(어텐션 가중치)와 Value인 모든 시점의 은닉 상태들의 가중합을 계산하면 된다. 

■ 마찬가지로, 여기서 얻은 어텐션 값은 인코더의 문맥을 포함하고 있으므로 컨텍스트 벡터라고 할 수 있다. 

■ 여기까지의 과정을 어텐션 메커니즘으로 나타낸다면, 닷-프로덕트 어텐션의 메커니즘은 다음과 같다.

---

3.4 닷-프로덕트 어텐션

■ 어텐션 메커니즘은 어텐션 값(컨텍스트 벡터)을 디코더의 은닉 상태를 연결(concatenate)하여 하나의 벡터로 결합하는 과정을 거친다.

■ 바다나우 어텐션에서는 어텐션 값과 입력 값을 연결했다면, 닷-프로덕트 어텐션에서는 어텐션 값을 $s_t$에 연결한다.

■ 디코더 $t$ 시점의 어텐션 값을 $a_t$라고 한다면, $a_t$를 디코더의 $t$ 시점 은닉 상태 $s_t$와 다음과 같이 연결한다.

[출처] https://wikidocs.net/73161

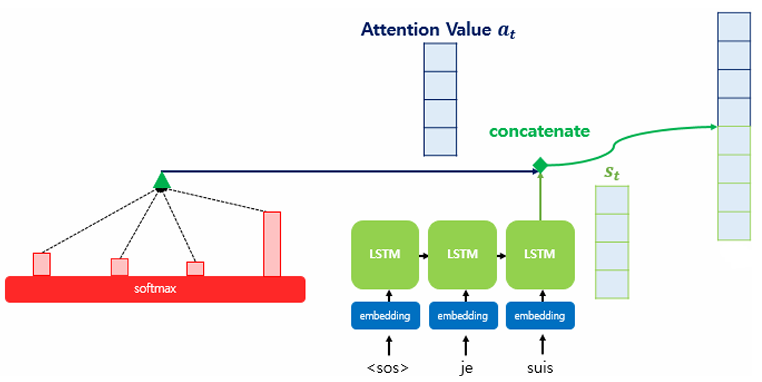
■ 이를 수식으로 표현하면 다음과 같다.

$\tilde{s}_t = \tanh(\mathbf{W}_c [a_t ; s_t] + \mathbf{b}_c)$

■ 여기서 계산된 $\tilde{s}_t$는 출력층의 입력으로 들어가서 $t$ 시점의 예측 결과인 $\hat{y}_t$를 계산한다. 

$\hat{y}_t = \text{Softmax}(W_y \tilde{s}_t + b_y)$

■ 바다나우 어텐션과 비교했을 때, 닷-프로덕트 어텐션은 크게 세 가지 차이점이 있다.

■ 첫 번째는 Query에 $t - 1$ 시점 대신 $t$ 시점의 디코더 은닉 상태를 이용한다는 점, 두 번째는 Query와 Key의 관계를 계산하는 방식, 세 번재는 어텐션 값을 디코더에서 연결하는 방식이다. 

---