1. 기존 Seq2Seq 모델의 한계
■ 기존의 Seq2Seq 모델은 Encoder-Decoder 구조로 구성되어져 있었다. 여기서 Encoder는 입력 시퀀스를 하나의 고정 길이 벡터(context vector)로 압축하였고, Decoder는 이 벡터를 받아 출력 시퀀스를 생성했다.
■ 하지만, 이러한 구조는 Encoder에서 입력 시퀀스를 고정 길이 벡터로 압축하기 때문에, 입력 시퀀스의 길이가 길어지면, 입력 시퀀스의 정보가 일부 손실된다는 단점이 있었다.
■ 이 단점을 보완하기 위해 어텐션(Attention)을 RNN 계층의 보정을 위한 용도로 사용하였다.
■ 어텐션을 사용해도 단점이 남아 있는데, 그것은 바로 RNN은 "병렬 처리가 불가능"하다는 것이다.
■ Encoder와 Decoder에 RNN을 사용하면, RNN은 시간축 방향을 따라 순차적으로 계산하기 때문에 병렬 계산이 불가능하다.
■ RNN은 다음 그림과 같이 텍스트를 순차적으로 하나씩 입력하는 형태이다.

■ \( x \)가 입력 토큰이라고 했을 때, \( h \)는 입력 토큰을 RNN 모델에 입력했을 때의 출력값이다. 위의 그림처럼 이전 토큰의 출력을 다시 동일한 모델에 입력으로 사용하기 때문에 입력을 병렬적으로 처리하지 못하는 구조이다.
■ 이렇게 순차적으로 처리하기 때문에 학습 속도가 느리고, 입력이 길어지면 먼저 입력한 토큰의 정보가 희석되면서 성능이 떨어진다는 문제가 있었다.
■ 또한, 성능을 높이기 위해 출력 방향으로 층을 깊게 쌓으면, 기울기 소실(gradient vanishing)이나 기울기 폭주(gradient exploding)이 발생하며 학습이 불안정했다.
■ 이렇게 하나씩 순차적으로 처리하는 RNN을 사용하지 않고, 어텐션만으로 Encoder와 Decoder를 만들어서 병렬 계산을 할 수 있도록 셀프 어텐션(self-attention)이라는 개념을 도입한 것이 바로 "Attention Is All You Need"라는 논문에서 제안한 트랜스포머(Transformer) 아키텍처이다.
- 셀프 어텐션은 입력 문장 내의 각 단어가 서로 어떤 관련이 있는지 계산해서 각 단어의 표현(representation)을 조정하는 역할을 한다.
[1706.03762] Attention Is All You Need
Attention Is All You Need
The dominant sequence transduction models are based on complex recurrent or convolutional neural networks in an encoder-decoder configuration. The best performing models also connect the encoder and decoder through an attention mechanism. We propose a new
arxiv.org
2. 트랜스포머 아키텍처
■ 트랜스포머 아키텍처는 다음 그림과 같다.

■ 트랜스포머도 "언어를 이해하는 Encoder"와 "언어를 생성하는 Decoder" 부분으로 나뉘는 것을 볼 수 있다.
■ 단, RNN을 사용하는 기존 Seq2Seq 구조에서는 Encoder와 Decoder에서 각각 RNN이 \( t \)개의 시점(time step)을 가지는 구조였다면, 트랜스포머는 Encoder와 Decoder가 각각 하나의 단위로 N개씩 구성되는 구조인 것을 볼 수 있다.
■ 즉, Encoder라는 블록과 Decoder라는 블록을 반복 사용하는 구조라고 할 수 있다. 동일한 블록을 반복해서 사용하기 때문에 확장이 용이하다. 즉, 더 깊은 모델을 만들어도 학습이 잘된다. 또한 병렬 연산이 가능하므로 학습 시간이 단축되며, 입력이 길어져도 성능이 거의 떨어지지 않는다.
- 트랜스포머를 제안한 논문에서는 Encoder와 Decoder의 개수를 각각 6개씩 사용하였다.
■ 또한, 기존 임베딩 방법과 달리 입력을 임베딩(Embedding)층을 통해 변환된 임베딩에 "위치 인코딩(Positional Encoding)"을 거쳐 문장의 위치 정보를 더한 것을 입력 임베딩으로 사용한다.
■ 그리고 Encoder와 Decoder 모두 어텐션으로 구성되어져 있는 것을 볼 수 있는데,
■ Encoder에서 "층 정규화(layer normalization)", "멀티 헤드 어텐션(multi-head attention)", 피드 포워드(feed forward)" 층을 거쳐 문장을 이해하고, 그 결과를 Decoder에 전달한다.
■ Decoder에서도 Encoder와 유사하게 층 정규화, 멀티 헤드 어텐션 연산을 수행하면서 크로스 어텐션 연산을 통해 Encoder가 전달한 데이터를 출력과 함께 종합해서 피드 포워드 층을 거쳐 결과를 생성한다.
2.1 위치 인코딩(Positional Encoding)
■ 트랜스포머에서 텍스트를 모델에 입력하기 위한 임베딩으로 변하는 과정은 크게 세 가지로, 다음과 같이 표현할 수 있다.

■ 먼저, 텍스트를 적절한 단위로 나눠 각 토큰에 정수 아이디(또는 인덱스)를 부여하는 토큰화(tokenization)을 수행한다. 그다음, 임베딩 계층을 통해 토큰의 정수 인덱스를 임베딩으로 변환한다. 마지막으로 위치 인코딩 계층을 통해 위치 정보를 담고 있는 위치 임베딩을 추가하여 최종적으로 모델에 입력할 임베딩을 만든다.
2.1.1 토큰화
■ 토큰화는 텍스트를 적절한 단위로 나누고 각 토큰에 정수 인덱스를 부여하는 것을 말한다.
■ 영어는 크게 띄어쓰기 단위(단어 단위), 작게는 알파벳(또는 문자) 단위로 나눌 수 있었고, 한글은 크게는 단어 단위, 작게는 자모(자음과 모음) 단위로 나눌 수 있었다. 음절은 중간 정도 단위로 볼 수 있다.
■ 각 토큰에 정수 인덱스를 부여했다면, 어떤 토큰이 어떤 정수 인덱스(또는 아이디)로 연결됐는지 기록한 단어 집합(vocabulary)를 만들어야 했다.
■ 이때, 단어 단위처럼 큰 단위를 기준으로 토큰화를 한다면 텍스트의 의미가 잘 유지된다는 장점이 있었지만, 단어 집합이 텍스트에 등장하는 단어 수만큼의 크기를 갖게 된다. 또한, 단어 집합에 등록되지 않은 새로운 단어를 처리하지 못하는 OOV(Out Of Vocabulary, 단어 집합에 없는 단어) 문제가 발생한다는 단점이 있었다.
■ 반대로 작은 단위로 토큰화하는 경우, 사전의 크기가 작아지고 OOV 문제도 줄일 수 있다는 장점이 있었지만 텍스트의 의미가 유지되지 않는다는 단점이 있었다.
■ 예를 들어, "hello ~~ "라는 문장을 단어 단위로 토큰화했을 때, 'hello'라는 단어 형태가 유지되므로 텍스트의 의미가 잘 유지될 수 있다. 다만, 단어 집합 내에 없는 새로운 단어는 처리할 수 없다.
■ 해당 문장을 작은 단위로 토큰화한다면, 'h', 'e', 'l', 'o'가 단어 집합에 등록된다.OOV 문제를 줄일 수 있지만, 텍스트의 의미를 유지시키는 것이 어렵다는 것을 직관적으로 알 수 있다.
- 한글도 마찬가지이다. "도시 ~~"라는 문장을 단어 단위로 토큰화하면 "도시", 자모 단위로 토큰화하면 'ㄷ', 'ㅗ', 'ㅅ', 'ㅣ' 가 되기 된다.
■ 이렇게 작은 단위와 큰 단위로의 토큰화는 모두 각각의 장단점이 뚜렷하다.
■ 그래서 최근에는 자주 등장하는 단어. 즉, 빈도수가 높은 단어는 단어 단위 그대로 유지하고, 빈도수가 낮은 단어는 작은 단위로 나눠 텍스트의 의미를 최대한 유지하면서, 단어 집합의 크기를 효율적으로 유지하고 OOV 문제도 줄일 수 있는 서브워드(subword) 토큰화를 사용한다.
2.1.2 임베딩으로 변환하기
■ 예를 들어, 다음과 같이 띄어쓰기 단위를 기준으로 토큰화를 수행했다고 하자.
input_text = "나는 도시 여행을 좋아한다"
input_text_list = input_text.split()
# 단어 집합 생성
stoi = {word:index for index, word in enumerate(input_text_list)}
itos = {index:word for index, word in enumerate(input_text_list)}
print('str2index', stoi)
print('index2str', itos)
```#결과#```
str2index {'나는': 0, '도시': 1, '여행을': 2, '좋아한다': 3}
index2str {0: '나는', 1: '도시', 2: '여행을', 3: '좋아한다'}
````````````
■ 딥러닝 모델이 위와 같이 단어 집합에 등록된 토큰을 처리하기 위해서는 입력으로 들어오는 토큰과 토큰 사이의 관계를 계산할 수 있어야 한다.
■ 토큰과 토큰 사이의 관계를 계산하기 위해서 토큰의 의미를 숫자로 표현할 수 있어야 한다.
■ 각 토큰에 부여한 정수 인덱스는 하나의 숫자일 뿐이므로 토큰의 의미를 담을 수 없다. 토큰의 의미를 숫자로 표현하기 위해서는 최소 2개 이상의 숫자 집합인 벡터(vector)여야 한다.
■ 이는 데이터의 의미를 담아 숫자 집합으로 변환하는 임베딩(embedding) 계층을 통해 만들 수 있다.
- 파이토치가 제공하는 nn.Embedding 클래스를 사용하면 토큰의 정수 인덱스(또는 아이디)를 룩업 테이블 연산을 통해 임베딩 벡터로 변환할 수 있다.
token_ids = [stoi[word] for word in input_text_list]
token_ids
```#결과#```
[0, 1, 2, 3]
````````````■ token_ids의 0, 1, 2, 3은 순서대로 '나는', '도시', '여행을', '좋아한다' 토큰에 대응되는 정수 인덱스이다.
import torch
import torch.nn as nn
embedding_dim = 5
embedding_layer = nn.Embedding(len(stoi), embedding_dim)
embedding_layer.weight
```#결과#```
Parameter containing:
tensor([[-0.5092, -0.4318, -0.0724, 0.1522, -0.4114],
[-0.5533, -0.4431, -0.3247, 1.1151, -0.7675],
[ 0.3095, 0.8714, -0.2308, 0.3459, 0.7342],
[ 0.0079, -0.5213, 2.0448, 1.4095, 0.3935]], requires_grad=True)
````````````■ 파이토치의 nn.Embedding 클래스로 만든 단어 집합이다. 위의 embedding_layer는 단어 집합의 크기가 4이고, 사용자가 지정한 embedding_dim=5 차원의 임베딩을 생성하는 임베딩 계층이다.
■ 즉, 4 x 5 크기의 행렬이 만들어진다. 여기서 4는 단어 집합에 등록된 단어(또는 토큰)의 개수, 5는 사용자가 지정한 임베딩 벡터의 차원이다. 각 벡터의 값은 랜덤 초기화된다.
■ 이렇게 만든 임베딩 계층에 토큰 아이디 텐서를 통과시키면, 다음과 같이 룩업 테이블 연산이 수행되어, 각 토큰은 임베딩 벡터로 변환된 상태가 된다.
embedded = embedding_layer(torch.tensor(token_ids))
embedded.shape, embedded
```#결과#```
(torch.Size([4, 5]),
tensor([[-0.5092, -0.4318, -0.0724, 0.1522, -0.4114],
[-0.5533, -0.4431, -0.3247, 1.1151, -0.7675],
[ 0.3095, 0.8714, -0.2308, 0.3459, 0.7342],
[ 0.0079, -0.5213, 2.0448, 1.4095, 0.3935]],
grad_fn=<EmbeddingBackward0>))
````````````■ 지금의 임베딩 벡터는 토큰의 의미가 담긴 벡터가 아니다. 그저 입력 토큰의 정수 인덱스(또는 아이디)를 5차원의 임의의 벡터로 변환한 상태이다.
■ 임베딩 계층이 단어의 의미를 담기 위해서는 딥러닝 모델이 학습 데이터로 훈련되어야 한다. 전체 모델이 학습되는 학습 과정(순전파&역전파)에서 위의 임베딩 계층도 학습되면서 점차 토큰의 의미를 잘 반영한 임베딩으로 업데이트된다.
2.1.3 위치 인코딩
■ RNN과 트랜스포머의 가장 큰 차이점은 입력을 순차적으로 처리하는지 여부이다.
■ RNN이 자연어 처리에 유용했던 이유는 입력 단어를 순차적으로 입력받아 처리하는 RNN의 특성때문에 자연스럽게 각 단어의 위치(또는 순서) 정보가 고려된다는 점에 있었다.
■ 트랜스포머는 순차적인 처리 방식인 RNN을 버리고, 모든 입력을 동시에 처리하기 때문에 각 단어의 순서 정보가 사라지게 된다. 하지만 텍스트에서 '순서'는 매우 중요한 정보이므로, 단어의 순서 정보를 다른 방식으로 추가할 필요가 있다.
■ 그래서 각 단어의 임베딩 벡터에 순서 정보를 더하여 모델의 입력으로 사용하는데, 순서 정보를 더하는 역할을 위치 인코딩(positional encoding)이 담당한다.

■ 임베딩 벡터가 위치 인코딩과 더해지는 과정을 시각화하면 다음 그림과 같다.

■ Attention Is All You Need 논문에서는 사인(sine)과 코사인(cosine)을 활용한 수식을 통해 위치에 대한 정보를 입력한다.
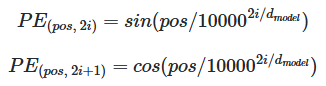
■ 트랜스포머는 위의 사인과 코사인 수식의 값을 임베딩 벡터에 더하는 방식으로 아래의 그림과 같이 단어의 위치 정보를 추가하였다. 아래의 그림은 차원이 4인 임베딩 벡터에 위치 인코딩을 더하는 과정을 나타낸다.

- \( pos \)는 입력 문장에서의 임베딩 벡터의 위치, \( i \)는 임베딩 벡터 내의 차원의 인덱스를 의미한다.
- 사인, 코사인 수식에서 \( d_{model} \)은 트랜스포머의 모든 층의 출력 차원을 의미하는 하이퍼파라미터이다.
- 즉, 각 Encoder와 Decoder가 다음 층의 Encoder와 Decoder로 값을 보낼 때에도 \( d_{model} \) 차원을 유지한다. 임베딩 벡터의 차원 또한 \( d_{model} \)이다.
■ 위의 사인, 코사인 수식에 따르면, \( i \)가 짝수인 경우에는 사인 함수의 값을, 홀수인 경우에는 코사인 함수의 값을 사용한다.
■ 즉, \( i \)에 따라 사인/코사인 값이 달라지므로 이를 통해 같은 단어라도 위치가 다르면, 다른 인코딩 값이 더해지기 때문에 최종 입력 임베딩 벡터가 달라지므로, 모델이 순서를 구분할 수 있다.
2.1.3.1 절대적 위치 인코딩(absolute position encoding)
■ 위치 인코딩은 크게 절대적 위치 인코딩과 상대적 위치 인코딩으로 분류된다.
■ 입력 시퀀스의 각 위치마다 해당 위치를 나타내는 고유한 임베딩을 토큰 임베딩에 더하는 인코딩 방식이 절대적 위치 인코딩이다. 즉, 절대적인 위치에 대한 정보를 인코딩하는 방식으로, 다음 그림처럼 시퀀스 내의 특정 위치와 연결된다.
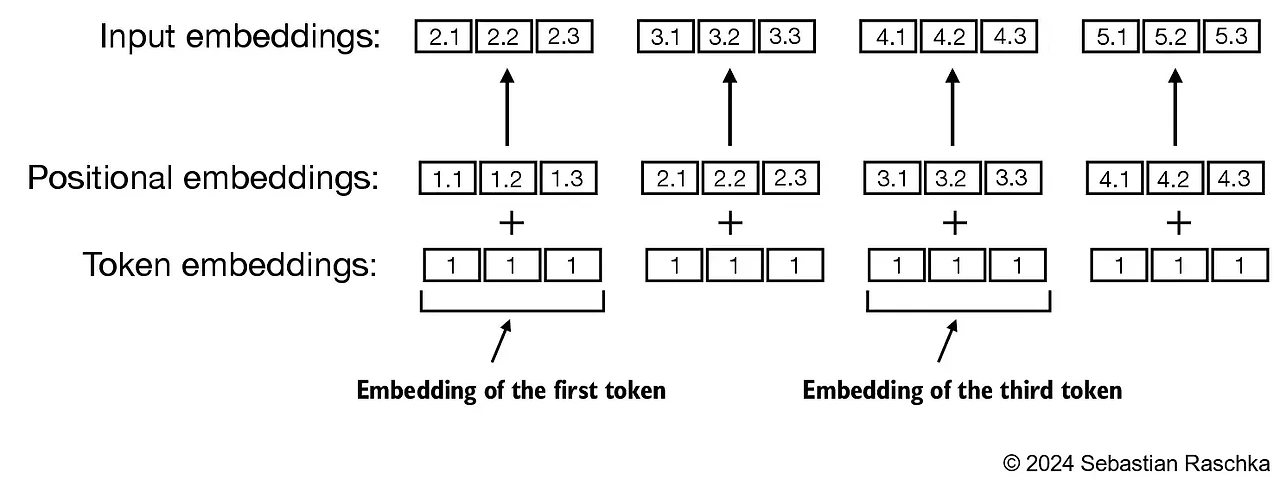
■ 입력 시퀀스의 각 위치마다 해당 위치를 나타내는 고유한 임베딩인 포지셔널 임베딩이 토큰 임베딩에 더해지는 것을 볼 수 있다.
■ 절대적 위치 인코딩도 다시 2가지 방법으로 나눌 수 있는데, ① 데이터로부터 학습하는 방법, ② 정현파 함수(Sinusoidal function)를 통해 구하는 방법이 있다. 트랜스포머 논문에서 제안된 방식이 ②이다.
■ 수식을 통해 위치 정보를 추가하는 방식이나, 위치 정보를 학습하는 방식 모두, 위의 그림처럼 입력 토큰의 위치에 따라 고정된 임베딩을 더해주기 때문에 절대적 위치 인코딩이라고 부르는 것이다.
- 두 방법이 성능은 대체적으로 유사하다.
- 정현파는 사인파(sine wave), 코사인파(cosine wave)를 총칭하는 말이다.

■ 예를 들어, 트랜스포머 논문에서 제안된 사인/코사인 수식을 사용할 경우, 각 위치마다 얻게 되는 임베딩 벡터는 고유한 벡터이다. 각각의 위치에 대해 서로 독립적인 임베딩 벡터를 얻게 된다. 또한, 간단하게 구현할 수 있다는 장점이 있다.
■ 다만, 모든 위치에 대해 동일한 방식으로 인코딩하므로, 단어 간의 상대적인 거리, 관계를 표현하기 어렵다. 다음 그림처럼 바로 옆에 위치한 토큰 pos1-pos2의 연관성이 멀리 떨어진 토큰 pos1-pos500 간의 연관성보다 중요하다는 것을 인코딩할 수 없다.

■ 즉, 절대적 위치 인코딩 방식은, 토큰과 토큰 사이의 상대적인 위치 정보를 활용하지 못한다는 단점이 있다. 즉, 토큰 간의 상대적인 거리에 따른 중요도를 반영할 수 없다는 단점이 있다.
■ 또한, 모델이 훈련 중에 학습 데이터에서 보지 못한 긴 텍스트를 추론하는 경우, 성능이 떨어진다는 문제가 있다. 트랜스포머에서 제안된 사인/코사인 수식을 사용한 절대적 위치 인코딩은 이론적으로는 무한한 길이에 대한 값을 생성할 수 있다.
■ 만약, 학습 데이터 중 최대 길이가 \( L_{max} \)라고 할 때, 추론 과정에서 \( L_{max} \)를 넘어가는 위치에 대한 인코딩 값은 모델 입장에서는 새로운 패턴이 된다.
■ 추론 과정에서 \( L_{max} \)를 넘어가는 위치에 대해서도 사인/코사인 함수 자체는 값을 제공하지만, 모델이 이 새로운 위치 값들을 어떻게 해석할지에 대한 학습이 부족하여 성능 저하로 이어질 수 있다.
■ 이러한 절대적 위치 인코딩의 한계를 개선하기 위해 제안된 방법론이 바로 상대적 위치 인코딩이다.
2.1.3.2 상대적 위치 인코딩(relative position encoding)
■ 상대적 위치 인코딩은 '각 토큰의 위치가 몇 번째인가'라는 "정확한 위치(절대적인 위치 정보)"보다는 '두 토큰 간의 거리가 얼마인가, 얼마나 떨어져 있는가'라는 "상대적인 위치 정보"를 인코딩하는 방법이다.
■ 즉, 상대적 위치 인코딩은 다음 그림과 같이 하나의 토큰이 아닌, 두 토큰 간의 상대적 거리(또는 위치)에 중점을 두고, 얼마나 떨어져 있는지에 따라 관계를 학습한다. 그러므로 모델이 훈련 중에 보지 못한 길이의 시퀀스에 대해서도 잘 일반화할 수 있다는 장점이 있다.

■ 다만, 절대적 위치 인코딩 방식보다 속도가 느리다는 단점이 있다. 절대적 위치 인코딩 방식은 단어 임베딩에 위치 임베딩을 더하는 반면, 상대적 위치 인코딩은 추론 과정에서 토큰을 생성한다고 했을 때, 위치 임베딩을 다시 구하는 작업을 반복해서 수행해야 하기 때문이다.
■ 두 가지 위치 인코딩 방식 모두 토큰 간의 순서와 관계를 이해할 수 있게 도와준다. 어떤 방식을 선택할지는 주로 응용 분야와 데이터의 특성에 따라 달라진다.
■ 이러한 상대적 위치 인코딩의 한계점을 개선한 임베딩 방법이 Rotary Positional Embedding이다.
참고) Rotary Positional Embeddings: Combining Absolute and Relative - YouTube
참고) https://hyen4110.tistory.com/154
'자연어처리' 카테고리의 다른 글
| 트랜스포머(Transformer) (3) (0) | 2025.04.21 |
|---|---|
| 트랜스포머(Transformer) (2) (0) | 2025.04.19 |
| 어텐션(Attention) (4) (0) | 2025.04.14 |
| 어텐션(Attention) (3) (0) | 2025.04.13 |
| 어텐션(Attention) (2) (0) | 2025.04.07 |


