1. 행렬식(Determinant)의 특성
1.1 행렬식의 3가지 주요 특성
■ 행렬식의 계산 결과는 숫자이고, 행렬식은 정방행렬에서만 정의된다. 즉, 행렬식은 정방행렬에서만 정의되는 숫자이다.
■ 이러한 행렬식은 주요한 3가지 특성을 갖고 있으며, 이 3가지 속성이 행렬식을 정의한다. 첫 번째는 \( \text{det} I = 1 \). 두 번째는 행을 교환하면 행렬식의 부호가 반대로 바뀐다는 것이다.
■ 1번 특성은, 예를 들어 다음과 같은 \( 2 \times 2 \) 단위행렬이 있다면, 이 단위행렬의 행렬식 값은 다음과 같이 1이 된다는 것이다.
\( \det A = |A| = \begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad - bc \)
\( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
\( \det A = \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = (1 - 0) = 1 \)
■ 2번 특성은 다음과 같이 행을 바꿀 경우 행렬식 값의 부호가 반대로 바뀌는 것을 의미한다.
\( A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \rightarrow \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
\( \det A = \begin{vmatrix} 0 & 1 \\ 1 & 0 \end{vmatrix} = (0 - 1) = -1 \)
■ 위의 예시와 같이 단위 행렬에서 임의의 행을 교환하면 치환 행렬(permutation matrix)이 되는 것을 볼 수 있다. 이를 통해 모든 치환 행렬의 행렬식은 1혹은 -1이 된다는 것을 알 수 있다. 그 이유는 행 교환의 횟수가 짝수면 +1, 홀수면 -1이 되기 때문이다.
■ 3번 특성은 다음과 같이 하나의 행에서 공통 인수를 묶어서 행렬식 밖으로 빼낼 수 있다는 것과
\( \begin{vmatrix} ta & tb \\ c & d \end{vmatrix} = t \begin{vmatrix} a & b \\ c & d \end{vmatrix} \)
■ 다음과 같이 임의의 행에 어떤 벡터를 더했을 때의 행렬식은 덧셈을 당한 행과 덧셈을 가하는 벡터로 분리하여 행렬식을 계산할 수 있다는 것이다. 이때 위의 공통 인수 특성에서 스칼라가 곱해진 행에서만 공통 인수를 빼낼 수 있었던 것처럼 덧셈 연산이 적용되지 않은 나머지 \( n - 1 \)의 행들은 그대로 두어야 한다는 것이다.
\( \begin{vmatrix} a + a' & b + b' \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a' & b' \\ c & d \end{vmatrix} \)
■ 그리고 이 특성이 \( \text{det} (A+B) = \det{(A)} + \det{(B)} \)를 의미하는 것은 아니다.
■ \( \text{det} (A+B) = \det{(A)} + \det{(B)} \)라는 것은 모든 행에 대해서 위와 같은 선형성이 동시에 적용된다는 것을 의미한다.
■ 행렬식의 정방행렬에서 '각각의' 행(또는 열)에 대해서만 독립적으로 선형성을 가진다. 즉, \( \text{det} (A+B) \neq \det{(A)} + \det{(B)} \)
■ 세 번째 특성을 이용하면, 다음과 같이 하나의 행렬식을 각각의 행에 대한 선형 결합으로 나타낼 수 있다.
\( \begin{vmatrix} t(a + a') & t(b + b') \\ c & d \end{vmatrix} = t \begin{vmatrix} a & b \\ c & d \end{vmatrix} + t \begin{vmatrix} a' & b' \\ c & d \end{vmatrix} \)
■ 행렬식의 3 가지 주요 특성을 정리하면 다음과 같다.
- ① \( \det A = \begin{vmatrix} 1 & 0 \\ 0 & 1 \end{vmatrix} = (1 - 0) = 1 \)
- ② 두 개의 행을 바꾸면, 행렬식의 값은 부호가 바뀐다.
- ③ \( \begin{vmatrix} ta & tb \\ c & d \end{vmatrix} = t \begin{vmatrix} a & b \\ c & d \end{vmatrix} \) & \( \begin{vmatrix} a + a' & b + b' \\ c & d \end{vmatrix} = \begin{vmatrix} a & b \\ c & d \end{vmatrix} + \begin{vmatrix} a' & b' \\ c & d \end{vmatrix} \)
■ 위와 같은 3가지 속성이 행렬식을 정의하는 속성. 즉, 반드시 지켜야 하는 성질이다.
1.2 행렬식의 나머지 특성
■ 4번 특성은 두 행이 같으면 행렬식 값이 0이 된다는 것이다.
■ 예를 들어 \( n \times n \) 정방 행렬에서 첫 번째 행과 세 번째 행이 같다고 가정해 보자. 이 첫 번째 행과 세 번째 행을 교환한다면, 두 행은 동일한 원소를 가지는 같은 행이므로 동일한 행렬을 얻어야 한다.
■ 하지만 2번째 성질에서 행 교환이 발생하면 행렬식 값의 부호가 바뀌게 된다. 이때, 부호가 바뀌지 않고 변하는 행렬식이 있으며 유일한 가능성은 행렬식이 0이라는 것이다. 0은 부호가 바뀌어도 0이다.
■ 그리고 (최소) \( n \times n \) 정방 행렬에서 두 개의 동일한 행(또는 열)이 있다는 것은 선형 종속임을 의미하며, 선형 종속이라는 것은 정방행렬의 rank가 full rank가 아님을 의미한다.
■ 정방 행렬 \( A \)에 대해 \( A \mathbf{x} = 0 \)에서 \( A \)의 역행렬이 존재하면 \( \mathbf{x} = A^{-1} 0 = 0 \)으로 \( \mathbf{x} \)는 0이라는 자명한 해만 가지게 된다.
■ \( A \)가 full rank가 아니라는 것은 일부 행(또는 열)들 간에 선형 종속성이 존재하여 영벡터가 아닌 \( \mathbf{x} \)가 \( A \mathbf{x} = 0 \)을 만족하게 되며, 이는 \( A \)의 선형 변환이 일대일 함수가 아님을 의미한다.
■ 역함수가 존재하려면 함수가 일대일 대응이어야 하듯, 역행렬이 존재하려면 \( A \)의 선형 변환이 일대일 함수여야 한다.
■ 정리하면, \( n \times n \) 정방 행렬에서 두 개의 동일한 행(또는 열)이 있다는 것은 선형 종속성이 존재함을 의미하며, 이는 정방행렬을 rank가 full rank가 아님을 의미한다. full rank가 아니라는 것은 \( A \mathbf{x} = 0 \)에서 \( \mathbf{x} \)가 자명해 \( \mathbf{x} = 0 \)를 가지지 않고, 영벡터가 아닌 다른 해들로 \( \mathbf{x} \)가 \( A \mathbf{x} = 0 \)을 만족한다는 것이며, 이는 \( A \)의 선형 변환이 일대일 함수가 아니므로 \( A \)는 역행렬이 아니다. \( A \)는 비가역행렬이다.라고 할 수 있다. 이때, 행렬식의 성질 중 두 개의 동일한 행(또는 열)이 존재하면 \( A \)의 행렬식 값은 0이 된다는 성질이 있다. 그러므로 \( n \times n \) 행렬 \( A \)에 대해 \( \det{(A)} = 0 \Leftrightarrow \) \( A \)는 비가역행렬이다.' 가 성립한다. 반대로, \( A \)가 full rank이면 역행렬이며, full rank라는 것은 정방 행렬 \( A \)의 모든 행(또는 열)이 선형 독립이라는 것이다. 이러한 \( A \)의 행렬식 값은 \( \neq 0 \)이므로 \( \det{(A)} \neq 0 \Leftrightarrow \) \( A \)는 가역행렬이다.' 가 성립한다.
\( \det{(A)} = 0 \Leftrightarrow \) \( A \)는 비가역행렬(=특이행렬 = 비정칙행렬)
\( \det{(A)} \neq 0 \Leftrightarrow \) \( A \)는 가역행렬(=비특이행렬 = 정칙행렬)
■ 5번째 특성은 하나의 행에 실수를 곱하여 다른 행에 더하거나 빼도, 행렬식 값은 변하지 않는다. 즉, 일련의 소거 과정을 거친 행렬의 행렬식 값과 원래 행렬의 행렬식 값은 같다.
■ 예를 들어 다음과 같이 첫 번째 행에 \( l \)을 곱하여 두 번째 행에 뺄셈을 했을 때
\(
\begin{vmatrix} a & b \\ c - \ell a & d - \ell b \end{vmatrix}
= \begin{vmatrix} a & b \\ c & d \end{vmatrix}
+ \begin{vmatrix} a & b \\ -\ell a & -\ell b \end{vmatrix}
\)
\(
a(d - \ell b) - b(c - \ell a) = ad - bc + (-\ell ba + \ell ab)
\)
세 번째 특성에 의하여 위와 같이 행렬식을 분리할 수 있다. 이때 분리된 행렬식 중 맨 우측의 행렬식 값은 0이 되므로 원래 행렬의 행렬식 값과 같아지는 것을 알 수 있다.
■ 혹은 세 번째 특성 중 공통 인수를 행렬식 밖으로 빼낼 수 있다는 성질과 네 번째 성질을 이용하여 다음과 같이 원래 행렬의 행렬식 값과 소거 과정을 거친 행렬의 행렬식 값이 동일함을 확인할 수도 있다.
\(
\begin{vmatrix} a & b \\ c - \ell a & d - \ell b \end{vmatrix}
= \begin{vmatrix} a & b \\ c & d \end{vmatrix}
- \ell \begin{vmatrix} a & b \\ a & b \end{vmatrix}
\)
\(
a(d - \ell b) - b(c - \ell a) = ad - bc - \ell (ab + ba)
\)
맨 우측의 두 행이 동일한 행이므로 네 번째 특성에 의해 맨 우측의 행렬식 값은 0이 된다.
■ 6번째 특성은 모든 원소(성분)이 0으로 구성된 행이 하나라도 존재하면, 해당 행렬의 행렬식 값은 0이다.
■ 예를 들어 다음과 같이 첫 번째 행의 원소가 0이라면, 첫 번째 행의 공통 인수는 0이므로 행렬식 밖으로 빼낼 수 있으므로 행렬식 값은 0이 된다.
\(
\begin{vmatrix} 0 \times a & 0 \times b \\ c & d \end{vmatrix}
= 0 \begin{vmatrix} a & b \\ c & d \end{vmatrix}
\)
■ 혹은 동일한 두 행이 있으면 행렬식 값은 0이 된다라는 성질과 하나의 행에 실수를 곱하여 다른 행에 더하거나 빼도, 행렬식 값은 변하지 않는 성질을 이용해서 6번째 특성을 유도할 수도 있다.
■ \( n \times n \) 행렬에서 첫 번째 행과 세 번째 행이 동일하다면, 첫 번째 행에 -1을 곱해 세 번째 행에서 빼면 세 번째 행을 구성하는 원소(성분)은 모두 0이된다.
■ 이때 \( n \times n \) 행렬에서 두 행이 동일하다면 행렬식 값은 0이며, 하나의 행에 실수를 곱하여 다른 행에 더하거나 빼도, 행렬식 값은 변하지 않으므로 세 번째 행의 원소가 모두 0인 행렬식 값은 0이 된다.
\(
\begin{vmatrix}
a & b & c & d \\
e & f & g & h \\
a & b & c & d
\end{vmatrix}
=
\begin{vmatrix}
a & b & c & d \\
e & f & g & h \\
0 & 0 & 0 & 0
\end{vmatrix}
= 0
\)
■ 이 역시 행렬식 값이 0이므로 한 행의 원소가 모두 0인 행렬은 비가역행렬이다. 라고 할 수 있다.
■ 7번째 특성은 상삼각행렬과 관련되어 있다. 예를 들어 \( n \times n \) 정방행렬이 다음과 같은 상삼각행렬이라면
\(
U = \begin{bmatrix}
d_1 & * & * & * \\
0 & d_2 & * & * \\
0 & 0 & \ddots & * \\
0 & 0 & 0 & d_n
\end{bmatrix}
\)
상삼각행렬 \( U \)의 행렬식 값은 \( U \)의 주대각원소들의 곱이다.
\(
\det U = \begin{vmatrix}
d_1 & * & * & * \\
0 & d_2 & * & * \\
0 & 0 & \ddots & * \\
0 & 0 & 0 & d_n
\end{vmatrix}
= d_1 \times d_2 \times \cdots \times d_n
\)
■ \( U \)에서 주대각원소 위에 있는 원소들이 행렬식 값에 영향을 미치지 않는 이유(=상삼각행렬의 행렬식 값이 주대각원소들의 곱인 이유)는 위쪽 방향으로 소거를 진행하여 \( U \)행렬의 주대각원소 위에 있는 원소들을 0으로 만들어서. 즉, \( U \)를 대각 행렬 \( D \)로 만들었을 때 대각 행렬 \( D \)의 행렬식 값도 다음과 같이 주대각원소들의 곱이기 때문이다.
\(
\det D = \begin{vmatrix}
d_1 & 0 & 0 & 0 \\
0 & d_2 & 0 & 0 \\
0 & 0 & \ddots & 0 \\
0 & 0 & 0 & d_n
\end{vmatrix}
= d_1 \times d_2 \times \cdots \times d_n
\)
이를 통해 \( U \)의 주대각원소 위에 있는 원소들이 행렬식 값에 영향을 미치지 않는다는 것을 알 수 있다.
■ 이러한 상삼각행렬과 대각행렬의 행렬식 값이 주대각원소들의 곱이 되는 이유는 다음과 같다.
■ 대각행렬의 행렬식에서 공통 인수를 빼낼 수 있다는 성질을 이용하면, 각 행의 공통 인수를 하나씩 빼낼 수 있으며, 이는 행렬식 밖에서 \( d_1 \times d_2 \times \cdots \times d_n \)이 된다.
■ 이렇게 공통 인수를 빼내면 다음과 같이 원래 행렬식은 단위행렬의 행렬식이 된다.
\(
\det D = \begin{vmatrix}
d_1 & 0 & 0 & 0 \\
0 & d_2 & 0 & 0 \\
0 & 0 & \ddots & 0 \\
0 & 0 & 0 & d_n
\end{vmatrix}
= d_1 \times d_2 \times \cdots \times d_n
\)
\(
\det D = d_n \cdots d_2 d_1
\begin{vmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \ddots & 0 \\
0 & 0 & 0 & 1
\end{vmatrix}
= d_n \cdots d_2 d_1 \times 1
\)
■ 첫 번째 성질에 의해 단위행렬의 행렬식 값은 1이므로 대각행렬의 행렬식 값은 주대각원소들의 곱이 된다. 그리고 이는 상삼각행렬의 행렬식 값이 주대각원소들의 곱인 이유와 같은 논지이므로, 상삼각행렬과 대각행렬의 행렬식 값은 주대각원소들의 곱이라고 할 수 있다.
■ 위의 대각행렬의 행렬식 값이 계산되는 과정을 보면, 단위행렬이 있다. 단위행렬은 항상 가역행렬이라는 것이다.
■ 즉, \( n \times n \) 정방행렬 \( A \)가 가역행렬이라면(= 행렬식 값 \( \neq 0 \) = 행렬의 각 행(또는 열)이 선형 독립), 다음과 같이 \( A \)의 행연산을 통해 상삼각행렬(또는 대각행렬)로 만들어 행렬식 값을 주대각원소들의 곱으로 계산할 수 있다.

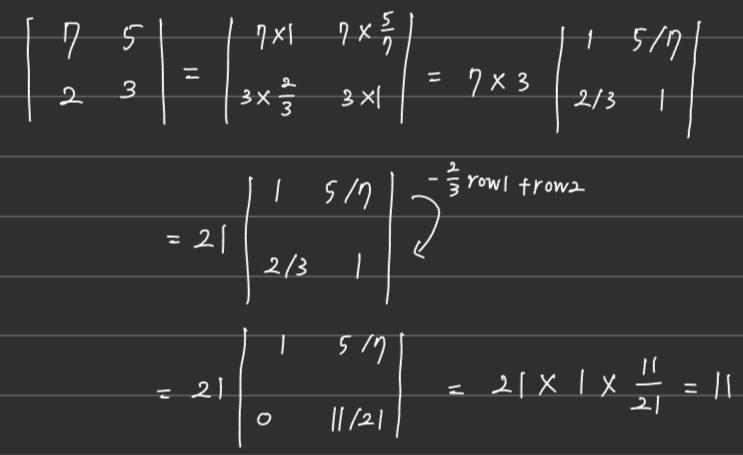
cf) \( n \times n \) 정방행렬을 위와 같이 상삼각행렬로 바꾸게 되면 행렬식 값은 주대각원소들의 곱이기 때문에 원래 행렬에서 행렬식 값을 계산하는 것보다 훨씬 빨리 계산할 수 있다.
■ 8번째 특성은 \( n \times n \) 행렬 \( A \)가 특이행렬(singular matirx)라면 행렬식 값은 0이고, 특이행렬이 아니라면 행렬식값이 0이 아니다.
- 이는 앞서 언급한, 행렬식 값 \( \neq 0 \Leftrightarrow \) \( A \)는 가역행렬
- 행렬식 값 \( = 0 \Leftrightarrow \) \( A \)는 비가역행렬
■ 역행렬이 존재하려면 행렬 \( A \)는 정방행렬이고 full rank이다. \( \text{rank} = n \)
- 역행렬 \( A^{-1} \)의 정의는(혹은 행렬 \( A \)의 역행렬이 존재하면) \( A^A{-1} = A^{-1}A = I \)이다.
- 이때, 단위 행렬 \( I \)는 반드시 \( n \times n \) 정방 행렬이다. 즉, 행렬곱 \( A^A{-1} \)나 \( A^{-1}A \)는 \( n \times n \)이어야 한다. 그러므로 이를 만족하는 행렬 \( A \)의 크기는 \( n \times n \)이어야 한다.
- 행렬 \( A \)의 원소가 \( a \), \( \mathbf{x} \)의 원소가 \( x \)라고 할 때,
- \( A \mathbf{x} = 0 \)은 행렬 \( A \)가 \( m \times n \)이면,
- \( A \)의 첫 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{11} + x_2 a_{12} + \cdots x_n a_{1n} = 0 \),
- 두 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{21} + x_2 a_{22} + \cdots x_n a_{2n} = 0 \),
- \( m \) 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{m1} + x_2 a_{m2} + \cdots x_n a_{mn} = 0 \)이 되어야 한다.
- 행렬 \( A \)가 \( n \times n \)이라고 해도
- 첫 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{11} + x_2 a_{12} + \cdots x_n a_{1n} = 0 \), 두 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{21} + x_2 a_{22} + \cdots x_n a_{2n} = 0 \), \( n \) 번째 행과 벡터 \( \mathbf{x} \)의 곱은 \( x_1 a_{n1} + x_2 a_{n2} + \cdots x_n a_{nn} = 0 \)이 되어야 한다.
- 이때, 행렬 \( A \)에서 종속 관계가 있다면 full rank를 가지지 못하므로 free column이 존재하여 free variable을 통해, \( \mathbf{x} = x_1, x_2, \cdots, x_n \)의 모든 원소가 0이 아닌 위의 선형 결합을 만족하는 \( \mathbf{x} \)를 찾을 수 있다.
- 하지만, 행렬 \( A \)가 독립 관계라면 \( \text{rank} A = n \). 즉, full rank이므로 어떠한 free column이 존재하지 않는다. free variable이 존재하지 않는 상황에서 위의 선형 결합을 만족하려면, \( \mathbf{x} \)는 \( \mathbf{x} \)의 모든 원소가 0이 되어야 한다.
- 그러므로 \( A \)가 full rank라면 \( \mathbf{x} = 0 \)으로 영벡터를 유일해로 갖게 된다.
- \( \mathbf{x} = 0 \)으로 영벡터를 유일해로 갖게 된다는 것은 \( N(A) = \left\{ 0 \right\} \)이며, 퇴화차수 정리 \( \text{rank} (A) + N(A) = n \)에 의해 \( \text{rank} A + 0 = n \)으로 다시 한번, \( A \)가 full rank임을 확인할 수 있다.
- 행렬 \( A \)가 full rank라는 조건 하에서 가우스-조단 소거법을 사용해 행렬 \( A \)를 단위행렬 \( I \)로 바꿀 수 있으며, 이때 수행되는 기본 행연산을 동일하게 \( I \)에 적용하면 \( A^{-1} \)를 얻을 수 있다.
- 즉, \( [A \mid I] \Longrightarrow [I \mid A^{-1}] \)을 통해 \( A \)가 full rank라는 조건 하에 가우스-조단 소거법을 통해 \( A^{-1} \)가 존재하는 것을 보일 수 있다.
- 이렇게 역행렬이 존재하려면 정방행렬이어야 하며, 행렬의 영공간이 오직 영벡터만을 포함하도록 행렬의 rank가 full rank여야 한다.
■ 행렬 \( A \)의 벡터들이 선형 독립인 관계. 즉, full rank이면 어떠한 연산을 해도 행렬식 값이 0이 되지 않는다. 행렬식 값이 0이 되려면 벡터들이 종속 관계. 즉, 서로 다른 벡터가 스칼라배 관계여야 하기 때문이다.
■ 그러므로 \( \det{(A)} \neq 0 \Leftrightarrow A \text{ is invertible} \)이 성립하는 것이다.
■ 역행렬이 존재하지 않는 경우는 위와 반대인 경우이다. 행렬 \( A \)가 full rank가 아니어야 하며, 이는 \( A \)의 벡터들이 종속 관계에 있음을 의미한다.
■ 행렬 \( A \)의 벡터들이 종속 관계에 있을 때, 행렬을 소거하면 어떤 피벗 원소가 0이 된다. 그리고 원소가 0인 피벗의 개수만큼 행렬의 rank가 줄어들게 된다.
■ \( n \times n \) 행렬 \( A \)의 계수(rank)가 \( \text{rank} < n \)이라는 것은, free variable이 존재함을 의미하며, 소거법을 적용한 결과 최소한 한 개 이상의 행에서 행의 모든 원소가 0이라는 것을 의미한다.
■ 행렬식의 성질 중 모든 행의 원소가 0이면 행렬식 값은 0이 된다. 혹은 행렬에 동일한 원소를 갖는 벡터(또는 스칼라배 관계를 갖는 벡터)가 존재하면 해당 행렬식 값은 0이 된다. 서로 다른 벡터가 스칼라배 관계라는 것은 두 벡터의 관계가 종속임을 의미한다.
■ 그러므로 \( \det{(A)} = 0 \Leftrightarrow A \text{ is singular matrix} \)가 성립하는 것이다.
■ 행렬 \( A \)가 역행렬을 가진다면, 위의 예시와 같이 소거를 통해 \( A \)를 상삼각행렬 \( U \)로 만든 다음, 다시 위쪽 방향으로 소거를 진행하여 대각행렬 \( D \)를 만들고, 대각행렬의 행렬식 값은 대각행렬의 주대각원소들의 곱이라는 점을 이용하여 행렬 \( A \)의 행렬식 값을 구할 수 있다.

■ 그리고 이 과정에서 \( 2 times 2 \) 크기를 갖는 정방행렬의 행렬식 계산 공식 \( ad-bc \)가 유도된다. 행렬 \( A \)가 \(
A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
\)이고 \( a \neq 0 \)이라면
\(
A = \begin{bmatrix} \boxed{a} & b \\ c & d \end{bmatrix}
= \begin{bmatrix} \boxed{a} & b \\ c - \frac{c}{a} a & d - \frac{c}{a} b \end{bmatrix}
= \begin{bmatrix} \boxed{a} & b \\ 0 & d - \frac{c}{a} b \end{bmatrix} = U
\), \(
\quad a \left( d - \frac{c}{a} b \right) = ad - bc
\)
- \( a \)가 0이 아니므로 \( -bc \)가 아닌 \( ad - bc \)가 성립한다.
- \( a \)가 바로 원소가 0이 아닌 피벗이다.
- 만약 \( a \)가 0이었다면, 행 교환을 해야한다. 행렬식이므로 행 교환 시 행렬식의 부호가 바뀐다.
- 행 교환을 통해서도 계산할 수 없다면 \( A \)가 바로 특이 행렬(singular matrix)이다.
■ 9번째 특성은 \( \det{AB} = \det{A} \det{B} \)이다. 행렬 \( A \)와 \( B \)의 곱의 행렬식은 \( A \)의 행렬식과 \( B \)의 행렬식의 곱과 같다.
■ 행렬식은 선형성을 가지고 있지 않고, 덧셈 속성을 가지고 있지 않다. \( \text{det} (A+B) \neq \det{(A)} + \det{(B)} \)
■ \( A + B \)의 행렬식은 행렬식들의 합이 아니지만, \( A \times B \)의 행렬식은 행렬식들의 곱이다.
■ 예를 들어 A의 역행렬에 대한 행렬식 \( \det{A^{-1}} \)을 정의해 보자.
■ \( A \)의 역행렬이 존재한다면 \( A^{-1}A = I \)이다. 9번째 특성에 따르면 \( A^{-1}A = I \)의 양변에 행렬식을 씌울 경우 \( \det{A^{-1}A} = \det{A^{-1}} \det{A} = det{I} = 1 \)이 된다. 여기서 양변을 \( \det{A} \)로 나누면 \(
(\det A^{-1}) = \dfrac{1}{\det A}
\)이 된다.
■ \(
(\det A^{-1}) = (\dfrac{1}{\det A})
\)으로 \( A \)의 역행렬인 \( A^{-1} \)의 행렬식 \( \det{A^{-1}} \)은 \( \dfrac{1}{\det{A}} \)라고 할 수 있다.
■ \(
(\det A^{-1}) = (\dfrac{1}{\det A})
\)가 성립하는 \( A \)는 다음과 같이 대각행렬이 있다.
\(
A = \begin{bmatrix} 2 & 0 \\ 0 & 3 \end{bmatrix}, \quad
A^{-1} = \begin{bmatrix} \dfrac{1}{2} & 0 \\ 0 & \dfrac{1}{3} \end{bmatrix}
\)
\(
\det A = 6, \quad \det A^{-1} = \dfrac{1}{6}
\)
■ 그러므로 \( \det{A^{-1}A} = \det{A^{-1}} \det{A} = det{I} = 1 \Leftrightarrow \det{A^{-1}} = \dfrac{1}{\det{A}} \)가 성립하기 위해선 \( A \)가 대각행렬이 아닐 경우 \( A \)를 소거하여 상삼각행렬 \( U \)로 만들고, 다시 위쪽 방향으로 소거를 진행해서 대각행렬 \( D \)를 만들어야 한다.
■ 그리고 \(
(\det A^{-1}) = \dfrac{1}{\det A}
\)로 역행렬의 존재 여부를 판별할 수 있다. 행렬 \( A \)가 가역행렬이면 행렬식 값은 \( \neq 0 \)이므로 이 관계가 성립한다. 반면, \( A \)가 비가역행렬이면 행렬식 값은 \( = 0 \)이 된다. 이때 \(
\det A^{-1} = \dfrac{1}{0}
\)이 되므로 관계가 더 이상 성립하지 않는다.
■ 이번에는 동일한 행렬을 두 번 곱했을 때의 행렬식이다. \( AA \)에 행렬식을 씌웠을 때, 9번째 특성에 따르면 \( \det{AB} = \det{A} \det{B} \)이므로 \(
\det A^2 = \left( \det A \right) \left( \det A \right)
\)가 된다. 그리고 이것은 다시 다음과 같이 나타낼 수 있다.
\(
\det A^2 = \left( \det A \right) \left( \det A \right) = (\det A)^2
\)
■ 이번에는 \( n \times n \)행렬 \( A \)에 2를 곱한 경우, \( \det{2A} = 2^n \det{A} \)가 된다.
■ \( 2A \)는 \( n \times n \) 크기의 행렬 \( A \)의 첫 번째 행, 두 번째 행 , ... , \( n \)번째 행에 2를 곱한 행렬이다. 행렬식 성질 중 공통 인수를 행렬식 밖으로 빼낼 수 있다는 성질이 있다.
■ 이 성질을 이용하면 첫 번째 행에서 공통인수 2, 두 번째 행에서 공통인수 2, ... , \( n \) 번째 행에서 공통인수 2를 행렬식 밖으로 빼낸 것. 즉 \( n \)개의 2를 행렬식 밖으로 빼낸 것이며 이 값들은 곱해지므로 \( 2^n \)이 된다.
■ 그러므로 \( n \times n \)행렬 \( A \)와 임의의 상수 \( k \)에 대해 다음이 성립한다고 할 수 있다.
\( \det{kA} = k^n \det{A} \)
■ 이것은 부피와 같다. 행렬식 값은 어떤 숫자 값이라는 것을 고려했을 때, 예를 들어 어떤 상자의 모든 변을 2배로 하면 부피를 2의 \( n \) 승으로 곱하는 것과 같다. 만약 3차원 상자라면 부피는 8로 곱한다.
■ 10번째 특성은 \( \det{A^T} = \det{A} \)이다. \( A \)가 \( n \times n \)의 정방행렬이라면 다음과 같이 원래 행렬에 전치를 적용해도 가로와 세로의 크기는 변하지 않는다. 단, 행과 열이 바뀌게 된다.
\(
\begin{vmatrix} a & b \\ c & d \end{vmatrix}
=
\begin{vmatrix} a & c \\ b & d \end{vmatrix}
\)
■ 위와 같이 전치를 해도 행렬식 값의 계산은 둘 다 \( ad - bc \)이다. 그러므로 \(
|A^T| = |A|
\)
■ \(
|A^T| = |A|
\)에서 행렬 \( A \)에 소거를 진행하여 \( LU \)로 분해한다면 \(
|A^T| = |A| \rightarrow |U^T L^T| = |LU|
\)가 된다. 여기서 \( \det{AB} = \det{A} \det{B} \)를 이용하면 \(
|A^T| = |A| \rightarrow |U^T L^T| = |LU| \rightarrow |U^T||L^T| = |L||U|
\)가 된다. 이때 하삼각행렬 \( L \)은 대각 원소가 1로 이루어져 있으므로 \( L \)의 행렬식값은 주대각원소들의 곱으로 1이 된다.
■ 그러므로 \( |A^T| = |A| \rightarrow |U^T| = |U| \)가 성립한다. 이때 \( U \)도 상'삼각행렬'이므로 행렬식 값은 주대각원소들의 곱이다. 그리고 정방 행렬을 전치했을 때 주대각원소의 값이 변하지는 않는다. 그러므로 \( IU^T| = |U| \)는 성립한다.
'선형대수' 카테고리의 다른 글
| [개념] 선형 변환(사상)과 표준행렬 (0) | 2025.02.16 |
|---|---|
| Cramer's rule, inverse matrix, and volume (0) | 2025.02.10 |
| Orthogonal matrices and Gram-Schmidt (0) | 2025.02.10 |
| Projection matrices and least squares (0) | 2025.02.10 |
| Projections onto subspaces (0) | 2025.02.10 |



