1. Projection - Two extreme cases
■ 투영 행렬 P=A(ATA)−1AT는 Ax=b의 우변 벡터 b를 A의 열공간에서 가장 가까운(근사한) 벡터로 바꿔주는 역할을 한다.
■ 그러므로 P에 b를 곱하면 벡터 b를 열공간에서 가장 가까운 벡터 p로 투영한다. p=Pb
■ 여기서 말하는 두 가지 극단적인 경우는 벡터 b가 이미 A의 열공간에 존재하는 경우와 벡터 b가 열공간에 수직인 경우이며, 두 가지 경우의 벡터 b에 투영 행렬 P를 곱했을 때 어떤 결과가 발생하는지 확인하려 한다.
■ 먼저 벡터 b가 열공간에 존재하는 경우 투영 행렬 P에 b를 곱하면, 다시 b를 얻는다. 즉, Pb=b
■ 벡터 b가 열공간에 존재하는 벡터라는 것은 A의 열벡터들의 선형 결합으로 벡터 b를 만들 수 있다는 것이며, Ax=b이므로 여기서의 선형 결합은 Ax이다.
■ 벡터 b가 열공간에 존재하는 경우 Ax=b가 성립한다. 이때 투영 행렬 P=A(ATA)−1AT에 b를 곱하면 Pb=A(ATA)−1ATAx=Ax=b가 성립하게 된다. 이는 투영 행렬이 이미 열공간에 존재하는 벡터 b를 그대로 유지시킨 것으로 볼 수 있다.
■ 두 번째 경우는 벡터 b가 열공간에 수직인 경우이다. 열공간을 어떤 평면이라고 생각했을 때, 열공간이 벡터 b와 수직이라는 것은 벡터 b와 평면의 모든 벡터들의 내적 결과가 0이라는 것을 의미한다.
■ A의 대표적인 열공간의 벡터는 열공간의 기저이며 Ax=b에서 b는 열벡터이고 A의 열은 AT에서 행으로 바뀌므로,
■ ATb는 b와 수직인 벡터들(여기서는 A의 기저)과 b의 내적들의 계산을 하는 것이므로 ATb=0이 성립한다.
■ P=A(ATA)−1AT에 벡터 b를 곱하면 Pb=A(ATA)−1ATb이며 ATb=0이므로 Pb=A(ATA)−1ATb=0이 성립한다.
■ 또한, b가 열공간과 수직이라는 것은 b가 열공간이 아닌 다른 공간에 존재한다는 것을 의미한다. 바로 left null space에 벡터 b가 존대한다. 다음과 같이 열공간과 수직인 공간은 left nullspace이기 때문이다.

■ 열공간과 left nullspace는 서로 직교하므로 열공간에 있는 모든 벡터와 left nullspace에 있는 모든 벡터들의 내적은 0이 되어야 한다.
■ 여기서 알 수 있는 것은 p는 열공간에 있는 b와 근사한 벡터이다. 즉, p는 열공간에 존재한다.
■ 그리고 오차 벡터 e는 p와 직교한다. p는 열공간에 있기 때문에 p와 수직 관계를 갖는 e는 left nullspace에 존재한다.
■ 그리고 벡터 b는 위의 두 극단적인 경우처럼, 열공간에 존재하거나 left nullspace에 존재할 수 있으며, 열공간과 left nullspace의 교집합에 있을 수도 있다.
■ 만약, 다음과 같이 벡터 p는 열공간에, 벡터 e는 left nullspace에 존재하는데 벡터 b가 열공간에 존재하지 않는 경우

벡터 b를 열공간에 투영한 벡터가 p가 되고 left nullspace에 투영한 벡터가 e가 되는 것을 알 수 있다.
■ p는 벡터 b를 열공간에 투영한 것이기 때문에 p=Pb가 된다. b=p+e임을 이용하면, b=Pb+e⇔e=b−Pb=(I−P)b가 성립한다. 즉 오차 벡터 e는 I−P라는 투영 행렬에 벡터 b를 곱한 결과로 볼 수 있다.
- (I−P)도 투영 행렬이기 때문에 (I−P)T=(I−P)와 (I−P)2=(I−P)를 만족한다.
■ p=Pb와 e=(I−P)b임을 이용하면, b=p+e는 다음과 같이 전개되므로 b=p+e=b가 된다.
b=p+e=Pb+(I−P)b=Pb+Ib−Pb=b
2. Least Square Method(최소자승법 또는 최소제곱법)
■ 투영(projection)을 사용하는 이유는 Ax=b에서 미지수보다 방정식이 많아서 해가 존재하지 않을 때, 정확한 해가 아니더라도 주어진 모든 방정식을 최대한 만족시키는 근사해(또는 최적해)를 찾기 위함이다.
■ Least Square Method는 주어진 정보(방정식)를 최대한 만족시키는 하나의 직선 방정식을 찾는 방법이다.
- 즉, 최소자승법(최소제곱법)의 가설은 직선 방정식 y=ax+b가 된다.
■ 예를 들어 다음과 같이 가로 축이 시간에 대한 축이고 세로 축이 시간에 따른 점수를 나타내는 축이라고 했을 때, 1시간에 1점, 2시간에 2점, 3시간에 2점을 받았다고 하자.

■ 이렇게 주어진 정보 (1, 1), (2, 2), (3, 2)를 이용해 미래 시점에 발생하는, 4시간, 5시간일 때 받을 수 있는 점수를 예측하기 위해 최소자승법은 위의 데이터 포인트들을 잘 표현할 수 있는 하나의 최적의 직선을 찾는다.
■ 최소자승법의 가설은 직선의 방정식 y=ax+b이기 때문에, 위의 데이터들을 잘 표현할 수 있는 최적의 직선을 찾는 문제는 최적의 a,b를 구하는 문제가 된다.
■ 문제를 푸는 방법은 다음과 같이 최소자승법의 가설인 y=ax+b에 주어진 정보 (x,y)=(1,1),(2,2),(3,2)를 넣는다. 넣으면, 방정식을 얻을 수 있으며, 방정식을 Ax=b형태로 바꿀 수 있다.
[112131][ab]=[122]
■ 이 에에서 미지수보다 방정식이 더 많으므로( 행렬 A가 m > n )) Ax=b를 완벽하게 만족시키는 정확한 해 x는 존재하지 않는다.
■ 그러므로 다음과 같이 근사해(또는 최적해)를 구하기 위해 Ax=b의 양변에 AT를 곱해 ATAˆx=ATb를 계산하면 된다.
■ 현재 찾고자 하는 직선은 주어진 데이터를 잘 표현할 수 있는 최적의 직선이며, 데이터를 잘 표현하는 직선은 실제값과 예측값의 오차(error)가 최소가 되게 만드는 직선을 의미하며, 결국 각 데이터와 직선 사이의 오차에 대해 오차의 총합이 최소가 되게 만드는 직선의 파라미터 a,b를 찾아야 한다.
■ 이상적인 경우는 모든 오차가 0이 되는 상황이다. Ax는 주어진 데이터를 직선 y=ax+b에 대입한 상태이며, 우변 b는 그 결과인 y이므로 모든 오차가 0이 되는 상황은 Ax−b=0이다.
■ 즉, 오차 벡터를 e라고 했을 때, Ax−b=e이며, 최소화 하고자 하는 것은 오차'값'이므로 Ax−b=e에 norm을 씌워야 한다. 그리고 오차 결과가 음수가 나오는 것을 방지하기 위해서 다음과 같이 제곱을 해야 한다.
‖Ax−b‖2=‖e‖2
■ 그러므로 최소자승법은 Minimize ‖Ax−b‖2=‖e‖2를 푸는 문제가 된다. (정확히는 목적 함수를 최소화하는 파라미터를 찾기 위함)
- Ax−b의 결과는 오차 벡터 e이며, 오차 벡터에 대한 길이는 오차의 총 크기를 나타낸다.
■ 만약 다음과 같이 최적의 직선을 찾았을 때, 기존의 데이터와 직선의 거리가 가까우면 오차가 적은 것이며, 거리가 멀면 오차가 큰 상황이다.

- 이 예에서는 다음과 같이 오차 e1,e2,e3를 얻었다고 하자.
■ 위의 그림은 주어진 데이터를 이용해 직선의 파라미터 a,b를 추정해서 t−s평면에 그린 그림이다. 하얀색 점은 실제값, 파란색 점은 예측값이며, 빨간색 선은 실제값과 예측값이 차이. 즉, 오차를 나타낸다.
■ 오차 벡터를 e=[e1,e2,e3]T라고 했을 때, 오차의 총합은 각 오차의 자승(square)의 합으로 표현할 수 있다. overall error=e21+e22+e23
■ overall error=e21+e22+e23 이 값이 최소화하고자 하는 오차(손실)값이다.
2.1 Outliers in Least Square
■ 이상치(outlier)란, 데이터들의 분포에서 크게 벗어난 소수의 데이터를 의미한다. 이러한 outlier는 대부분 쓸모없는 값. 즉, noise data인 경우가 많다.
■ 최소자승법은 모든 데이터에 대한 오차를 최소화해야 하는데 만약 다음과 같이 (0, 3)의 outlier가 추가 된다면, outlier의 영향을 크게 받아 직선의 파라미터값이 바뀔 것이다.(직선의 형태가 바뀐다.)
■ 즉, outlier가 존재하면 최소자승법은 전체 데이터를 잘 반영하지 못하게 될 가능성이 커진다.
2.2 Solution of Least Square
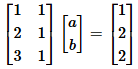
■ 이 문제는 앞서 얘기한 것처럼 ATAˆx=ATb를 계산하면 된다.
■ ATAˆx=ATb를 계산하면 [14663][ˆaˆb]=[115] [146]ˆa+[63]ˆb=[115]이므로 계산하면 ˆa=12,ˆb=23이므로 최적의 직선 방정식은 y=12x+23이 된다.
- 좌변을 우변으로 넘겨 풀 수 도 있는데. 즉 ˆx에 대한 식으로 정리할 수 있는데, 이는 ATA의 역행렬이 존재해야 한다는 조건이 있다.
- ATA의 역행렬이 존재하는 조건은 A의 열벡터들이 독립이어야 한다는 것이며, 앞서 rankA=rankATA와 N(A)=N(ATA)가 성립함을 확인하였다.
■ 다음 문제에서 순서대로 A,x,b라고 한다면,
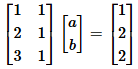
■ 행렬 A의 열벡터는 독립이므로 두 열벡터는 행렬 A의 열공간의 기저이다.
■ 그리고 b는 해가 존재하지 않는 상황이므로 열공간에 존재하지 않는다.
■ 이렇게 정확한 해는 존재하지 않지만 최대한 유사한 해를 구하기 위해 투영을 사용한다. 정확히는 b를 열공간에 투영시킨다.
■ b를 열공간에 투영시켜 얻은 벡터를 p라고 한다면, b=[122]T에서 p=[p1,p2,p3]T으로 바꾼 것이며 Ax=b의 문제는 Aˆx=p를 푸는 문제가 된다.
[112131][ˆaˆb]=[p1p2p3]
■ 여기서 얻은 p1,p2,p3이 바로 최적의 직선을 통해 계산한 '예측값'이다.
■ 위에서 구한 ˆa=12,ˆb=23를 위에 넣으면 p1=76,p2=53.p3=136이며, p=[p1p2p3]T를 통해 e=b−p임을 이용하여 오차 벡터 e를 다음과 같이 구할 수 있다. 여기서 얻은 e1,e2,e3이 각 포인트에서의 오차값이다. e=[122]−[7653136]=[−1626−16] ■ 이와 같은 최소자승법은 통계학에서 회귀(= 관찰된 연속형 변수들에 대해 두 변수 사이의 모형을 구한 뒤 적합도를 측정)이며, 찾고자 하는 것은 최적의 직선. 즉 선형이므로, 최소자승법은 통계학의 선형 회귀(Linear Regression)과 같다.
2.3 error vector
■ 원래 값인 b는 오차 벡터 e와 투영 벡터 p의 합으로 표현된다. 그리고 p는 열공간에 e는 left nullspace에 있기 때문에 p와 e는 직교한다.
b=[122]=e+p=[−1626−16]+[76106136]
■ 위에서 계산한 p와 e를 내적하면 -7/36 + 20/36 - 13/36 = 0이 된다.
■ 단, e와 직교하는 것은 p만 있는 것이 아니다. 열공간에는 p와 행렬 A의 열공간을 생성하는 열공간의 기저도 포함되어 있다. 즉, left nullspace에 있는 e는 열공간의 모든 벡터와 직교하므로 행렬 A의 열공간의 기저와도 직교한다.
- 행렬 A의 열공간의 기저 두 개를 a1,a2라고 했을 때, 오차 벡터 e와의 내적 eTa1과 eTa2를 계산하면 eTa1=0, eTa2=0이 되는 것을 확인할 수 있다.
'선형대수' 카테고리의 다른 글
| Properties of determinants (0) | 2025.02.10 |
|---|---|
| Orthogonal matrices and Gram-Schmidt (0) | 2025.02.10 |
| Projections onto subspaces (0) | 2025.02.10 |
| Orthogonal vectors and subspaces (0) | 2025.02.10 |
| Matrix spaces; rank 1 (0) | 2025.02.04 |



