Projections onto subspaces

■ 투영행렬(projection matrix)을 알기 위해선 먼저 해가 존재하지 않는 선형연립방정식의 해를 구하는 방법을 알아야 한다. 정확히는 애초에 해가 없으므로 정확한 해를 구한다기 보다는 가장 근사한 해를 구하는 방법이다.

- 이렇게 정확한 해가 없는 상태에서 가장 근사한 해를 구하는 것은 최소자승법(least square method), 투영행렬과 관련이 있다.

1. Solving $Ax = b$ when there is no solutin 

■ $A \mathbf{x} = b$에서 행렬 $A$의 열공간에 우변 $b$가 존재하면 가해 조건을 만족하므로 해를 구할 수 있다. 

■ 반면, $A \mathbf{x} = b$에서 행렬 $A$의 열공간에 우변 $b$가 존재하지 않는다면 가해 조건을 만족하지 않으므로 해가 존재하지 않는 경우로 분류된다.

■ $m \times n$ 행렬 $A$에서 $A \mathbf{x} = b$는 미지수의 개수 $n$보다 방정식의 개수 $m$이 더 많은 경우 ($m > n$), 행렬 $A$의 rank는 $m$보다 작고 최소 $n$이 된다. 이런 경우 열벡터의 차원이 rank보다 작기 때문에 $A \mathbf{x} = b$를 만족하는 해 $mathbf{x}$가 존재하지 않을 수 있다.

■ 이렇게 미지수보다 방정식의 수가 많은 경우 ($m > n$)를 'overdetermined', 미지수와 방정식의 수가 같은 경우 ($m = n$)를 'determined', 방정식이 미지수보다 적은 경우 ($m < n$)를 'underdetermined'라고 부른다.

■ 예를 들어

- overdetermined인 경우는 다음과 같으며, 대부분의 경우 해가 존재하지 않는다.

$Ax = b \quad \rightarrow \quad \begin{bmatrix}  2 & 3 & 5 \\  1 & 6 & 2 \\  4 & 8 & 7 \\  5 & 1 & 3  \end{bmatrix} \begin{bmatrix}  x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}  10 \\ -3 \\ 15 \\ 7 \end{bmatrix} \quad (m=4 > n=3)$

- determined인 경우는 다음과 같으며, '정확한 해'가 존재한다.

$Ax = b \quad \rightarrow \quad \begin{bmatrix}  3 & 2 & 4 \\  5 & 7 & 1 \\  6 & 2 & 8  \end{bmatrix} \begin{bmatrix}  x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}  9 \\ -5 \\ 12 \end{bmatrix} \quad (m=3 = n=3)$

- underdetermined인 경우는 다음과 같으며 무수히 많은 해를 갖는다. 그리고 $A$가 full rank라면 '유일해'를 갖는다.

$Ax = b \quad \rightarrow \quad \begin{bmatrix}  4 & 1 & 3 \\  2 & 5 & 6  \end{bmatrix} \begin{bmatrix}  x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}  8 \\ -2 \end{bmatrix} \quad (m=2 < n=3)$

■ overdetermined인 경우 $m > n$, 해가 존재하지 않는 이유는  방정식의 개수가 미지수보다 많기 때문이다. 즉, $A$가 $m \times n$이기 때문이다.

■ 그러므로 가장 간단한 해결책은 $m \times n$을 $n \times n$으로 바꾸는 것이며, $n \times n$으로 만드는 간단한 방법은 $A^T$를 $A$에 곱하는 것이다. 

- $A^T$는 $n \times m$, $A$는 $m \times n$이므로 $A^T A$는 $n \times n$

■ $A^T A$는 $n \times n$이므로 정방행렬(또는 정사각행렬)이며 대칭행렬(symmetric matrix)이다.

- $A^T A)^T = A^T A^{TT} = AT A$가 성립하므로 $A^T A$는 대칭행렬이다. 

- 대칭행렬은 $A = A^T$를 만족하는 행렬이다. $A^T A$ 자체를 하나의 $A$로 본다면 $A = A^T$임을 알 수 있다.

■ 만약, $A^T A$가 full rank를 갖는다면 $A^T A$는 역행렬이 존재한다. 즉, 가역행렬이다.

- $A^T A$가 full rank를 가지려면, 원래 행렬 $A$의 모든 열들의 관계가 독립이면 된다.

■ 정리하면, $A^T A$는 정방행렬이자 대칭행렬이며, $A$의 모든 열들이 독립이면 $A^TA$는 역행렬이 존재한다.

■ $A \mathbf{x} = b, \quad (m > n)$은 $A$가 정방행렬이 아니므로 역행렬을 구할 수 없다. 즉, $\mathbf{x} = A^{-1}b$로 해를 구할 수 없다. 

■ 이 상황에서 근사해를 구하는 방법은 다음과 같이 $A^T$를 양변에 곱해주는 것이다.

$A^T A \hat{\mathbf{x}} = A^T b$

- 양변에 같은 행렬을 곱했으므로 식은 성립한다.

■ $A^T A \hat{\mathbf{x}} = A^T b$면, 이제 해는 근사해인 $\hat{x}$이며, $\hat{x}$가 의미하는 것은 최적해(optimal solution)이다. $\hat{x}$는 식을 만족시키는 해는 아니지만, $A$에 존재하는 모든 방정식을 최대한 만족시키는 해(solution)이다.

■ $A^T A$가 full rank라면, 역행렬이 존재하므로 다음과 같이 $A^T A$의 역행렬을 양변에 곱해주면 최종적인 해( 해가 존재하지 않는 $A \mathbf{x} = b$에 대한 최적해)를 구할 수 있다.

$A^T A \hat{\mathbf{x}} = A^T b$
$(A^T A)^{-1} A^T A \hat{\mathbf{x}} = (A^T A)^{-1} A^T b$
$\hat{\mathbf{x}} = (A^T A)^{-1} A^T b$

■ 이것이 왜 최소자승법과 관련이 있냐면, 예를 들어 다음과 같은 데이터가 있을 때, 데이터 포인트들과 가장 근사한 직선 $y = ax + b$의 $a, b$를 찾는다면

- 최소제곱은 '가장 가깝거나', '오차가 가장 적은 것'을 의미한다.

- 그러므로 최소제곱직선은 가장 가까운(근사한) 직선, 오차가 가정 적은 직선이라고 할 수 있다. 

- 이 예시에서 최소제곱직선 $y = ax + b$를 결정하기 위해 $a, b$를 찾는데, 이 $a$와 $b$를 '최소제곱해'라고 한다.

■ 주어진 정보 $(1, 1), (2, 3), (3, 4), (4, 3)$을 이용해 $a, b$를 찾아야 한다. $y = ax + b$에 $(1, 1), (2, 3), (3, 4), (4, 3)$을 대입하면 다음과 같은 선형연립방정식이 생긴다.

이를 행렬로 표현하면 다음과 같이 $A \mathbf{x} = b$의 형태가 되며, $A$의 크기는 $m > n$이 된다.

문제를 풀기 위해 양변에 $A^T$를 곱하면 다음과 같다.

정방행렬 $A^T A$의 행렬식 $\text{det} (A^T A) \neq 0$이므로 $A^T A$는 가역행렬이다. 그러므로 최적해는 다음과 같다.

■ 단, 이 예시에서 최적해를 구할 수 있었던 이유는 행렬 $A$의 모든 열이 독립이므로 $A^T A$의 역행렬이 존재할 수 있었다.

■ 즉, 행렬 $A$의 열들이 종속 관계를 갖는다면 최적해를 구할 수 없다.

■ 그러므로 overdetermined에서 최적해를 구할 수 있으려면 $A^T A$가 가역행렬이어야 하며, 이는 행렬 $A$의 모든 열이 독립. 즉, 행렬 $A$의 계수(rank)가 $n$과 같아야 한다. (= full rank여야 한다.)

■ 또한, $A$의 rank가 $n$이라면, $A^T A$의 rank도 $n$인 것을 알 수 있다. $\text{rank} A = \text{rank} A^T A = n$ 그러므로 $A^T A$의 영공간은 $A$의 영공간과 같다.

■ 정리하면, $m > n$인 $A$에 대해서 $A \mathbf{x} = b$의 해를 구하지 못할 때, 최적해를 구하기 위해 $A^T A \hat{\mathbf{x}} = A^T b$를 풀어야 하는데, 이를 풀기 위해서는

- $A^T A$가 반드시 가역행렬이어야 하며, 이는 $A^T A$가 full rank여야 함을 의미한다.

- $A^T A$가 full rank가 되려면, 원래 행렬 $A$의 열들이 선형 독립이어야 한다. 즉, $A$의 rank가 $n$이어야 한다. 

- 즉, $\text{rank} (A^TA) = \text{rank} (A)$가 되며, 퇴화차수 정리에 의해 두 행렬의 영공간이 같음을 알 수 있다. $N(A^T A) = N(A)$

- 이 예시에서는 rank는 2이고 전체 공간은 2차원이므로 퇴화차수 정리에 의해 영공간은 0차원이다. 즉, 이 예시에서 $A^T A$와 $A$의 영공간에는 영벡터만 존재함을 의미한다. $N(A^TA) = N(A) = \left\{ 0 \right\}$

 

2. 2D Vector Projection(2차원 벡터 투영)

■ 벡터 투영은 하나의 벡터를 다른 벡터에 투영(=사영)(projection)시키는 것을 의미한다. 

■ 벡터를 투영하는 이유는 다양하며, 그 중 하나로 '벡터를 다른 벡터(또는 직선, 평면 등)에 대해 평행 성분과 수직 성분으로 분해하기 위하여 사용하는 경우가 있다.

■ 예를 들어 다음과 같이 평행하지 않은 두 벡터가 존재한다고 했을 때

■ 벡터 $a$에서 벡터 $b$의 종점과 가장 가까운 지점을 찾는다. 그 지점은 다음과 같이 바로 벡터 $a$와 벡터 $b$의 종점이 수직인 지점이다.

■ 벡터 $a$와 벡터 $b$의 종점이 수직인 지점이 시점이고 $b$의 종점이 종점인 벡터를 $c$라고 했을 때, $b$를 서로 직교하는 벡터 $a$와 $c$의 벡터 합으로 분해할 수 있다. $b = a + c$

■ 이때, $b$를 $a$ 위로의 사영을 시킨 벡터를 정사영 벡터라고 하며, 이 정사영 벡터가 $a$ 방향으로 '평행'한 성분이다. 그리고 $a$에 수직인 성분은 $b$에서 평행 성분인 정사영 벡터를 뺀 나머지로, 벡터 $c$가 이에 해당된다.

■ 다시 돌아와서, 다음과 같이 $a$ 위에서 $b$에 가장 가까운 점을 $p$라고 할 때, 원점에서 $p$까지의 벡터를 $p$라고 하자. 벡터 $p$는 벡터 $b$를 벡터 $a$에 투영(사영)시킨 벡터이다.

■ 그리고 벡터 $a$에 수직인 성분 벡터를 $e$라고 하자. 이 $e$는 벡터 $b$와 투영시켰을 때의 벡터 $p$ 사이의 오차(error)를 의미한다.

- 여기서의 오차는 투영 전과 투영 후, 거리상으로 얼마나 차이나는지

■ 벡터 $e$는 투영 대상인 벡터 $a$와 직교(orthogonal)하며, $e = b - p$로 나타낼 수 있다. 이 식을 이항하여 $p$에 대한 식으로 나타내면 $p = b - e$가 된다. 즉, 벡터 $b$에서 오차 $e$만큼 뺀 것은 투영(사영) 벡터 $p$가 되는 것이다.

■ 위의 그림에서 벡터 $p$는 벡터 $a$와 평행 관계임을 알 수 있다. 즉, 벡터 $a$의 스칼라배가 벡터 $p$이고 벡터 $p$의 스칼라배가 벡터 $a$이다. 스케일 상수를 $x$라고 한다면 벡터 $p = x \cdot a$로 나타낼 수 있다.

■ 여기서 스케일 상수 $x$를 찾는 방법은, 벡터 $a$와 $e$가 수직 관계임을 이용하면 된다. 즉, 벡터 $a$와 $e$의 내적 결과가 0이라는 점과 벡터 $e$는 $e = b - p$로 나타낼 수 있음을 이용하면 된다. 그러면 다음 식이 성립한다.

$a^T (b-p) = a^T (b - xa) = 0$

- 여기서 $a$를 전치한 $a^T$는 행벡터, $e = b - xa$는 열벡터

■ $a^T (b-p) = a^T (b - xa) = 0$를 전개해서, 스케일 상수 $x$에 대한 식으로 정리하면 다음과 같다.

$a^T (b - x a) = 0$
$a^T b - x a^T a = 0$
$x a^T a = a^T b$

$x = \dfrac{a^T b}{a^T a}, \quad  p = ax = \dfrac{a^Tb}{a^Ta} a$

- 여기서 $\dfrac{a^Tb}{a^Ta}$는 내적이므로 결과 값은 상수이다. 

- 그러므로 $x$는 벡터 $a$에 곱해지는 스칼라가 된다. 

cf) 참고로 투영 벡터에 대한 식에는 코사인이 내장되어 있다. $a^T b = \| a\| \| b\| \cos(\theta)$

2.1 projection matrix

■ $p = a \dfrac{a^Tb}{a^Ta}$에서 벡터 $b$의 길이가 2배가 된다면, 벡터 $p$의 길이도 2배가 될 것이다. 

■ 만약, 벡터 $a$의 길이가 2배가 된다면, 투영 벡터의 식의 $a$를 $2a$라고 생각하면, 분자와 분모의 2는 모두 소거되어 원래의 식과 같아진다. 즉, 벡터 $a$는 아무리 늘리거나 줄여도 투영 벡터 $p$에는 영향을 미치지 않는다.

■ $p = a \dfrac{a^Tb}{a^Ta}$에서 $P = \dfrac{aa^T}{a^Ta}$라고 한다면, 투영 벡터 $p = Pb$로 나타낼 수 있으며, $P$는 분모가 벡터의 내적이므로 상수, 분자는 열벡터 $\times$ 행벡터 순으로 곱해져 있으므로 행렬로 볼 수 있다. 이런 $P$를 투영행려(projection matrix)라고 부른다. 

■ 그러므로 벡터 $b$는 투영행렬에 의해 벡터 $a$로 투영되며, 투영행렬이 바로 벡터 $b$를 벡터 $a$로 투영시키는 매개체라고 할 수 있다.

2.1.1 projection matrix == symmetric matrix

■ 어떤 행렬 $A$가 있을 때, $A$의 열벡터들의 선형 결합으로 만든 공간을 행렬 $A$의 열공간 $C(A)$라고 한다. 

■ 행렬 $A$에 임의의 벡터 $\mathbf{x}$를 곱한 결과도 행렬 $A$의 열공간에 존재하는데, 이는 다음과 같이 행렬과 임의의 벡터를 곱하는 $A \mathbf{x}$도 열벡터들의 선형 결합이기 때문이다.

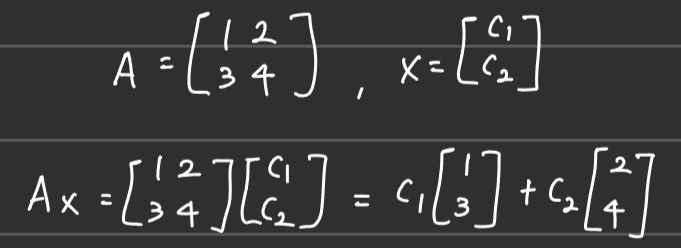
■ $p = Pb$도 마찬가지로 행렬 $P$에 벡터 $b$가 곱해진 형태이다. 즉, $Pb$도 $P$의 열공간에 존재한다. 

■ 그리고 투영행렬 $P$의 열공간은 벡터 $a$를 지나가는 직선이 된다. 그 이유는 투영행렬 $P$는 $aa^T$로. 즉, 열벡터 $\times$ 행벡터의 순서로 곱해졌기 때문에 rank = 1인 행렬이다.

■ 열공간의 차원은 1이며, $aa^T$이므로 그 위에 벡터 $a$가 있는 것으로 볼 수 있다. 즉, 벡터 $a$는 투영행렬 $P$의 열공간의 기저라고 할 수 있다.

■ 그리고 투영행렬 $P$는 벡터 $a$의 열벡터 $\times$ 행벡터 순으로 곱하여 만들어진 행렬이므로 대칭행렬이다. $P^T = P$

■ 만약, 투영을 두 번하면 어떻게 될까(= $p = P^2b$인 상황) 결과는 동일하다.(투영 벡터 $p$는 변하지 않는다.)

- 다음과 같은 그림으로 이해하면 될 것 같다.

- $b$를 $a$ 위로의 사영시키면 벡터 $p$가 만들어질 것이다. 

- 여기서 투영을 추가로 한다고 해도 투영 벡터 $p$가 변하지 않는다. 추가로 투영해도 결국, 투영 벡터 $p$를 변화시킬 수 있는 $b$가 바뀌지 않았으니 달라지는 것은 없다.

- 즉, 두 번 투영해도 첫 번째 투영에서 얻은 것과 같은 투영 벡터를 얻는다.

■ 이를 통해 할 수 있는 것은 $P^2 = P$이다. 

■ 정리하면, 투영행렬 $P$는 대칭행렬($P^T = P$)이며 rank = 1인 행렬이다. 그리고 $P$의 제곱은 $P$와 같으며 $P$의 영공간은 벡터 $a$를 지나가는 직선이다. 

 

3. N - Dimensional Vector Projection(N차원 벡터 투영)

■ 투영을 하는 이유는 해가 없는 $A \mathbf{x} = b$를 다루기 위해서이다.

■ $A \mathbf{x}$는 $A$의 열벡터들의 선형 결합으로 볼 수 있으므로 $A \mathbf{x}$는 항상 $A$의 열공간에 있을 것이다. 

■ 그렇다면, $A \mathbf{x} = b$가 성립하기 위해서는 $b$도 $A$의 열공간에 존재해야 한다.

■ 해가 없는 경우는 우변 $b$는 $A$의 열공간에 존재하지 않기 때문에 발생한다. 그래서 투영을 통해 $b$를 행렬 $A$의 열공간에서 가장 가까운(=근사한) 벡터로 바꾸는 것이다.

■ 가장 가까운 벡터를 $p$라고 했을 때, 해가 없는 경우 $A \hat{\mathbf{x}} = p$를 풀면 된다.

- $p$는 $b$를 $A$의 열공간으로 투영한 벡터이다. 

- $\hat{\mathbf{x}}$는 $\mathbf{x}$가 아닌, 가능한 최선의 $\mathbf{x}$이다.

■ 예를 들어 3차원 공간에 평면이 있고, 평면에 없는 벡터 $b$가 있다고 했을 때, $b$를 평면에 투영하자.

■ 투영하는 방법은 2D vector projection과 동일하게 벡터 $b$와 가장 가까운 점을 평면에서 찾으면 된다. 즉, 수직이 되는 지점을 찾으면 된다.

■ 여기서 점 $p$는 평면 위의 점이므로 평면이 무엇인지 알아야 한다.

■ 그리고 2차원 평면을 알기 위해서는 2차원 평면을 생성하는 두 기저를 확인하면 된다. 

■ 만약 2차원 평면을 생성하는 기저를 $a_1, a_2$라고 하면, 기저는 서로 독립이므로 다음과 같이 다른 방향을 바라볼 것이다.  

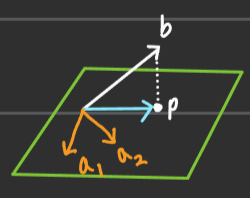
■ 이 평면은 행렬 $A$의 열공간이라고 했을 때, 기저가 $a_1, a_2$이므로 행렬 $A$를 $A =  \begin{bmatrix} | & | \\ a_{1} & a_{2} \\ | & | \end{bmatrix}$로 나타낼 수 있다.

■ 벡터 $b$는 $A \mathbf{x} = b$의 우변 $b$이다. 벡터 $b$는 평면 위에 존재하지 않는 벡터로 가정했기 때문에 $b$는 $A$의 열공간인 평면 위에 존재하지 않는다.

■ 즉,  $A \mathbf{x} = b$를 만족하는 $\mathbf{x}$가 존재하지 않는 상황이다. 그래서 최대한 만족시키는 해를 찾기 위해 위의 그림과 같이 $A$의 열공간에 투영하여 $A$의 열공간인 2차원 평면 위에 있는 벡터들 중에 $b$와 가장 근접한 벡터를 찾는 것이다.

■ 벡터 $b$와 오차가 가장 적은. 즉, $b$와 가장 근접한 벡터는 위의 그림과 같이 오차 벡터(실선)와 수직 관계를 갖는 벡터 $p$이다.

■ 벡터 $p$와 가장 근사한 $p$는 평면에 포함된 벡터이므로, $p$는 $A$의 열벡터들의 선형 결합으로 만들 수 있는 벡터인데, 선형 결합의 형태가 $A \hat{\mathbf{x}}$이므로 $p = A \hat{\mathbf{x}}$으로 나타낼 수 있다. 

- 이 예시에서 벡터 $p$는 다음과 같은 선형 결합으로 나타낼 수 있다. $p = \hat{\mathbf{x}} a_1 + \hat{\mathbf{x}} a_2$

■ $p = A \hat{\mathbf{x}}$에서 찾고자 하는 것은 $\hat{\mathbf{x}}$이며, $\hat{\mathbf{x}}$는 오차를 의미하는 벡터 $e$를 이용해서 구할 수 있다.

■ 벡터 $e$는 평면과 수직이므로 벡터 $e$와 평면 위의 모든 벡터의 내적은 0이 된다. 이때, $e = b - p$이며 $p = A \hat{\mathbf{x}}$이므로 $b - A \hat{\mathbf{x}}$와 평면 위의 모든 벡터의 내적은 0이라고 할 수 있다.

■ 이 예시에서 평면 위의 벡터는 2차원 평면을 만드는 기저 $a_1, a_2$이므로, 다음과 같은 식이 성립한다.

$\mathbf{a}_{1}^T\bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0,  \quad  \mathbf{a}_{2}^T\bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0$

■ 내적은 행렬 안에서 발생하는 연산이다. 그러므로 위의 두 내적을 행렬의 형태로 다음과 같이 나타낼 수 있다.

$\begin{pmatrix} a_1^T \\ a_2^T \end{pmatrix} \bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$
$A^T \bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0$
$A^T A\,\hat{\mathbf{x}} = A^T \mathbf{b}$

■ 여기서 $\begin{pmatrix} a_1^T \\ a_2^T \end{pmatrix} \bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$
$A^T \bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0$의 형태를 보면 left nullspace의 형태인 것을 볼 수 있다. 즉, 오차 벡터 $e = b - A \hat{\mathbf{x}}$는 left nullspace에 존재한다. 

■ left nullspace는 행렬 $A$의 열공간과 직교한다. 위의 그림에서 행렬 $A$의 열공간이 평면, 실선이 벡터 $e$이다.  

3.1 solution of $\hat{\mathbf{x}}$ and projection matrix

■ $A^T \bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0$으로 다음과 같이 근사해를 구할 수 있다. 

$\hat{\mathbf{x}} = (A^T A)^{-1} A^T \mathbf{b}$

■ 이대 $\hat{\mathbf{x}}$의 왼쪽에 행렬 $A$를 곱하면 $A \hat{\mathbf{x}} = p$가 된다. 위의 식에서 양변에 행렬 $A$를 왼쪽에 곱하면, 다음 식이 성립한다.

$p = A \hat{\mathbf{x}} = A (A^T A)^{-1} A^T b$

■ 즉, 원래 벡터 $b$를 $A$의 열공간으로 투영한 벡터 $p$는 $p = (A^T A)^{-1} A^T \mathbf{b}$이다.

■ 여기서 $p = Pb$이므로 투영 행렬 $P$에 대한 식은 $P = A (A^T A)^{-1} A^T$가 된다.

■ 이 투영 행렬 $P = A (A^T A)^{-1} A^T$가 어떠한 벡터도 행렬 $A$의 영공간으로 투영시킬 수 있는 투영 행렬이 된다.

- $P = A (A^T A)^{-1} A^T$는 $n$차원에서 투영 행렬을 구하는 방법이다.

- 그리고 $n$차원에서도 $P^T = P$, $P^2 = P$가 성립한다.

- $P^T  = \bigl(A(A^T A)^{-1} A^T\bigr)^T = A^{TT}\bigl(A^T A^{TT}\bigr)^{-1} A^T = A\,(A^T A)^{-1} A^T = P$

-- \( (A^T)^{-1} = (A^{-1})^T \)

- $P^2  = A\,(A^T A)^{-1} A^T \,A\,(A^T A)^{-1} A^T = A\,(A^T A)^{-1} A^T = P$

■ 만약, 행렬 $A$가 정방행렬이고 역행렬이 존재한다면, $P = A (A^T A)^{-1} A^T$는 $P = A\,A^{-1}\,(A^T)^{-1} A^T = I$로 단위행렬이 된다.

- 투영 행렬이 단위 행렬이 되므로 투영을 시켰을 때, 어떠한 변화도 발생하지 않게 된다.