Matrix spaces; rank 1

1. 행렬 공간(Matrix spaces)

■ 행렬 공간은 모든 $3 \times 3$ 크기의 (정방)행렬의 공간을 의미한다.

■ 행렬 공간은 벡터 공간에 대한 조건을 만족하므로 행렬 공간은 벡터 공간이다. 그 이유는 행렬들끼리 선형 결합을 한 결과도 같은 차원의 공간에 위치하기 때문이다.

■ 예를 들어 다음과 같은 $3 \times 3$행렬 $M_1, M_2$와 임의의 상수 $c_1, c_2$가 존재할 때, $M_1$과 $M_2$의 선형 결합은 다음과 같다.

$c_1 M_1 + c_2 M_2 = c_1  \begin{bmatrix}  a_{11} & a_{12} & a_{13} \\  a_{21} & a_{22} & a_{23} \\  a_{31} & a_{32} & a_{33}  \end{bmatrix}  + c_2  \begin{bmatrix}  b_{11} & b_{12} & b_{13} \\  b_{21} & b_{22} & b_{23} \\  b_{31} & b_{32} & b_{33}  \end{bmatrix}$

■ 위와 같이 선형 결합을 해도 선형 결합 결과 행렬은 여전히 같은 차원의 행렬 공간에 존재한다. 둘을 더한 행렬은 덧셈을 했을 때 결과가 집합 내부에 머무는가 $u + v \in V$를 만족한다. 그리고 $c_1 M_1$이나 $c_2 M_2$는 $c \cdot u \in V$를 만족한다. 

■ 그러므로 $M_1, M_2 \in V$라면 두 행렬의 선형 결합 $c_1 M_1 + c_2 M_2$도 $c_1 M_1 + c_2 M_2 \in V$가 된다.

■ 이렇게 되는 이유는, 선형 결합 연산은 역 연산이 가능하기 때문이다. 여기서의 선형 결합은 임의의 상수를 곱하고 같은 공간 $V$에 있는 어떤 행렬과 다른 행렬에 대해 덧셈 연산을 한 것이므로, 반대로 뺄셈 연산을 수행하고 곱한 상수만큼 나누면 $V$에 속하는 원래의 행렬로 돌아온다. 그러므로 행렬들끼리 선형 결합을 한 결과가 같은 차원의 공간에 위치하는 것은 당연한 결과이다.

■ 반면, 행렬곱 $M_1 M_2$는 공간이 달라진다. $M_1 M_2$는 다음과 같이 선형 결합 연산과는 다른 형태 또는 성질을 가지기 때문에 '공간 안에서 선형 결합'으로 보지 않는다.

$M_1 M_2 = \begin{bmatrix}  a_{11} & a_{12} & a_{13} \\  a_{21} & a_{22} & a_{23} \\  a_{31} & a_{32} & a_{33}  \end{bmatrix}  \begin{bmatrix}  b_{11} & b_{12} & b_{13} \\  b_{21} & b_{22} & b_{23} \\  b_{31} & b_{32} & b_{33}  \end{bmatrix}$

- 예를 들어 두 개의 $3 \times 3$ 대칭행렬을 더하면(혹은 빼면) 여전히 대칭행렬이다. 하지만 두 대칭행렬을 행렬곱하면 더 이상 대칭행렬이 아닐 수 있다.

1.1 행렬 공간의 기저, 차원

■ $3 \times 3$ 크기의 행렬 $M$은 부분공간을 가지며, $M$의 부분 공간으로 다음과 같은 행렬들을 가질 수 있다.

- ① $3 \times 3$ 대칭행렬

- ② $3 \times 3$ 상삼각행렬

- ③ $3 \times 3$ 대각행렬

■ 여기서 알고 싶은 것은 위의 부분공간 행렬들의 기저와 차원이다.

1.1.1 Basis of M

■ 기저 벡터가 되기 위해서는 기저 벡터들은 선형 독립이어야 하며, 기저 벡터들의 선형 결합을 통해 기저 벡터가 속하는 공간 내에 있는 어떠한 벡터도 생성할 수 있어야 한다. 

■ 그리고 차원은 행렬의 rank와 같으며, rank는 행렬 안의 벡터들이 정의할 수 있는 차원을 의미한다. 즉, $3 \times 3$ 행렬의 rank = 3이라면, 행렬의 행벡터나 열벡터들의 선형 결합으로 표현할 수 있는 공간의 차원을 의미한다.

■ 그러나 행렬 공간의 차원은 조금 다르다. 여기서는 $3 \times 3$ 크기의 행렬 $M$을 하나의 벡터로 간주하고, 그 행렬이 표현할 수 있는 공간이다. 

■ 벡터의 차원은 벡터를 구성하고 있는 성분의 수이다.

■ 그러므로  행렬 $M$을 하나의 벡터로 간주할 경우, 행렬 공간의 차원은 행렬 $M$을 구성하고 있는 원소의 개수가 된다. $M$은 $3 \times 3$이므로 $M$의 차원은 9가 된다.

■ $M$의 차원은 9차원. 즉, $M$은 9차원 공간이므로 $M$의 기저는 9개이며, 여기서는 행렬을 하나의 벡터로 간주하므로 $M$의 가장 간단한 기저는 다음과 같다.

$$\overset{M_1}{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_2}{\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_3}{\begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_4}{\begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_5}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_6}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix}} \overset{M_7}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}} \overset{M_8}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}} \overset{M_9}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}}$$ - 기저가 1과 0으로 구성되어 있기 때문에 위의 9가지 기저 행렬은 표준 기저이다.

■ 위의 9가지 기저 행렬의 선형 결합을 통해  $3 \times 3$ 크기 행렬을 어떠한 형태라도 만들 수 있다.

■ 즉 $3 \times 3$ 크기 $M$의 부분 공간인 ① $3 \times 3$ 대칭행렬, ② $3 \times 3$ 상삼각행렬, ③ $3 \times 3$ 대각행렬은 위의 9가지 기저 행렬의 선형 결합으로 만들 수 있으며, 선형 결합의 결과는 여전히 $M$과 동일한 공간에 존재하기 때문에 $3 \times 3$ 크기의 대칭행렬, 상삼각행렬, 대각행렬은 $M$의 부분공간이 되는 것이다.

1.2 Symmetric matrix as a subspace of M

■ 다음과 같은 $3 \times 3$ 대칭행렬을 $S$라고 하자. $S$는 $M$의 부분공간이며, 주대각선을 기준으로 위아래의 원소들이 대칭 형태이다.

$S = \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix}$

■ 행렬 $M$의 9가지 기저행렬 중 $M_1, M_5, M_9$는 대칭행렬이므로 $M$의 기저행렬 $M_1, M_5, M_9$는 $S$의 기저에 포함된다.

■ 그리고 $M_2$와 $M_4$의 선형 결합 $1 \cdot M_2 + 1 \cdot M_4$, $M_3$와 $M_7$의 선형 결합 $1 \cdot M_3 + 1 \cdot M_7$, $M_6$와 $M_8$의 선형 결합 $1 \cdot M_6 + 1 \cdot M_8$으로 대칭행렬을 만들 수 있다. 그러므로 이들의 선형 결합의 결과도 대칭행렬의 기저에 포함된다.

■ 대칭행렬 $S$의 기저는 위의 기저들을 포함하여 다음과 같이 6개가 된다.

$\underset{S_1}{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{S_2}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{S_3}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}} \underset{S_4}{\begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{S_5}{\begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix}} \underset{S_6}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix}}$

■ 기저가 6개라는 것은 대칭행렬 $S$의 차원은 6차원이라는 의미이다. 이 6가지 대칭행렬의 기저의 선형 결합을 통해 대칭행렬 공간에 존재하는 어떠한 행렬도 만들 수 있다.

1.3 Upper triangular matrix as a subspace of M

■ 다음과 같은 $3 \times 3$ 상삼각행렬을 $U$라고 하자. $U$역시 $M$의 부분공간이며, 다음과 같은 형태를 갖는다.

$U = \begin{bmatrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{bmatrix}$

■ 행렬 $M$의 9가지 기저행렬 중 $M_1, M_2, M_3, M_5, M_6, M_9$는 상삼각행렬이므로 $M$의 기저행렬 $M_1, M_2, M_3, M_5, M_6, M_9$는 $U$의 기저에 포함된다.

■ 상삼각행렬 $U$는 위의 기저들을 기저로 가진다.

$\underset{U_1}{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{U_2}{\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{U_3}{\begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{U_4}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}} \underset{U_5}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix}} \underset{U_6}{\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}}$

■ 상삼각행렬도 6개의 기저를 가지므로 상삼각행렬 $U$의 차원은 6이다. 그리고 이 6가지 상삼각행렬의 기저의 선형 결합을 통해 상삼각행렬 공간에 존재하는 어떠한 행렬도 만들 수 있다.

1.4 Diagonal matrix as a subspace of M

■ 대각행렬을 $D$라고 하자. 대각행렬 $D$는 다음과 같이 $M$의 부분공간 대칭행렬 $S$와 상삼각행렬 $U$의 교집합으로 정의할 수 있다.

$S \cap U = D \quad \Rightarrow \quad \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix} \cap \begin{bmatrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{bmatrix} = \begin{bmatrix} a & 0 & 0 \\ 0 & d & 0 \\ 0 & 0 & f \end{bmatrix}$

- 대각행렬 $D$의 원소 $a, d, f$는 모두 $S$와 $U$에 있는 벡터들이다.

■ 대각행렬 $D$는 3개의 원소만 있기 때문에 $D$의 차원은 3차원이다. 즉, $\text{dim} (S \cap U) = \text{dim} (D) 3$으로 표현할 수 있다.

■ 반면, $S$와 $U$의 합집합. 즉, $S$에 있거나 $U$에 있는 원소들로 정의되는 합집합 $S \cup U$는 $S \cap U$와 달리 $M$의 부분공간으로 성립되지 않는다.

$S \cup U = D \quad \Rightarrow \quad \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix} \cup \begin{bmatrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{bmatrix}$

■ $S \cup U$을 $M$의 두 부분공간이 합쳐지는 것으로 생각할 수 있는데, 이것은 애초에 성립되지 않는다.

- $S$와 $U$는 9차원 공간 $M$의 6차원 부분공간이다. 이 둘의 기저 행렬들을 기저 벡터로 생각한다면, 기저 행렬은 서로 다른 방향을 향하고 있기 때문에, 단순히 $S$와 $U$를 합칠 수 없다.

■ 단, $S$와 $U$의 합은 성립한다. 그 이유는 다음과 같이 $S$와 $U$를 더하면, $M$ 형태의 행렬이 되기 때문이다. 정확히는 두 부분공간을 더해서 만들어지는 행렬은 9개의 원소를 가지므로 9차원 공간인 $M$이 된다.

$S + U = M \quad \Rightarrow \quad \begin{bmatrix} a & b & c \\ b & d & e \\ c & e & f \end{bmatrix} + \begin{bmatrix} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{bmatrix} = \begin{bmatrix} a' & b' & c' \\ d' & e' & f' \\ g' & h' & i' \end{bmatrix}$

■ 즉, $S + U$는 $S + U$ = any element of $S$ + any element of $U$ = all 3 \times 3 Matrix가 된다. $S$와 $U$의 선형 결합을 통해 어떠한 $3 \times 3$행렬 $M$을 만들어 낼 수 있다는 것이다.

■ $3 \times 3$ 크기의 행렬 $M$에 대한 부분공간의 차원을 정리하면 다음과 같다.

- $\text{dim} (M) = 9$이고 

- ① $\text{dim} (S) = 6$

- ② $\text{dim} (U) = 6$

- ③ $\text{dim} (S \cap U) = 3$

- ④ $\text{dim} (S + U) = 9$

■ 여기서 $\text{dim} (S) = 6$ + $\text{dim} (U) = 6$ = 12이며 $\text{dim} (S \cap U) = 3$ + $\text{dim} (S + U) = 9$ = 12가 되는 것을 볼 수 있다.

■ 즉, 두 부분공간이 있다면, 두 부분공간의 차원을 더한 것은 두 부분공간의 교집합의 차원과 합의 차원을 더한 것과 같다.

\( \text{dim}(S) + \text{dim}(U) = \text{dim}(S \cap U) + \text{dim}(S + U) \)

 

2. 선형대수와 미분 방정식(differential equation)의 관계

■ 벡터 공간이지만, 벡터가 없는 벡터 공간이 있다. 이것은 미분 방정식에서 나온다.

■ 예를 들어 다음과 같은 미분 방정식이 있다고 가정해 보자. $$\dfrac{d^2 y}{dx^2} + y = 0$$ ■ 이 미분 방정식의 해는 다음과 같은 것들이 가능하다.

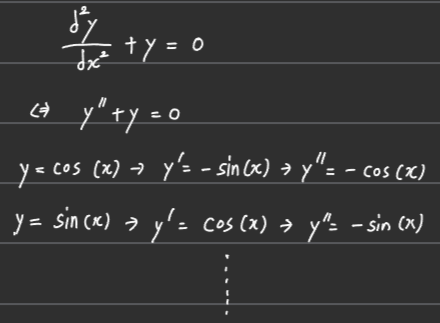
■ 이 예시에서 미분 방정식의 해는 다양하겠지만, $sin(x), cos(x)$ 2가지만 존재한다고 가정하면, $sin(x), cos(x)$는 미분 방정식의 영공간을 나타내는 것으로 볼 수 있다.

■ 그렇다면, 미분 방정식의 영공간의 완전해(complete soultion)은 다음과 같이 $sin(x), cos(x)$의 선형 결합으로 정의할 수 있다.

$y = c_1 \cos(x) + c_2 \sin(x)$

■ 이렇게 선형 결합으로 표현할 수 있기 때문에 \(
y = c_1 \cos(x) + c_2 \sin(x)
\)를 벡터 공간이라고 할 수 있으며, 이 공간의 기저는 $sin(x), cos(x)$가 된다.

■ 기저가 2개이므로 이 미분 방정식의 차원(정확히는 해공간의 차원)은 2차원이다. 이는 사실 미분 방정식이 2계이기 때문이다. 

■ 정리하면, 선형 미분 방정식의 해를 구한다는 것은 방정식의 해공간에 대한 기저를 찾는 것이다. 

■ 예시와 같은 선형 미분 방정식은 벡터처럼 보이지 않고 함수처럼 보인다. 하지만, 이런 선형 미분 방정식을 벡터라고 부를 수 있다. 왜냐하면 더할 수 있고 상수로 곱할 수 있으므로 선형 결합을 취할 수 있기 때문이다. 

 

3. Rank 1 matrices

■ 예를 들어 다음과 같이 계수(rank)가 1인 행렬 $A$이 있다고 할 때

$A = \begin{bmatrix} 1 & 4 & 5 \\ 2 & 8 & 10 \end{bmatrix}$

■ row1은 row2의 두 배이므로 row1과 row2는 종속 관계를 갖는다. 즉, row1과 row2는 같은 선상에 위치한다.

■ col1, col2, col3도 실수배 관계에 있기 때문에 종속 관계를 갖으며, col2와 col3는 col1과 같은 선상에 위치한다.

■ 그러므로 이 행렬의 행공간의 기저 개수는 1개이며 열공간의 기저 개수도 1개이다. 즉, 행공간과 열공간은 모두 1차원이다. \( \text{dim} (C(A)) = \text{dim} (C(A^T)) = rank (A) \) 

■ 정리하면, rank = 1인 행렬이 표현할 수 있는 공간은 1차원 직선이다.

■ 열공간의 기저(=열벡터)를 $[1 2]^T$ $u$, 행공간의 기저(=행벡터)를 $[1 4 5]^T$, $v$라고 했을 때

- 행공간의 기저는 $C(A^T)$의 기저이므로 열벡터

■ 여기서 어떤 열벡터와 어떤 행벡터를 column, row 순으로 곱하면 rank 1 행렬 $A$가 다음과 같이 만들어지는 것을 확인할 수 있다. $A = uv^T$

■ 예를 들어 $5 \times 14$크기의 행렬이 있고, 이 행렬의 rank = 4라고 하자. 그러면 다음과 같이 rank = 1 행렬 4개의 조합으로 이를 표현할 수 있다. 

- $A$는 rank = 4인 $5 \times 14$ 크기의 행렬. $B, C, D, E$는 rank = 1인 $5 \times 14$ 크기의 행렬

- 이렇게 원래 행렬을 rank 1 행렬들로 분해하여 나타낼 수 있다.

3.1 rank 1 행렬의 부분공간

■ 예를 들어 $5 \times 14$ 크기의 모든 행렬을 $M$이라고 가정해보자. $M = \textit{all } 5 \times 14 \textit{ matrices}$

■ 집합 $M$ 중에서 rank = 4인 행렬들은 $M$의 부분 공간이 될 수 있을까. 부분 공간이 되려면 영벡터를 포함하고 스칼라곱을 한 결과와 행렬 끼리의 덧셈 연산에 대해 닫혀 있어야 하지만, 이 조건을 만족하지 않는다.

■ 즉, rank = 4인 어떤 행렬과 rank = 4인 또 다른 행렬의 선형 결합 연산을 수행한 결과가 같은 공간에 존재하지 않을 수 있다. ■ 예를 들어 다음과 같이 rank = 2인 행렬 $A$와 $B$가 있을 때 $A + B$의 rank는 3이 된다.

즉, 같은 rank를 가지는 서로 다른 행렬의 선형 결합 결과가 rank = 3이 되어 원래의 rank = 2의 차원에서 벗어나게 된다. 

3.1.1 $\mathbb{R}^4$ case

■ 이번에는 4차원 공간인 $\mathbb{R}^4$의 공간에서, $\mathbb{R}^4$의 공간상의 모든 벡터는 다음과 같이 4개의 성분을 가지는 벡터로 표현된다.

$\mathbf{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \\ v_4 \end{bmatrix}$

■ 이때 $\mathbb{R}^4$의 부분공간 $S$를 다음과 같이 정의하자.

$S = \textit{all } \mathbf{v} \textit{ in } \mathbb{R}^4 \textit{ with } v_1 + v_2 + v_3 + v_4 = 0$

■ $S$는 $\mathbb{R}^4$의 부분공간이며, 3차원이다.

- $S$는 하나의 선형 방정식 $v_1 + v_2 + v_3 + v_4 = 0$으로 정의되는 부분공간이다.

- 위 조건을 만족하는 모든 벡터는 $v_1 = -v_2 - v_3 - v_4$와 같이 표현되므로, $v_1$은 $v_2, v_3, v_4$에 따라 $v_1$이 결정된다. 

- $v_1 = -s - t - u$라고 하면, $v = [v_1, v_2, v_3,  v_4]$는

- $\mathbf{v} = (-s - t - u, s, t, u) = s(-1,1,0,0) + t(-1,0,1,0) + u(-1,0,0,1)$

- 이때 $[-1 1 0 0], [-1 0 1 0], [-1, 0, 0, 1]$은 서로 독립인 벡터 셋이고, 이들이 부분공간 $S$를 생성하므로 $S$의 차원은 3이 된다.

■ 사실 $v_1 + v_2 + v_3 + v_4 = 0$이므로 $[v_1, v_2, v_3, v_4]$는 어떤 행렬 $A$의 해. 즉, 영공간에 존재하는 벡터이다. 

■ 그러므로 $v_1 + v_2 + v_3 + v_4 = 0$을 만족하는 집합 $v$는 영공간이기 때문에, 벡터 $v$에 어떤 상수를 곱해도 0이 되고 같은 공간에 존재하는 다른 벡터와 선형 결합을 한 결과도 같은 공간에 존재하기 때문에 $S$는 $\mathbb{R}^4$의 부분공간이다. 

■ $v_1 + v_2 + v_3 + v_4 = 0$는 $A = [ 1 1 1 1 ]$라고 하면, $A \mathbf{v} = 0$으로 나타낼 수 있다.

■ $A = [ 1 1 1 1 ]$이므로 $A$의 rank = 1이다. 

- 영공간의 차원은 $n - r$이므로 $4 - 1 = 3$

■ $A$의 rank = 1이므로 pivot column의 개수는 1개. 즉, pivot variable은 1개이므로 free variable이 3개이다. 그러므로 free variable들을 하나씩 1, 0으로 설정하면,

■ $S$의 기저는 위에서 구한 것과 같이 $[-1 1 0 0], [-1 0 1 0], [-1, 0, 0, 1]$이다.

■ $A$의 열공간은 [1], [1], [1], [1]의 선형 결합으로 정의되며, 어떤 상수를 곱하고 더해도 결과는 상수값이 된다. 그러므로 $A$의 열공간은 $\mathbb{R}^1$이라고 할 수 있다.

■ $A$의 left nullspace $N(A^T)$는 $A^T \mathbf{x} = 0$을 찾으면 된다. 이때 $A^T$는 $[1 1 1 1 1]^T$이기 때문에 가능한 $mathbf{x}$는 0밖에 없다. 그러므로 $N(A^T) = \left\{0 \right\}$. 즉, $N(A^T)$의 차원은 0차원이다.

■ $mathbb{R}^4$에서 rank 1 행렬인 $A$의 주요 부분공간들의 차원을 보면, 

- 행공간의 차원은 rank인 1이고 영공간의 차원은 $n - r$이므로 3이된다. 두 부분공간의 차원의 합은 $\text{dim} (C(A^T)) + \text{dim} (N(A)) = 4$이며

- 열공간과 left nullspace의 차원의 합은 1 + 0 = 1이된다.

■ 이렇게 부분공간의 각 차원들은 원래 행렬 $A$의 차원을 나타낸다. 

- $A$는 $m \times n$행렬이며 $m = 1, n = 4$이며 

- 이는 $\text{dim} (C(A)) + \text{dim} (N(A^T)) = 1 + 0 = 1 \times 4 = \text{dim} (C(A^T)) + \text{dim} (N(A))$으로 표현할 수 있다.