1. Four fundamental subspaces
1.1 row space
■ 행공간에는 행벡터의 모든 선형 결합 결과가 담겨 있다. 즉, 행벡터가 행공간을 생성한다. 그렇다고 해서 행벡터들이 모두 행공간의 기저는 아니다. 정확히는 기저일 수도 있고, 아닐 수도 있다.
■ 행들이 독립적이라면 행공간의 기저가 되지만, 종속적일 때는 기저가 될 수 없다.
■ 그리고 행렬에는 '전치'가 있기 때문에 행렬을 회전하면, 행에서 열로 관점을 바꿀 수 있다. 즉 A의 행벡터들이 AT의 열벡터가 되는 것이다.
■ 그러므로 행공간을 AT의 열벡터들의 모든 선형 결합 결과가 담겨 있다고 할 수 있다. 즉 A의 행벡터들이 생성하는 공간과 AT의 열벡터들이 생성하는 공간은 동일한 공간이다.
row space=All combinations of rows of A=All combinations of columns of AT=C(AT)
1.2 left null space
■ left null space는 행렬 A 전치(AT)의 영공간이다.
left null space=null space ofAT=N(AT)
■ A가 m×n이라면, A의 영공간에는 n개의 성분을 가진 벡터들, Ax=0의 해가 존재한다. 즉, A의 영공간은 Rn에 있다.
■ 그리고 A의 열공간은 Rm에 있다. 왜냐하면 A가 m×n이면, 열벡터는 m개의 성분을 가지고 있기 때문이다.
■ AT의 열공간은 n×m이므로 Rn의 부분공간이다.
■ N(AT)도 A의 전치에 대한 영공간이므로 C(AT)가 Rm, C(AT)가 Rn인 것처럼, N(A)가 Rn의 부분공간이므로 N(AT)는 Rm의 부분공간이다.
■ 정리하면, 행렬 A가 m×n인 경우에 four fundamental subspaces는
- ① 행공간(row space)은 C(AT)이며, C(AT)는 Rn의 부분공간이다.
- ② 열공간(row space)은 C(A)이며, C(A)는 Rm의 부분공간이다.
- ③ 영공간(nullspace)은 N(A)이며, N(A)는 Rn의 부분공간이다.
- ④ left nullspace는 N(AT)이며, N(AT)는 Rm의 부분공간이다.
■ 정리한 기본적인 부분공간들을 그림으로 나타내면 다음과 같다.

- 열공간 C(A)의 차원은 계수(rank) r이다. dimC(A)=rank(A)=r
-- C(A)의 차원이 r인 이유는 rank는 pivot column의 수이므로 r개의 독립적인 열벡터가 열공간을 생성하기 때문이다.
- 동일한 이유로 행공간 C(A)T의 차원도 r이다.
- 이를 통해 알 수 있는 것은 행공간과 열공간은 같은 차원을 가진다는 것이다. dimC(A)=dimC(AT)=r
- 영공간을 구하기 위해서 행렬 A를 행사다리꼴행렬로 만들고 다시 기약행사다리꼴행렬로 만들어서 특수해(special solution)을 구하였다.
- 그리고 모든 특수해는 free variable에서 나왔다. 이 특수해들은 영공간에 있으며, 영공간의 기저가 되었다.
- m×n행렬에서 free variable의 수는 n−r개이므로 영공간에는 n−r개의 기저가 있는 것이다.
- 즉, 영공간의 차원 dimN(A)=n−r이다.
- left nullspace는 A의 전치이므로 n×m이다. 그러므로 N(AT)의 공간은 동일한 이유로 m−r이 된다. dimN(AT)=n−r
■ 그리고 위의 big picture를 보면, 행공간 C(AT)와 영공간 N(A)가 직교(orthogonal)하고, 열공간 C(A)와 N(AT)가 직교하는 것을 확인할 수 있다.
■ 이렇게 공간과 공간이 직교한다는 것은 각 공간 안에 있는 벡터들끼리 내적했을 때, 내적값이 0이 된다는 의미를 내포하고 있다. 예를 들어 다음과 같은 행렬 A가 있을 때 영공간에 있는 벡터를 하나 구해보면,

■ 이 예에서 A의 행공간을 생성하는 A의 기저는 [1 2 3]과 [4 5 6]이다.
■ 행공간 C(AT)와 영공간 N(A)가 직교하는지 확인하려면 영공간에 있는 벡터가 행공간에 있는 벡터 [1 2 3]과 [4 5 6]에 동시에 수직하는지 확인하면 된다.

■ 이 예시에서 행공간의 기저는 2개이므로 생성되는 행공간은 2차원 평면일 것이고, 열공간의 기저는 c를 스칼라라고 할 때, c⋅[−12−1]T이므로 열공간의 기저들이 생성하는 열공간은 하나의 직선이 된다. 그러므로 이 예시에서는 행공간의 기저가 만드는 평면에 열공간(직선)이 수직 관계를 갖지는 상황으로 이해할 수 있다.
■ 예를 들어 다음과 같이 m×n인 행렬 A를 기약행사다리꼴행렬 R로 만들었을 때, C(A)≠C(R)이다.

■ A에서 R을 만들기 위해 기본행연산을 수행하였다. 기본행연산 결과, 행공간을 만드는 행벡터는 A와 R모두 첫 번째 행과 두 번째 행임을 알 수 있다. 왜냐하면 기본행연산은 단순히 어떤 행의 실수배를 다른 행에 덧셈/뺄셈 연산을 수행하는 것이기 때문이다.
■ 즉, 기본행연산을 수행해도 행공간이 보존된다. 그러나 기본행연산 결과 열벡터의 계수가 달라지므로 열공간은 보존되지 않는 것을 볼 수 있다. 즉, C(A)와 C(R)은 다른 열공간이다.
- 단, A와 R의 rank는 동일하다. 이는 기본행연산으로 열벡터들의 구체적인 값은 변경될 수 있지만, 열벡터들 간의 선형 독립성은 보존된다는 것을 의미하며, 기본행연산이 열공간의 차원은 변경하지 않는다는 것이다. 즉, 열공간의 기저의 개수는 동일하게 유지되므로 dimC(A)=dimC(R)
■ 이 예시에서 행공간의 기저는 첫 번째 행과 두 번째 행이다. 기본행연산 결과 세 번째 행의 모든 성분이 0이 된다는 것은 첫 번째 행과 두 번째 행의 선형 결합으로 세 번째 행을 만들 수 있다는 것이므로 세 번째 행은 공간을 생성할 때 아무것도 기여하지 않는다.
- 그러므로 이 예시에서 행공간의 기저는 [1 0 1 1]과 [0 1 1 0]이라고 할 수 있다.
■ 다음으로 left nullspace N(AT)는 AT의 영공간이다. 영공간에 있는 벡터를 y라고 했을 때 ATy=0이다.
■ ATy=0은 다음과 같이 행렬과 열벡터의 곱이 0이 되는 상태이다.

■ 여기서 y를 왼쪽에 두고 싶으면 방정식 ATy=0를 전치시키면 된다.
- 0은 0T와 동일하므로 ATy=0T라고 할 수 있다.
■ (ATy)T=0T⇔yTATT=0T이며 ATT=A이므로 방정식을 전치시킨 결과는 yTA=0T가 되며, 행벡터와 행렬을 곱하는 형태가 된다.

- 이렇게 ATy=0 방정식을 전치하면 해가 되는 y는 식의 왼쪽에 위치하기 때문에 left nullspace라고 부른다.
■ 이러한 ATy=0에서 어떻게 N(AT)의 기저는 가우스-조던 소거법을 활용하여 얻을 수 있다.
- 가우스 조던 소거법은 다음과 같이 원래 행렬에 단위행렬을 붙여 소거를 진행해서 E행렬(Elimination Matrix)를 만드는 것이다. 이때 A의 역행렬이 존재하면 E행렬이 A의 역행렬이 된다.

- 여기서 EA=R이 성립하며, E는 A−1이 된다.
■ 예를 들어 행렬 A가 다음과 같을 때,
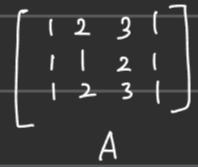
기약행사다리꼴행렬 R을 만들기 위한 소거 과정을 진행하면

이를 EA=R형태로 표현하면 다음과 같다.

■ 이 예에서 A의 rank = 2이고 left nullspace의 차원은m−r이므로 N(AT)=3−2=1차원임을 알 수 있다.
■ 그리고 위의 EA=R에서 left nullspace에 대한 기저를 확인할 수 있다. 바로 E의 세 번째 행이다.
■ 그 이유는 R의 세 번째 행의 원소는 모두 0. 즉, 영벡터이다. 영벡터가 존재한다는 것은 A 벡터의 선형 결합으로 영벡터를 만들 수 있다는 의미이며,
■ 이 예시에서 R의 세 번째 행의 성분을 모두 0으로 만드는 선형 결합은 다음과 같이 A의 행벡터와 E의 세 번째 행의 계수를 이용한 선형 결합이다.

■ 이렇게 영벡터를 만드는 과정은 yTA=0T와 동일하다. 즉, yT=[−101]이며 이것은 R행렬에서 모든 성분이 0인 행에 대응되는 E행렬의 행이다.
'선형대수' 카테고리의 다른 글
| Orthogonal vectors and subspaces (0) | 2025.02.10 |
|---|---|
| Matrix spaces; rank 1 (0) | 2025.02.04 |
| Independence, basis, and dimension (0) | 2025.02.04 |
| Solving Ax = b: row reduced form R (0) | 2025.02.04 |
| Solving Ax = 0: pivot variables, special solutions (0) | 2025.02.04 |



