1. 순환 신경망(Recurrent Neural Network, RNN)
■ 시계열 데이터에 더 나은 예측을 하기 위해 과거 시점의 정보를 현재 시점에 반영하는 순환 신경망(Recurrent Neural Network, RNN)은 피드포워드 신경망과 달리 다음과 같이 순환 경로가 존재한다.
1.1 RNN 구조

■ xt가 입력층의 입력 벡터라고 할 때, 각 단어의 분산 표현은 xt이며, x0,x1,⋯,xt,⋯가 순서대로 하나씩 RNN 계층에 들어간다.
■ 위와 같은 순환 구조를 시점(time step) 기준으로 펼치면, 다음과 같이 한 방향으로 연산이 수행되는 피드포워드 신경망으로 볼 수 있다.

- RNN을 표현할 때, 위의 그림에서 좌측과 같이 화살표로 순환 구조를 그려 재귀 형태로 표현하기도 하지만, 우측과 같이 여러 시점으로 펼쳐서 표현하기도 한다.
- 두 표현 방법도 동일한 RNN을 표현하고 있는 것이다. 단지 재귀 형태로 표현하느냐, 시점의 흐름에 따라 표현하느냐의 차이이다.
■ 위의 구조와 같이 각 시점의 RNN 계층은 t−1 시점의 출력 결과 ht−1과 t 시점의 입력 xt를 통해 t 시점의 출력 ht를 계산한다. 즉, 과거 시점의 정보를 현재 시점에 반영한다. 이때 수행되는 계산의 수식은 다음과 같다.
ht=tanh(ht−1Wh+xtWx+b)
- ht−1과 xt는 벡터, b는 편향
- ht−1Wh+xtWx+b의 결과에 tanh 함수를 적용시켜 시점 t의 출력 ht로 변환한다.
- 은닉층에서 활성화 함수를 통해 결과를 출력하는 노드를 셀(cell)이라고 한다. RNN에서 이 셀은 과거 시점의 값을 기억하는 일종의 메모리 역할을 수행해서 RNN 계층을 메모리 셀 또는 RNN 셀이라고 부른다.
■ 위의 그림과 같이 RNN 셀이 출력층 방향으로 또는 다음 시점으로 보내는 h의 값을 은닉 상태(hidden state) (벡터)라고 부른다.
- 예를 들어, h0은 t=0 시점의 은닉 상태 벡터, ht+1은 t=t+1 시점의 은닉 상태 벡터
■ 현재 시점이 t일 때, t 시점의 RNN 계층의 입력은 2개이다.
- (1) 하나는 입력층에서 전달되는 xt(정확하게는 입력층의 가중치와 곱해진 Wxxt)
- (2) 다른 하나는 바로 전 시점의 RNN 계층에서 오는 ht−1(정확하게는 RNN 계층의 가중치와 곱해진 Whht−1)
- 이때의 ht−1도 위의 입력값들을 기반으로 계산된 값들이다.
- 즉, ht−1은 h0부터 ht−2의 정보가 압축되어 전달된 값으로 볼 수 있다.
■ 그러므로, 은닉 상태 ht가 t=0부터 t=t−1 시점까지의 입력에 대한 정보를 계승한 것으로 볼 수 있다. 이러한 특징 때문에 RNN 계층이 메모리(기억력) 역학을 수행한다고 말할 수 있는 것이다.
■ 그리고 순환 구조이므로 ht는 (출력층으로 향하는) 다음 계층으로 전달되는 동시에 자기 자신의 RNN 계층으로도 전달된다.
■ 이때, RNN 계층의 다음 계층이 출력층 yt라고 한다면, yt=f(Wyht+b)로 계산될 것이다.
- Wy는 ht에서 yt로 향할 때 곱해지는 가중치
- f는 비선형 활성화 함수 ex) softmax
■ RNN 계층에서 입력층의 입력 벡터 xt를 입력 받아, 은닉 상태 벡터 ht를 계산하고 출력층의 출력 벡터 yt를 계산하는 과정을 수식으로 나타내면 다음과 같다.
ht=tanh(Whht−1+Wxxt+b), yt=f(Wyht+b)
- 위의 수식에서 사실상 학습이 되는 부분은 가중치 매개변수 Wh,Wx,Wy이다.
- Wh,Wx,Wy는 매 시점(time step)마다 공유하는 구조이다. 즉, 매 시점 가중치 매개변수는 값이 동일하다.
- 예를 들어 t−1 시점의 Wh는 t 시점 t+1 시점, ... t+k 시점의 Wh와 동일한 값을 갖는다.
- Wx와 Wy도 마찬가지이다.
■ 이 과정을 그림으로 나타내면 다음과 같다.

■ 자연어 처리 문제에서 사용하던 RNN은 텍스트를 순차적으로 하나씩 입력하는 형태이다. 위의 그림에서 x1,x2,x3,⋯,xt,⋯은 텍스트의 토큰이다.
- 예를 들어 xt 가 I am a student라고 할 때, xt를 구성하는 단어(토큰)이 'I', 'am', 'a', 'student'라고 하자.
- 이때, 'I'가 입력 단어(토큰) x1, 'am' 이 x2, 'a' 는 x3, 'student'는 x4에 해당된다.
■ 입력 벡터 xt를 단어 벡터라고 했을 때, 이 단어 벡터의 차원을 d라고 하자. 그리고 은닉 상태의 크기를 Dh라고 한다면,
xt를 열벡터로 간주했을 때 xt의 크기는 d×1, 은닉 상태인 ht,ht−1의 크기는 Dh×1이다. 이를 통해 나머지 가중치 행렬과 편향의 크기를 다음과 같이 유추할 수 있다.

■ RNN은 입력과 출력의 길이를 다르게 설계할 수 있어 다양한 용도로 사용할 수 있다.
- ① one-to-many: 하나의 입력에 대해 여러 개의 출력을 하는 모델
- ex) 하나의 이미지 입력에 대해서 이미지 속 내용을 설명하는 글을 만들어내는 이미지 캡셔닝(image captioning) 등
- 생성되는 출력은 시퀀스이다. 내용을 설명하는 글이므로, 단어들의 나열이기 때문이다.
- ② many-to-one: 단어 시퀀스를 입력으로 받아 하나의 출력을 하는 모델
- ex) 댓글이 악플인지 아닌지, 메일이 스팸 메일인지 정상 메일인지 분류하는 sentence classification, 감성 분류(sentiment classification) 등
- ③ many-to-many(token-by-token, encoder-decoder): 여러 개의 토큰을 입력으로 받아 여러 개의 토큰을 출력하는 모델
- 문장의 모든 토큰에 대한 품사를 예측하는 품사 태깅(pos tagging)이나 개체명 인식, 챗봇, 번역기 등

- 시퀀스 데이터를 다룰 경우 단순한 one-to-one이 아닌 many-to-one 또는 one-to-many 또는 many-to-many(token-by-token 또는 encoder-decoder) 구조를 사용하게 된다.
1.2 RNN 계층의 순전파와 역전파
■ RNN의 순전파 결과인 ht의 식은 ht=tanh(ht−1Wh+xtWx+b)이다.
■ 만약, 데이터를 미니배치로 모아서 처리한다면 xt와 ht의 행 방향에 각 샘플이 저장된다.
■ 위에서 계산한 ht=tanh(ht−1Wh+xtWx+b) 계산에서의 형상은 미니배치의 수가 1일 때이다.
■ 미니배치 크기가 N, 입력 벡터의 차원 수가 D, 은닉 상태 벡터의 차원 수가 H라고 할 때, 미니배치를 고려한 ht=tanh(ht−1Wh+xtWx+b) 계산에서의 형상은 다음과 같다.

■ 이러한 RNN 순전파 계산 과정을 계산 그래프로 나타내면 다음과 같다.
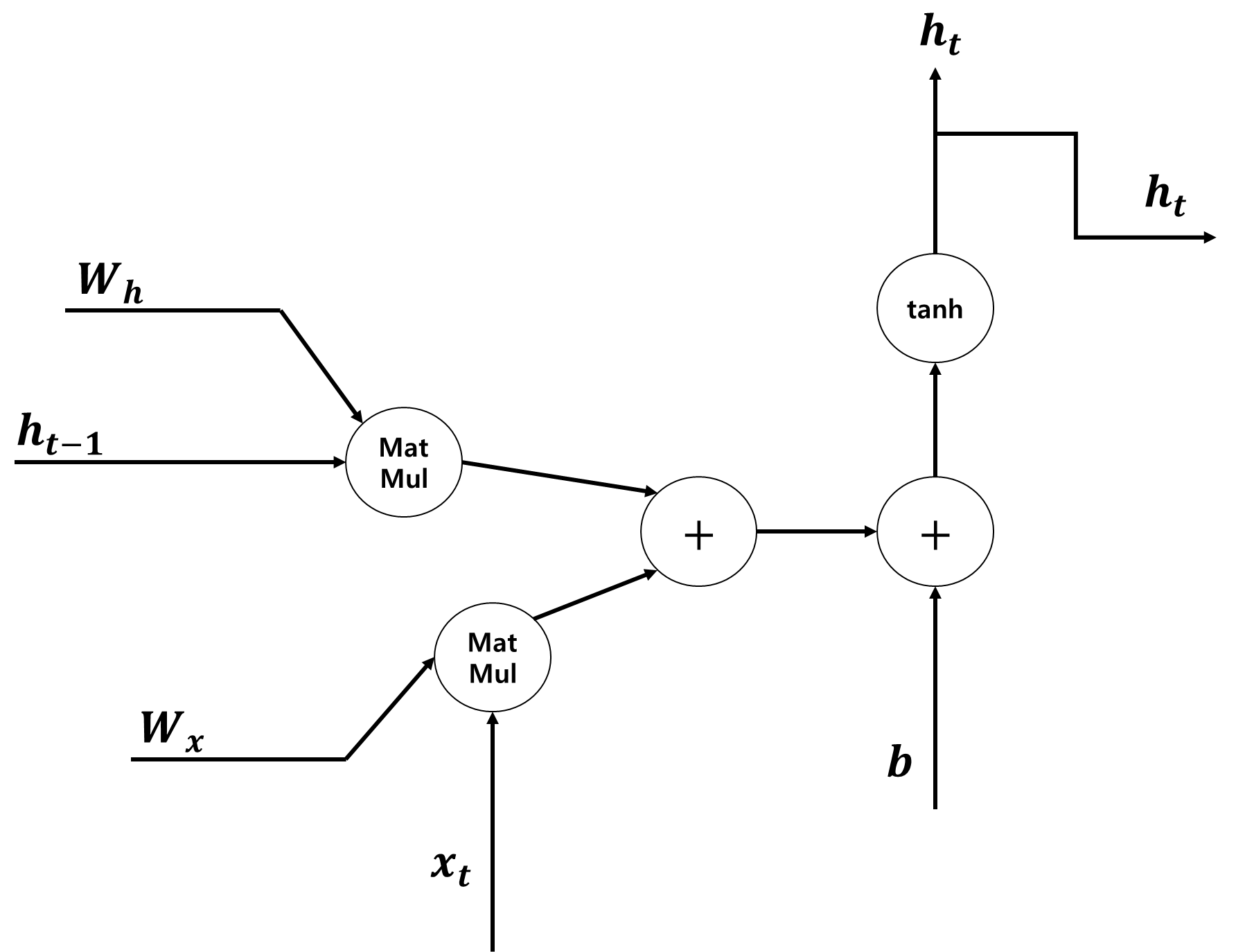
■ 미니배치로 처리할 경우 xtWx의 계산은 행렬곱, ht−1Wh의 계산도 행렬곱이다. 그러므로 RNN 계층의 순전파 계산 그래프에서 수행되는 연산은 행렬곱, 덧셈, 하이퍼볼릭 탄젠트. 3개의 연산으로 구성된다.
- 미니배치 차원을 포함한 RNN 수식에서 xtWx, ht−1Wh의 결과는 어떤 2차원 형태가 된다.
- 이때, 1차원 편향 벡터 b는 ht−1Wh+xtWx에 더하려면 차원이 맞지 않으므로, 자동으로 b를 해당 차원에 맞추는 브로드캐스트 연산이 발생한다.
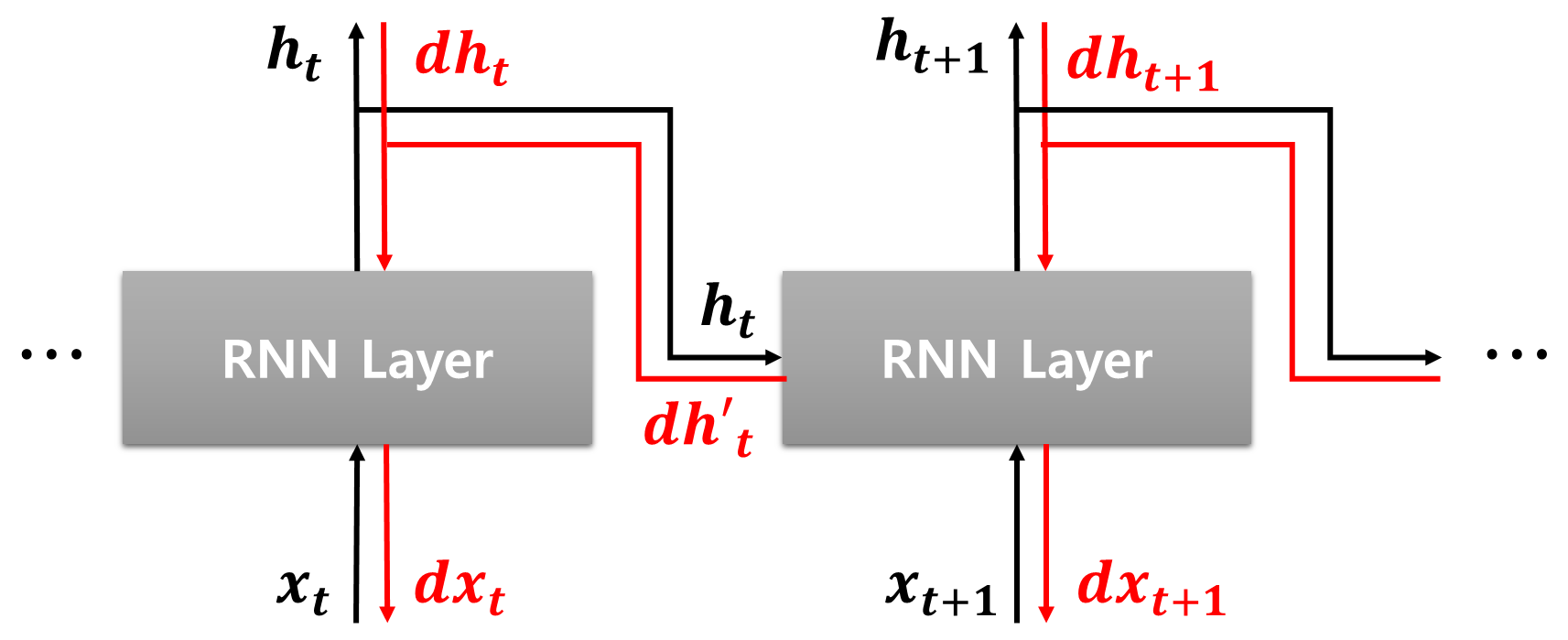
■ t 시점의 순전파 결과인 ht는 다음 층과 다음 시점인 t+1 시점(time step)의 RNN 계층의 입력으로 들어간다. 이렇게 RNN 계층의 순전파에서는 출력 ht가 2개로 분기된다.
■ 그러므로 t번째 RNN 계층에 분기된 순전파 결과는 역전파 과정에서 다음 그림과 같이 다음 층에서 전파된 기울기를 dht, t+1 시점에서 전파된 기울기를 dh′t라고 했을 때, 합산된 기울기 (dht+dh′t)가 입력으로 들어간다.
1.3 BPTT(Backpropagation Through Time)
■ 위의 그림처럼 RNN 계층은 순환 구조를 시간축으로 펼치면 일반적인 신경망의 구조(피드포워드 신경망 구조)이기 때문에 다음과 같은 순서로 학습(순전파 & 역전파)을 진행할 수 있다.
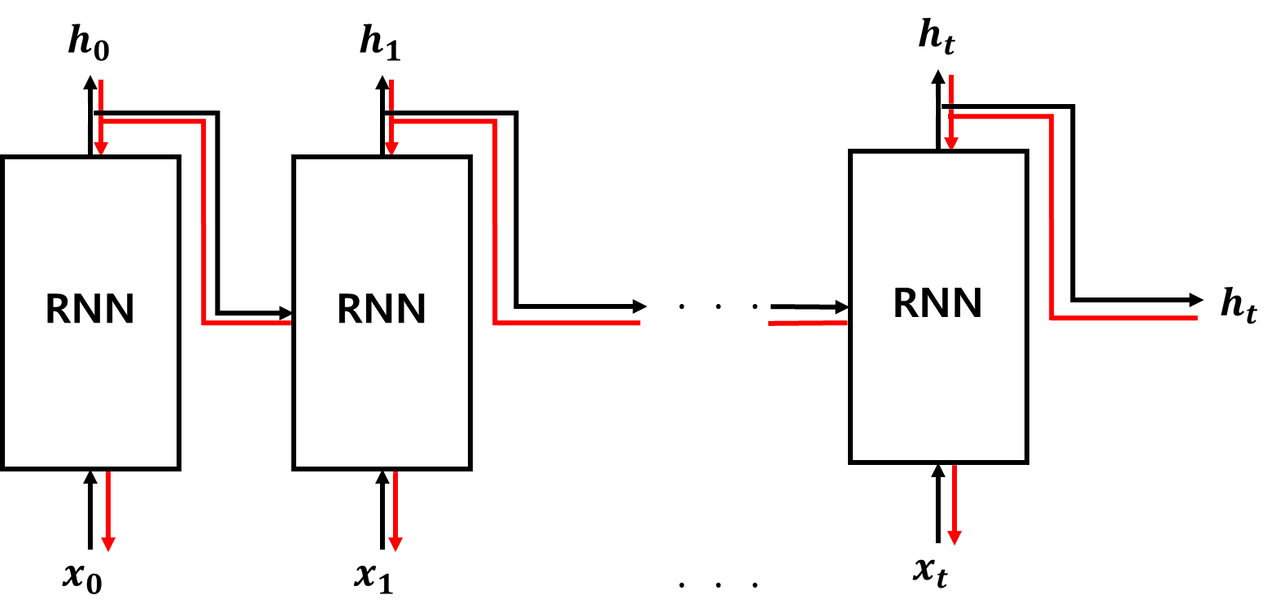
■ 이때의 오차역전파는 단순 신경망을 학습시키기 위해 사용했던 오차역전파와는 다르게 '시간 방향으로 펼친 신경망'을 학습시키기 위한 오차역전파이다. 이 알고리즘을 BPTT라고 한다.
■ 시간을 통한 역전파(Backpropagation Through Time, BPTT)는 엘만 네트워크(Elman network)와 같은 순환 신경망(RNN)을 훈련하기 위한 기울기(gradient) 기반 기법이다.
■ 예를 들어, 다음과 같이 입력이 3개이고 출력이 1개인 many-to-one 구조일 때, 순전파 과정은 다음과 같이 하나의 예측값 ˆy를 계산해서 실제값(target)인 y와의 비교를 통해 손실(Loss)값을 계산한다.
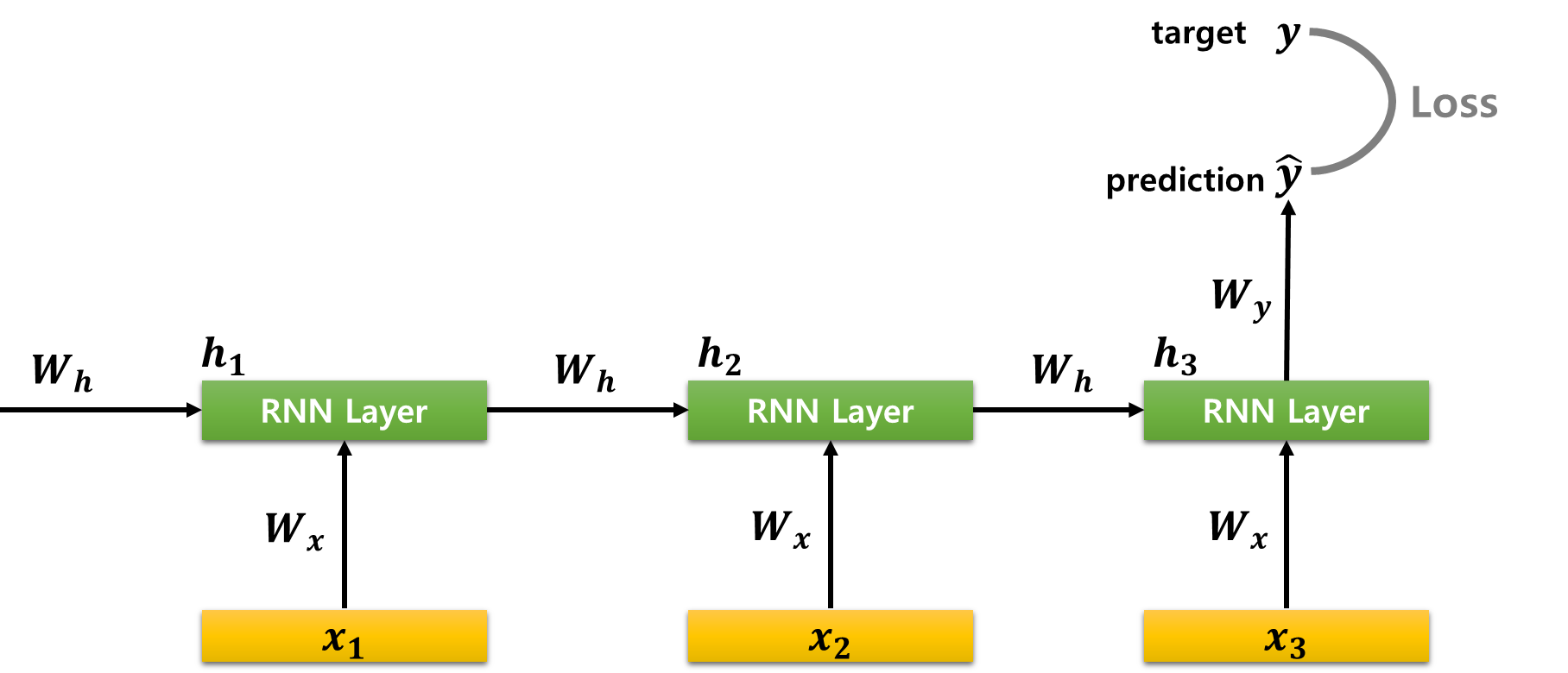
■ 이때의 역전파는 BPTT에 따라 다음과 같이 진행된다.
■ 먼저, 기억해야 할 것은 이 예시의 RNN 형태는 folded RNN을 시간의 흐름에 따라 펼친 형태이며, 각 층의 가중치인 Wx,Wy,Wh는 학습의 대상이며(업데이트할 매개변수이며), Wx,Wy,Wh라는 각각의 가중치 행렬은 모든 시점에서 동일한 파라미터 값을 공유한다.
- 예를 들어, t=1,2,3 시점의 Wx은 동일한 값이다. Wy,Wh도 마찬가지이다.
■ 즉, 업데이트해야 할 가중치 행렬은 입력층과 RNN 계층을 연결해주는 Wx, RNN 계층에서 직전 시점에서 다음 시점의 은닉 상태를 연결하는 Wh이며, Wy이다.
- 이 예에서 Wy는 예측값 1개를 연결하기 위한 가중치 행렬이다.
■ 시간 순서에 따라 손실(Loss)에 대한 Wy의 미분부터 계산해야 한다.
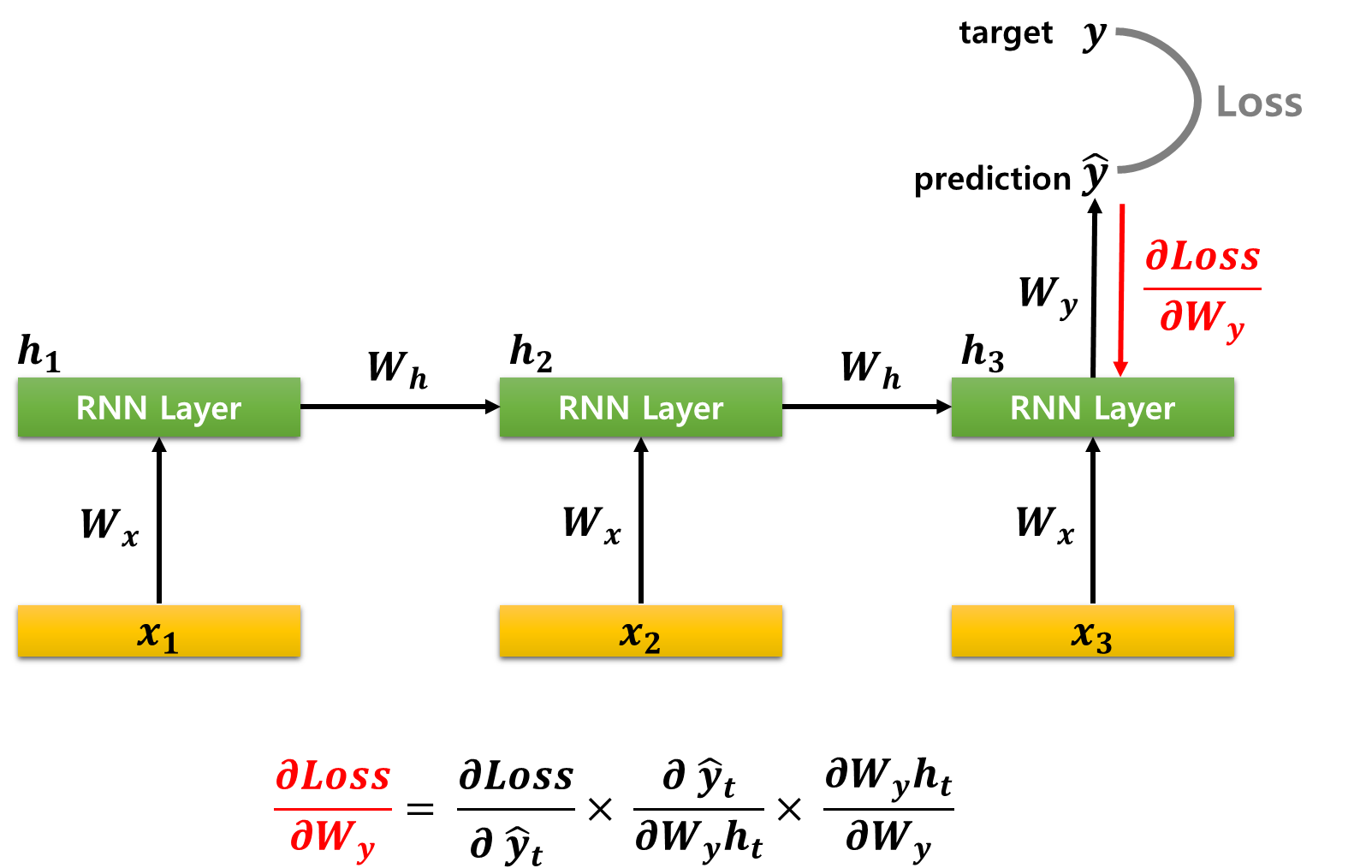
■ ∂Loss∂Wy를 계산하기 위해 체인 룰(chain rule)을 이용한다면,
- ˆy는 ˆy=activation(Wyht)로 계산된다. (편향은 생략)
- 이 계산은 먼저 ht에 가중치 행렬 Wy를 곱해서 Wyht를 얻고, 그 결과에 활성화 함수를 적용하여 ˆy를 산출한 뒤, 이 ˆy를 기반으로 Loss값을 계산하는 방식이다.
- 역전파에서는 순전파에서 진행한 계산의 순서를 반대로 따라가기 때문에 체인 룰을 뒤집에서 적용할 수 있다.
- 구체적으로는 다음과 같이 진행된다.
- (1) 손실 Loss에서 출력 ˆyt에 대한 기울기. 즉 ∂Loss∂ˆyt를 계산하고,
- (2) 이후 출력 ˆyt에서 Wyht로의 미분 ∂ˆyt∂Wyht를 구하며
- (3) 마지막으로 Wyht에서 가중치 Wy에 대한 미분 ∂Wyht∂Wy를 계산한다.
- 그러므로 ∂Loss∂Wy는 다음과 같은 체인 룰로 나타낼 수 있다.
∂Loss∂Wy=∂Loss∂ˆyt⋅∂ˆyt∂Wyht⋅∂Wyht∂Wy
■ 이 예에서는 입력이 3개 출력이 1개인 many-to-one이므로 ∂Loss∂Wy는 시점 t=3에서의 영향만 고려하면 된다. 그러나, Wh와 Wx는 매 시점마다 사용된다.
■ 먼저, Wh의 경우 시점 t=3에서의 역전파 ∂Loss∂Wy가 전파될 때, h3가 h2로부터, 또 h2가 h1로부터 영향을 받았으므로 이를 고려하여 미분해야 한다.
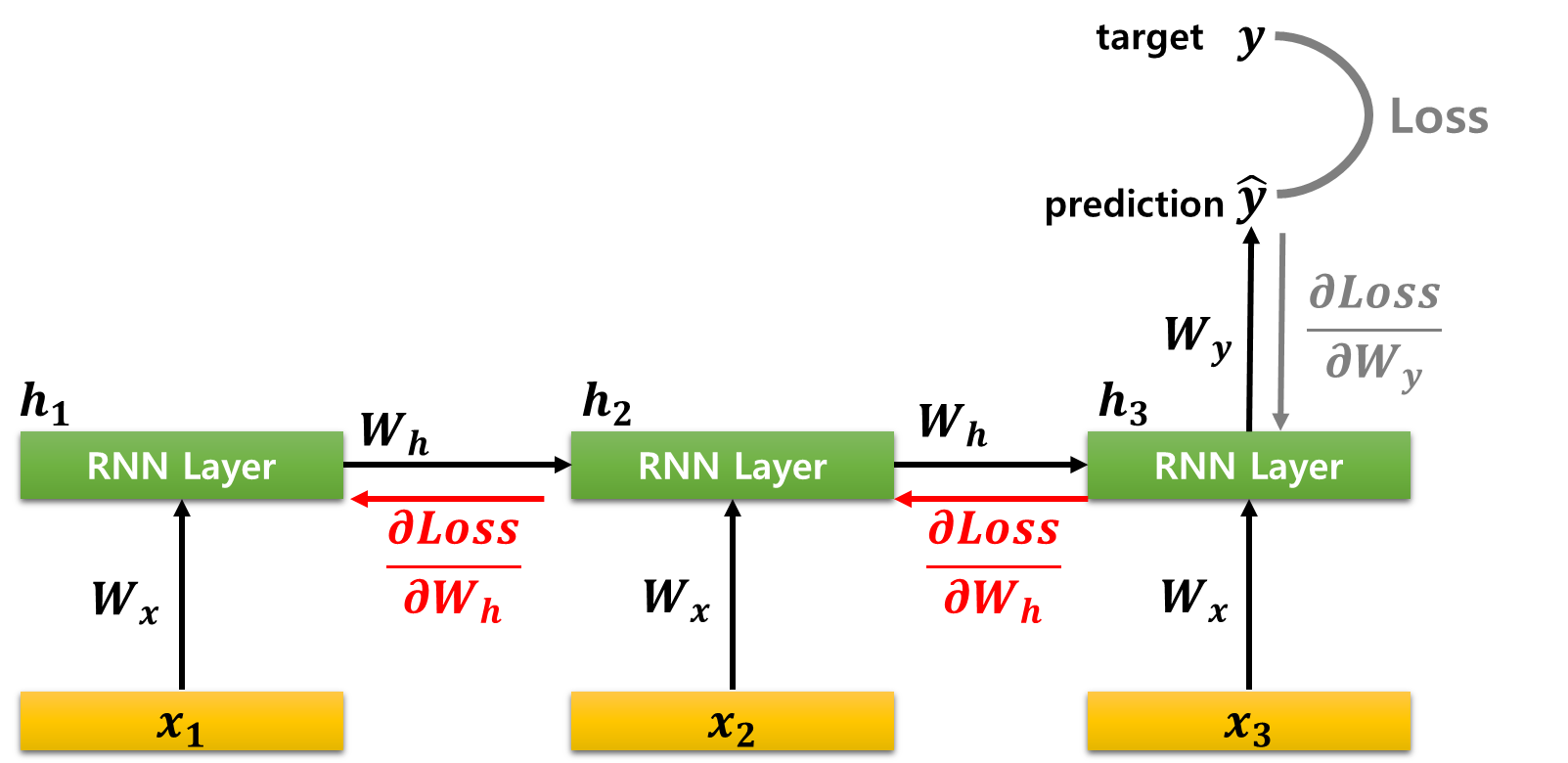
■ 먼저 t=3에서의 시점 t=3에서의 역전파 ∂Loss∂Wy=∂Loss∂ˆyt⋅∂ˆyt∂Wyht⋅∂Wyht∂Wy가 전파된다.
∂Loss∂Wh=∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂Wh+∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂Wh+∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂h1×∂h1∂Wh
- 먼저, t=3일 때의 Wh에 대하여 Loss를 구하면, ∂Loss∂Wh=∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂Wh이다.
- 그리고 h3은 h2로부터 영향을 받기 때문에(의존적이기 때문에) 이전 시점(time step)에 대한 영향을 고려할 필요가 있다.
- h3가 h2로부터 전해진 영향을 고려해 기울기를 계산한 것이 ∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂Wh이다.
- 마찬가지로 h2가 h1로부터 영향을 받는다. 이를 고려해 기울기를 계산한 것이 ∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂h1×∂h1∂Wh이다.
■ 은닉 상태 ht=activation(Whht−1+Wxxt)는 재귀때문에 한 시점(의 오차가 이전 시점에까지 영향을 거슬러 올라가며 Wh와 연결된다.
■ 이렇게 BPTT에서는 현재 시점뿐 아니라 이전 시점까지, 다시 이전 시점에서 그 직전 시점까지... . 이런 식으로 시점을 거슬러 올라가며 모든 시점에 대한 역전파를 더해주는 것이 된다.
■ Wx도 마찬가지로 매 시점에서 ht=activation(Whht−1+Wxxt)에 사용된다. 입력 xt가 시점 t의 은닉 상태 ht에 영향을 주고, 또 ht는 이전 시점의 ht−1 그리고 예측 ˆyt에 모두 연결된다. 그러므로 ∂Loss∂Wx는 다음과 같다.
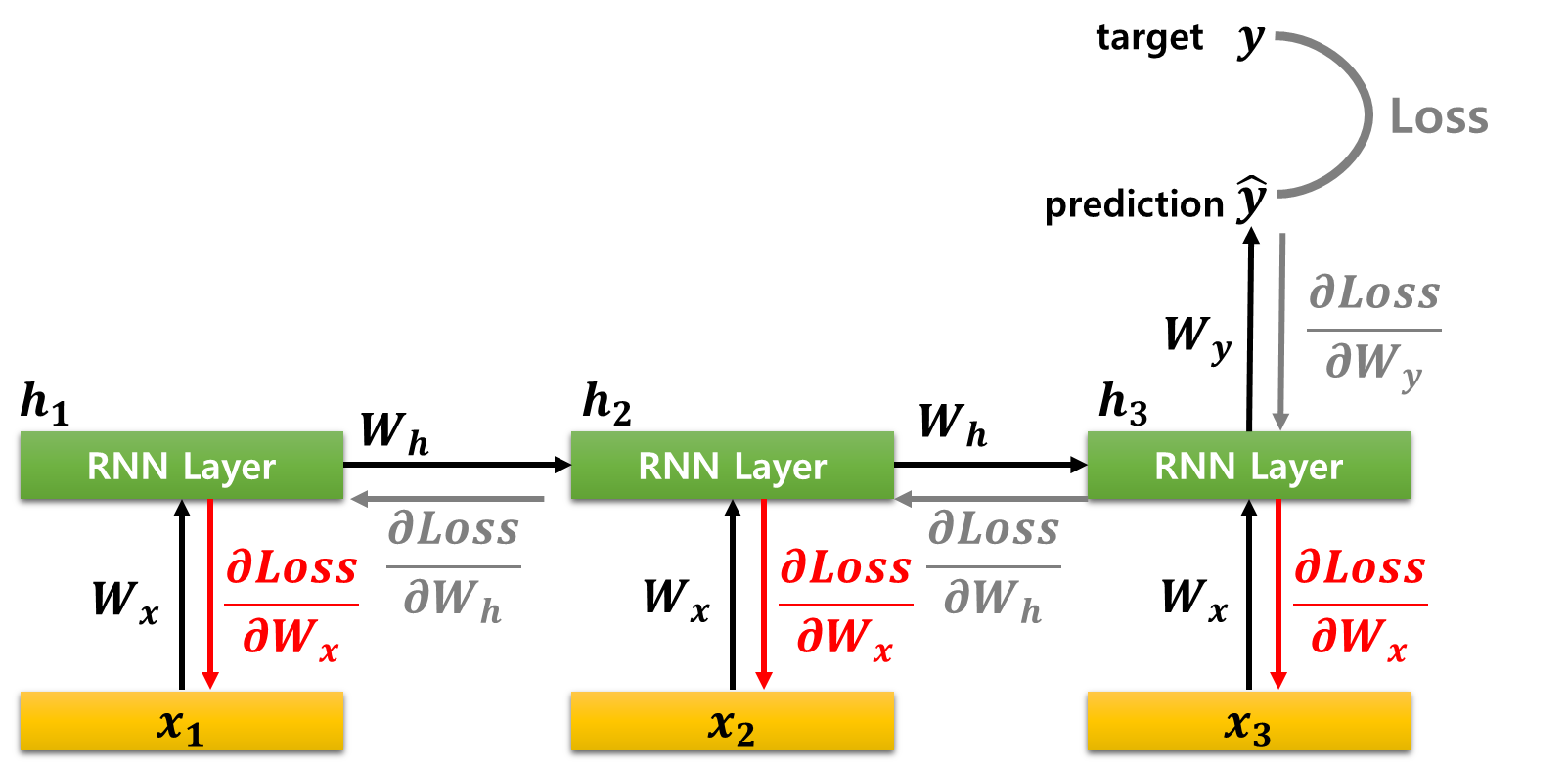
∂Loss∂Wx=∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂Wx+∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂Wx+∂Loss∂ˆyt×∂ˆyt∂h3×∂h3∂h2×∂h2∂h1×∂h1∂Wx
- 덧셈을 기준으로 첫 번째 항이 t=3에서의 영향, 두 번째 항과 세 번째 항이 t=3,t=2로부터 전해진 영향을 고려했을 때, 체인 룰로 나타낸 것이다.
- 시점별 xt=1,2,3으로부터 기인한 경로가 각각 더해진 것으로 볼 수 있다.
- ∂Loss∂Wh와 ∂Loss∂Wx는 "시점별 오차 기여"를 모두 더한 값이 된다.
- 시점이 t=0부터 t=t까지라면, 위의 ∂Loss∂Wy 그리고 ∂Loss∂Wh와 ∂Loss∂Wx는 다음과 같이 나타낼 수 있다.
∂Loss∂Wy=∂Lt∂ˆyt×∂ˆyt∂Wyht×∂Wyht∂Wy
∂Loss∂Wh=t∑k=0(∂L∂ˆyt×∂ˆyt∂ht×∂ht∂hk×∂hk∂Wh)
∂Loss∂Wx=t∑k=0(∂L∂ˆyt×∂ˆyt∂ht×∂ht∂hk×∂hk∂Wx)
■ 각 파라미터에 대한 손실 기울기인 ∂Loss∂Wy, ∂Loss∂Wh, ∂Loss∂Wx는 각각의 파라미터가 모델의 손실 함수에 기여하는 정도를 나타낸다.
■ 즉, 이 기울기 값들은 각 파라미터가 얼마나 업데이트되어야 하는지를 의미한다.
■ 그러므로 학습률(learning rate)이 η라고 했을 때, 각 파라미터는 다음과 같이 기여도(손실 기울기)에 따라 업데이트된다.
Wy=Wy−η⋅∂Loss∂Wy, Wh=Wh−η⋅∂Loss∂Wh, Wx=Wx−η⋅∂Loss∂Wx
1.4 RNN의 단점
■ BPTT를 이용해 RNN을 학습할 때 큰 시계열 데이터(시간 크기가 큰 데이터)를 사용하면, 시퀀스의 크기에 비례해 메모리 사용량이 증가한다는 문제와 역전파 과정에서 기울기가 불안정해지는 문제가 있다.
■ 각 시점에서 영향을 받은 것에 대한 미분을 모두 고려하여 더한다. 이때, tanh함수를 많이 통과하기 때문에 마지막 시점에서 시작된 기울기가 첫 번째 시점까지 역전파되는 과정에서 소실될 수 있다.
■ 현재 시점이 받게 되는 과거 시점의 정보 ht−1은 더 먼 과거 시점들의 정보( ht−2 부터 h0 )가 압축되어 있는 상태이다. 즉, 의존적이다. 그래서 Wh에 대한 손실 기울기를 계산할 때, 체인 룰을 통해 각 시점에 대한 영향(또는 경로)을 모두 고려하였다.
■ ht는 순전파 과정에서 ht=tanh(Whht−1+Wxxt)로 계산된다.
■ 이때의 하이퍼볼릭 탄젠트 함수 tanh(x)=ex−e−xex+e−x는 다음과 같이 -1과 1사이의 값을 가지므로 Whht−1+Wxxt의 값을 -1과 1사이의 어떤 값으로 반환하게 된다.
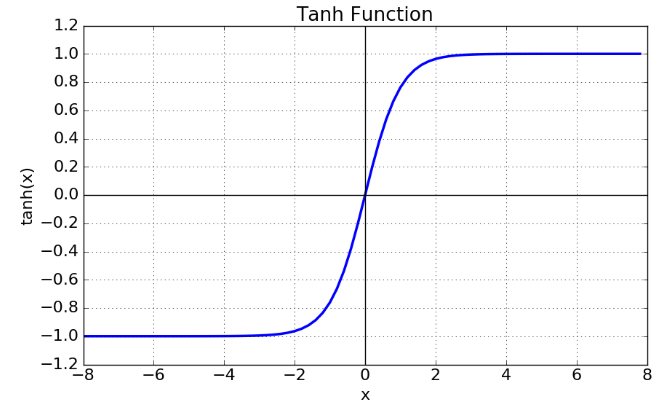
■ 역전파 과정에서 하이퍼볼릭 탄젠트 함수의 미분 tanh′(x)=1−tanh2(x)은 다음과 같이 0과 1 사이의 값을 갖는다.
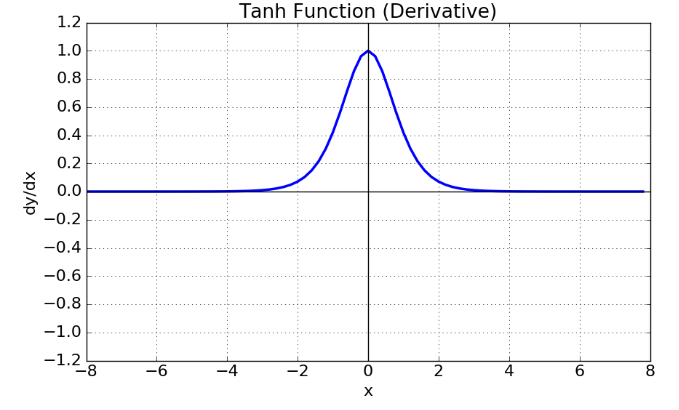
■ ht=tanh(Whht−1+Wxxt)이므로 ∂ht∂ht−1=tanh′(Wxxt+Whht−1)⋅Wh이 된다.
- ht=tanh(Whht−1+Wxxt)에서 안 쪽의 선형 결합을 at=Whht−1Wxxt로 두면, ht=tanh(at)이다.
- ht=tanh(at)이고 at=Whht−1Wxxt이므로, ht=tanh(at)라는 합성 함수를 at와 ht−1 사이의 관계로 풀어보면, ht−1→at→ht이다.
- 따라서 체인 룰을 적용하면 ∂ht∂ht−1=∂tanh(at)∂at⋅∂at∂ht−1이며
- 첫 번째 항 ∂tanh(at)∂at=tanh′(at)가 되고
- 두 번째 항은 at=Whht−1Wxxt식에서 ht−1에 대한 편미분이므로 ∂at∂ht−1=Wh이다.
- 결과적으로 ∂ht∂ht−1=tanh′(at)⋅Wh=tanh′(Whht−1+Wxxt)⋅Wh가 된다.
■ 그러므로 ∂Loss∂Wh의 식에 포함된 "현재 시점과 이전 시점의 영향에 대한 미분(현재 시점과 이전 시점의 의존으로 인하여 계산하게 되는 미분)" ⋯∂h5∂h4⋅∂h4∂h3⋅∂h3∂h2와 같은 ∂ht∂ht−1=tanh′(Wxxt+Whht−1)⋅Wh값들이 0과 1사이의 값을 가지게 된다.
■ 0과 1사이의 값을 여러 번 곱할수록 0에 가까운 값이 된다. 그래서 시퀀스의 길이가 길어질수록, BPTT를 통해 역전파를 계산하는 RNN은 기울기 소실이 발생하기 쉽다.
- 입력 데이터의 길이가 곧 총 시점의 수(time steps)
■ 이와 같은 기울기 소실 문제는 "장기 의존성(long-term dependency) 문제"를 야기한다. RNN이 과거 시점의 정보를 현재 시점까지 전달할 때, 시퀀스가 길어질수록 과거 정보가 손실되거나 왜곡되는 것을 말한다.
■ 예를 들어, 멀리 떨어진 단어들 간의 관계를 학습해야 하는 언어 모델링 작업에서 RNN은 이러한 문제로 과거 정보를 연결하지 못할 수 있다.
■ RNN은 짧은 시퀀스에서는 잘 작동하지만, 긴 시퀀스에서는 유의미한 장기 의존성을 학습하기 어렵다. 이를 개선하기 위한 방법으로 일정 시점에 대해서만 부분적으로 업데이트하는 Truncated BPTT가 있으며, LSTM이나 GRU같은 개선된 아키텍처가 등장했다.
■ 그리고 이러한 순환 신경망의 단점은 자연어 처리에서 입력(토큰)을 순차적으로 처리해야 하기 때문에 시퀀스가 길어질수록 학습 속도가 느려지고, 먼저 입력한 토큰의 정보가 희석되면서 성능이 떨어진다는 문제점도 있다. 이 문제를 해결하기 위해서 층을 깊게 쌓는 방법을 고려할 수 있지만, RNN 층을 깊게 쌓으면 위와 같은 체인 룰에 의해 기울기가 올바른 방향으로 계산되지 못해 학습이 불안정해진다.
cf) 트랜스포머는 이런 RNN의 문제를 해결하기 위해 입력을 하나씩 순차적으로 처리하는 방식 대신 셀프 어텐션(self-attention)을 도입했다.
1.5 Truncated BPTT
■ RNN이나 LSTM같은 순환 구조를 가진 신경망은 시점(time step)을 펼치면 일반적인 피드포워드 신경망 형태로, 오차 역전파는 BPTT 방식을 통해 학습한다.
■ 하지만 BPTT 방식은, 긴 시퀀스를 펼쳐서 학습할 경우 메모리 사용량이 커지며, 훈련 시간이 길어질 뿐만 아니라, 기울기 소실(gradient vanishing)이나 폭발(gradient exploding)이 발생하기 쉽다는 문제점이 있었다.
■ 이러한 문제를 개선하기 위해 Truncated BPTT는 전체 시퀀스를 한 번에 처리하는 대신, 일정한 길이로 나누어서 학습함으로써 BPTT를 '부분적으로'만 수행한다. 이는 전체 데이터를 미니배치로 학습하는 방식과 유사하다.
■ 시퀀스가 매우 길어지면 RNN을 펼친 계산 그래프도 길어지며, 이를 처리하기 위해 많은 중간 계산을 저장해야 한다. 또한, RNN의 순차적 입력 특성으로 인해 연산량이 증가하고, 그래디언트(기울기)를 모두 계산하는데 시간이 오래 걸린다.
■ Truncated BPTT는 긴 시퀀스롤 모두 펼치지 않고 일정 길이로 나누어 처리함으로써 메모리 사용량을 절약할 수 있다. 또한, 부분적으로만 역전파를 수행하기 때문에 기울기 소실과 폭발 문제를 완화하는 데 도움을 준다.
■ 예를 들어, time step이 총 30인 시계열 데이터가 있을 때, 이를 10 time step씩 나누어 3개의 시퀀스로 분할할 수 있다. 이는 다음과 같이 하나의 신경망을 3개의 신경망 블록으로 나눈 것으로 볼 수 있다.

■ 단, 순전파 과정에서는 은닉 벡터를 통해 블록 간 연결을 유지하며, 역전파 과정에서만 은닉 벡터의 연결을 끊고 각 블록 내에서 역전파를 수행한다.
■ 예를 들어, 위의 그림은 RNN 계층을 10개씩 잘라내 3개의 신경망 블록을 만들었다. 그러므로 역전파 과정에서만 각 블록은 다른 블록과 독립적으로 10 time step단위로 오차 역전파를 수행한다. 즉, 파라미터 업데이터는 3개 블록 각각 진행되는 것이다.


■ 중요한 것은 전파 흐림이 역전파 과정에서만 끊긴다는 것이다.
■ 예를 들어, 위의 그림에서 순전파 과정에서는 첫 번째 블록의 순전파 결과인 은닉 상태 벡터 h9는 두 번째 블록에 전달되고, 두 번째 블록의 순전파 결과인 은닉 상태 h19는 세 번째 블록에 전달된다.
■ RNN의 Truncated BPTT 방식은 이런 식으로
- (1) 각 블록의 '입력 데이터(시계열 데이터)를 순서대로 넣고',
- (2) 이전 블록의 은닉 상태를 계승해서 '순전파의 흐름만 마지막 블록까지 계속 연결하고',
- (3) '오차 역전파는 각 블록 내에서 독립적으로 수행'한다.
■ Truncated BPTT의 단점은 '시퀀스 하나'를 '서브 시퀀스 여러 개'로 나누었기 때문에, 앞뒤가 끊긴 부분에서 의존 정보가 끊길 수 있다.
■ 즉, 시퀀스가 잘리 지점에서 발생하는 정보 손실로 인해 장기 의존성을 학습하기 어렵다는 한계가 있다.
참고) 파이토치에서는 detach() 메서드로 텐서를 복사하면, 복사된 텐서는 원본 텐서와 메모리는 공유하지만, 계산 그래프에서 텐서의 requires_grad를 False로 만들 수 있다.
- 예를 들어 다음과 같은 계산 그래프가 있다고 했을 때,

- 첫 번째 계층에서 출력된 out1에 detach( )를 적용하면, out1 텐서의 requires_grad = False로 변경되어 역전파 과정에서 다음과 같이 out2에서 전달되는 기울기가 이전 계층으로 흘러가지 않는다.

1.5.1 Truncated BPTT의 미니배치 학습
■ Truncated BPTT 기법도 입력 데이터를 '순서대로'넣는 방식이다.
■ 위의 예시에서는 미니배치 수가 1일 때의 과정이다. 위의 예시처럼 미니배치 수가 1일 때, 길이가 1,000인 시계열 데이터를 한 번에 처리한다면 필요한 시점은 t=1,2,⋯,1000이다.
■ 만약, 길이가 1,000인 시계열 데이터를 10 time steps씩 자르는 Truncated BPTT 방법을 사용한다고 했을 때,
■ 미니배치 수가 1이라면, 첫 번째 블록에 들어가는 입력 데이터는 x0,x1,⋯,x9, 두 번째 블록에 들어가는 입력 데이터는 x10,x11,⋯,x19, ... 마지막 블록에 들어가는 입력 데이터는 x990,x991,⋯,x999로 총 100묶음이다.
■ 만약, 미니배치 수가 2라면 x0부터 x499까지 50묶음, x500부터 x999까지 50묶음으로 나눌 수 있다.
■ 첫 번째 블록의 첫 번째 미니배치에는 x0,x1,x9, 두 번째 미니배치에는 x500,x501,⋯,x509가 들어가도록 시작 위치를 옮겨서 미니배치 학습을 수행할 수 있다.
- 이렇게 만들면, 두 번째 블록의 첫 번째 미니배치에는 x10,x11,⋯,x19, 두 번째 미니배치에는 x510,x511,⋯,x519가 들어가게 된다.
■ 참고로 BPTT를 사용한다면, x0,x1⋯,x9나 x500,x501,⋯,x509같은 입력 데이터는 시간 정보가 있으므로, t=500,501,⋯,509의 입력 데이터 x500,x501,⋯,x509는 과거 시점의 입력 데이터 x0,x1⋯,x9에 의존적이다. 그러므로 각 데이터의 원소들을 (x9,x0,⋯,x1), (x506,x503,⋯,x509)처럼 셔플을 적용할 수 없다.
■ 단, 미니배치에 있는 입력 데이터 (x0,x1,⋯,x9)와 (x500,x501,⋯,x509)는 독립이다.
- h9를 계산할 때 데이터 (x0,x1,⋯,x9)만 사용하고 h509를 계산할 때는 (x500,x501,⋯,x509)만 사용하기 때문이다.
■ 그러므로 미니배치에 들어 있는 입력 데이터의 순서는 셔플해서 사용해도 무방하다.
2. 깊은 순환 신경망(Deep RNN), 양방향 순환 신경망(Bidirectional RNN)
2.1 깊은 순환 신경망(Deep RNN)
■ 총 시점(time steps)이 T일 때, 입력층과 출력층 사이의 은닉층인 RNN layer가 하나만 있어도, 첫 번째 시점의 입력은 최종 시점의 출력에 영향을 미친다. 이는 입력 데이터가 최종 출력에 도달하기 전까지 순환 layer를 T번 거치기 때문이다.
■ 이러한 특성 때문에 RNN은 시계열 데이터를 처리하는 데 적합하다. RNN은 시퀀스 데이터의 시간적 의존성과 패턴을 포착할 수 있기 때문이다.
■ 또한, 순환 구조라는 피드백 연결을 통해 정보가 시간 축(time step)을 따라 지속적으로 전달되도록 한다는 점도 크다.
■ 주어진 time step의 입력과 동일한 time step의 출력 사이의 복잡합 관계를 표현하기 위해 RNN layer를 시간 축(time step) 방향뿐만 아니라 입력에서 출력 방향으로도 RNN lyaer를 쌓아 깊은 RNN을 구성할 수 있다.
■ 기본적인 RNN은 시간 축(time step)을 따라 깊이를 가지는 구조라면, 깊은(또는 심층) RNN은 여러 RNN layer를 쌓아 입력-출력 방향으로도 깊이를 확장한다. 이러한 구조를 Stacked RNN 또는 Deep RNN이라고 부른다.
■ 깊은 RNN을 구축하는 일반적인 방법은 다음과 같이 RNN layer들을 서로 위에 쌓는 것이다.
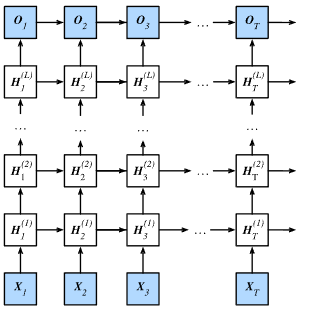
■ 이렇게 쌓은 RNN 셀은 수평 방향(time step 방향), 수직 방향(입력-출력 방향)에 의존한다.
- 예를 들어 H(2)T 셀을 보면, 이전 시점의 같은 레이어의 출력 H(2)T−1과 아래 레이어의 같은 t=T 시점의 출력 H(1)T을 입력으로 받는다.
■ 즉, 자기 자신 레이어의 바로 ① 이전 시점의 레이어와 ② 같은 시점의 바로 아래 레이어에 의존한다.
■ RNN을 여러 층으로 쌓는 논리는 LSTM과 GRU에도 적용할 수 있다.
■ 이렇게 입력-출력 방향으로 은닉층인 RNN layer를 쌓는 접근법은 CNN에서 은닉층을 깊게 쌓아 이미지의 특징을 점진적으로 추출(저수준 패턴 추출부터 추상적 패턴 추출)하는 개념과 일치한다.
■ CNN의 초기 은닉층에서 edge나 blob같은 단순한 특징을 학습하고, 더 깊은 은닉층에서는 추상적인, 복잡한 패턴을 학습하는 것처럼, RNN에서도 레이어를 깊게 쌓음으로써 패턴을 포착할 때 더 복잡한 패턴을 학습할 수 있다.
■ 기본적인 RNN은 학습 과정에서 문장 전체의 맥락에 더 집중하여 토큰(단어, 문자 등)을 시간적 순서에 따라 처리한다면, 깊은 RNN은 입력-출력 방향으로 깊이를 확장함으로써, 문장 전체의 맥락뿐만 아니라 개별 토큰의 특징(ex) 문장 내 단어들의 의미적 관계)에도 집중하는 것으로 볼 수 있다.
■ 단, 이러한 깊은 RNN의 단점은 깊을수록 RNN 셀이 많아지므로 학습 과정(순전파 & 역전파)에서, 많은 항이 포함되어 '깊이 방향'에서 기울기(gradient) 소실/폭발 문제가 발생하기 쉽다는 것이다.
2.2 Deep RNN - Skip Connection
■ 기본적인 RNN은 학습 과정에서 RNN 계층에 기울기를 전파할 때, 기울기 소실/폭발을 억제하고자 LSTM, GRU처럼 게이트(gate)를 추가한 RNN과 기울기 클리핑 방법을 사용한다.
■ 하지만, 깊은 RNN이라면 기울기 소실/폭발이 신경망 계층의 '깊이 방향'에서 발생할 수 있다.
■ 이 깊이 방향에서 발생하는 기울기 문제에 대응하기 위해 스킵 연결(skip connection)을 사용한다.
■ 스킵 연결은 다음과 같이 RNN/LSTM 계층을 건너뛰어 연결하는 단순한 기법이다.
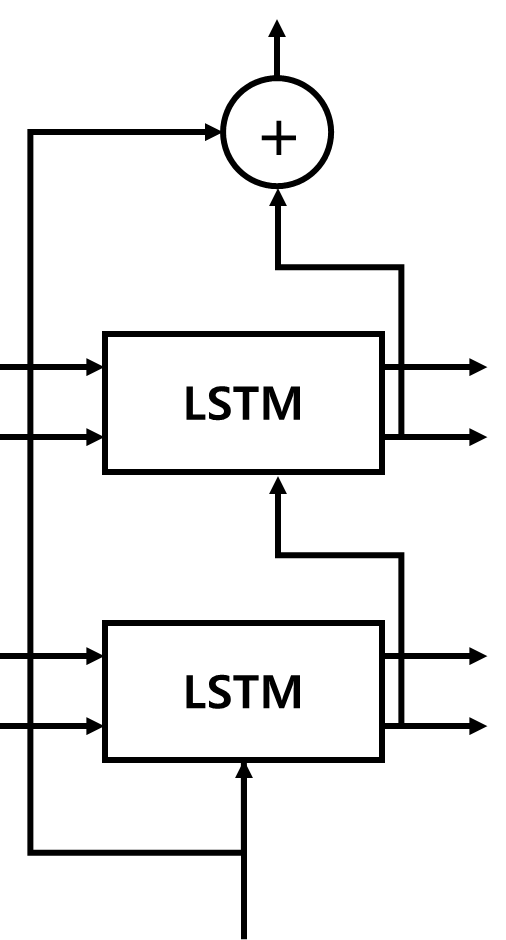
- 위의 예시는 LSTM 계층에 skip 연결을 적용한 것으로, 2개의 출력이 덧셈 노드에서 더해지는 것을 볼 수 있다.
■ 스킵 연결의 핵심은 위와 같은 '덧셈'으로 연결하거나 '연결(concatenation)'을 이용한다.
■ 위와 같이 덧셈 노드로 만든다면, 역전파 과정에서 기울기를 그대로 흘려 보내기 때문에 층이 깊어져도 기울기가 소실되지 않고 전파될 수 있다.
2.3 양방향 순환 신경망(Bidirectional RNN)
■ 예를 들어 'He always drinks black coffee'라는 문장이 있을 때, 기본적인 RNN/LSTM은 시간축이 왼쪽에서 오른쪽으로, 즉 사람이 보통 글을 왼쪽에서 오른쪽으로 읽는 것처럼 동작한다.
■ 이 문장에서 왼쪽 부분을 과거, 오른쪽 부분을 미래라고 생각했을 때, 과거와 미래의 시점에 대한 정보(은닉 상태)를 합치면 과거와 미래 사이에 있는 현재 시점의 예측을 안정적으로 예측할 수 있다.
■ 현재 시점을 t라고 했을 때, 양방향 순환 신경망은 현재 시점 t에서의 출력값을 예측할 때, t 이전 시점의 데이터뿐만 아니라, t 이후 시점의 데이터로도 예측할 수 있다는 아이디어에 기반한다.
■ 왼쪽에서 오른쪽으로(과거 시점에서 미래 시점으로)만 처리하는 모델과 오른쪽에서 왼쪽으로(미래 시점에서 과거 시점으로)만 처리하는 모델을 같이 사용하면 과거 시점의 입력에 있는 정보뿐만 아니라 미래 시점의 입력에 있는 정보를 같이 활용할 수 있으므로 더 좋은 결과가 나오리라 기대할 수 있다.
■ 이렇게 정방향 표현과 역방향 표현을 연결하는 것이 양방향 순환 모델의 목적이다.
- RNN, LSTM, GRU 등 모든 순한 신경망 모델은 양방향으로 구성할 수 있다.
■ 예를 들어 양방향 순환 신경망을 이용해 'He always drinks black coffee' 문장을 인코딩한다면,
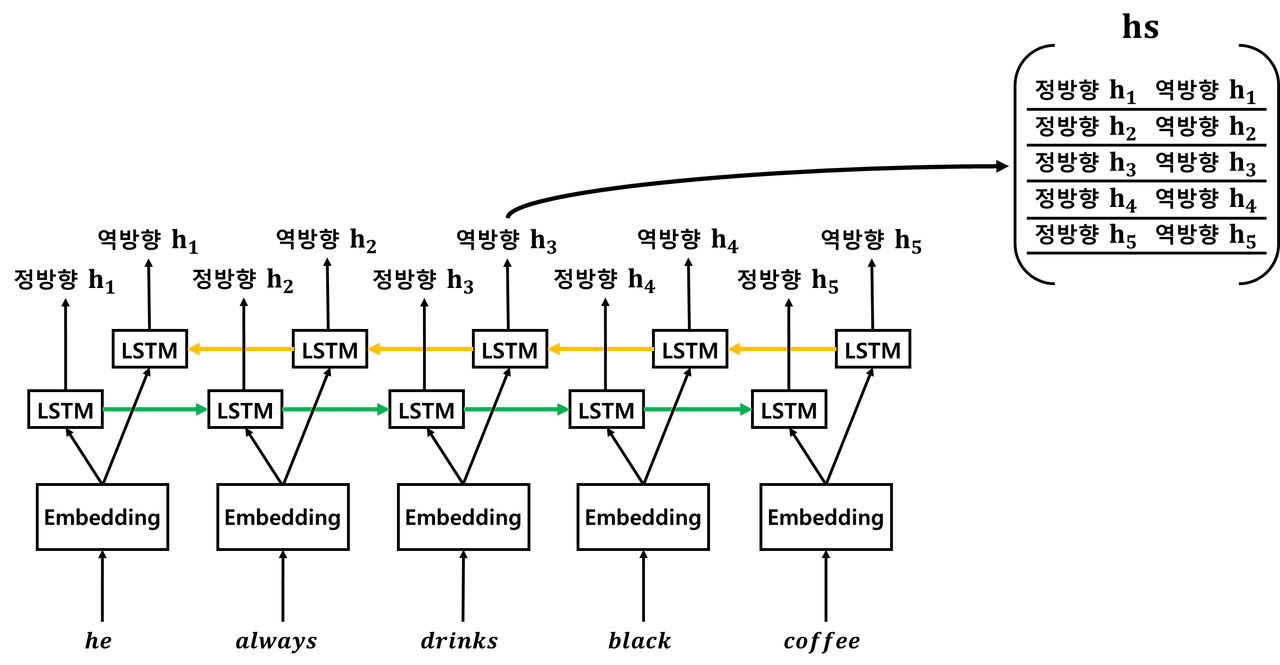
■ 위의 예시처럼 정방향으로 인코딩하는 LSTM과 역방향으로 인코딩하는 LSTM이 추가된다. 양방향은 하나의 출력값을 예측하기 위해 기본적으로 두 개의 메모리 셀을 사용한다.
- 정방향 은닉 상태(forward hidden state)가 앞 시점의 은닉 상태, 역방향 은닉 상태(backward hidden state)가 뒤 시점의 은닉 상태이다.
- 정방향 은닉 상태는 기본적인 순환 신경망처럼 앞 시점의 은닉 상태를 계승 받아(전달받아) 현재의 은닉 상태를 계산한다.
- 역방향 은닉 상태는 뒤 시점의 은닉 상태를 전달받아 현재의 은닉 상태를 계산한다.
- 그리고 정방향 은닉 상태의 값과 역방향 은닉 상태의 값을 통해 출력값을 계산한다.
■ 예를 들어, 현재 시점 t가 t=2일 때, 현재 시점 단어 'always'의 은닉 상태를 계산하기 위해 앞 시점의 은닉 상태와 마지막 시점으로부터의 은닉 상태를 전달받아 현재 시점의 은닉 상태를 계산하는 것을 볼 수 있다.
■ 최종적으로 해당 시점의 정방향 LSTM 계층과 역방향 LSTM 계층에서 계산한 각각의 현재 시점에 대한 은닉 상태를 연결 시킨 벡터를 최종 은닉 상태로 사용한다.
■ 이렇게 양방향으로 정보(은닉 상태)를 처리함으로써, 현재 시점의 은닉 상태 벡터에 과거와 미래의 정보를 압축시킬 수 있다.
- 은닉 상태 벡터는 고정 길이 벡터이다.
- 이 예에서는 앞 시점의 은닉 상태와 뒤 시점의 은닉 상태를 '연결'하는 방식을 사용했지만, '연결' 외에도 더하거나 평균 내는 방법 등 다른 방법도 사용할 수 있다.
■ 양방향 순환 신경망을 구현하는 가장 간단한 방법은 다음과 같다.
- 입력 문장을 왼쪽에서 오른쪽으로 처리하는 정방향 순환 신경망이 문장 'A B C D'를 A, B, C, D 순으로 처리하게 하고
- 반대 방향, 오른쪽에서 왼쪽으로 처리하는 역방향 순환 신경망은 입력 장 단어들의 순서롤 반대로 나열해서 'D C B A' 문장을 D, B, C, A 순으로 처리하게 만든다.
- 마지막으로 두 순환 신경망 계층의 출력(은닉 상태)을 연결하면 양방향 순환 신경망 계층이 완성된다.
■ 그리고 이 예에서는 정방향과 역방향 한 세트, 즉 한 층의 양방향 순환 신경망을 표현했지만, 양방향 순환 신경망도 깊이 방향으로 쌓아 층을 깊게 만들 수 있다.
참고) 합성곱 신경망(CNN) (2)
합성곱 신경망(CNN) (2)
1. 층을 깊게 하는 이유 ■ CNN 훈련이 끝나면 활성화 맵은 다음 그림과 같이 원본 이미지들의 특징들을 추출해서 가지고 있다. 원본 이미지의 특징을 추출해서 가지고 있는 활성화 맵을 피처 맵(f
hyeon-jae.tistory.com
'자연어처리' 카테고리의 다른 글
| LSTM, GRU (1) (0) | 2025.03.28 |
|---|---|
| RNN (2) (0) | 2025.03.26 |
| 시퀀스투시퀀스(Sequence‑to‑Sequence, seq2seq) (1) (0) | 2025.03.19 |
| Subword Tokenizer - (3) Unigram Tokenization (0) | 2025.03.17 |
| Subword Tokenizer - (2) WordPiece Tokenization (0) | 2025.03.16 |



