미분 자동 계산 (2)

1. 미분

1.1 미분이란

Differential equations

1. 미분의 정의1.1 변화율(증분)■ 다음과 같이 종속변수가 $y$ 이고 독립변수가 $x$ 인 $y = f(x)$ 가 있다고 했을 때, 독립변수 $x$ 의 변화량을 $x$ 의 증분이라 하고 델타 기호를 붙여 \( \De

hyeon-jae.tistory.com

■ 어떤 함수 $f(x)$ 가 있을 때, 미분은 보통 $\displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}$ 로 정의한다. 이는 극한으로 짧은 시간(순간)( $\Leftrightarrow \displaystyle\lim_{h \to 0}$ )에서의 변화량이다. 간단히 말하면 '변화율'을 뜻한다.

- 예를 들어, 어떤 물체의 시간에 따른 위치가 있을 때, 위치의 1차 미분(위치의 변화율)은 속도이며, 위치의 2차 미분인 시간에 대한 속도 변화율(미분)은 가속도이다.

■ $\displaystyle\lim_{h \to 0}$ 은 극한을 나타내며, 이때의 $h$ 는 한없이 0에 근접한다는 뜻이다. 그리고 $\dfrac{f(x + h) - f(x)}{h}$ 는 다음과 그림과 같이 두 점을 지나는 직선의 기울기이다.

■ 위의 그림에서 $a$ 를 $x$ 라고 하자. $b - a$ 는 $x$ 가 시간이 지남에 따라 $b - a$ 만큼 변화했을 때의 변화량을 의미하며, 이 변화량을 $x$ 의 증분 $\Delta{x}$ 라고 한다.

[출처] https://koki0702.github.io/dezero-book/en/step04.html

$x$ 축의 변화량 $b - a$ 를 $b - a = h$ 로 둔다면, $a$ 는 $x$ , $b$ 는 $x + h$ 로 나타낼 수 있다.

■ 이때, $x$ 에서의 $y$ 의 값은 $f(x)$ 이며, $x + h$ 에서의 $y$ 의 값은 $f(x + h)$ 가 된다. 즉, $x$ 가 $x+h$ 만큼 변화할 때, $y$ 는 $f(x)$ 에서 $f(x+h)$ 만큼 변화한다. 이때의, $x$ 의 변화량에 따른 $y$ 의 변화량을 증분 $\Delta{y}$ 라고 한다.

- 이때, $y$ 의 변화량은 함숫값인 $f(x)$ 와 $f(x+h)$ 의 차이이며, 이러한 임의의 두 점에서의 함숫값들의 차이에 대한 값을 '차분'이라고 한다.

■ $a = x$ 와 $b = x + h$ 라는 두 점에서 함수 $f(x)$ 의 변화 비율은, $x$ 에 따른 $y = f(x)$ 의 변화 비율이므로 분자를 $x$ 의 변화량, 분모를 $y$ 의 변화량으로 두어 $\dfrac{\Delta{y}}{\Delta{x}}$ 로 표현할 수 있으며, 이는 다시 $\dfrac{f(x+h) - f(x)}{h}$ 로 표현할 수 있다. 이 것을 닫힌 구간 $[x, x+h]$ 에서의 '평균변화율'이라고 부른다.

■ 다시 말해, 평균변화율 $\dfrac{f(x+h) - f(x)}{h}$ 는 함수 $f(x)$ 의 변화 비율이며, 분자가 $x$ 의 증가량, 분모가 $y$ 의 증가량으로 두 점을 지나가는 직선의 기울기이다. 즉, 평균변화율은 '두 점 $x$ 와 $x + h$ 를 잇는 그래프의 기울기이다.

■ 평균변화율 $\dfrac{f(x+h) - f(x)}{h}$ 에서 $x$ 의 증가량(변화율)인 $b - a = h$ 를 순간적으로 한없이 0에 가깝게 줄인다면, 그것은 $x$ 의 변화 비율이며, 그 값이 바로 $y = f(x)$ 의 미분이다.

■ 이때, $y = f(x)$ 일 때, $x = c$ 에서 평균변화율의 극한값이 존재할 때, 함수 $f(x)$ 는 $x= c$ 에서 '미분가능'하다고 표현한다. 이 때는 $x = c$ 에서 '좌 미분계수'와 '우 미분계수'가 동일할 때이다. 그리고 이때의 값을 $x = c$ 에서의 미분값이라고 하며 $f'(c)$ 라고 나타낼 수 있다.

■ 이렇게 "어떤 한 점 $x = c$ 에서 평균변화율의 극한값 $\displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}$ 이 어떤 구간 $[c, c+h]$ 에서 존재할 때, 이 극한값을 $f(x)$ 의 도함수"라고 한다.

■ 정리하면, 도함수 $\displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = f'(x)$ 는 하나의 함수이며, $\displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = f'(x)$ 로 나타낼 수 있다.

■ 그리고 이렇게 $x = c$ 예시처럼 함수 $y = f(x)$ 의 한 점에서 미분계수가 존재한다면, $x= c$ 에서 '미분가능'하다고 표현하는데,

■ $x = c$ 에서 '미분이 가능하다'라는 말은, '미분계수가 존재한다'는 말이고, 미분계수(순간변화율) $\displaystyle\lim_{h \to 0} \dfrac{f(c + h) - f(c)}{h}$ 가 존재한다는 건. 이 극한값이 $\displaystyle\lim_{h \to 0} \dfrac{f(c + h) - f(c)}{h} = f'(c)$ 로 $f'(c)$ 라는 극한값이 존재한다는 것이며, 이 극한값이 존재한다는 것은 다시 좌미분계수와 우미분계수가 같다는 의미가 된다.

■ 좌 미분계수(=좌 기울기)와 우 미분계수(=우 기울기)가 같기 위해서는 함수의 연속을 생각해 본다면, 이는 도함수 $f'(x)$ 가 '연속'이어야 한다. 여기서 말하는 '연속'은 함수가 끊기지 않고 이어져 있음을 의미한다.

- $x = c$ 에서의 미분계수 $f'(c)$ 는 $x$ 축의 점 $c+h$ 가 $c$ 로 한없이 가까워질 때, 그때의 순간변화율로 이는 $f(x)$ 의 그래프 위의 점 $(c, f(c))$ 에서의 '접선의 기울기'와 같다.

- " $f'(c) \Leftrightarrow$ $f(x)$ 의 그래프 위의 점 $(c, f(c))$ 에서의 접선의 기울기"는 $f'(x)$ 라는 도함수에 $x = c$ 라는 점을 넣었을 때, 도함수의 출력값으로 볼 수 있다.

- 즉, 어떤 한 점에서의 접선의 기울기는 그 점에서의 미분계수와 같은 말이다.

■ 즉, "도함수 $f'(x)$ 가 연속이면 미분가능"이라고 할 수 있다.

1.2 수치 미분

■ $f'(x) = \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}$ 를 파이썬에서 완벽하게 구현하기는 어렵다. $h \rightarrow 0$ 은 $h = 0$ 이라는 의미가 아니라, $h$ 가 무한히 0으로 좁히는 것을 의미한다. 이때, $h$ 가 아주 작은 소수점 단위의 값이 되면 파이썬에서는 실수를 근삿값으로 표현하면서 발생하는 부동 소수점 반올림 오차가 발생할 수 있다.

■ 이와 같은 문제를 개선하기 위해 $h$ 의 값을 $h = 0.0001 = 1e-4$ 와 같은 문제가 되지 않을 정도의 값으로 사용해서 $f'(x) = \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}$ 를 계산한다. 이렇게 근사하여 함수의 변화량을 구하는 방법을 수치 미분( numerical differentiation)이라고 한다.

■ 수치 미분은 $h = 0.0001 = 1e-4$ 처럼 작은 값을 사용하여 진짜 미분을 근사하여 구하기 때문에 어쩔 수 없이 값에 오차가 포함된다. 이 오차를 근사 오차라고 한다.

■ 이 근사 오차를 줄이는 방법으로 '중심차분 또는 중앙차분(centered difference)'이라고 부르는 방법이 있다.

■ 중앙차분은 진짜 미분을 구하는 에서 분자에 있는 차분(함수값의 차이)인 $f(x)$ 와 $f(x+h)$ 의 차이를 구하는 대신, 다음과 같이 $f(x-h)$ 와 $f(x+h)$ 의 차이를 계산한다.

중앙차분: $\displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x-h)}{2h} = f'(x)$

- 여기서 점 $x$ 에 대한 미분이 진짜 미분이며, 이때의 $f'(x)$ 는 점 $x$ 에서의 접선으로 초록색 선이다.

- 그리고 빨간색 선은 $x$ 와 $x+h$ 지점에서의 기울기를 구하는 방법으로 '전방차분 또는 전진차분(forward difference)'이라고 부른다.

- 파란색 선이 $x - h$ 와 $x + h$ 에서의 기울기를 구하는 '중앙차분'이다.

■ 위의 그림에서 중앙차분으로 구한 (접선의) 기울기인 파란색 선과 전진차분으로 구한 기울기인 빨간색 선을 비교하면, 진짜 기울기를 나타내는 초록색 선에 가까운 기울기는 중앙차분으로 구한 파란색 선임을 볼 수 있다.

■ 즉, 전진차분보다 중앙차분으로 구한 기울기가 진짜 미분과 더 근사(approximation)하다. 그래서 진정한 미분값에 근사하기 위하여 중앙차분을 사용하는 것이다.

cf) 실제로 중앙차분이 진정한 미분값에 가깝다는 사실은 테일러 급수를 이용해 증명할 수 있다.

■ 중앙차분을 이용하여 수치 미분을 계산하는 함수는 다음과 같이 정의할 수 있다.

def numerical_diff(f, x, eps = 1e-4):
    ## x_0은 x - h, x_1은 x + h에 해당된다.
    x_0, x_1 = Variable(x.data - eps), Variable(x.data + eps)
    y_0, y_1 = f(x_0), f(x_1) 
    c_diff = (y_1.data - y_0.data) / (2 * eps) # 중앙차분에 대한 식
    return c_diff

- 중앙차분을 이용하여 수치 미분을 계산하는 numerical_diff의 세 번째 인수 eps는 아주 작은 값(엡실론)을 의미하는 인수로, 이는 h에 해당된다.

- 이때 h는 앞서 말한 부동 소수점 반올림 오차를 피하기 위해, 문제가 되지 않을 정도의 값인 0.0001을 기본값으로 설정하였다.

- 그리고 첫 번째 인수 f는 미분의 대상이 되는 함수로 다음과 같이 정의한 Function 클래스의 인스턴스이다.

class Function:
    def __call__(self, input):
        x = input.data
        y = self.forward(x) # 사용자가 원하는 연산은 forward 메서드에서 진행된다.
        output = Variable(y)
        return output

    def forward(self, x):
        raise NotImplementedError()

- 두 번째 인수 x는 미분을 계산하는 변수로, 다음과 같이 정의한 Variable 클래스의 인스턴스이다.

class Variable:
    def __init__(self, data):
        self.data = data

■ 예를 들어, 다음과 같이 제곱을 연산하는 함수(= $y = x^2$ )에 대해 수치 미분을 계산한다면

class Square(Function):
    def forward(self, x):
        return x**2

x = Variable(np.array(2.0))
f_square = Square()
dy = numerical_diff(f_square, x)

print(dy)
```#결과#```
4.000000000004
````````````

- 계산 결과를 보면, 수치 미분으로 인해 근사 오차를 포함한 결과 값이 출력되는 것을 확인할 수 있으며, 중앙차분을 이용하여 수치 미분을 계산하였기 때문에 근사 오차의 값이 매우 작음을 볼 수 있다.

- 위의 결과 미분한 값이 4.000...이다. 즉, $x$ 를 2.0에서 아주 작은 값만큼 변화시켜면 $y$ 의 값은 4.000..만큼 변한다는 의미이다.

1.3 수치 미분을 이용한 합성 함수의 미분

■ 다음과 같이 $f(x) = x^4)를 연산하는 함수와 \( g(x) = 2x-1$ 를 연산하는 함수에 대한 클래스를 정의한 다음, 수치 미분을 이용하여 합성 함수 $(g \circ f)(5)$ 를 계산해보자.

class f_x(Function):
    def forward(self, x):
        return x**4

class g_x(Function):
    def forward(self, x):
        return 2*x -1
        
ff = f_x()
g = g_x()

x = Variable(np.array(2.0))

print(g(x).data, ff(x).data)
```#결과#```
3.0 16.0
````````````

## 합성 함수 형태를 사용자 정의 함수(def)로 정의하기

def function_composition(x): # x는 Variable 클래스의 인스턴스
    ## 함수 클래스의 인스턴스 생성
    g = g_x()
    f = f_x()
    return f(g(x))

dy = numerical_diff(function_composition, x)
print(dy)
```#결과#```
216.00000096022143
````````````

- 합성 함수를 function_composition이라는 함수로 정의하였다.

- 파이썬에서 함수도 객체이기 때문에 다른 함수에 인수로 전달할 수 있다.

■ 합성 함수 $y = f(g(x))$ 를 미분하면, 속미분으로 인하여 $y' = f'(g(x)) \cdot g'(x)$ 가 된다.

그러므로 위의 합성함수는 $y = (2x-1)^4$ 이며, 이를 미분하면 $y' = 4(2x-1)^3 \cdot 2$ 가 된다. 여기에 $x = 2$ 를 넣으면 $x = 2$ 에서 $y = f(g(x))$ 의 미분값이며, 그 값은 216이다. 이는 $x = 2$ 에서 아주 작은 값 $h$ 만큼 변화시키면 $y$ 의 값은 216배만큼 변한다는 것을 의미한다.

1.4 수치 미분의 문제점

■ 1.2, 1.3에서 중앙차분을 이용하여 수치 미분을 계산하는 함수를 정의해서 단순한 함수에 대한 미분과 합성 함수에 대한 미분값을 계산했을 때,

■ '4.000000000004', '216.00000096022143'처럼 미분값에 근사 오차 '.000000000004', '.00000096022143'가 포함되는 것을 확인할 수 있었다.

■ 이러한 오차는 대부분의 경우 1.2, 1.3의 예시처럼 매우 작은 값을 가지지만, 어떤 연산이냐에 따라서 오차가 매우 커질 수도 있다.

■ 또한, 수치 미분을 이용하면 변수가 여러 개인 계산을 미분할 경우, 변수 각각을 미분해야 하기 때문에 이런 경우에는 계산량이 많아진다. 그러므로 변수가 수백, 수천만 개 이상인 신경망에서는 손실(loss) 계산을 수치 미분으로 하기에는 무리이다. 그래서 수치 미분이 아닌 '역전파(backpropagation)'를 사용하는 것이다.

2. 역전파(BackPropagation) 이론

■ 파이썬에서 수치 미분을 이용해 미분을 근사하여 계산할 수 있지만, 이 방법은 정확도, 계산 비용에 문제가 있다.

■ 역전파를 이용하면 결과 값의 오차도 더 적게하고 미분 계산을 더 효율적으로 할 수 있다.

■ 이러한 역전파의 근본은 연쇄 법칙(chain rule)에 있다.

2.1 연쇄 법칙(Chain Rule)

■ 연쇄 법칙에 따르면, 여러 개의 함수가 연결된 합성 함수의 미분은, 합성 함수를 구성하는 각각의 함수들을 미분한 후 곱한 것과 같다.

■ 다시 말해, 연쇄 법칙은 합성 함수의 미분에 대한 성질이다.

■ 합성 함수는 두 함수 $f, g$ 가 $f : X \rightarrow Y$ , $f : Y \rightarrow Z$ 로 주어졌을 때 $X$ 의 임의의 원소 $x$ 에 $Z$ 의 원소 $g(f(x))$ 를 대응 시키는 새로운 함수를 $f$ 와 $g$ 의 합성 함수 $(g \circ f)$ 라고 한다.

■ 합성 함수의 미분은 이 합성 함수를 구성하는 각 함수의 미분의 곱으로 마치 사슬로 이어져 있는 것처럼 나타낼 수 있다. 이것이 연쇄 법칙의 원리이다.

■ 함수 $z = f(x, y)$ 에서 $x, y$ 가 각각 변수 $t$ 의 함수일 때, $z$ 는 $t$ 만의 함수라고 볼 수 있다. 따라서 미분 시, 다음과 같이 $z$ 의 $t$ 에 대한 도함수를 생각할 수 있다.

- $z = f(x, y), \quad x = A(t), \quad y = B(t)$ 라고 하면, $z$ 에 대한 $t$ 의 미분 $\dfrac{dt}{dz}$ 는 $\dfrac{dz}{dt} = \dfrac{\partial z}{\partial x} \cdot \dfrac{dx}{dt} + \dfrac{\partial z}{\partial y} \cdot \dfrac{dy}{dt} = f_x \cdot \dfrac{dx}{dt} + f_y \cdot \dfrac{dy}{dt}$ 로 각 함수의 미분의 곱으로 나타낼 수 있다.

- 이는 $\dfrac{dz}{dt}$ (= $z$ 에 대한 $t$ 의 미분), $\dfrac{\partial z}{\partial x}$ (= $x$ 에 대한 $z$ 의 미분)와 $\dfrac{dx}{dt}$ (= $t$ 에 대한 $x$ 의 미분)을 곱한 값에 $\dfrac{\partial z}{\partial y}$ (= $y$ 에 대한 $z$ 의 미분)와 $\dfrac{dy}{dt}$ (= $t$ 에 대한 $y$ 의 미분)을 곱한 값을 더한 것이다.

- 이 연쇄 법칙은 마치 복잡한 계산인 ' $z$ 에 대한 $t$ 의 미분'을 분해하여 단순한 미분 계산으로 구성해서 최종 결과를 계산하는 '국소적 계산'으로 볼 수 있다.

■ 예를 들어, $y = F(x)$ 라는 함수가 있을 때, 이 함수는 $s = A(x), \; t = B(s),\; y = C(t)$ 라는 3개의 함수로 구성되는 합성 함수라고 한다면, 이 합성 함수는 다음과 같은 계산 그래프로 나타낼 수 있다.

■ 이 합성 함수에 대하여 $x$ 에 대한 $y$ 의 미분은 속미분으로 인해, 다음과 같이 각 함수의 미분의 곱으로 마치 사슬로 연결된 것처럼 나타낼 수 있다.

$\dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{ds} \dfrac{ds}{dx}$

- $y = f(g(x))$ 라고 할 때, 속미분으로 인하여 $y' = f'(g(x)) \cdot g'(x)$

■ 이때, $ \dfrac{dy}{dx} = \dfrac{dy}{dt} \dfrac{dt}{ds} \dfrac{ds}{dx} $에서 다음과 같이 $1 = \dfrac{dy}{dy}$ 를 넣어 표현할 수 있다.

$\dfrac{dy}{dx} = \dfrac{dy}{dy} \dfrac{dy}{dt} \dfrac{dt}{ds} \dfrac{ds}{dx}$

2.2 역전파 원리

■ $\dfrac{dy}{dx} = \dfrac{dy}{dy} \dfrac{dy}{dt} \dfrac{dt}{ds} \dfrac{ds}{dx}$ 식은 합성 함수의 미분은 합성 함수를 구성하는 각 구성 함수들의 미분의 곱으로 분해할 수 있음을 의미한다.

■ 이 식은 곱셈으로 이루어져 있으므로 어떤 순서로 곱해도 상관없다. 만약, 출력에서 입력 방향(=역방향) 순서대로 계산한다면 다음과 같이 괄호를 씌울 수 있다.

$\dfrac{dy}{dx} = \left( \left( \dfrac{dy}{dy} \dfrac{dy}{dt} \right) \dfrac{dt}{ds} \right) \dfrac{ds}{dx}$

■ $\dfrac{dy}{dx} = \left( \left( \dfrac{dy}{dy} \dfrac{dy}{dt} \right) \dfrac{dt}{ds} \right) \dfrac{ds}{dx}$ 이 식을 괄호 순서에 맞춰 계산한다면,

- ① $\left( \dfrac{dy}{dy} \dfrac{dy}{dt} \right) = \dfrac{dy}{dt}$

- ② $\left( \left( \dfrac{dy}{dt} \right) \dfrac{dt}{ds} \right) = \dfrac{dy}{ds}$

- ③ $\dfrac{dy}{ds} \dfrac{ds}{dx} = \dfrac{dy}{dx}$

■ 이렇게 ① $\rightarrow$ ② $\rightarrow$ ③ 순서. 즉, 출력(= $y$ ) 방향에서 입력(= $x$ ) 방향으로 곱하면 최종적으로 $\dfrac{dy}{dx}$ 가 계산된다. 이를 계산 그래프로 나타내면 다음과 같다.

■ 위의 그림을 보면, 먼저 $\dfrac{dy}{dy} = 1$ 에서 시작하여 $\dfrac{dy}{dt}$ 와 곱한다. 여기서 $\dfrac{dy}{dt}$ 는 $y = C(t)$ 의 미분이므로 $\dfrac{dy}{dt} = C'(t)$ 로 나타낼 수 있다. 마찬가지로 나머지 도함수에 대해서도 $B'(s), A'(x)$ 로 다음과 같이 나타낼 수 있다.

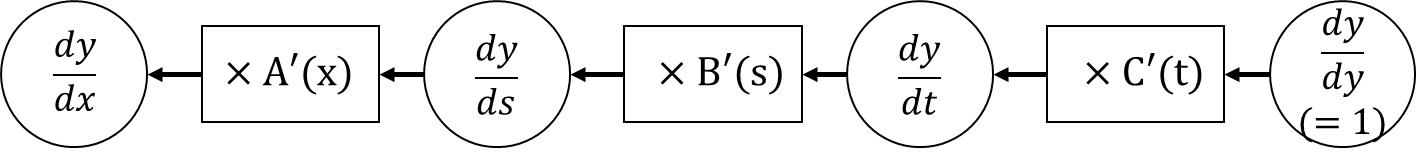
■ 위의 계산그래프를 보면, 변수 $ y, \; t , \; s , \; x $에 대한 미분값이 출력방향에서 입력방향으로 전파되는 것을 볼 수 있다. 이것이 역전파이다. 이때, 중요한 것은 전파되는 값이 모두 $y$ 의 미분값이라는 것이다.

■ 역전파는 이렇게 한 번의 전파만으로 변수의 개수에 상관없이 모든 변수에 대한 미분을 계산할 수 있다.

■ 이 예시에서 사용한 합성 함수의 순전파 계산 그래프와 역전파 계산 그래프를 비교하면, 순전파와 역전파의 관계를 확인할 수 있다.

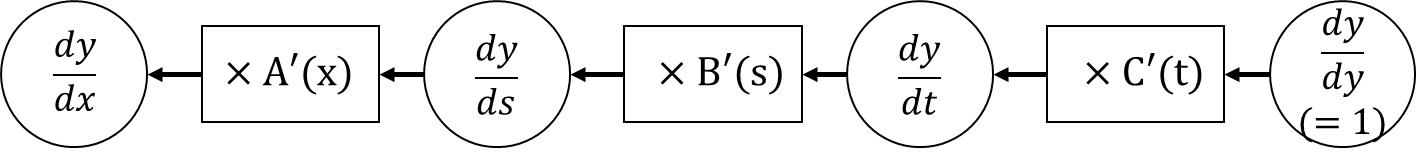
■ 예를 들어, 순전파 과정에서 변수 $s$ 는 역전파 과정에서의 미분 $\dfrac{dy}{ds}$ 에 대응된다. 다른 변수도 마찬가지로 순전파 과정에서 변수 $t$ 는 역전파 과정에서의 미분 $\dfrac{dy}{dt}$ 에, 변수 $x$ 는 $\dfrac{dy}{dx}$ 에 대응된다.

■ 또한, 이러한 대응 관계가 순전파 과정의 함수 $A, \; B, \; C$ 와, 역전파 과정의 함수 $A'(x), \; B'(s), \; C('t)$ 에도 적용된다.

■ 정리하면, 변수는 '통상값'과 '미분값이', 함수는 '통상 계산(순전파)'과 '미분값을 구하기 위한 계산(역전파)'이 존재하는 것으로 볼 수 있다.

■ 역전파를 통해 $\dfrac{dy}{dx}$ 의 값을 계산하기 위해서는 역전파 계산 그래프의 함수 $A'(x), \; B'(s), \; C('t)$ 에 있는 변수 $x, \; s, \; t$ 의 값이 필요하므로, 먼저 순전파를 계산해야 하는 것을 알 수 있다.

'딥러닝' 카테고리의 다른 글

미분 자동 계산 (4) (0)	2025.03.14
미분 자동 계산 (3) (0)	2025.03.13
미분 자동 계산 (1) (0)	2025.03.07
트랜스포머 (Transformer) (3) (0)	2025.01.10
트랜스포머 (Transformer) (2) (0)	2025.01.09

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Hyun_Jae

미분 자동 계산 (2)

1. 미분

1.1 미분이란

1.2 수치 미분

1.3 수치 미분을 이용한 합성 함수의 미분

1.4 수치 미분의 문제점

2. 역전파(BackPropagation) 이론

2.1 연쇄 법칙(Chain Rule)

2.2 역전파 원리

'딥러닝' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

미분 자동 계산 (2)

1. 미분

1.1 미분이란

1.2 수치 미분

1.3 수치 미분을 이용한 합성 함수의 미분

1.4 수치 미분의 문제점

2. 역전파(BackPropagation) 이론

2.1 연쇄 법칙(Chain Rule)

2.2 역전파 원리

'딥러닝' 카테고리의 다른 글

'딥러닝' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역