3.3 트랜스포머 Encoder 내부 구조
3.3.1 Self - Attention
■ 셀프 어텐션의 동작 메커니즘은 먼저, 입력 문장의 단어의 임베딩 벡터들로부터 세 벡터(Q, K, V)를 만들기 위해 가중치 행렬 WQ, WK, WV를 사용한다.
■ 예를 들어 다음과 같이 'Thinking', 'Machines'라는 단어가 입력으로 들어갈 때, 두 단어의 임베딩 벡터가 각각 \( X_1, X_2 \)라면, 임베딩 벡터는 사전에 준비된 가중치 행렬 \( W^Q, W^K, W^V \) 과의 곱을 통해 그에 맞는 Q 벡터, K 벡터, V 벡터를 만들게 된다.
- 단어 'Thinking', 'Machines'의 임베딩 벡터가 가중치 행렬을 통해 각각 Q, K, V 벡터로 변환되는 것을 볼 수 있다.
cf) 위의 과정을 수식으로 나타내면 다음과 같다.
■ 이때, 각 가중치 행렬의 크기는 \( d_{models} \times (d_{models} / num_heads) \)이며, Q, K, V 벡터의 차원은 \( d_{models} \) 값을 \( \text{num_heads} \)로 나눈 값이다.
- 여기서 num_heads는 트랜스포머의 하이퍼파라미터로 병렬 처리 개수이다.
- 논문은 num_heads = 8로 설정하여 Q, K, V 벡터의 차원은 512 / 8 =64이다.
■ 각 단어의 임베딩 벡터로부터 Q, K, V 벡터를 얻었다면, 다음 단계는 문맥 벡터를 구하는 과정으로 어텐션 메커니즘과 동일하다.
어텐션(Attention) (1)
1. 어텐션 구조1.1 seq2seq Encoder 개선■ seq2seq는 다음 예시와 같이 Encoder가 시계열 데이터를 인코딩해서, 인코딩된 정보 \( h \)를 Decoder에 전달한다.■ 이때 \( h \)는 고정 길이 벡터라서 입력 문장이
hyeon-jae.tistory.com
■ Q 벡터와 모든 K 벡터에 대해 내적 연산 \( Q K^T \)을 수행해서 어텐션 스코어를 계산하여, 어텐션 스코어에 Softmax 함수를 적용해서 어텐션 분포를 계산한다.
■ 그다음, 어텐션 분포를 이용해서 모든 V 벡터의 가중합을 계산한다. 이 계산에 대한 결과가 문맥 벡터이다.
■ 이 일련의 과정을 모든 Q 벡터에 대해 반복한다.
■ 단 , 논문에서는 어텐 스코어를 계산하는 과정에 벡터 차원 수의 제곱근인 루트 d_k를 나누어 스케일링을 해었다. \( \text{attention score} = \dfrac{QK^T}{\sqrt{d_k}} \), \( \sqrt{d_k} \)는 Q, K 벡터의 차원이므로 \( d_{models} \) 값을 \( \text{num_heads} \)로 나눈 값이다.
■ 이를 dot production에서 값을 스케일링하는 것을 추가하였다고 하여 스케일된 내적 어텐션(Scaled dot product Attention)이라고 부른다.
■ 스케일링을 하는 이유는 \( d_k \) 값이 작을 때 기본 메커니즘(닷-프로덕트 어텐션(dot-product attention))과 스케일된 내적 어텐션(Scaled dot product Attention)은 유사한 성능을 보이지만, \( d_k \) 값이 클 경우 더 우수한 성능을 낸다.
■ 단, \( d_k \) 값이 클 때, 소프트맥스 함수가 극히 작은 그래디언트를 가지는 영역으로 밀려난다고 추측하여, 이를 방지하기 위해 내적 값을 \( \sqrt{d_k} \)로 스케일링한다.
■ 다음 그림은
- (1) 스케일드 닷 프로덕트 어텐션을 통해 어텐션 스코어를 계산하고,
- (2) 어텐션 스코어에 소프트맥스 함수를 적용해 각 단어의 중요도를 나타내는 어텐션 가중치 얻은 다음,
- (3) 어텐션 가중치를 V 벡터에 적용하고, 가중합을 통해 최종 출력 벡터인 문맥 벡터를 얻는 셀프 어텐션 계층의 과정을 나타낸 것이다

- 이 예시는 첫 번째 단어 'Thinking'에 대한 결과이므로 Softmax의 0.88과 0.12는 단어 'Thinking'은 자기 자신과의 88%만큼의 관계를, 단어 'Machine'과 'Thinking'은 12%만큼의 관계를 맺고 있는 것으로 볼 수 있다.
- 여기서 가중합 결과 \( z \)가 최종 출력 벡터인 문맥 벡터이다.
■ 앞서 설명한 것처럼 이 일련의 과정을 모든 Q 벡터에 대해 반복해야 한다. 이 예시에서는 Q 벡터가 2개이지만, 입력 문장이 길어지면 이러한 벡터 연산 과정을 모두 반복하기에는 시간이 오래 소요된다.
■ 그러므로 실제 계산은 다음 그림처럼 행렬을 사용하여 일괄 계산한다.
■ 아래의 그림은 단어의 임베딩 벡터마다 일일히 가중치 행렬을 곱하지 않고, 단어의 임베딩 벡터로 이뤄진 행렬 \( X \)에 행렬에 가중치 행렬 \( W^Q, W^K, W^V \)를 곱하여 Q 행렬, K 행렬, V 행렬을 만드는 과정이다.

■ Q, K, V 행렬을 모두 구했으면, 이제 어텐션 스코어를 계산해야 한다.
■ 행렬 연산이기 때문에 어텐션 스코어는 \( QK^T \)로 구할 수 있다. \( QK^T \)는 각각의 단어의 Q 벡터와 K 벡터의 내적이 각 행렬의 원소가 되는 행렬이 된다.

■ 그다음, \( QK^T \)에 \( \sqrt{d_k} \)를 나눠주면 각 행과 열이 어텐션 스코어 값을 가지는 행렬이 된다.
■ 예를 들어 위의 2 x 2 행렬에서 thinking 행과 Machine 열의 값은 thinking의 Q 벡터와 cat의 K벡터의 어텐션 스코어이다.
■ 다음으로 어텐션 가중치를 계산하기 위해 다음과 같이 \( \dfrac{QK^T}{\sqrt{d_k}} \)에 소프트맥스 함수를 적용하면 된다.

■ 최종적으로 구해야 할 것은 문맥 벡터들로 이뤄진 문맥 행렬이다. 그러므로 뒤에 V 행렬을 곱해준다.

■ 이렇게 되면 이 문맥 행렬은 모든 단어에 대한 문맥 벡터로 구성된다.
■ 위의 예시에서 사용된 행렬의 크기를 정리하면, 입력 문장의 길이를 \( len \)이라 할 때, 이 예시는 len = 2이다. 그리고 임베딩 벡터의 차원은 \( d_{model} \)이므로 임베딩 벡터로 이뤄진 행렬의 크기는 \( (len, d_{model}) \)이다.
■ 그리고 Q, K, V 행렬의 크기는 Q, K 벡터의 차원을 \( d_k \), V 벡터의 차원을 \( d_v \)라고 하면, Q, K 행렬의 크기는 \( (len, d_k) \), V 행렬의 크기는 \( (len, d_v) \)가 된다.
■ 그렇다면 \( W^Q, W^K, W^V \) 행렬의 크기는 각각 \( (d_{model}, d_k) \), \( (d_{model}, d_k) \), \( (d_{model}, d_v) \)임을 알 수 있다.
■ 마지막으로 문맥 벡터로 구성된 문맥 행렬의 크기는\( QK^T \) \( (len, d_k) \times (d_k, len) = (len, len) \)에 V 행렬을 곱하는 것이므로 \( (len, len) \times (len, d_v) = (len, d_v) \)가 된다.
- 단, 논문에서 Q, K, V 벡터의 차원은 모두 \( (d_{model} / num_heads) \)이다.
■ 여기까지가 셀프 어텐션 계층 내에서 진행되는 과정이다.
3.3.2 Multi-Head Attention
■ 논문에 따르면, \( d_{model} \) 차원의 Q, K, V로 한 번의 셀프 어텐션을 수행하는 대신, Q, K, V를 각각 \( h \)번 선형 투영하여 \( d_k, d_k \) 그리고 \( d_v \) 차원으로 변환하고, 이렇게 투영된 Q, K, V에 대해 병렬로 셀프 어텐션을 병렬 처리하는 것이 더 유용하다는 것을 발견했다.
- 여기서의 \( h \)는 트랜스포머의 하이퍼파라미터 \( num_heads \)
■ 투영된 Q, K, V에 대해 병렬로 어텐션 함수를 수행하여 \( d_v \) 차원의 출력값을 생성한다. 그리고 \( h \) 번 수행된 출력값들을 이어서 다음 그림처럼 최종 값을 생성한다.

■ 이를 식으로 나타내면 다음과 같다.

■ 이때 사용된 가중치 행렬은 다음과 같다.

■ 이 과정의 구체적인 과정은 다음과 같다.
■ \( d_{model} \)의 차원을 \( h = num_heads \)개로 나누어 \( d_{model} / num_heads \) 차원을 가지는 Q, K, V에 대해 \( num_heads \)개의 병렬 셀프 어텐션을 수행한다.
■ 논문에서 사용한 \( h = num_heads = 8(=512/64) \)이다. 즉, 총 8번의 셀프 어텐션을 병렬로 실행한다.
- 이때 \( d_k = d_v = \frac{d_{\text{model}}}{h} = 64 \)를 사용했다. \( d_{model} = 512 \)
- 각 헤드의 차원이 줄어들었기 때문에 결국 전체 차원을 사용하는 단일 헤드 어텐션과 총 계산 비용이 비슷하다.
■ 8번의 셀프 어텐션을 수행했기 때문에, 8개의 문맥 행렬 \( z_0, z_1, \cdots, z_7 \)이 출력된다.
- 이때 각각의 문맥 행렬을 어텐션 헤드(attention head)라고 부른다.
- 이 과정에서 사용된 가중치 행렬 \( W^Q, W^K, W^V \)은 다음과 같으며 8개의 어텐션 헤드마다 전부 다른 값을 가진다.

■ 그다음, 병렬 처리로 나온 각각의 문맥 행렬을 연결(concat)한다. 그리고 여기에 또 다른 가중치 행렬 \( W^o \)와의 내적을 통해 Multi-Head Attention의 최종 결과인 \( Z \)를 얻는다.

- \( \text{MultiHead}(Q, K, V \)가 최종 결과인 \( Z \) 행렬
■ 이때, 모두 연결된 어텐션 헤드 \( Z \) 행렬의 크기는 \( (len, d_{model} \)로, 단어의 임베딩 벡터로 이뤄진 행렬 \( X \)와 동일하다.
■ 여기까지의 과정을 그림으로 나타내면 다음과 같다.

■ 이렇게 병렬로 셀프 어텐션을 수행하여 얻을 수 있는 효과는 바로 셀프 어텐션(여기서는 어텐션 헤드)이 여러 개이기 때문에, 다른 시각으로 하나의 단어가 다른 단어들과 어떻게 관련되는지 알 수 있다는 것이다.
■ 예를 들어 'The animal didn't cross the street because it was too tired' 예에서 쿼리(Q)가 단어 'it'일 때,
- 'it'에 대한 Q 벡터로부터 다른 단어와의 연관도를 구했을 때, 첫 번째 어텐션 헤드가 'it'과 'animal'의 연관도를 높게 측정했다면,
- 두 번째 어텐션 헤드는 '그러면 'it'과 'tired'의 연관도가 높구나'라고 측정할 수 있다.
■ 이 파트에서 중요한 부분은 병렬 처리도 맞지만, 이 과정의 최종 산출물의 크기 \( (len, d_{model} \)이다.
■ 입력으로 들어오는 행렬의 크기가 \( (len, d_{model} \)이기 때문에, 이는 Encoder의 첫 번째 서브 계층인 Multi-Head Attention이 끝났을 때, 입력 행렬과의 크기가 유지되고 있다는 것이다.
■ 그다음 계층인 두 번째 서브 계층인 피드 포워드 신경망을 지날 때 이 크기가 유지되어야 한다. 왜냐하면, 트랜스포머는 동일한 구조의 Encoder를 쌓은 것이기 때문에 입력 크기와 출력 크기가 계속 유지되어야만 다음 인코더 층에 다시 입력될 수 있다.
3.3.3 Residual Block
■ 트랜스포머의 구조를 보면, 피드포워드 계층으로 가기 전에 잔차 블럭(스킵 연결)과 레이어 정규화 계층을 거치는 것을 볼 수 있다.
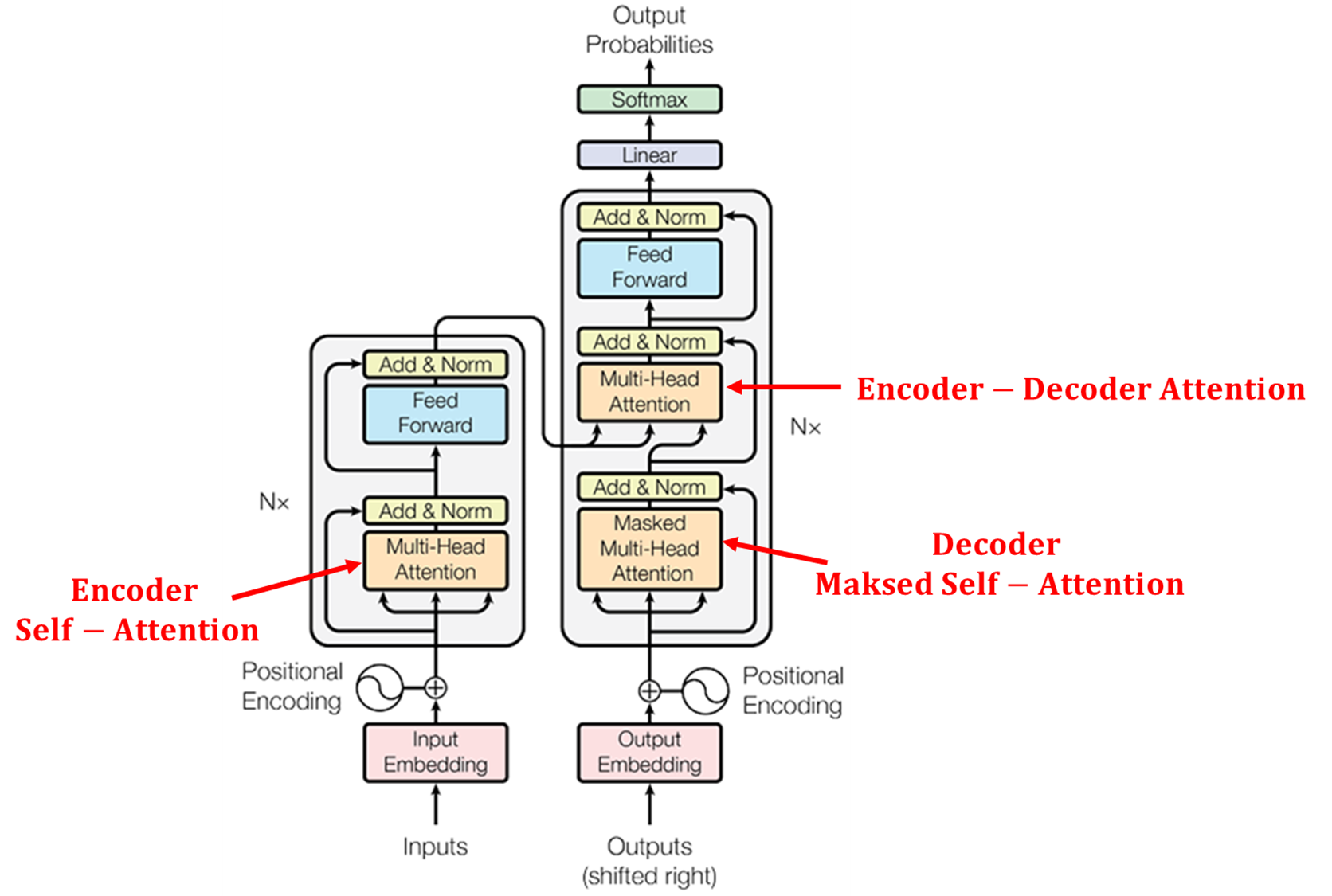
■ 잔차 블록은 다음과 같이 입력 \( x \), 함수 \( F(x) \)와 스킵 연결로 구성되어 있으며, \( H(x) = x + F(x) \)이다.

■ 트랜스포머에서는 \( F(x) \)가 바로 서브 계층이다. 즉, 트랜스포머에서 잔차 블록은 서브 계층의 입력과 출력을 더하는 것으로, 트랜스포머에서 서브 계층의 입력과 출력은 동일한 차원을 가지므로 덧셈 연산을 할 수 있다.
■ 이를 식으로 표현한 것이 논문 3.1 Encoder 부분에 명시된 \( x + Sublayer(x) \)이다.
■ 여기서 중요한 부분은, 위의 트랜스포머 구조를 보면 서브 계층은 Multi-Head Attention이므로 잔차 연결 결과는 \( H(x) = x + \text{Multi-Head Attention} \)이 된다는 것이다.
■ 이때의 \( x \)는 서브 계층의 입력이기 때문에 \( H(x) \)는 Multi-Head Attention의 입력과 Multi-Head Attention의 출력을 더한 값이 된다.
3.3.4 Layer Normalization
■ 잔차 연결을 한 다음 단계는, 논문에 명시된 식 \( \text{LayerNorm}(x + \text{Sublayer}(x) \)처럼 층 정규화 과정이다.
■ Multi-Head Attention의 출력값은 행렬이며, Multi-Head Attention의 입출력 크기는 \( (len, d_{model} \)로 동일하기 때문에, 잔차 연결 결과는 Multi-Head Attention의 입출력 행렬 크기와 동일한 크기를 가지는 행렬이 된다.
■ 그러므로 이 행렬에 대해 층 정규화를 진행해야 한다. 층 정규화 과정은 다음과 같다.
■ 층 정규화는 텐서의 마지막 차원에 대한 평균과 분산을 기반으로 값을 정규화한다. 트랜스포머에서 잔차 연결 결과의 마지막 차원은 \( d_{model} \)이므로 텐서의 마지막 차원은 \( d_{model} \) 차원을 의미한다.
■ 층 정규화를 위해 평균과 분산을 구하는 방법은 \( d_{model \) 차원의 방향으로 각각 평균과 분산을 구한 다음, 이 평균과 분산을 정규화 식에 넣으면 된다.
- 감마와 베타를 이용한 정규화도 가능하다.
참고) https://hyeon-jae.tistory.com/54
매개변수 갱신 방법(2)
1. 가중치 초깃값■ 너무 큰 가중치 (매개변수)값은 학습 과정에서 과적합을 발생시킬 수 있어서 초깃값을 최대한 작은 값에서 시작하거나 가중치 감소 기법을 통해 과적합을 억제해야 한다.■
hyeon-jae.tistory.com
■ 다음 그림은 Residual Block과 Layer Normalization을 거쳐 피드포워드 계층에 들어가는 과정을 나타낸 것이다.
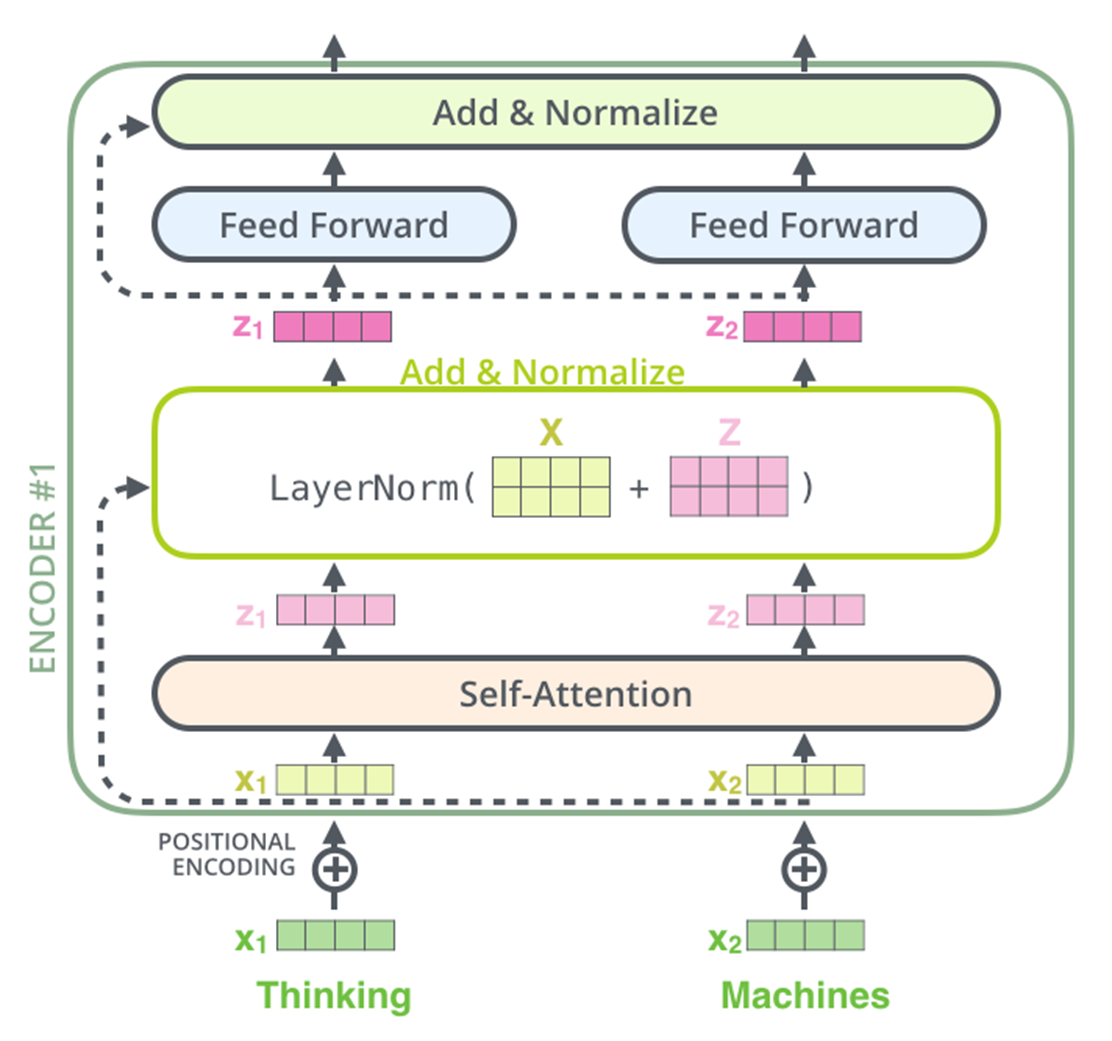
- 잔차 블록에서 Multi-Head Attention의 입력과 Multi-Head Attention의 출력을 더한 값이 더해지는 것을 볼 수 있다.
3.3.5 포지션-와이즈 피드 포워드 신경망(Position-wise Feed-Forward Networks, Position-wise FFNN)
■ FFNN(Feed forward neural network)은 Encoder와 Decoder에서 모두 사용하는 서브 계층이다.
■ 이 네트워크는 다음과 같이 ReLU 활성화 함수를 포함한 두 개의 선형 변환으로 구성된다.
■ 이 식의 과정. 즉, FFNN의 내부 과정을 입력층, 은닉층, 출력층 순서대로 나타내면 다음과 같다.

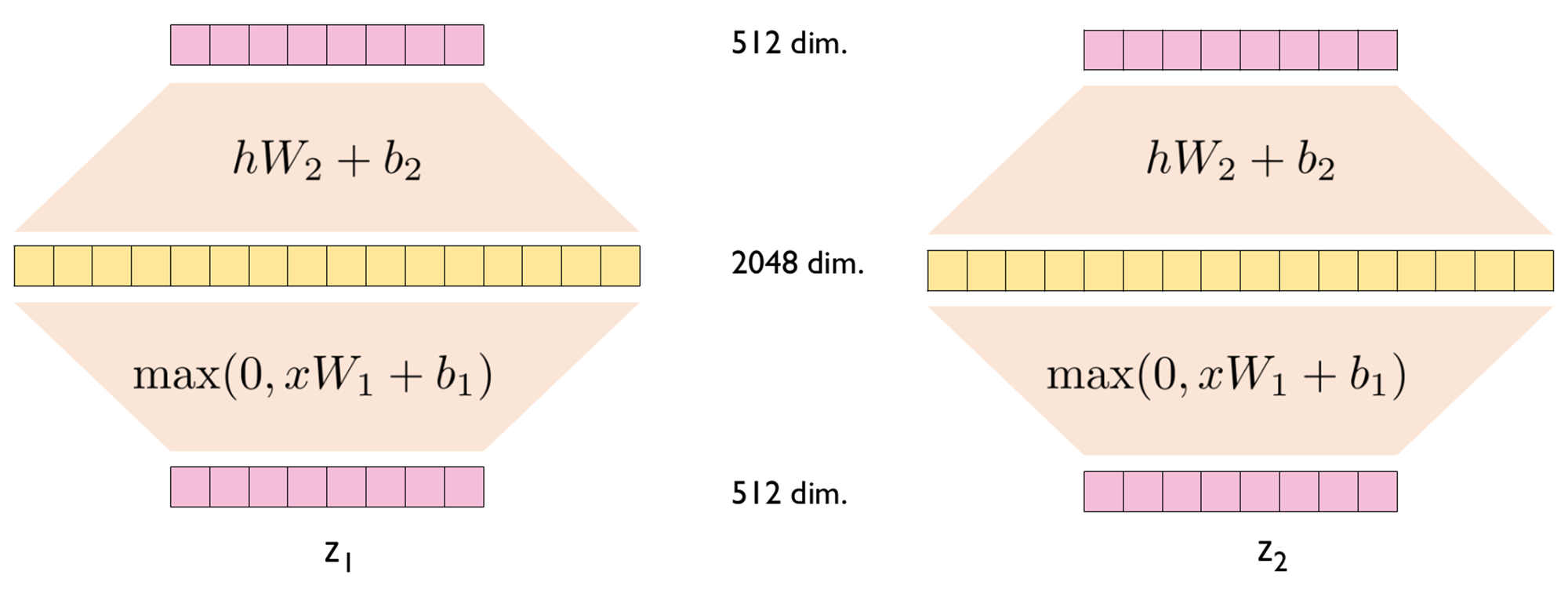
■ 가중치 매개변수 \( W_1, W_2, b_1, b_2 \)는 동일한 인코더 층 내에서는 동일한 값이 사용된다.(동일한 가중치를 공유한다.) 단, 인코더 층마다 다른 값을 가진다.
■ 먼저 입력 \( x \)는 Multi-Head Attention의 결과로 나온 \( (len, d_{model} \)크기를 가지는 행렬이다.
■ \( W_1 \)의 크기는 \( d_{model}, d_{ff} \), \( W_2 \)의 크기는 \( d_{ff}, d_{model} \)이다. 그러므로 FFNN을 통과해도 행렬의 크기는 \( (len, d_{model} \)으로 유지된다.
- \( d_ff \)는 트랜스포머의 하이퍼파라미터로 피드포워드 신경망 은닉층의 크기이다. 논문에서는 \( d_{ff} = 2048 \)로 설정했다.
■ 여기까지가 하나의 인코더 층에서 이뤄지는 과정이다. 이러한 인코더 층을 num_layers개만큼 쌓으면 된다. 그리고 num_layers만큼의 연산을 순차적으로 한 뒤, 마지막 층의 출력을 Decoder에 전달한다.
- Decoder도 num_layers만큼의 연산을 수행한다.
'딥러닝' 카테고리의 다른 글
| 미분 자동 계산 (1) (0) | 2025.03.07 |
|---|---|
| 트랜스포머 (Transformer) (3) (0) | 2025.01.10 |
| 트랜스포머 (Transformer) (1) (0) | 2025.01.09 |
| 어텐션(Attention) (1) (0) | 2025.01.08 |
| 시퀀스 투 시퀀스(Sequence toSequence, seq2seq) (0) | 2025.01.07 |





