1. 미분의 정의
1.1 변화율(증분)
■ 다음과 같이 종속변수가 \( y \)이고 독립변수가 \( x \)인 \( y = f(x) \)가 있다고 했을 때, 독립변수 \( x \)의 변화량을 \( x \)의 증분이라 하고 델타 기호를 붙여 \( \Delta x \)로 나타낸다. 그리고 독립변수 \( x \)의 변화량에 따른 종속변수 \( y \)의 변화량을 \( y \)의 증분이라 하고 \( \Delta y \)로 나타낸다.

■ 예를 들어 \( y = f(x) = x^2 \)이라고 할 때, 독립변수 \( x \)의 값이 1에서 3으로 변한다고 하면 \( x \)의 변화량은 2이다. 이 변화량이 \( x \)의 증분 \( \Delta x \)이다.
그리고 \( x \)가 1에서 3으로 변하면 \( y \)의 값은 1에서 9가 된다. 즉, 독립변수가 2만큼 변화했을 때, 종속변수인 \( y \)의 변화량을 8이며, 이 8은 \( \Delta x \)에 대한 \( y \)의 증분인 \( \Delta y \)이다.
1.2 평균변화율과 순간변화율(=미분계수)
■ 함수 \( f(x) \)에서 \( x \)의 값이 \( a \)에서 \( a + \Delta x \)까지 변할 때, 즉 \( x \)가 어떤 값 \( a \)에서 \( \Delta x \)만큼 변화를 할 때, \( y \)가 \( \Delta y \)만큼 변화한다고 하면, 이 변화량의 비율인 \( \dfrac{\Delta y}{\Delta x} \)를 닫힌 구간 \( [a, \; a + \Delta x] \)에서의 평균변화율이라고 한다.
■ 평균변화율인 \( \dfrac{\Delta y}{\Delta x} \)는 분자가 \( x \)의 증가량, 분모가 \( y \)의 증가량으로 두 점을 지나가는 직선의 기울기이다. 즉, 평균변화율은 '두 점을 잇는(두 점 사이에 있는) 그래프의 기울기'이다.
■ 그리고 분자가 \( x \)의 증가량, 분모가 \( y \)의 증가량이므로 \( x \)가 변했을 때, \( y \)의 변화량을 나타내는 비율로 생각할 수 있다.
■ \( y = f(x) \)에서의 평균변화율을 수식으로 나타내면 \( \dfrac{\Delta y}{\Delta x} = \dfrac{f(a + \Delta x) - f(a)}{\left( a + \Delta x \right) - a} = \dfrac{f(a + \Delta x) - f(a)}{\Delta x} \)이다.
■ 그러므로, 평균변화율을 다음과 같이 정의할 수 있다.
함수 \( y = f(x) \)에서 \( x \)의 값이 \( a \)에서 \( a + \Delta x \)까지 변할 때, \( \dfrac{\Delta y}{\Delta x} = \dfrac{f(a + \Delta x) - f(a)}{\Delta x} \)를 닫힌 구간 \( [a, \; a + \Delta x] \)에서의 \( y \)의 평균변화율이라고 한다.
- 위의 \( y = x^2 \)의 예에서 닫힌 구간 [1, 3]에서 \( x \)의 증분은 2, \( y \)의 증분은 8이므로 \( \dfrac{\Delta y}{\Delta x} = 4 \)가 된다.
- 그러므로 닫힌 구간 [1, 3]에서 \( y \)의 평균변화율은 4라고 할 수 있으며, 이 평균변화율 4는 다음과 같이 \( y = x^2 \)위의 두 점 (1, 1)과 (3, 9)를 지나는 직선의 기울기이다.

■ 여기서 \( x \)의 증분이 한없이 0에 가까워질 때. 즉, \( \Delta x \rightarrow 0 \)일 때 평균변화율 \( \dfrac{\Delta y}{\Delta x} \)가 유한확정인 극한값을 가지면, 이를 함수 \( f(x) \)의 \( x = a \)에서의 (순간)변화율 또는 미분계수라고 한다.
■ \( \displaystyle\lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} = \displaystyle\lim_{\Delta x \to 0} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} \)에서 평균변화율이 극한값을 갖는다는 것은, 평균변화율의 좌극한(=좌미분계수) \( \displaystyle\lim_{\Delta x \to 0^-} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} \)과 우극한(=우미분계수) \( \displaystyle \lim_{\Delta x \to 0^+} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} \)이 다음과 같이 \( x = a \)에서 만나 극한값을 갖는다는 것이다.
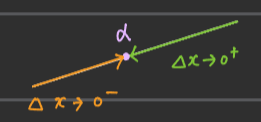
\( \displaystyle\lim_{\Delta x \to 0^-} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} = \displaystyle\lim_{\Delta x \to 0^+} \dfrac{f(a + \Delta x) - f(a)}{\Delta x} = \alpha \), 여기서 \( \alpha \)는 극한값
■ 순간변화율을 구하기 위해 \( \Delta x \rightarrow 0 \). 즉 \( x \)의 증분을 아주 작게 하였다. 그러므로 이때의 변화율은 아주 순간의 변화율이므로 순간변화율이라고 하는 것이다. 그러므로 \( 즉, 순간변화율(=미분계수)의 의미는 \( x \)의 증분을 아주 작게 하였을 때, \( x \)의 증분을 아주 작게 쪼갰을 때의 변화율이므로 그 점에서의 접선의 기울기와 같다.
cf) 평균변화율의 극한값은
- \( x \)값의 변화량(증분)을 \( \Delta x \)로 표현하면 \( \displaystyle\lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} \)
- \( x \)값의 변화량 \( \Delta x \)를 \( h \)로 표현하면 \( \displaystyle\lim_{h \to 0} \dfrac{f(a + h) - f(a)}{h} \)
- \( x \)값의 변화량을 \( b - a \)로 표현하면 \( \displaystyle\lim_{b \to a} \dfrac{f(b) - f(a)}{b-a} \)로 표현할 수 있다.
■ 이렇게 \( x = a \)에서 평균변화율의 극한값이 존재할 때, 함수 \( f(x) \)는 \( x = a \)에서 미분가능(Differentiable)하다고 표현한다.
즉, 미분계수는 연속적인 그래프에서 존재한다. 그래프가 중간에 끊어져 있다면(불연속적이면) 평균변화율의 좌극한과 우극한 값이 달라 에서 평균변화율이 극한값을 가질 수 없다. 그러므로 미분가능하려면 연속적인 그래프여야 한다.
그러므로 함수 \( f(x) \)가 \( x = a \)에서 미분가능하면 \( f(x) \)는 \( x = a \)에서 연속이다.라고 할 수 있다. 단, 역은 성립하지 않는다.
cf) 평균변화율의 극한값. 즉, 순간변화율(=미분계수)는
- \( x \)값의 변화량(증분)을 \( \Delta x \)로 표현하면 \( \displaystyle\lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} \)
- \( x \)값의 변화량 \( \Delta x \)를 \( h \)로 표현하면 \( \displaystyle\lim_{h \to 0} \dfrac{f(a + h) - f(a)}{h} \)
- \( x \)값의 변화량을 \( b - a \)로 표현하면 \( \displaystyle\lim_{b \to a} \dfrac{f(b) - f(a)}{b-a} \)로 표현할 수 있다.
1.3 도함수
■ 그리고 함수 \( y = f(x) \)의 각 점마다 미분계수가 존재한다면, \( \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)로 나타낼 수 있으며, \( \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)은 하나의 함수로 생각할 수 있다.
■ 이렇게 미분의 정의로부터 만들어진 함수 \( \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} \)를 도함수라고 부르며 \( f'(x) \)로 나타낸다. \( \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = f'(x) \)
- 즉, \( \displaystyle\lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h} = f'(x) \)이 도함수의 정의이다.
■ 이 도함수 \( f'(x) \)를 구하는 과정을 미분한다라고 표현한다. 이때 \( f'(x) \)는 한 번 미분을 한 것이므로 '1계 도함수' 또는 '1계 미분'이라고 부른다.
- 1계 도함수를 한 번 더 미분한 함수를 '2계 도함수'라고 부르고, \( n \)번 미분하면 '\( n \)계 도함수'라고 부른다.
- 2계 도함수 이상부터 \( n \)계 도함수를 통틀어 '고계도함수'라고 부른다.
참고) \( f'(x) \)를 뉴턴이 사용한 \( y' \)이나 라이프니츠가 사용한 \( \dfrac{dy}{dx} \)로 표기할 수 있다.
■ 이렇게 미분은 연속적으로 변화하는 함수의 변화율을 구한다고 볼 수 있다.
2.미분방정식(Differential equation)과 지수 함수(Exponential function)의 관계
■ 미분방정식은 미지의 함수와 그 도함수 그리고 이 함수들의 함수값에 관계된 여러 개의 변수들에 대한 함수 방정식이다. 이 미분방정식에는 하나 또는 그 이상의 독립변수에 관하여 하나 또는 그 이상의 종속변수의 도함수가 포함되어 있다. 일반적인 방정식이 미지수(독립변수) \( x \)의 값을 구하는 것과 달리, 미분방정식은 미지'함수'를 구하는 것이 목적이다.
- 하나의 독립변수인 \( dx \)만을 가지는 형태의 식을 상미분방정식(ordinary differential equation)이라고 하며, 일반적인 미분방정식이다.
- 여러 개의 독립변수를 가지는 형태를 편미분방정식(partial differential equation)이라고 하며, 종속 변수를 서로 다른 독립변수로 미분한다. 이것을 기호로 나타내기 위해 delta를 의미하는 \( d \) 대신, round 기호 \( \partial \)을 이용하여 표기한다.
- \( \dfrac{d^2 y}{dx^2} + \frac{d y}{dx} - y = -2x \)같은 형태가 미분방정식, \( \dfrac{\partial^2 u}{\partial y^2} + \dfrac{\partial^2 u}{\partial x^2} = 0 \)같은 형태가 편미분방정식
■ 미분방정식은 지수함수가 포함된 일반해의 형태로 표현할 수 있으며, 지수함수가 포함된 일반해의 형태를 통해 미분방정식의 해(solution)를 구할 수 있다.
■ 예를 들어 \( \dfrac{dy}{dx} \)는 \( x \)의 변화에 대한 \( y \)의 변화율. 즉, \( y \)를 \( x \)로 미분한 것이다. \( y \)의 변화율(미분값)은 \( y \)와 비례하므로, 이 미분의 결과 값은 \( y \)의 값에 어떤 상수 \( k \)를 곱한 것으로 나타낼 수 있다. \( \dfrac{dy}{dx} = ky \)
■ \( \dfrac{dy}{dx} = ky \)의 식에서 좌변을 \( y \)에 대한 식으로 만든 다음, 양변에 대해 적분을 취하면 미지함수인 \( y \)에 대한 일반해가 지수함수가 포함된 형태로 나타나는 것을 확인할 수 있다.

■ 이렇게 미분방정식의 일반해를 도출할 수 있으며, 이때의 일반해는 지수함수 형태임을 확인할 수 있으며,
■ 독립변수인 \( x \)의 값을 안다면, 미분방정식의 일반해 \( y = C \cdot e^{kx} \)를 통해 미분방정식의 해(solution)를 구할 수 있다.
3. Systems of Differential equation
■ 예를 들어, 두 개의 선형미분방정식이 \( \dfrac{du_1}{dt} = - u_1 + 2u_2, \dfrac{du_2}{dt} = - u_1 - 2u_2 \)으로 있다고 하면,
■ 두 선형미분방정식에는 각각 서로를 포함( \( u_1 \)에 대한 미분방정식에는 \( u_2 \)가, \( u_2 \)에 대한 미분방정식에는 \( u_1 \)이 포함되어 있음)하고 있기 때문에 \( u_1 \)과 \( u_2 \)는 서로 관계가 있다고 볼 수 있다.
■ \( u_1, u_2 \)를 하나의 벡터로 만들어서 두 미분방정식을 행렬과 벡터의 곱 형태로 만들 수 있다. 그 방법은 \( \dfrac{du}{dt} = Au \)로 두는 것이다.
- 이때, 행렬 \( A \) 옆에 있는 \( u \)는 \( u(t) = \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} \)로 정의한다면,
- 좌변에 있는 \( \dfrac{du}{dt} \)는 \( u \)를 미분한 것이므로 \( u'(t) = \begin{bmatrix} u'_1 \\ u'_2 \end{bmatrix} \)로 정의할 수 있다.
■ \( t = 0 \)에서 \( u_1 = 1, u_2 = 0 \)이라고 한다면, 초기 조건을 \( u(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \)로 나타낼 수 있다.
■ \( \dfrac{du}{dt} = Au \)를 \( u'(t) \)와 \( u(t) \)를 이용해 나타낸다면 행렬 \( A \)는 두 선형미분방정식의 계수로 구성된다는 것을 확인할 수 있다.

■ 초기 조건을 \( u(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \)로 했기 때문에 \( t \)가 time이라고 했을 때, 시간이 지나면 \( \dfrac{du_2}{dt} \)는 양수가 될 것이다. 왜냐면 \( \dfrac{du_2}{dt} \)는 \( u_1 - 2u_2 \)로 정의되었기 때문이다.
■ 행렬 \( A \)의 고윳값과 고유벡터를 통해 시간이 지남에 따라 미분방정식 \( u'_1 \)과 \( u'_2 \)가 어떻게 변하는지를 알 수 있다.
■ 행렬 \( A \)의 고유방정식은 \( \lambda^2 + 3 \lambda = 0 \)이므로 행렬 \( A \)의 고윳값 \( \lambda = 0, -3 \)이다.
■ 각 \( \lambda \)에 대응하는 고유벡터는 \( (A - \lambda I) \mathbf{x} = 0 \)의 해인 영공간을 구하면 된다.
- \( \lambda_1 = 0 \)에 대응하는 고유벡터는 \( \mathbf{x}_1 = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \)
- \( \lambda_2 = -3 \)에 대응하는 고유벡터는 \( \mathbf{x}_2 = \begin{bmatrix} -1 \\ 1 \end{bmatrix} \)
■ 고윳값과 고유벡터로 \( u(t) \)에 대한 일반해를 나타낼 수 있다. 이 예에서 행렬 \( A \)는 두 개의 고윳값과 고유벡터를 가진다. 이때 이 예의 \( u(t) \)에 대한 일반해는 두 개의 special solution인 지수 해의 조합 \( u(t) = c_1 e^{\lambda_1 t} \mathbf{x}_1 + c_2 e^{\lambda_2t} \mathbf{x}_2 \)으로 표현할 수 있다.
■ 이 해들은 미분방정식의 해가 된다. 방정식 \( \dfrac{du}{dt} = Au \)에 순수 해 \( u = e^{\lambda_1 t} \mathbf{x}_1 \)을 넣으면,
- 좌변은 지수 함수의 미분이므로 \( \lambda_1 e^{\lambda_1 t} \mathbf{x}_1 \), 우변은 \( A e^{\lambda_1 t} \mathbf{x}_1 \)이므로
- \( \lambda_1 e^{\lambda_1 t} \mathbf{x}_1 = A e^{\lambda_1 t} \mathbf{x}_1 \)가 되고 양변의 지수함수를 나누면
- \( \lambda_1 \mathbf{x}_1 = A \mathbf{x}_1 \)로 고유값과 고유벡터의 정의가 되면서 성립하는 것을 볼 수 있다.
- 즉, 미분방정식의 해로 지수함수 형태 \( u = e^{\lambda_1 t} \mathbf{x}_1 \)를 넣었을 때, 식이 성립하므로 지수함수 형태가 미분방정식의 해가 됨을 알 수 있다.
■ \( c_1, c_2 \)는 \( u(t) = c_1 e^{0 \cdot t} \begin{bmatrix} 2 \\ 1 \end{bmatrix} + c_2 e^{-3 \cdot t} \begin{bmatrix} -1 \\ 1 \end{bmatrix} \)에 초기 조건 \( u(0) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \)을 이용해서 계산할 수 있다.
- 계산하면, \( 2c_1 - c_2 = 1, c_1 + c_2 = 0 \rightarrow c_1 = \dfrac{1}{3}, c_2 = - \dfrac{1}{3} \)
■ 고윳값과 고유벡터 그리고 \( c_1, c_2 \)를 모두 구했으므로 미분방정식의 일반해 \( u(t) = \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} - \dfrac{1}{3} e^{-3t} \begin{bmatrix} -1 \\ 1 \end{bmatrix} \)으로 나타낼 수 있다.
■ \( t \)가 시간이므로, 변하는 값이다. \( u(\infty) = \dfrac{1}{3} \begin{bmatrix} 2 \\ 1 \end{bmatrix} \)이므로 \( t \to \infty \)로 갈 때, \( u_1 = 0.666..., u_2 = 0.333... \)으로 수렴한다는 것을 알 수 있다.
■ 이 예에서 이러한 결과가 나온 이유는 일반해 \( u(t) \)의 첫 번째 항에서 \( \lambda_1 = 0 \)이므로 첫 번째 항의 지수함수 값이 1이 되었고, 두 번째 고윳값이 음수여서 \( t \)가 무한대로 갔을 때 \( e^{-\infty} = 0 \)이므로 \( t \to \infty \)로 갈 때 수렴이 가능한 것이다.
- 이렇게 미분방정식이 시간이 지남에 따라 수렴하는 상태를 정상상태(steady state)라고 부른다.
- 그리고 해가 특정 정상상태에 가까워지는 상태일 때, 정상상태가 안정성(=수렴성)을 가진다고 한다. 반대로 해가 정상상태에 멀어지면 불안정하다고 한다.
■ 즉, 미분방정식을 행렬을 통해 계산할 때, 행렬의 고윳값에 따라 미분방정식의 해가 수렴할 수도 있고, 발산할 수도 있고, 0이 될 수도 있다.
- (1) Stability - 미분방정식의 해가 0으로 수렴하는 경우
- 이때는 \( u(t) \)가 0으로 가는 것이다. \( u(t) to 0 \)
- 그리고 초기 조건이 무엇이든 해가 0으로 가는 경우는 고윳값이 음의 고윳값을 가질 때이다. \( \text{all} \lambda < 0 \)
- (2) Steady state - 미분방정식의 해가 특정 값으로 수렴하는 경우
- 이때는 \( u(t) \)가 어떤 특정 값으로 가는 것이다. \( u(t) to c \)
- 항상 같은 방향의 정상 상태를 가질 수 있는 경우(\( u(t) to c \))는 위의 예시처럼 하나의 고윳값이 0이고 나머지 고윳값은 음수인 경우이다. \( \lambda_1 = 0 \text{ and other } \lambda < 0 \)
- (3) Divergence- 미분방정식의 해가 발산하는 경우
- 발산하는 경우는 고윳값이 단 한 개라도 0보다 큰 값을 갖는 경우이다. \( \text{any } \lambda > 0 \)
- 그래야 지수함수를 통해 항상 발산하는 상태가 된다.
4. 행렬 지수함수(Matrix exponential)
■ 방정식 \( \dfrac{du}{dt} = Au \)에서 행렬 \( A \)는 벡터 \( u \)와 \( u \)의 미분값인 \( u' \)을 연결시키는 역할을 한다.
■ 미분방정식의 일반해 \( u = c_1 e^{\lambda_1 t} \mathbf{x}_1 + c_2 e^{\lambda_2t} \mathbf{x}_2 \)를 고유벡터 \( \mathbf{x}_1, \mathbf{x}_2 \)를 열벡터로 가지는 고유벡터행렬로 다음과 같이 분해할 수 있다.
\( \begin{bmatrix} u_1 \\ u_2 \end{bmatrix} =
\begin{bmatrix} | & | \\ \mathbf{x}_1 & \mathbf{x}_2 \\ | & | \end{bmatrix}
\begin{bmatrix} c_1 e^{\lambda_1 t} \\ c_2 e^{\lambda_2 t} \end{bmatrix} \)
■ 여기서 고유벡터행렬을 \( S \), 지수함수들을 \( v \)라고 하면 \( u = c_1 e^{\lambda_1 t} \mathbf{x}_1 + c_2 e^{\lambda_2t} \mathbf{x}_2 \)는 \( u = Sv \)로 분해시킬 수 있다.
■ \( u = Sv \)를 \( \dfrac{du}{dt} = Au \)에 대입하면
■ \( \dfrac{du}{dt} \)는 \( u \)를 \( t \)로 미분한다는 의미이므로 \( u = Sv \)를 대입했을 때, \( t \)가 없는 행렬 \( S \)는 상수 취급하여 밖으로 빼낼 수 있고, \( t \)가 있는 \( v \)는 남겨야 하므로
■ \( u = Sv \)를 \( \dfrac{du}{dt} = Au \)에 대입하면 \( \dfrac{du}{dt} = Au \rightarrow S \dfrac{dv}{dt} = A S v \)로 나타낼 수 있다.
■ 그다음, \( S \frac{dv}{dt} = A S v \)의 양변의 좌측에 \( S \)의 역행렬을 곱하면 \( \dfrac{dv}{dt} = S^{-1} A S v \)가 된다.
■ 이때, \( S \)는 행렬 \( A \)의 고유벡터들로 이루어진 고유벡터행렬이므로 \( S^{-1}AS = \Lambda \) 대각행렬로 나타낼 수 있다.
■ 그러므로, \( u = Sv \)를 \( \dfrac{du}{dt} = Au \)에 대입하면 \( \dfrac{dv}{dt} = S^{-1} A S v = \Lambda v \)가 된다.
■ 대각행렬 \( Lambda \)의 계산 값은 상수이므로, \( \dfrac{dv}{dt} = \Lambda v \)는 벡터 \( v \)를 \( t \)로 미분한 것은 벡터 \( v \)에 어떤 상수를 곱한 것과 같다는 의미가 된다.
- \( \dfrac{dv}{dt} = \Lambda v \Leftrightarrow \begin{bmatrix} v_1' \\ v_2' \end{bmatrix} = \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \)이므로
- \( \dfrac{dv_1}{dt} = \lambda_1 v_1 \Leftrightarrow \dfrac{d(c_1 e^{\lambda_1 t})}{dt} = \lambda_1 c_1 e^{\lambda_1 t} \)
- \( \dfrac{dv_2}{dt} = \lambda_2 v_2 \Leftrightarrow \dfrac{d(c_2 e^{\lambda_2 t})}{dt} = \lambda_2 c_2 e^{\lambda_2 t} \)가 되어 \( \dfrac{dv}{dt} = \Lambda v \)이 성립하는 것을 확인할 수 있다.
■ \( \dfrac{dv}{dt} = \Lambda v \) 식을 이용하여 미분방정식을 자연스럽게 표기할 수 있다.
■ \( \dfrac{dv}{dt} = \Lambda v \rightarrow \int \dfrac{1}{v} dv = \int \Lambda \, dt \rightarrow \ln |v| + C_1 = \Lambda t + C_2 \rightarrow |v| = e^{\Lambda t + C_2 - C_1} = e^{\Lambda t} \cdot e^{C_2 - C_1} \rightarrow v = C e^{\Lambda t} \)
■ \( v = C e^{\Lambda t} \)식을 미분방정식의 해를 구하기 위해 함수의 형태 \( v(t) \)로 바꿔야 한다. 이렇게 함수의 형태로 바꿀 때, 반드시 초깃값이 있어야 한다. \( t = 0 \)일 때 \( v(0) = \begin{bmatrix} c_1 \\ c_2 \end{bmatrix} \)가 된다.
■ 이 상수 벡터 \( v(0) \)을 \( v = C e^{\Lambda t} \)식의 상수 \( C \)로 대체할 수 있다. 이렇게 해서 \( v(t) = e^{\Lambda t} v(0) \)으로 정의할 수 있다.
■ \( u = Sv \)를 \( t \)에 대한 함수 형태로 나타내면 \( u(t) = Sv(t) \)이다. \( u(t) = Sv(t) \)에 \( v(t) = e^{\Lambda t} v(0) \)를 대입하면 \( u(t) = S e^{\Lambda t} v(0) \)이 된다.
■ 이때의 초깃값 \( u(0) = Se^0v(0) = Sv(0) \)이며, \( u(0) = Sv(0) \rightarrow v(0) = S^{-1}u(0) \)이 된다.
■ \( u(t) = S e^{\Lambda t} v(0) \)는 \( u(t) = S e^{\Lambda t}S^{-1} u(0) \)가 되고
■ 지수함수를 밑으로 하는 형태의 행렬인 행렬지수함수 \( e^{At} = Se^{\Lambda t}S^{-1} \)을 통해 \( u(t) = S e^{\Lambda t}S^{-1} u(0) \)를 \( u(t) = e^{A t} u(0) \) 으로 정의할 수 있다.
cf) 테일러 급수(테일러 전개)
- \( n \)번 미분이 가능한 어떤 함수 \( f(x) \)에 대해, \( f(x) \)와 \( f(x) \)의 도함수들의 '한 점'에서의 값으로 계산된 항들의 무한합으로 나타내는 방법이다.
- 1계 도함수는 1!, 2계 도함수는 2!, ... 으로 n계 도함수에 대해 각각 n!으로 나눈다.
\( f(x) = f(a) + \dfrac{f'(a)}{1!} (x-a) + \dfrac{f''(a)}{2!} (x-a)^2 + \dfrac{f'''(a)}{3!} (x-a)^3 + \dots + \dfrac{f^{(n)}(a)}{n!} (x-a)^n = \displaystyle\sum_{n=0}^{\infty} \dfrac{f^{(n)}(a)}{n!} (x-a)^n \)
- 테일러 급수에 한 점이 \( x = 0 \)일 때의 테일러 급수를 매클로린 급수라고 한다. \( f(x) = \displaystyle\sum_{n=0}^{\infty} \dfrac{f^{(n)}(0)}{n!} x^n \)
- 이렇게 유한번의 연산으로 구할 수 있는 \( f(x) \)를 테일러 급수로 나타낼 수 있다. 이 점을 이용하면, 다항함수가 포함된 다항식의 근으로 나타낼 수 없는 초월 함수인 지수 함수나 sin, cos 함수에 대해서도 근사할 수 있다.
- \( e^x = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots + \dfrac{x^n}{n!} = \sum_{n=0}^{\infty} \dfrac{x^n}{n!} \)는 \( x = 0 \)일 때의 매클로린 급수를 통해 지수 함수 \( e^x \)를 전개한 것이다.
- \( \dfrac{1}{1 - x} = 1 + x + x^2 + x^3 + \dots + x^n = \sum_{n=0}^{\infty} x^n \), \( \; |x| < 1 \)는 \( x = 0 \)일 때의 매클로린 급수를 통해 기하 급수를 전개한 것이다.
■ \( e^x = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dots + \dfrac{x^n}{n!} = \displaystyle\sum_{n=0}^{\infty} \dfrac{x^n}{n!} \)를 통해 행렬지수함수 \( e^{At} \)를 다음과 같이 나타낼 수 있다.
\( e^{At} = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \dots + \dfrac{(At)^n}{n!} = \displaystyle\sum_{n=0}^{\infty} \dfrac{(At)^n}{n!} \)
■ 그리고 \( \dfrac{1}{1 - x} = 1 + x + x^2 + x^3 + \dots + x^n = \sum_{n=0}^{\infty} x^n \), \( \; |x| < 1 \)는 \( x = 0 \)를 통해 \( (I - At)^{-1} = I + At + (At)^2 + (At)^3 + \dots + (At)^n = \sum_{n=0}^{\infty} (At)^n \), 여기서 행렬 \( At \)의 고윳값 \( \lambda \)의 절댓값은 1보다 작아야 한다. \( | \lambda\; of\; At | < 1 \)
■ \( u(t) = Se^{ \Lambda t} S^{-1} u(0) = e^{At} u(0) \)에서 \( e^{At} = Se^{ \Lambda t} S^{-1} \)가 되는 이유는 행렬지수함수 \( e^{At} = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \dots + \dfrac{(At)^n}{n!} = \displaystyle\sum_{n=0}^{\infty} \dfrac{(At)^n}{n!} \)를 이용해 확인할 수 있다.
- 대각화 가능하면 \( A = S \Lambda S^{-1} \)를 이용하면, 행렬의 멱승에 대해 \( A^n = S \Lambda^n S^{-1} \)으로 계산할 수 있다. \( A = S \Lambda S^{-1} \)로 치환하여 \( e^{At} = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \dots + \dfrac{(At)^n}{n!} \)를 전개하면
- \( e^{At} = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \dots + \dfrac{(At)^n}{n!} = I + S \Lambda S^{-1} t + \dfrac{S \Lambda^2 S^{-1} t^2}{2!} + \dfrac{S \Lambda^3 S^{-1} t^3}{3!} + \dots + \dfrac{S \Lambda^n S^{-1} t^n}{n!} \)
- 이때 단위행렬 \( I \)는 \( I = S S^{-1} \)로 나타낼 수 있다. 그러므로 전개한 식을 다음과 같이 \( S \)와 \( S^{-1} \)로 묶으면
- \( e^{At} = S \left( I + \Lambda t + \dfrac{\Lambda^2 t^2}{2!} + \dfrac{\Lambda^3 t^3}{3!} + \cdots + \dfrac{\Lambda^n t^n}{n!} \right) S^{-1} \)이 되며 \( I + \Lambda t + \dfrac{\Lambda^2 t^2}{2!} + \dfrac{\Lambda^3 t^3}{3!} + \cdots + \dfrac{\Lambda^n t^n}{n!} \)는 \( e^{ \Lambda t} \)를 전개한 것이다.
- 그러므로 \( e^{At} = S e^{ \Lambda t} S^{-1} \)로 나타낼 수 있다. 단, 이렇게 나타내기 위해서는 \( A \)가 대각화 가능해야 한다. 즉, \( A \)는 서로 독립인 \( n \)개의 고유벡터를 가져야 한다.
- 즉, 행렬 \( A \)가 대각화 가능한 행렬이면 행렬지수함수는 \( e^{At} = S e^{ \Lambda t} S^{-1} \)로 계산할 수 있고, 행렬 \( A \)가 대각화 가능하지 않다면 \( e^{At} = I + At + \dfrac{(At)^2}{2!} + \dfrac{(At)^3}{3!} + \dots + \dfrac{(At)^n}{n!} \)으로 계산해야 한다.
■ \( e^{At} = S e^{ \Lambda t} S^{-1} \)에서 \( e^{\Lambda t} \)는 다음과 같이 구할 수 있다.
■ 대각행렬 \( \Lambda \)는 주대각원소가 상수인 \( \lambda \)이고 나머지 원소는 0인 행렬이다. \( \Lambda =
\begin{bmatrix}
\lambda_1 & & \\
& \lambda_2 & \\
& & \ddots & \\
& & & \lambda_n
\end{bmatrix} \)
■ \( e^{ \Lambda t} \)는 \( \Lambda \)에 숫자 t를 곱한 \( \Lambda t \)를 지수부로 갖는 지수 함수이므로 다음과 같이 나타낼 수 있다.
\( \Lambda t =
\begin{bmatrix}
\lambda_1 t & & \\
& \lambda_2 t & \\
& & \ddots & \\
& & & \lambda_n t
\end{bmatrix} \), \( \quad e^{\Lambda t} = \begin{bmatrix} e^{\lambda_1 t} & & \\ & e^{\lambda_2 t} & \\ & & \ddots & \\ & & & e^{\lambda_n t} \end{bmatrix} \)
■ 미분방정식의 일반해 \( u(t) = S e^{ \Lambda t} S^{-1}u(0) = e^{At} u(0) \)에서 \( S e^{ \Lambda t} S^{-1}u(0) \)를 보면, \( u(0) \)는 초깃값이므로 고정된 값이고, 고유벡터행렬 \( S \)도 결국 상수이기 때문에 고정되어 있다.
■ 즉, 미분방정식의 일반해에서 \( t \)가 변함에 따라 변하는 부분은 \( e^{ \Lambda t} \)이며, \( e^{ \Lambda t} \)는 \( e^{\Lambda t} = \begin{bmatrix} e^{\lambda_1 t} & & \\ & e^{\lambda_2 t} & \\ & & \ddots & \\ & & & e^{\lambda_n t} \end{bmatrix} \)이므로 \( t \)가 양의 방향으로 나아간다고 가정했을 때, 해가 수렴하기 위해서는 행렬 \( A \)의 모든 고윳값들이 0보다 작아야 한다. 모든 고윳값 \( \lambda \)가 음수여야 \( t \to \infty \)로 갈때 \( e^{-\infty} = 0 \)으로 해가 수렴성(=안정성(stability))을 갖는다.
'선형대수' 카테고리의 다른 글
| Markov matrices (0) | 2025.02.27 |
|---|---|
| [개념] 회전변환, 직교 대각화를 이용한 회전변환 (0) | 2025.02.27 |
| [개념] 대칭행렬의 직교 대각화, 스펙트럼 분해, 2차형식 (0) | 2025.02.24 |
| Diagonalization and powers of A (0) | 2025.02.24 |
| [개념] 행렬의 대각화(Diagonalization) (0) | 2025.02.20 |


