0. 경우의 수, 순열, 조합, 이항정리, 다항 계수
경우의 수
- 곱의 법칙
■ 어떤 사건이 동시에 일어날 때 각 경우의 수를 곱한다.
■ 예를 들어, 주사위 1개를 던졌을 때, 나올 수 있는 경우의 수는 6이고 동전 1개를 던졌을 때 나올 수 있는 경우의 수는 2이다.
동시에 주사위와 동전을 던진다면, 나올 수 있는 경우의 수는 6×2=12
- 합의 법칙
■ ① 동시에 일어날 수 없고 ② 빠짐없이 분류한 다음, 각각의 경우의 수를 더한다.
■ 예를 들어 서울에서 부산까지 갈 수 있는 경우의 수가 다음 그림과 같을 때,

이를 분류하면
- (1) '서 → 대 → 부'의 경우의 수는 곱의 법칙에 의해 2×2
- (2) '서 → 전 → 부'의 경우의 수는 곱의 법칙에 의해 3×2
- (3) '서 → 대 → 전 → 부'의 경우의 수는 곱의 법칙에 의해 3×2×2
- (4) '서 →전 → 대 → 부'의 경우의 수는 곱의 법칙에 의해 3×2×2
- 그러므로 서울에서 부산까지 갈 수 있는 경우의 수는 2×2+3×2+3×2×2+3×2×2
순열(permutation)
- 팩토리얼
■ n개의 객체가 있을 때, 서로 다른(순서를 고려한) n개를 배열할 때, 가능한 경우의 수는 n!
n⋅(n−1)⋅(n−2)⋯3⋅2⋅1=n!
■ 예를 들어 a,b,c라는 문자 3개를 나열할 수 있는 모든 경우의 수는 3!
- 순열
■ n개의 객체가 있을 때, 서로 다른(순서를 고려한) n개 중에 r개를 선택하는 경우의 수는 nPr=n!(n−r)!,(n≥r)
■ 예를 들어, 7명 중 3명을 뽑아서 줄을 세우는 방법의 수는?
■ 순서를 고려하므로 예를 들어 '철수 - 영희 - 민석'과 '철수 - 민석 - 영희'는 다른 경우로 취급한다.
■ 3명을 뽑아 줄을 세우므로, 첫 번째 자리에 올 수 있는 경우의 수는 7, 두 번째 자리에 올 수 있는 경우의 수는 앞에서 1명이 빠졌으니 6, 세 번째 자리에 올 수 있는 경우의 수는 앞에서 2명이 빠졌으므로 5이다.
■ 그러므로 7×6×5=210가지이다. 7!(7−3)!=7!4!=7×6×5
■ n개의 객체가 있을 때, n이 그룹 n1,n2,⋯,nk로 구성되어 있으며, n=n1+n2+⋯+nk라면(= n개 중에서 같은 것이 각각 n1개, n2개, ⋯,, nk개 있을 때), n개를 일렬로 나열하는 순열의 수는 n!n1!⋅n2!⋯nk!이다.
■ 예를 들어 총 10명이 있는데, 그 중에서 신입생은 1명, 2학년은 2명, 3학년은 4명, 4학년은 3명이라면, 학년 순서를 구별하지 않고 줄을 세우는 방법의 수는 10!1!⋅2!⋅4!⋅3!
-10명의 사람을 나열하는 방법은 10!이다.
- 1학년은 1명이므로 1!, 2학년은 2명이므로 2!, 3학년은 4명이므로 4!, 4학년은 3명이므로 3!이다.
조합(combination)
■ 조합은 순열과 달리 순서를 고려하지 않으며, 서로 다른 n개 중에 r개를 선택하는 경우의 수를 의미한다.
nCr=(nr)=n!(n−r)!r!
cf) nCr=nCn−r⇔(nr)=(nn−r)
(nn−r)=n!(n−(n−r))!(n−r)!=n!r!(n−r)!=(nr)
■ 예를 들어, 순열에서는 '철수 - 영희 - 민석'과 '철수 - 민석 - 영희'는 다른 경우로 취급하지만, 조합에서는 같은 경우로 취급한다.
■ 예를 들어 3개의 재료 중 순서를 고려하지 않고, 2개의 재료를 뽑는 경우의 수는 (32)=3!(3−2)!2!
이항정리(Binomial Theorem)
■ 자연수 n에 대하여 다항식 x+y)n을 전개하면
(x+y)n=nC0xn+nC1xn−1y+nC2xn−2y2+⋯+nCrxn−ryr+⋯+nCnyn=n∑i=0(ni)xn−iyi이다. 이렇게 다항식 (x+y)n을 전개하는 것을 이항정리라고 한다.
■ 그리고 n∑i=0(ni)xn−iyi에서 (ni),i=0,1,2,⋯,n을 이항 계수(binomial coefficient)라고 한다. 이항 계수는 이항식을 이항정리로 전개했을 때, 각 항의 계수이며 주어진 것에 대한 순서를 고려하지 않은 조합의 가짓수이다.
■ 예를 들어 (x+y)3을 전개하면, (x+y)3=(30)x0y3+(31)x1y2+(32)x2y1+(33)x3y0=x3+3xy2+3x2y+y3이다.
■ 이때, 예를 들어 x2y항은 세 개의 인수 (x+y) 중 어느 한 인수에서 y를 택하고, 나머지 두 인수에서 각각 x를 택하여 곱한 단항식 yxx,xyx,xxy의 합이다.
■ 즉, x2y의 계수는 세 개의 인수 (x+y) 중 한 개에서 y를 택하는 조합의 수와 같으므로 (31)=3이다.
■ 이 예에서 각 항의 이항 계수는 1 3 3 1이다.
■ 위의 (x+y)n의 전개식에서 xn−ryr항은 n개의 인수 (x+y) 중에서 r개의 인수에서 y를 택하고, 나머지 (n−r)개의 인수에서 x를 택하여 곱한 것이다.
■ 그러므로 xn−ryr의 계수는 n개의 인수 (x+y) 중 r개의 인수에서 y를 택하는 조합의 수와 같다. 즉, nCr와 같다.
■ 이항 계수의 값을 삼각형 모양으로 나열한 것을 파스칼의 삼각형이라고 한다.

■ 위의 (x+y)3의 예에서 각 항의 이항 계수는 1 3 3 1이다.
■ 파스칼의 삼각형을 보면, (x+y)4의 경우 각 항의 이항 계수는 1 4 6 4 1이 된다는 것을 알 수 있다.
다항 계수(multinomial coefficient)
■ 다항 계수는 이항 계수의 개념을 확장한 것으로,
■ 다항 계수는 총 n개의 구별 가능한 item이 있고, 이 n개의 구별 가능한 item을 r개의 구별 가능한 그룹 n1,n2,⋯,nr으로 나눈다면, 나눌 수 있는 방법의 가짓수이다.
■ n=n1+n2+⋯+nr일 때, 다항 계수 (nn1,n2,⋯,nr)은 다음과 같다.
(nn1,n2,…,nr)=n!n1!n2!…nr!
--이와 같은 공식은 (nn1)(n−n1n2)(n−n1−n2n3)⋯(n−n1−⋯−nr−1nr)⇔n!n1!(n−n1)!⋅(n−n1)!n2!(n−n1−n2)!⋯(n−n1−⋯−nr−1)!(n−r)!nr!⇔n!n1!n2!⋯nr!=(nn1,n2,…,nr)
■ 예를 들어, 10명에게 과자 2개, 빵 3개, 음료수 3개, 사탕 2개를 나눠줄 때
- 10명 중 2명에게 과자 2개를 주면, 남은 8명에게는 빵 3개, 음료수 3개, 사탕 2개를 나눠줘야 한다.
- 8명 중 3명에게 빵 3개를 주면, 남은 5명에게는 음료수 3개, 사탕 2개를 나눠줘야 한다.
- 5명 중 3명에게 음료수 3개를 주면, 남은 2명에게는 사탕 2개를 나눠줘야 한다.
- 2명 중 2명에게 사탕 2개를 나눠주면 끝이 난다.
- 이 과정을 다항 계수를 이용하여 계산하면, (102,3,3,2)=10!2!3!3!2!
1. 표본공간과 사상
■ '동일한 조건'에서 '독립적'으로 반복할 수 있는 실험이나 관측을 확률 실험(random experiment) 또는 시행(trial)이라 하며, 확률 실험(<=> 시행)에서 나올 수 있는 결과는 바뀔 수 있지만, 각 결과가 나올 가능성, 확률은 같아야 한다.
- 예를 들어 주사위 던지기, 동전 던지기 등이 있다. 주사위를 던졌을 때, 동전을 던졌을 때 눈금 1 ~ 6, 앞면 혹은 뒷면이 나오는 결과는 바뀔 수 있지만, 주사위 눈금 1이 나올 확률, 6이 나올 확률, ..., 앞면이 나올 확률, 뒷면이 나올 확률은 항상 동일하다.
■ 이렇게 확률 실험을 하여 나타낼 수 있는 가능한 모든 관측 결과의 집합을 표본공간(sample sapce)이라 하며 기호 S로 표기한다.
■ 그리고 표본공간의 요소, 즉 확률 실험을 통해 얻을 수 있는 각각의 결과들을 근원사상(elementary event) 또는 원소(element)라고 하며, 표본공간은 모든 근원사상의 집합이다.
■ 여기서 event는 사건 혹은 사상이라 하며 '내가 관심 있는 확률 실험의 결과이다.' 그리고 event는 표본공간의 부분집합이라 할 수 있다.
- 예를 들어 event 1이 1이 나오는 사건, event 2가 2가 나오는 사건이라 했을 때, 더 단순한 event로 나눌 수 없다면, 그 event를 근원사상(elementary event)이라 한다.
■ 예를 들어 주사위 던지기 실험에서의 표본공간은 S = {1, 2, 3, 4, 5, 6}이다.
이때 event는 특정한, 즉 내가 관심 있는 결과들의 집합이므로 event 1을 홀수, event 2를 짝수라 했을 때 event 1 = {1, 3, 5}, event 2 = {2, 4, 6}이라 할 수 있다. S와 event 1, event 2를 보면 event가 표본공간의 부분집합임을 알 수 있다.
■ 표본공간 S의 사상 A에 대한 여사상(=여사건, complementary event) $ A^c$는 S를 구성하는 원소 중에서 사상 A에 포함되는 원소를 제외한 나머지 원소들의 집합이다.
■ 주사위 던지기의 표본 공간 S = {1, 2, 3, 4, 5, 6} 에서 사상 A가 홀수가 나오는 사건이면 A에 포함된 원소 {1, 3, 5}를 제외한 {2 ,4, 6}이 사건 A에 대한 여사상이다.
■ 표본공간 S의 부분집합으로 사상 A, B가 있을 때 A, B가 동시에 발생하는 사상을 A와 B의 교사상, 사상 A 또는 B가 발생하는 사상을 A와 B의 합사상이라 한다.
■ 표본공간, event(사상, 사건) 등은 집합으로 정의되기 때문에 합집합(A u B), 교집합(A n B), 여집합 Ac연산을 할 수 있다.
■ 만약 사상 A와 B의 공통 원소가 없다면 A와 B는 상호 배반(mutually exclusive)이라 한다. 즉 A n B = ∅인 경우이며, A와 B의 교사상이 공사상(공집합)인 상태이다.
cf) 분배 법칙
$ A n (B u C) = (A n B) u (A n C), A u (B n C) = (A u B) n (A u C)$
cf) 드모르간 법칙
$ (A u B)^c = A^c n B^c, (A n B)^c = A^c u B^c$
2. 확률 정의
■ 확률은 어떤 행위를 n 번 시행했을 때의 발생 빈도( f/n )이다.
이때 무수히 많은 n 번의 시행을 하면 f/n 값이 참값으로 수렴한다고 할 수 있는데, 이를 대수의 법칙(Law of large numbers)이라고 한다.
■ 표본공간 S에 사상 A가 존재할 때, 표본공간 S는 확률 실험의 모든 결과이므로 P(S) = 1이며, 발생할 수 없는 사상의 확률은 0이다. 따라서 사상 A는 표본공간 S의 부분집합이므로, 사상 A가 발생할 확률을 P(A)라 했을 때, 0 ≤ P(A) ≤ 1이 성립한다.
3. 확률의 공리(Axioms of Probability)
■ 공리(axiom)는 가장 기초적인 근거가 되는 명제이다. 자명한 진리로 간주되어 증명할 필요가 없다.
- 예를 들어 a+c=b+c이면 a=b같은 것
■ 확률의 공리 3가지는 다음과 같다.
- 공리 ① 0≤P(A)≤1
- 어떤 사건에 대한 확률은 0과 1사이이다.
- 즉, 확률 값은 음수가 될 수 없고 1을 초과할 수도 없다.
- 공리 ② P(S)=1
- 표본공간의 확률은 1이다.(표본공간에 있는 모든 원소들의 확률을 더하면 1이다.)
- 공리 ③ 만약, 사건 A1,A2,⋯들이 모든 i≠j에 대해서 Ai∩Aj=∅일 때(상호 배반일 때), P(∞⋃i=1Ai)=∞∑i=1P(Ai)
- 표본공간에 있는 각각의 사건들이 모두 상호 배반일 때, 모든 사건들의 합집합에 대한 확률은 각 이벤트들의 확률의 합과 같다.
-- ex) A∩B=∅일 때, P(AUB)=P(A)+P(B)
- 모든 사건이 상호 배반일 때, 적어도 1개의 사건이 발생할 확률은 모든 사건들의 확률의 합으로 구할 수 있다.
4. 확률의 연산
■ 어떤 사상의 확률을 다른 사상들의 확률로부터 구할 때, 기본 원칙은 겹치지 않는 영역의 확률을 구하는 것이다.
■ 예를 들어 합사상 A u B의 확률, P(A u B)는 P(A u B) = P(A) + P(B) - P(A n B)로 정의되는데, 이는 A의 확률과 B의 확률에서 겹치는 영역의 확률인 P(A n B)를 P(A) + P(B)에서 빼주기 때문이다.
따라서 P(A u B u C)도 A와 B, A와 C, B와 C가 겹치는 영역의 확률을 제해야 한다.
단 A와 B와 C가 겹치는 영역의 확률 P(A n B n C)를 더해줘야 한다. 그 이유는 예를 들어

에서 P(A) + P(B) + P(C) - P(A n B) - P(A n C) - P(B n C)를 하면 A의 원소이며, B의 원소이자 C의 원소이기도 한 12, 13이 제외되기 때문이다.
### P(A u B u C)에서 P(A n B n C)를 더하는 이유를 보여주기 위함
A = [1, 2, 3, 10, 11, 12, 13]
B = [4, 5, 6, 12, 13, 14, 15]
C = [7, 8, 9, 10, 11, 12, 13, 14, 15]
combined_A_B_C = A + B + C # P(A) + P(B) + P(C)의 원소에 해당
# P(A n B), P(A n C), P(B n C)의 원소에 해당
intersection_AB = [x for x in A if x in B]
intersection_AC = [x for x in A if x in C]
intersection_BC = [x for x in B if x in C]
print(combined_A_B_C)
print(intersection_AB, intersection_AC, intersection_BC)
```#결과#```
[1, 2, 3, 10, 11, 12, 13, 4, 5, 6, 12, 13, 14, 15, 7, 8, 9, 10, 11, 12, 13, 14, 15]
[12, 13] [10, 11, 12, 13] [12, 13, 14, 15]
````````````
intersection = intersection_AB + intersection_AC + intersection_BC
# P(A) + P(B) + P(C) - P(A n B) - P(A n C) - P(B n C)의 원소에 해당
for i in intersection:
combined_A_B_C.remove(i)
print(i)
print(combined_A_B_C)
```#결과#```
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 15]
````````````따라서 P(A u B u C) = P(A) + P(B) + P(C) - P(A n B) - P(A n C) - P(B n C) + P(A n B n C)가 된다.
■ 사상 A와 B가 상호 배반이면 P(A n B) = 0이므로 P(A u B) = P(A) + P(B)가 된다. 이를 일반화하면,
사건(사상) A1,A2,A3,...가 서로 상호 배반일 때, P(A1∪A2∪A3∪⋯)=P(A1)+P(A2)+P(A3)+⋯ ( 단, Ai∩Aj=∅,모든i≠j))으로 나타낼 수 있다.
■ 그리고 사상 A와 여사상 Ac는 상호 배반이다. 따라서 P(A∪Ac)=P(A)+P(Ac)=1이 성립하므로 P(Ac)=1−P(A)가 된다.
- 이와 유사하게 사상 B∩A,B∩Ac)는 상호 배반이고, B=(B∩A)∪(B∩Ac)로 표현할 수 있으므로 P(B)=P(B∩A)+P(B∩Ac)이 성립한다.
- 이외에도 P(Ac∩Bc)=1−P(A∪B),P(Ac∪Bc)=1−P(A∩B)가 성립한다.
- 드모르간 법칙에 의해Ac∩Bc=(A∪B)c,Ac∪Bc=(A∩B)c이다.
여사건의 확률 P(Ac)=1−P(A)에 의해 P(Ac∩Bc)=P((A∪B)c)=1−P(A∪B),P(Ac∪Bc)=P((A∩B)c)=1−p(A∩B)가 성립한다.
5. 확률의 기본 성질
■ 정리하면, 확률의 기본 성질은 다음과 같다.
- ① P(Ac)=1−P(A)
- ② 만약, A⊂B이라면, P(A)≤P(B)이다.
- A가 B에 속한다는 것을, 전체 표본공간 S안에 B가 있고, B안에 A가 있다고 생각해보자.( 정확하게는 A와 B∩Ac의 합집합이 B가 된다. B=A∪(B∩Ac))
- 즉, B=A+(B∩Ac)으로 B를 A와 (B∩Ac)로 나눌 수 있다.
- P(B)=P(A)+P(B∩Ac)에서 사건 A와 사건 B∩Ac는 공통 원소가 없으므로 확률을 단순히 더할 수 있다. (공리 ③)
- 확률은 음수가 될 수 없으므로 P(B∩Ac)≥0이다. 그러므로 위의 식에서 P(A)≤P(B)가 된다.
- 예를 들어, 표본공간 S=1,2,3,4,5,6에서 사건 A를 A={2}, 사건 B를 B={2,4,6}이라고 한다면, A={2}⊂B={2,4,6}이며, P(A)=1/6,P(B)=1/2
- ③ P(A∪B)=P(A)+P(B)−P(A∩B)
- ③을 포함배제의 원리라고 부른다. 포함배제의 원리는 두 개 이상의 합집합을 구할 때 중복된 부분은 제외해야 한다는 개념이다.
6. 조건부 확률
■ 어떤 사건(사상)이 발생했다는 전제하에 다른 사건(사상)이 발생할 확률을 조건부 확률(conditional probability)이라고 한다.
■ 사건 B가 발생했다는 조건이 주어졌을 때 사건 A의 조건부 확률은 다음과 같다.
P(A∣B)=P(A∩B)P(B)단, (P(B)>0)
- 이때 조건이 되는 사건 B는 축소된 표본공간 역할을 하게 된다. 우리가 이미 어떤 사건 B가 발생했음을 알고 있기 때문이다.
즉, 원래의 표본공간에서 B라는 사건이 발생한 경우만 고려하므로, 전체 표본공간이 B로 축소된다고 할 수 있다.
따라서 P(A∣B)는 새로운 표본공간인 사건 B에서 사건 A n B, 두 사상 A와 B가 동시에 발생할 확률을 의미한다.
■ 만약, 사건 A와 사건 B가 상호 배반이라면 P(A∩B)=0이므로, 조건부 확률 P(A∣B)=P(A∩B)P(B)=0P(B)=0이 된다.
■ 그리고 사건 A와 사건 B의 관계가 B⊂A라면, A∩B=B가 된다. 즉 P(A∩B)=P(B). 그러므로, 조건부 확률 P(A∣B)=P(A∩B)P(B)=P(B)P(B)=1이 된다.
7. 확률의 곱의 법칙(Multiplicative Rules)
■ 두 사건의 교집합의 확률은 P(A∩B)=P(A∣B)⋅P(B)=P(B∣A)⋅P(A)단, (P(A)>0,P(B)>0)
- 3개의 사건으로 확장하면 P(A∩B∩C)=P((A∩B)∩C)=P(A∩B)⋅P(C∣A∩B)=P(A)⋅P(B∣A)⋅P(C∣A∩B)가 된다. (*조건부 확률 정의를 이용하면 P(A∩B)=P(A)⋅P(B∣A))
- 따라서 n개의 사건이면
P(A1∩A2∩A3∩...∩An)=P(A1)⋅P(A2∣A1)⋅P(A3∣A1∩A2)....P(An∣A1∩A2∩....∩An−1)이 성립한다.
8. 독립 사건(사상)
■ 사건 A, B에 대하여 사건 B가 발생했다는 사실이 사건 A가 발생할 가능성에 영향을 미치지 않으면, 즉 사건 B가 사건 A의 확률에 영향을 주지 않는다면 P(A∣B)=P(A)가 된다.
■ 조건부 확률 정의에 의해 P(A∣B)=P(A∩B)P(B)=P(A)이므로 P(A∩B)=P(A)⋅P(B)가 된다.
또한 P(B∩A)=P(A∩B)P(A)=P(A)⋅P(B)P(A)=P(B)가 된다.
즉, 사건 B가 사건 A의 확률에 영향을 미치지 않으면, 사건 A도 사건 B의 확률에 영향을 미치지 않는 것이다.
이런 상태를 '두 사건 A와 B가 서로 독립(independent)이다.'라고 한다.
따라서 P(A∩B)=P(A)⋅P(B)단, (P(A)>0,P(B)>0)가 성립하면 두 사건 A와 B는 서로 독립인 것으로 이해할 수 있다.
- 만약 사건이 A1,A2,...,An로 사건이 n개 있을 때, A1,A2,...,An이 서로 독립이면,
P(A1∩A2∩⋯∩An)=P(A1)⋅P(A2)⋯P(An)이 성립한다.
- 그리고 반대 개념으로 두 사건 A와 B가 서로 독립이 아닌 경우, 즉, 한 사건이 다른 사건에 영향을 준다면
P(A∩B)≠P(A)⋅P(B) '두 사건 A와 B는 서로 종속(dependent)이다.'라고 한다.
■ 사건이 서로 독립적인 예로는, A와 B가 서로 독립이면 A와 Bc, Ac와 B, Ac와 Bc도 서로 독립이다.
■ 이번에는 사건 3개 A,B,C가 독립인 경우이다. 사건 A,B,C가 독립이면, 사건 A는 B∪C와도 독립이다.
P(A∩(B∪C))=P((A∩B)∪(A∩C))=P(A∩B)+P(A∩C)−P(A∩B∩C)=P(A)P(B)+P(A)P(C)−P(A)P(B∩C)=P(A)[P(B)+P(C)−P(B∩C)]=P(A)P(B∪C)
9. 베이즈 정리(Bayes' theorem)
■ 베이즈 정리는 조건부 확률을 직접 계산하기 어려운 경우, 조건이 되는 사건을 상호 배반 사건들로 분할(partition)하여 조건부 확률을 계산하기 위한 공식이다.
■ 베이즈 정리를 알기 위해선 먼저 '분할(partition)'과 이 개념을 기반으로 하는 전확률 정리에 대해 알아야 한다.
■ 먼저 k개의 집합 B1,B2,...,Bk가 어떤 표본공간 S의 분할이 되려면
1) B1,B2,...,Bk는 각각 서로소여야 한다. B1,B2,...,Bk는 집합이므로, 집합이 서로소가 되야 한다는 것이며, 이는 B를 무작위로 선택했을 때 겹치는 부분이 없어야 한다는 의미이다.
2) B1,B2,...,Bk를 합집합했을 때, 합집합 연산의 결과는 표본공간 S가 되야 한다.
이 두 조건을 만족했을 때 B1,B2,...,Bk를 S의 분할이라고 한다.
- 예를 들어 다음과 같이 B1,B2,B3는 각각 겹치는 부분이 없으며, B1,B2,B3를 합집합하면 S가 된다.
따라서 B1,B2,B3는 S의 분할이라고 할 수 있다.

■ 다음으로 전확률 정리란, 표본공간 S를 상호 배반인 사건 B1,B2,...,Bk, ( Bi∩Bj=∅,i≠j,B1∪B2∪...∪Bk=S )로 분할했을 때, 임의의 사건 A에 대해 P(A)=∑ki=1P(Bi∩A)=∑ki=1P(A∣Bi)P(Bi)=P(A∣B1)P(B1)+P(A∣B2)P(B2)+⋯+P(A∣Bk)P(Bk)가 성립함을 말한다.
- 위의 식이 성립하는 이유는 다음과 같다.
A=A∩S=A∩(B1∪B2∪⋯∪Bk)=(A∩B1)∪(A∩B2)∪⋯∪(A∩Bk)이다. 이 식이 성립하는 이유는 사건 B1,B2,...,Bk가 서로 겹치지 않기 때문에 사건 A의 확률을 사건 A∩B1,A∩B2,⋯,A∩Bk의 확률의 합으로 구할 수 있기 때문이다.
이를 그림으로 표현하자면 다음 그림과 같은 상황인 것이다.
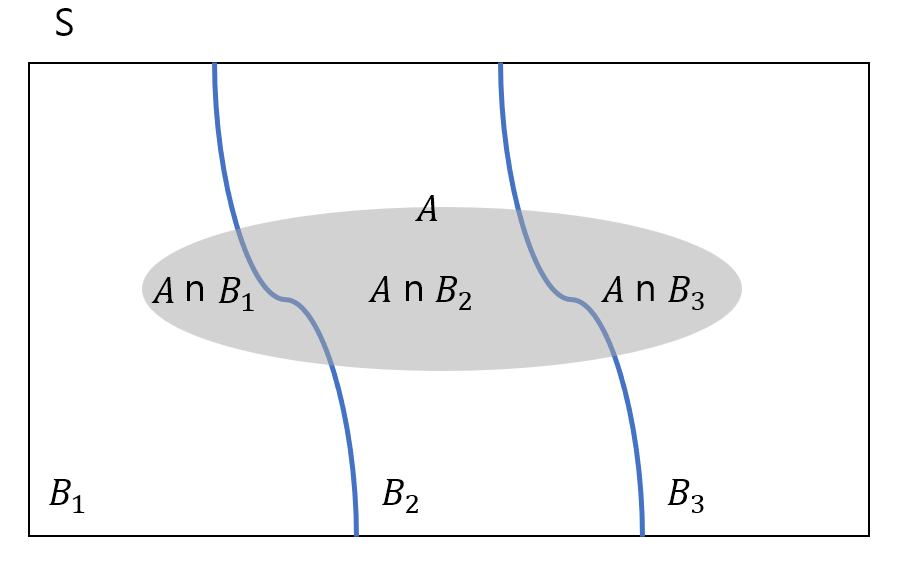
따라서 P(A)=P(A∩B1)+P(A∩B2)+⋯+P(A∩Bk)=∑ki=1P(A∩Bi)가 되며, 곱의 법칙에 의해서 P(A∩Bi)=P(A∣Bi)⋅P(Bi)가 성립한다.
■ 베이즈 정리는 어떤 사건 A가 관측되기 이전의 확률(사전 확률, P(Br))로부터 사건 A가 관측된 후의 조건부 확률(사후 확률, P(Br∣A))을 구하기 위한 것으로 다음의 식이 성립한다.
표본공간 S를 공사상이 아닌(<=>P(Bi)≠0,i=1,2,...,k), 상호 배반인 사건 B1,B2,...,Bk들로 분할하면 공사상이 아닌(<=> P(A)≠0), 임의의 사건 A에 대하여
P(Br∣A)=P(Br∩A)P(A)=P(Br∩A)∑ki=1P(Bi∩A)=P(A∣Br)P(Br)∑ki=1P(A∣Bi)P(Bi)이 성립한다.
■ 베이즈 정리는 예를 들어 불량 제품이 나왔을 때, 이 불량 제품이 생산 라인 A에서 생산되었을 확률을 구하는 문제에 적용할 수 있다.
| 생산 라인 | A | B | C | D |
| 생산 비율 | 20% | 40% | 30% | 10% |
| 불량률 | 4% | 2% | 1% | 5% |
불량률이 나온 사건을 F라 하면, P(F)=P(F∣A)⋅P(A)+P(F∣B)⋅P(B)+P(F∣C)⋅P(C)+P(F∣D)⋅P(D)=0.008+0.008+0.003+0.005=0.024이므로 각 생산 라인에서 불량 제품이 생산되었을 확률은 P(A∣F)=0.2⋅0.040.0.24=0.33...,P(B∣F)=0.4⋅0.020.0.24=0.33...,P(C∣F)=0.3⋅0.010.0.24=0.125,P(D∣F)=0.1⋅0.050.0.24=0.208333...
이때, 사건 F일 때 사건 A일 확률이므로 P(A)=0.2는 사전(prior)확률이며, P(A \mid F) ≒ 0.33 이 사후(posterior) 확률이 되는 것이다.
10. Odds
■ 오즈(또는 아즈)는 사건 A 가 발생하지 않을 경우 대비 발생할 확률. 즉, \dfrac{P(A)}{P(A^c)} = \dfrac{P(A)}{1-P(A)} 를 의미한다.
- 만약, 사건 A 의 성공 확률이 1이라면, \dfrac{P(A)}{1-P(A)} = \dfrac{1}{0} 이므로 Odds는 \infty 의 값을 갖게 된다.
- 사건 A 의 성공 확률이 0이라면, \dfrac{P(A)}{1-P(A)} = \dfrac{0}{1} 이므로 Odds는 0의 값을 갖게 된다.
- 예를 들어 \dfrac{P(A)}{1-P(A)} = \dfrac{1}{4} 라면, P(A) = 1 / 5 임을 알 수 있다.
'확률' 카테고리의 다른 글
| 연속형 확률분포 (1) (0) | 2025.02.14 |
|---|---|
| 적률생성함수 (5) | 2025.02.14 |
| 이산형 확률분포 (0) | 2025.02.14 |
| 확률변수의 기댓값과 분산, 공분산, 상관계수 (0) | 2025.02.05 |
| 확률변수와 확률분포 (0) | 2024.09.03 |



