1. 확률변수(random variable)
■ 확률 변수는 '확률 실험의 각 결과인 표본공간의 각 원소를 실수 값으로 바꾸는 함수'이다.
즉, 표본공간 S에서 실수 공간 R으로의 함수이다.
■ 하나의 확률실험에 대해 여러 개의 확률변수를 정의할 수 있으며, 원소의 개수에 비례하는 확률분포를 갖는다.
■ 확률변수는 보통 알파벳 대문자 (X,Y,Z)로 표기한다.
■ 예를 들어 동전을 두 번 던져 앞면(H)와 뒷면(T)을 관측하는 실험에서의 표본공간 S = {(H, H), (H, T), (T, H), (T, T)}로 4개의 원소를 갖는다.
- 내가 관심 있는 경우가 뒷면이 나오는 횟수라면, 나올 수 있는 경우의 수는 0, 1, 2 중 하나가 된다.
- 즉, 확률변수 X를 뒷면이 나오는 횟수로 정의하면, 확률변수는 표본공간의 각 원소를 숫자로 바꾼다. 이를 그림으로 나타내면 다음과 같다.

- 확률 변수는 원소의 개수에 비례하는 확률 분포를 가지는데, 예를 들어 X=1(동전을 두 번 던졌을 대, 하나만 뒷면이 나오는 경우는 2번)에 해당하는 원소는 HT, TH로 2개 이므로 P(X=1)=24가 된다.
1.1 이산확률변수, 연속확률변수
■ 표본공간 S의 원소가 유한개 또는 셀 수 있는 무한개의 원소로 구성되어 있으면, 이산표본공간(discrete sample space)이라 하고, 표본공간 S가 실선 상의 임의의 구간으로 나타낼 수 있을 때(<=> 원소를 셀 수 없을 때) 연속표본공간(continuous sample space)라고 한다.
■ 예를 들어 주사위, 동전 던지기, 불량품 개수 등은 이산 표본공간, 일별 강수량, 제품의 치수 등은 연속 표본공간에 해당된다.
■ 이산표본공간, 연속표본공간의 정의와 유사하게 확률변수 X가 유한개 또는 셀 수 있는 무한개의 값을 가지면 이산확률변수(discrete random variable), 확률변수 X의 함수 값이 임의의 구간에서 어떠한 값도 가질 수 있을 때 연속확률변수(continuous random variable)라고 한다.
■ 즉 확률변수는 '셀 수 있는가?'를 기준으로 이산확률변수, 연속확률변수로 나뉘며 이산, 연속확률변수도 확률변수이므로 이산확률분포, 연속확률분포를 갖는다.
■ 예를 들어 이산확률변수가 불량품의 개수, 연속확률변수가 일별 주식 가격이라면 이들의 확률분포는 다음 그림과 같이 표현된다.

■ 주의할 점은 연속표본공간으로 얼마든지 이산확률변수를 정의할 수 있다는 점이다.
■ 예를 들어 제품 치수를 기준으로 양품(X = 10), 불량품(X = 1)으로 이산확률변수를 정의할 수 있다.
2. 확률분포
■ 확률분포는 '표본공간 S에서 정의된 확률변수 X의 함수 값들이 발생할 확률을 계산하는 것'을 말하며,
■ 이산확률변수가 생성하는 확률분포를 이산확률분포, 연속확률변수가 생성하는 확률분포를 연속확률분포로 나눈다. 이렇게 나누는 이유는 확률을 계산하는 방법이 다르기 때문이다.
■ 이산확률분포의 함수를 확률질량함수(probability mass function), 연속확률분포의 함수를 확률밀도함수(probability density function)라 하며, 두 함수를 통칭해서 확률분포함수(probability distribution function)라고 한다.
■ 이산확률분포(discrete probability distribution)는 '셀 수 있는(이산적인) 값을 갖는 확률변수의 확률분포'로서, 확률분포함수 f(x)는 P(X=x)를 의미하며 ( f(x)=P(X=x) ), 확률질량함수라고 한다.
■ 이산확률분포는 ∑xf(x)=1 조건과 0≤f(x)≤1for all x 조건을 만족하는데, 각 조건이 의미하는 바는 모든 가능한 결과에 대한 확률의 합은 1이며, f(x)=P(X=x)의 확률은 0 이상 1 이하의 값을 가진다.
■ 확률질량함수는 각 값을 가질 확률을 계산한다.
■ 예를 들어 위의 예시, 동전을 두 번 던져 뒷면이 나오는 횟수의 경우, 경우의 수는 0, 1, 2이며, 각 경우의 수의 확률 중 P(X=1)=24 였다. \( P(X = 1) \)을 포함해 모든 경우의 확률질량함수는 다음 표와 같다.
| x | 0 | 1 | 2 |
| \( P(X = x) = P_x(x) | 1/4 | 2/4 | 1/4 |
- f(x)의 확률이 0이상 1이하이며, 모든 확률의 총합이 1이므로 이산확률분포의 조건을 만족한다.
- 이렇게 확률변수의 특정 값(x)에 대한 확률을 구할 수 있으며, 위의 표처럼 나타낸 표를 확률분포표라고 한다.
■ 연속확률분포(continuous probability distribution)는 셀 수 없는(연속적인) 값을 갖는 확률변수의 확률분포로서, 확률분포함수 f(x)는 확률 P(a<X<b)=∫baf(x)dx를 구하기 위한 확률밀도함수를 의미한다.
■ 즉, 연속확률분포는 연속확률변수 X가 연속적인 값을 갖는 경우로서, 모든 x에 대해 f(x)는 언제나 0 이상의 값을 가지며, f(x) 아래 면적의 합은 1이므로 ∫∞−∞f(x)dx=1, f(x)≥0이라는 조건을 만족한다.
■ 또한, 연속확률분포는 주어진 영역의 면적을 구하여 확률을 계산할 수 있다. P(a<X<b)=∫baf(x)dx

■ 만약 연속확률분포의 확률변수 X가 특정 값(x)과 같은 확률을 구한다면, ( P(X=x)=0 )이 된다.
왜냐하면, P(X=x)=P(x≤X≤x)=∫xxf(y)dy=0이 되기 때문이다.
3. 누적분포함수(cumulative distribution function)
■ 확률분포의 누적분포함수는 '이산형과 연속형 구분 없이 F(x)=P(X≤x)로 정의'된다.
즉, 누적분포함수 F(x)는 확률변수 X의 값이 x이하일 확률을 의미하며, 다음과 같은 특성을 갖는다.
1) 모든 x에 대해 0≤F(x)≤1이며
2) F(x)는 말 그대로 누적이므로x가 커질수록(<=> x=x1,x2,... ), x가 누적되어
X가 x이하일 확률이 증가하거나 최소한 같아지므로 단조 증가 함수라고 할 수 있다.
따라서, x1≤x2이면 항상 F(x1)≤F(x2)가 성립한다.
3) 그리고 F(∞)=P(X≤∞)=1, F(−∞)=P(X≤−∞)=0이 된다.
■ 예를 들어 동전을 두 번 던져 뒷면이 나오는 횟수에서 x = 0, 1 ,2였고, f(0)=14,f(1)=24,f(2)=14이므로 F(x)={0,x<014,0≤x<134,1≤x<21,x≥2가 된다.

■ 이산확률변수인 경우, F(x)=P(X≤x)=∑t≤xf(t),(−∞≤x≤∞)이다.
X가 x1,x2,...,xk,...의 값을 가지고, x1<x2<...<xk<...이면,
F(xn)=n∑k=1f(xk)이고 f(xn)=F(xn)−F(xn−1)이 성립한다.
■ 연속확률변수인 경우, F(x)=P(X≤x)=∫x−∞f(t)dt이며 f(x)=ddxF(x)=F′(x)이다.
■ 예를 들어 다음과 같은 상황은

F(x+2)=F(x)+f(x)·2이며 \( P(x \leq X \leq) = F(x+2) - F(x) = f(x) · 2 \)이다.
- 단위 구간 길이당 확률값은 P(x≤X≤x+2)2이며, 2를 0으로 보내면
f(x)=lim가 된다.
- 미분과 적분의 관계를 고려하면, 누적분포함수를 미분하면 확률밀도함수, 확률밀도함수를 적분하면 누적분포함수가 된다.
4. 결합확률분포(joint probability distribution)
■ 결합확률분포는 2개 이상의 확률변수에 대한 확률분포이다.
■ 2개 이상의 확률변수는 확률변수 간에 서로 영향을 주고 받을 수 있어 동시에 고려할 필요가 있다.
ex) 키와 몸무게, 기온과 강수량
■ 결합확률분포는 두 확률변수 X, Y 가 이산확률변수일 경우, 동시에 각각 x, y 값을 가질 확률이며, (확률변수 X = x 이고 확률변수 Y = y 일 경우의 확률) f(x, y) = P_{X, Y} (x, y) = P(X = x, Y = y) 로 나타낸다.
■ 이산확률변수들의 결합확률분포는 확률변수 X, Y 가 이산적인 값 x, y 를 갖는 경우이고, 모든 x, y 에 대해 확률은 0 이상 1 이하의 값을 가진다. 0 \leq f(x, y) \leq 1 , all x, y 그리고 확률의 총합은 1이므로 \displaystyle \sum_{x} \sum_{y} f(x, y) = 1 을 만족한다.
■ 예를 들어

f(2, 3) = P_{X, Y} (2, 3) = P(X = 2, Y = 3) 은 X = 2 이고 Y = 3 인 경우의 확률이므로 2/20이 된다.
■ 주사위를 두 번 던졌을 때, 최댓값을 X , 최솟값을 Y 라고 한다면, 확률변수 X 와 Y 의 결합확률분포는, 표본공간 S의 원소 개수는 6^2 = 36 개 이며, X = x, Y = y 인 원소의 개수를 n(x, y) = \begin{cases} 1, & \text{if } x = y \\ 2, & \text{if } x > y \end{cases} 라 할 수 있다.
예를 들어 x = 1 일 때 x = y 인 경우는 y = 1 로 한 가지이며, 주사위를 두 번 던지므로 X = 2, Y = 1 인 경우는 주사위가 (1, 2) 또는 (2, 1)이 나오는 2가지이다. X = 3, Y = 1 일 때도 주사위는 (3, 1), (1, 3), X = 3, Y = 2 일 때도 마찬가지로 (3, 2), (2, 3) 2가지이다. X = 4, 5, 6 일 때도 마찬가지이다.
따라서 f(x, y) = \begin{cases} \frac{1}{36}, & \text{if } x = y \\ \frac{2}{36}, & \text{if } x > y \end{cases} , x, y = 1, 2, 3, 4, 5, 6 이라 할 수 있다.
■ 연속형 확률변수 X, Y 가 x, y 라는 연속적인 값을 가질 때의 결합확률분포는, f(x, y) 는 0 이상의 값을 가지므로 f(x, y) \geq 0 이며, 확률의 총합은 1이므로 \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, y) \, dx \, dy = 1 이 된다.
■ 예를 들어 f(x, y) = \dfrac {2(ax + by)}{a + b}, a, b > 0, 0 < X < 1, 0 < Y < 1 일 때
\int_0^1 \int_0^1 \frac{2(ax + by)}{a + b} \, dx \, dy = \frac{2}{a + b} \int_0^1 \int_0^1 (ax + by) \, dx \, dy = \frac{2}{a + b} \int_0^1 \left[ \frac{1}{2} a x^2 + bxy \right]_0^1 \, dy = \frac{2}{a + b} \int_0^1 \left( \frac{1}{2} a + by \right) \, dy = \frac{2}{a + b} \left[ \frac{1}{2} ay + \frac{1}{2} by^{2} \right]_0^1 = \frac{2}{a + b} \cdot \frac{a + b}{2} = 1
이 되므로 f(x, y) 는 a, b > 0 일 때, 0 < x < 1, 0 < y <1 의 범위에서 확률변수 X, Y는 f(x, y) > 0 이며 \int_0^1 \int_0^1 f(x, y) \, dx \, dy = 1 이므로 결합확률분포가 된다는 것을 알 수 있다. 따라서 a, b > 0 이라는 가정 하, 0 < x < 1, 0 < y < 1 의 범위에 속하는 P\left( 0 < X < \frac {1}{2}, \, 0 < Y < \frac {1}{2} \right) 를 구할 수 있다. P\left( 0 < X < \frac {1}{2}, \, 0 < Y < \frac {1}{2} \right) 도 \int_0^{\frac{1}{2}} \int_0^{\frac{1}{2}} f(x, y) \, dx \, dy 이중적분을 계산하여 확률값을 구하면 된다.
5. 주변확률분포(marginal probability distribution)
■ 이산확률변수 X, Y 의 결합확률분포 f(x, y) 로부터 주변확률분포는 다음과 같이 정의할 수 있다. f_X(x) = \displaystyle \sum_{y} f(x, y), \quad f_Y(y) = \displaystyle \sum_{x} f(x, y)
■ 예를 들어 x = 1, 2, 3, 4 , y = 1,2, 3 이면 f_X(x) = f(x, 1) + f(x, 2) + f(x, 3) , f_Y(y) = f(1, y) + f(2, y) + f(3, y) + f(4, y)
■ 연속형일 경우, 주변확률분포는 다음과 같다. f_X(x) = \int_{-\infty}^{\infty} f(x, y) \, dy, \quad f_Y(y) = \int_{-\infty}^{\infty} f(x, y) \, dx
■ 예를 들어 확률변수 X, Y 가 다음과 같을 때,
| Y = 0 | Y = 1 | Y = 2 | |
| X = 0 | 0.1 | 0 | 0.3 |
| X = 1 | 0.2 | 0.15 | 0.25 |
- X 에 대한 주변확률분포는 P(X = 0) = P(X = 0, Y = 0) + P(X = 0, Y = 1) + P(X = 0, Y = 2) = 0.1 + 0 + 0.3 = 0.4 , P(X = 1) = P(X = 1, Y = 0) + P(X = 1, Y = 1) + P(X = 1, Y = 2) = 0.2 + 0.15 + 0.25 = 0.6
- Y 에 대한 주변확률분포는 P(Y=0) = P(X = 0, Y = 0) + P(X = 1, Y = 0) = 0.1 + 0.2 = 0.3 , P(Y=1) = P(X = 0, Y = 1) + P(X = 1, Y = 1) = 0 + 0.15 = 0.15 , P(Y=2) = P(X = 0, Y = 2) + P(X = 1, Y = 2) = 0.3 + 0.25 = 0.55
■ 연속일 경우, \dfrac{2(ax + by)}{a + b}, \quad a, b > 0, \quad 0 < x < 1, \quad 0 < y < 1 에 대해 f_X(x) = \int_0^1 \dfrac{2(ax + by)}{a + b} \, dy = \dfrac{2}{a + b} \int_0^1 (ax + by) \, dy = \dfrac{2}{a + b} \left(ax + \int_0^1 by \, dy \right) = \dfrac{2}{a + b} \left(ax + \dfrac{b}{2} \right) = \dfrac{2ax + b}{a + b}, \quad 0 < x < 1
f_Y(y) = \int_0^1 \dfrac{2(ax + by)}{a + b} \, dx = \dfrac{2}{a + b} \int_0^1 (ax + by) \, dx = \dfrac{2}{a + b} \left( \dfrac{a}{2} + by \right) = \dfrac{a + 2by}{a + b}, \quad 0 < y < 1
6. 조건부확률분포(conditional probability distribution)
■ 조건부확률분포는 P_{X|Y}(x) = P(X = x | Y) : Y 라는 정보가 주어졌을 때, X = x 일 확률이다.
■ 확률변수 X, Y 의 결합확률분포가 f(x, y) (= P_{X, Y}(x, y) )이고,
주변확률분포가 각각 f_{X}(x) (= P_{X}(x) ), f_{Y}(y) (= P_{Y}(y) )일 때, Y 의 값이 y 로 주어지면, X 의 조건부확률분포는 f_{X | Y}(x | y) = P_{X | Y}(x | y) = \dfrac {(P(X = x, Y = y)}{P(Y = y)} = \dfrac {f_{X, Y}(x, y) (= P_{X, Y}(x, y))}{f_{Y}(y) (= P_{Y}(y))}, f_{Y}(y) (= P_{Y}(y)) > 0 이다. 반대로 X 의 값이 x 로 주어지면 f_{Y|X}(y|x) = \dfrac {f_{X|Y}(x, y)}{f_{X}(x)}, f_{X}(x) > 0 이다.
■ 즉, 조건부확률분포는 분모가 주변확률밀도함수, 분자는 결합확률밀도함수로 구성된 형태이다.
■ 예를 들어

f_{X|Y}(1 | 3) = P_{X|Y}(1 | 3) = P_{X|Y}(x = 1, y = 3) = \dfrac {P(X = 1 and Y = 3)}{P(Y = 3)} 이며, 이는 Y = 3 일 때 X = 1 일 확률을 의미한다.
- 이때, Y = 3 이라는 조건이 주어졌으므로 표본공간은 Y = 3 일 때로 축소된 것.
분모 P(Y = 3) 은 P(X = 1, Y = 3) + P(X = 2, Y = 3) + P(X = 3, Y = 3) = \dfrac{3}{20} 이다.
분자 P(X = 1 and Y = 3) = \dfrac {1}{20} 이므로 f_{X|Y}(1 | 3) = \dfrac {1}{3} 이다.
■ 연속확률변수인 경우, f_{X|Y}(x|y) = \dfrac {f_{X, Y}(x, y)}{f_{Y}(y)} 이면, P(a < X < b \mid Y = y) = \int_a^b f_{X \mid Y}(x \mid y) \, dx = \int_a^b \dfrac{f_{X, Y}(x, y)}{f_{Y}(y)} \, dx
■ 예를 들어 결합확률분포가 f(x, y) = \dfrac {2(ax + by)}{a + b}, a, b > 0, 0 < x < 1, 0 < y < 1 이면, f_{Y}(y) = \dfrac {a + 2by}{a + b} 이므로 f_{X \mid Y}(x \mid y) = \dfrac {f(x, y)}{f_{Y}(y)} = \dfrac {2(ax + by)}{a + 2by}, 0 < x < 1, 0 < y < 1 이다.
만 , Y = \dfrac {1}{2} 일 때, X 가 \dfrac {1}{2} 보다 작은 확률을 구한다면
P\left( X < \dfrac{1}{2} \mid Y = \dfrac{1}{2} \right) = \int_0^\frac{1}{2} f(X \mid Y = \dfrac{1}{2}) \, dx = \int_0^\frac{1}{2} \dfrac{2ax + b}{a + b} \, dx = \dfrac{a + 2b}{4a + 4b} 가 된다.
7. 확률변수의 독립
■ 두 사건 A, B 에 대해 P(A \cap B) = P(A) \cdot P(B) 이면 A 와 B 는 독립이었다. 즉, 확률변수 X, Y 가 서로의 확률분포에 영향을 미치지 않으면 X 와 Y 는 서로 독립이다.
■ 두 확률변수 X, Y 의 결합확률분포를 f_{X, Y}(x, y) , X 와 Y 의 주변확률분포를 f_{X}(x) , f_{Y}(y) 라 할 때, f_{X, Y}(x, y) = f_{X}(x) \cdot f_{Y}(y) , for all x, y 를 만족하면 X 와 Y 는 독립이다.
■ 예를 들어 확률변수가 이산형이면
| X = 0 | X = 1 | ||
| Y = 0 | \dfrac {3}{8} | \dfrac {3}{8} | f_{Y}(0) = \dfrac {3}{4} |
| Y = 1 | \dfrac {1}{8} | \dfrac {1}{8} | f_{Y}(1) = \dfrac {1}{4} |
| f_{X}(0) = \dfrac {1}{2} | f_{X}(1) = \dfrac {1}{2} |
1) f_{X, Y}(0, 0) = f_{X}(0) \cdot f_{Y}(0) \longleftrightarrow \dfrac{3}{8} = \dfrac{1}{2} \cdot \dfrac{3}{4}
2) f_{X, Y}(0, 1) = f_{X}(0) \cdot f_{Y}(1) \longleftrightarrow \dfrac{1}{8} = \dfrac{1}{2} \cdot \dfrac{1}{4}
3) f_{X, Y}(1, 0) = f_{X}(1) \cdot f_{Y}(0) \longleftrightarrow \dfrac{3}{8} = \dfrac{1}{2} \cdot \dfrac{3}{4}
4) f_{X, Y}(1, 1) = f_{X}(1) \cdot f_{Y}(1) \longleftrightarrow \dfrac{1}{8} = \dfrac{1}{2} \cdot \dfrac{1}{4}
모든 x, y 에 대해 f_{X, Y}(x, y) = f_{X}(x) \cdot f_{Y}(y) 를 만족하므로 확률변수 X, Y 는 모든 가능한 x, y 에 대하여 독립이라고 할 수 있다. 만약 1) ~ 4) 중 하나라도 성립하지 않으면 독립이 아니다.
■ 확률변수가 연속형인 경우, 예를 들어
f_{X, Y}(x, y) = x + y, 0 < x < 1, 0 < y < 1 이면, f_{X}(x) = x + \dfrac{1}{2}, \quad f_{Y}(y) = y + \dfrac{1}{2} 이므로, x + y \neq \left( x + \dfrac{1}{2} \right) \left( y + \dfrac{1}{2} \right) 이라서 f_{X, Y}(x, y) \neq f_{X}(x) \cdot f_{Y}(y) 이다. 따라서 독립이 아니다.
■ n 차원으로 확장하면, 확률변수 X_1, X_2, ... , X_n 의 결합확률분포를 f_{x_1, x_2, ... , x_n}(x_1, x_2, ..., x_n) 이라 할 때, X_i 의 주변확률분포는, 이산형이면 나머지 확률변수들의 영역을 더하거나, 연속형읜 경우 나머지 확률변수들의 영역을 적분하여 구할 수 있다. 만약, 확률변수 X_1, X_2, ... , X_n 이 서로 독립이면 f_{x_1, x_2, \ldots, x_n}(x_1, x_2, \ldots, x_n) = f_{X_1}(x_1) \cdot f_{X_2}(x_2) \cdots f_{X_n}(x_n) 이 성립한다.
■ 예를 들어, X_1, X_2, X_3 의 결합확률분포 f_{X_1, X_2, X_3}(x_1, x_2, x_3) = 6e^{-x_1 - 2x_2 - 3x_3} (x_1, x_2, x_3 > 0) 이면,
1) X_1 의 주변확률분포는 나머지 확률변수 X_2, X_3 의 영역에 대하여 적분하면 된다.
f_{X_1}(x_1) = \int_{0}^{\infty} \int_{0}^{\infty} 6e^{-x_1 - 2x_2 - 3x_3} \, dx_2 \, dx_3 , 이때 x_1 은 상수로 볼 수 있으므로 \int_{0}^{\infty} \int_{0}^{\infty} 6e^{-x_1 - 2x_2 - 3x_3} \, dx_2 \, dx_3 = e^{-x_1} \int_{0}^{\infty} \int_{0}^{\infty} 6e^{- 2x_2 - 3x_3} \, dx_2 \, dx_3 를 계산하면 된다.
e^{-x_1} \int_{0}^{\infty} \int_{0}^{\infty} 6e^{- 2x_2 - 3x_3} \, dx_2 \, dx_3 = 3e^{-x_1} \int_{0}^{\infty} \int_{0}^{\infty} 2e^{- 2x_2 - 3x_3} \, dx_2 \, dx_3 = e^{-x_1} \int_{0}^{\infty} 3e^{- 3x_3} \, dx_3 = e^{-x_1}, \quad (x_1 > 0)
2) X_2, X_3 의 주변확률분포도 동일한 방식으로 계산하면
f_{X_2}(x_2) = 2 \cdot e^{-2x_2} (x_2 > 0) , f_{X_3}(x_3) = 3 \cdot e^{-3x_3} (x_3 > 0) 따라서 f_{X_1, X_2, X_3}(x_1, x_2, x_3) = f_{X_1}(x_1) \cdot f_{X_2}(x_2) \cdot f_{X_3}(x_3) \longleftrightarrow 6 \cdot e^{-x_1 - 2x_2 - 3x_3} = e^{-x_1} \cdot 2 e^{-2x_2} \cdot 3 e^{-3x_3} 이 성립하므로 X_1, X_2, X_3 은 독립이라고 할 수 있다.
8. 확률변수의 변환
■ 기존에 정의된 확률변수를 이용해 새로운 확률변수를 정의해야 할 때가 있다. 이를 확률변수의 변환이라고 한다.
■ 예를 들어 동전을 10번 던져서 나오는 뒷면의 개수를 확률변수 X 라고 할 때, 뒷면 개수의 제곱만큼 1000만큼의 수익이 발생한다면, 수익이라는 새로운 확률변수 Y = 1000X^2 이 된다.
■ 위의 예시와 같이 새로운 확률변수 Y 를 기존에 정의된 확률변수 X 의 함수 형태인 Y = u(X) 로 정의한다. 따라서 Y 를 구하기 위해 확률변수 X 의 확률분포로부터 새로운 확률변수 Y = u(X) 의 확률분포를 구해야 하며, 여러 방법 중 누적분포함수법과 변수변환법이 있다.
8.1 누적분포함수법
■ 연속형 확률변수인 경우만 사용하는 누적분포함수법은 기존에 정의된 확률변수의 확률분포로부터 새로운 확률변수의 누적분포함수를 계산한 후, 이를 미분해 확률밀도함수를 구하는 방법이다.
■ 기존 확률변수 X 의 확률밀도함수를 f(x) , 새로운 확률변수 Y = u(X) 라 하면,
1) Y 의 누적분포함수 F_{Y}(y) = P(Y \leq y) 를 계산한다.
F_{Y}(y) = P(Y \leq y) = P(u(X) \leq y) = \int_{u(X) \leq y} f(x) \, dx
2) \( F_{Y}(y)\)를 미분하여 확률변수 Y 의 확률밀도함수 f_{Y}(y) 를 계산하고, 범위를 확인한다. f_{Y}(y) = \dfrac{d}{dy} F_{Y}(y)
■ 예를 들어 확률변수 X 의 확률밀도함수 f_{x} (x) = 2x, 0 \leq x \leq 1 일 때, Y = 3X - 1 의 확률분포는
1) F_{Y} (y) = P(Y \leq y) = P(3X - 1 \leq y) = P(X \leq \dfrac {y + 1}{3} , 이때 P(Y \leq y) 와 P(X \leq \dfrac {y + 1}{3} 의 면적이 같으므로 P(X \leq \dfrac {y + 1}{3}) = \int_{-\infty}^{\frac{y + 1}{3}} f(x) \, dx = \int_{0}^{\frac {y + 1}{3}} 2x \, dx = \left[ x^2 \right]_{0}^{ \frac{y + 1}{3}} = \left( \dfrac{y + 1}{3} \right)^2
2) f_{Y}(y) = \dfrac{d}{dy} F_{Y}(y) = \dfrac{d}{dy} \left( \dfrac{y + 1}{3} \right)^2 = \dfrac{2}{9} (y + 1)
3) 범위는 0 \leq X \leq 1 \rightarrow -1 \leq 3X - 1 \leq 2 \Leftrightarrow -1 \leq Y \leq 2 가 된다.
따라서 Y 의 확률밀도함수 f_{Y}(y) = \begin{cases} \dfrac{2}{9} (y + 1), & \text{} -1 \leq Y \leq 2 \\ 0, & \text{otherwise} \end{cases} 이다.
8.2 변수변환법
■ 변수변환법은 확률변수 X 와 새로운 확률변수 Y = u(X) 가 일대일 관계일 경우, 즉 함수 Y = u(X) 의 역함수 X = u^{-1}(Y) 가 존재할 때 사용할 수 있다.
■확률변수가 이산형인 경우와 연속형인 경우, 모두 사용할 수 있다. 단, 적용 방식에 차이가 있다.
■ 이산형확률변수인 경우, 다음의 식을 이용하여 새로운 확률변수 Y 의 확률분포함수를 구한다.
f_{Y}(y) = P(Y = y) = P(X = u^{-1}(y)) = f_{X}(u^{-1}(y))
■ 이산형확률변수 X 에 대해 Y = u(X) 에 일대일 변환을 하면 P(X = x) = P(Y = u(X)) 이므로, X 의 확률이 Y 의 확률과 같아진다. X 의 확률을 Y 가 이어 받는 것이라 생각하면 된다.
■ 예를 들어 확률변수 X 의 확률분포함수 f_{X}(x) = \dfrac{1}{3} \left( \dfrac{2}{3} \right)^{x^3 - 2} , x = 1, 2, 3, ... 일 때, 새로운 확률변수가 Y = X^2 이라면 X 의 값이 모두 양수이며, Y = X^2 이라 단사 함수이다. 따라서 서로 다른 양수인 X 의 각 값에 대해 유일한 Y 값이 대응되므로 확률변수 X 와 Y 는 일대일 대응이다. 그리고 y = x^2 이므로 x = \sqrt{y} . 따라서 확률변수 Y 의 확률분포는 f_{Y}\left( \sqrt{y} \right) = \dfrac{1}{3} \left( \dfrac{2}{3} \right)^{y \cdot \sqrt{y} - 2}, \quad y = 1, 4, 9, ...
■ 연속형확률변수인 경우 X 와 Y = u(X) 가 일대일 관계일 때, u 가 증가함수인지 감소함수인지 구별하여 접근해야 한다.
1) u 가 증가함수
- 증가함수는 x_1 < x_2 이면 u(x_1) < u(x_2) 이며, u 가 증가함수이면 u^{-1} 도 증가함수이다. y_1 < y_2 \quad \Rightarrow \quad U^{-1}(y_1) < U^{-1}(y_2)
- 예를 들어 y = u(x) 가 증가 함수라고 가정하면 x_1 < x_2 이면 y_1 = u(x_1) < u(x_2) = y_2 가 성립하고 역함수가 x = u^{-1}(y) 일 때, 정의역과 치역이 바뀌고 y_1 < y_2 이면 u^{-1}(y_1) = x_1 < u^{-1}(y_2) = x_2 즉, y_1 < y_2 일 때, u^{-1}(y_1) < u^{-1}(y_2) 이 성립한다.
- u(x) \leq y_1 인 x 들의 집합과 x \leq u^{-1}(y_1) 인 x 들의 집합이 동일하게 된다.

- 따라서 u 가 증가함수인 경우,
F_{Y}(y) = P(Y \leq y) = P(u(X) \leq y) = P(u^{-1}(u(X)) \leq u^{-1}(y)) = P(X \leq u^{-1}(y)) = F_{X}(u^{-1}(y)) 이므로 Y 의 누적분포함수는 F_{Y}(y) = F_{X}(u^{-1}(y)) 이다.
따라서 f_{Y}(y) = \dfrac{d}{dy} F_{Y}(y) = \dfrac{d}{dy} F_{X}(u^{-1}(y)) = f_{X}(u^{-1}(y)) \times \dfrac{d}{dy} \left( u^{-1}(y) \right) (* y 에 대한 미분이므로 속미분을 곱해줘야 한다.)
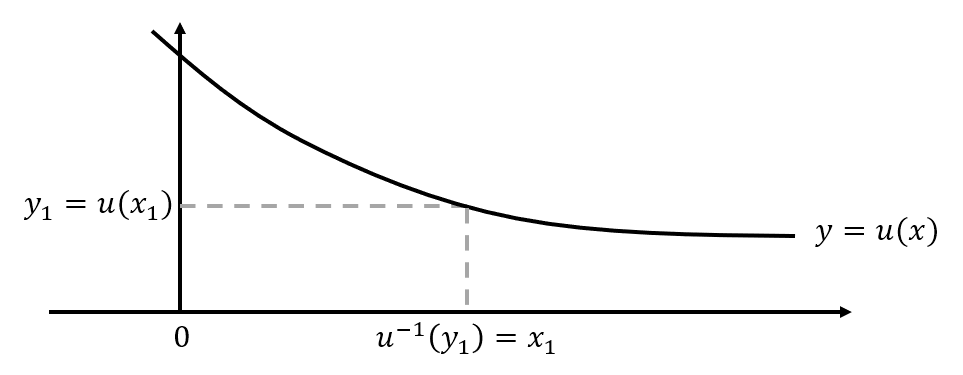
- 만약 -1 \leq X \leq 1 범위에서 Y = X^2 이었다면, Y = X^2 이 -1 \leq X \leq 1 의 구간에서 일대일 대응이 아니기 때문에 변수변환법을 적용할 수 없다.

'확률' 카테고리의 다른 글
| 연속형 확률분포 (1) (0) | 2025.02.14 |
|---|---|
| 적률생성함수 (3) | 2025.02.14 |
| 이산형 확률분포 (0) | 2025.02.14 |
| 확률변수의 기댓값과 분산, 공분산, 상관계수 (0) | 2025.02.05 |
| 확률 (0) | 2024.08.28 |



