어텐션(Attention) (1)

1. 어텐션 구조

1.1 seq2seq Encoder 개선

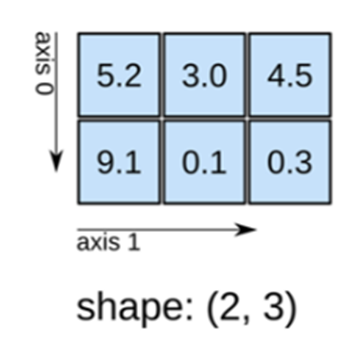
■ seq2seq는 다음 예시와 같이 Encoder가 시계열 데이터를 인코딩해서, 인코딩된 정보 $h$를 Decoder에 전달한다.

■ 이때 $h$는 고정 길이 벡터라서 입력 문장이 아무리 길어도, 항상 동일한 길이(크기)의 벡터가 된다.

■ 즉, 고정된 크기의 벡터에 모든 정보를 압축하기 때문에 문장이 길어질수록 중요한 정보가 누락될 가능성이 크다. 다시 말해, 고정 길이 벡터는 정보 손실이 발생하기 쉬운 구조이다.

■ 이 문제를 개선하는 방법으로 다음과 같이 Encoder의 모든 시점의 은닉 상태 벡터를 모두 이용하는 방법이 있다.

■ 이렇게 하면 입력된 단어와 같은 수의 벡터를 얻을 수 있다. 즉, 더 이상 Encoder 출력의 결과는 하나의 고정 길이 벡터가 아니며, 입력 문장 길이에 비례한 정보가 인코딩된다.

- $h_1, h_2, h_3, h_4$는 Encoder 모든 시점 $t = 1, 2, 3, 4$의 은닉 상태 벡터로 고정 길이 벡터

- hs는 모든 시점(각 시점의 단어)의 은닉 상태 벡터들의 집합

- hs의 원소 $h_1, h_2, h_3, h_4$는 각 시점의 단어에 대한 정보만 포함된 벡터가 된다.

 

1.2 seq2seq Decoder 개선

■ 단순한 seq2seq에서는 Encoder의 RNN(또는 LSTM) 계층의 마지막 시점의 은닉 상태를 Decoder의 LSTM 계층의 첫 은닉 상태로 설정(전달)했다.

■ 그러므로 개선한 Encoder를 사용해서 모든 시점의 은닉 상태 벡터의 집합인 hs를 단순한 Decoder에 전달하게 된다면 hs의 마지막 원소(마지막 RNN/LSTM 계층의 은닉 상태)만 Decoder에 전달된다.

(정확히는 hs의 마지막 원소만 Decoder에 전달해 Decoder의 RNN/LSTM 계층의 첫 은닉 상태로 설정)

■ 즉, 단순한 Decoder 형태를 사용하게 된다면 hs의 모든 원소(Encoder의 모든 시점의 은닉 벡터)를 활용할 수 없기 때문에 Decoder 역시 개선이 필요하다.

■ 이 개선에 사용되는 메커니즘이 바로 어텐션(attention)이다.

■ 예를 들어 '나는 학생이다'를 영어로 번역하려면 '나 = I', '학생 = student'라는 과정을 거친다. 즉, '나는 학생이다'라는 문장에 있는 단어에 주목해 '나 = I', '학생 = student'라는 대응 관계를 수시로 확인하면서 문장을 번역한다.

■ 이는 사람이 하나의 문장을 읽을 때, 어떤 한 단어의 주변 단어에도 주의를 기울이는 것과 같다. 다시 말해, 문장을 이해하기 위해 문장의 모든 단어에 어텐션을 부여하는 것이다.

■ 어텐션의 기본 아이디어는 이처럼 Decoder에서 출력 단어를 예측하는 매 시점마다, 예측해야 할 출력 단어와 대응 관계에 있는 Encoder의 입력을 다시 확인하는 것이다.

- 이때, 입출력 단어의 대응 관계를 나타내는 정보를 얼라인먼트(alignment)라고 한다.

■ 이렇게 동작하기 위해서는 Decoder의 RNN/LSTM 계층의 산출물(은닉 상태 벡터)와 개선된 Encoder의 산출물인 hs를 Decoder의 모든 시점의 Attention 계층에 연결해야 한다.

- Attention 계층을 Decoder의 Affine 계층과 LSTM 계층 사이에 위치시켰다. 단, Affine 계층 위치가 반드시 위의 그림과 같은 위치에 있어야 하는 것은 아니다.

- $h_4$는 Encoder 마지막 시점에서의 은닉 상태 벡터

■ hs를 Decoder의 모든 Attention 계층에 연결해서 매 시점마다 Decoder에 입력된 단어와 대응 관계인 단어의 벡터를 hs에서 선택하여 확인하게 한다.

- 예를 들어 Decoder가 'I'를 출력하는 시점에서는 hs에서 '나'에 대응하는 벡터를 선택해서 확인하다.

■ 주의할 점은 일반적으로 신경망의 학습은 순전파와 오차역전파를 통해 이뤄진다는 점이다.

■ 위의 그림처럼 Attention 계층이 Affine 계층과 LSTM 계층 사이에 위치하면, Decoder로부터 흘러 들어오는 손실(Loss)의 기울기는 Affine $\rightarrow$ Attention $\rightarrow$ LSTM으로 전파된다.

■ 즉, Attention 계층의 구조는 미분 가능한 연산으로 구성되어야. 즉, 끊김 없이 연속적이어야 한다. 

■ 그러므로 Attention 계층의 선택 연산은 미분 가능한 연산이어야 한다.

■ argmax같은 하나만 선택하는 연산은 이산적이 연산에 해당한다. 즉, 선택하는 연산은 미분 가능한 연산이 아니다.

■ 이 문제를 해결하기 위해 어텐션 가중치(attention weight)를 사용한다. 정확히는 모든 것을 선택하고 어텐션 가중치를 적용해 가중합(weighted sum)을 내는 방법으로 연속적인 연산을 수행ㅎ나다.

- 여기서 어텐션 가중치는 확률분포처럼 각 원소가 0.0 ~ 1.0 사이의 스칼라이며, 모든 원소의 총합은 1이다.

■ 예를 들어 다음과 같이 hs에 $h_1, h_2, h_3, h_4$가 있고, 어텐션 가중치에 가중치 $a_1, a_2, a_3, a_4$가 있다면, 각 단어가 얼마나 중요한지를 나타내기 위해 각 $h$에 대응되는 가중치 $a$를 적용한다. $a_1 \times h_1, a_2 \times h_2, a_3 \times h_3, a_4 \times h_4$

- $a$는 각 단어가 얼마나 중요한지를 나타내는 가중치

■ 그리고 가중합 $a_1 \times h_1 + a_2 \times h_2 + a_3 \times h_3 + a_4 \times h_4$을 계산해 문맥 벡터(context vector)를 생성한다.

- 문맥 벡터를 글림스(glimpse)라고 부르기도 한다.

■ 즉, 문맥 벡터는 어텐션 가중치와 인코더 상태 $(h_1, h_2, h_3, h_4)$가 연결된 값이다.

■ 여기서 $a_1 \times h_1 + a_2 \times h_2 + a_3 \times h_3 + a_4 \times h_4$처럼 모두를 선택하고 가중합을 내는 것은 연속적인 연산으로 볼 수 있다. 

- 여기서 $a_ t$는 실수이므로($t$는 시점) 아주 조금씩 값이 변할 때 결과도 부드럽게 변한다. 부드럽게 변한다는 것은 미분 가능을 의미한다. 즉, 오차역전파 과정에서 기울기를 구할 수 있다는 것이다.

- 가중치가 얼마나 커지는지(어떤 단어에 얼마나 집중하는지)가 연속적으로 변하므로, 이 변화에 따른 미분이 가능해지는 것이다. 

■ 이 예에서 만약 $h_2$가 중요한 단어라서 $a_2$의 값이 0.8이라면, 나머지 $a_1, a_3, a_4$의 총합은 0.2이므로 가중합 $a_1 \times h_1 + a_2 \times h_2 + a_3 \times h_3 + a_4 \times h_4$ 결과인 문맥 벡터에는 $h_2$의 성분이 많이 포함되어 있게 된다.

■ 즉, Decoder에 입력된 단어와 대응 관계인 단어의 벡터를 선택하는 작업을 가중합 연산이 담당하고 있는 것이다.

■ 파이썬에서 모든 것을 선택하고 가중합을 계산하는 과정은 다음과 같다.

import numpy as np

T, H = 4, 3 # T는 시계열의 길이(시점 개수), N은 은닉 상태 벡터(고정 길이 벡터)의 차원(원소 수)
hs = np.random.randn(T, H)
a = np.array([0.04, 0.8, 0.06, 0.1]) # a는 어텐션 가중치
a # h2에 대한 가중치는 0.8
```#결과#```
array([0.04, 0.8 , 0.06, 0.1 ])
````````````

ar = a.reshape(4, 1).repeat(3, axis = 1) # 4 x 1 배열의 한 축을 3번 반복 # 4 x 3, 각 열은 a의 값

ar
```#결과#```
array([[0.04, 0.04, 0.04],
       [0.8 , 0.8 , 0.8 ],
       [0.06, 0.06, 0.06],
       [0.1 , 0.1 , 0.1 ]])
````````````

hs
```#결과#```
array([[ 0.917014  ,  0.94054962, -2.08449285],
       [-0.99505169,  1.13360415,  0.4485416 ],
       [-0.91706556, -0.73644713,  0.32930899],
       [-0.77442684, -0.29026119, -0.54824708]])
````````````

t = hs * ar # 가중치 적용 # 원소별 곱 계산
t
```#결과#```
array([[ 0.03668056,  0.03762198, -0.08337971],
       [-0.79604135,  0.90688332,  0.35883328],
       [-0.05502393, -0.04418683,  0.01975854],
       [-0.07744268, -0.02902612, -0.05482471]])
````````````

## 문맥 벡터 c 계산
c = np.sum(t, axis = 0) # 가중합 # 열방향으로 sum( )
c, c.shape
```#결과#```
(array([-0.7705845 , -0.05247306,  0.49779417]), (3,))
````````````

[출처] https://velog.io/@jhdai_ly/%EB%84%98%ED%8C%8C%EC%9D%B4Numpy-%ED%8C%90%EB%8B%A4%EC%8A%A4Pandasaxis%EC%9D%98-%EC%9D%98%EB%AF%B8-%ED%96%89%EC%B6%95row%EA%B3%BC-%EC%97%B4column%EC%B6%95-axis0-axis1

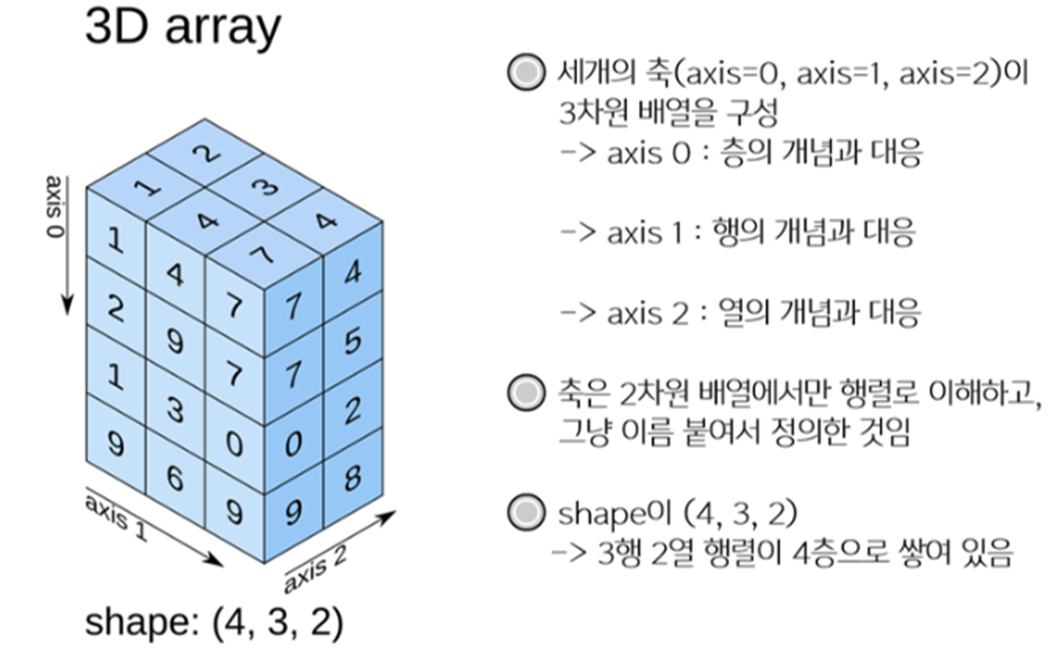
## 미니배치를 사용할 경우
N, T, H = 10, 4, 3 # N은 미니배치 수
hs = np.random.randn(N, T, H)
a = np.random.randn(N, T)
ar = a.reshape(N, T, 1).repeat(H, axis = 2) # 열 방향으로 # 열은 H개

t = hs*ar

c = np.sum(t, axis = 1) # # 가중합 # 열방향으로 sum( )

print(t.shape, c.shape)
```#결과#```
(10, 4, 3) (10, 3)
````````````

[출처] https://velog.io/@jhdai_ly/%EB%84%98%ED%8C%8C%EC%9D%B4Numpy-%ED%8C%90%EB%8B%A4%EC%8A%A4Pandasaxis%EC%9D%98-%EC%9D%98%EB%AF%B8-%ED%96%89%EC%B6%95row%EA%B3%BC-%EC%97%B4column%EC%B6%95-axis0-axis1

■ 미니배치를 사용했을 때, 가중합의 계산 그래프를 나타내면 다음과 같다.

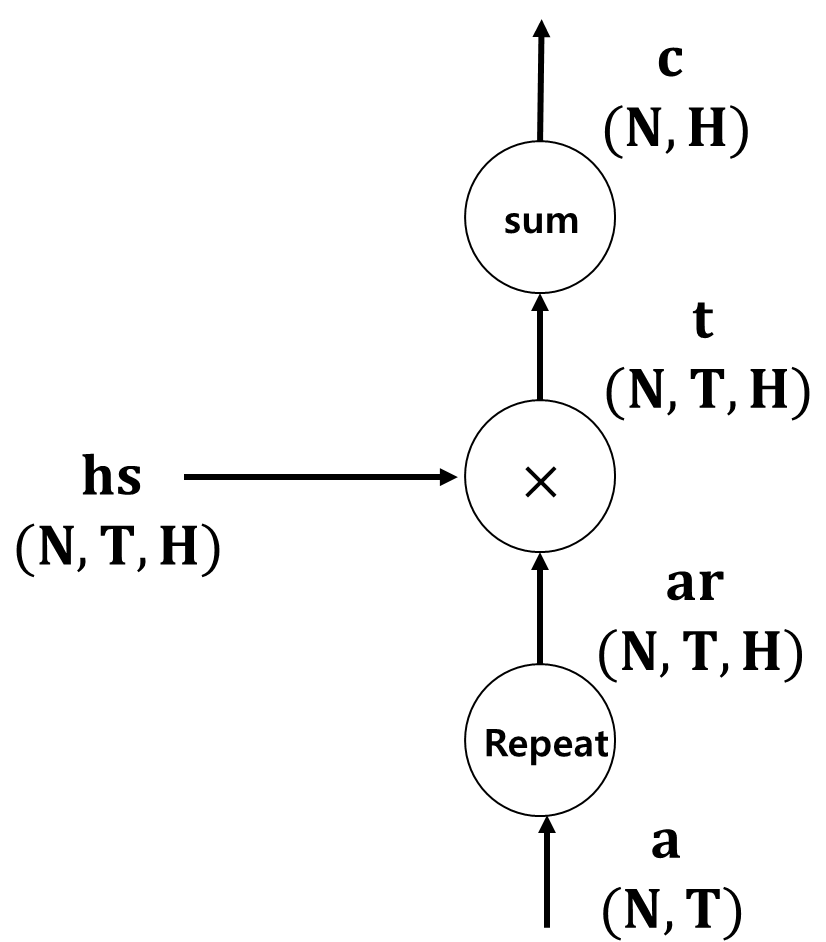
- 먼저 Repeat 노드로 $a$를 복제한다. # ar

- 그다음, hs와 원소별 곱을 계산하고 # t

- Sum 노드로 가중합을 계산한다. # c  

■ 가중합 과정 구현 https://hyeon-jae.tistory.com/157

■ 어텐션 가중치 $a$는 각 단어의 중요도를 의미하며, 데이터로부터 자동으로 학습되는 것이다.

■ $a$를 구하는 첫 번째 단계는 어텐션 스코어(attention score)를 구하는 것이다.

■ 어텐션 스코어는 현재 Decoder의 시점 $t$에서 단어를 예측하기 위해 Encoder의 hs(모든 시점의 은닉 상태)와 현재 시점 $t$의 Decoder RNN/LSTM 계층의 출력 $h_t$가 얼마나 비슷한지 수치로 나타낸 점수이다.

■ 두 벡터의 유사도(similarity)를 구하는 가장 간단한 방법은 두 벡터의 '내적'을 계산하는 것이다.

■ $\vec{a} = (a_1, a_2, \dots, a_n), \quad \vec{b} = (b_1, b_2, \dots, b_n)$이라면, $\vec{a}, \vec{b}$의 내적 $\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + \dots + a_n b_n = \vec{b}^T \vec{a}$

- 내적의 의미는 '두 벡터가 얼마나 같은 방향을 향하는가'

cf) 코사인 유사도

- $\theta = 0^\circ$, 즉 두 벡터의 사잇각이 0이며, $\text{cos}(\theta) = 1$이다. 이는 두 벡터의 방향이 완전히 동일하다는 것

- $\theta = 180^\circ$라는 건 두 벡터가 서로 반대 방향이며, $\text{cos}(\theta) = -1$ 이다. 이는 두 벡터의 방향이 $180^\circ$도 다르다는 것

- $\theta = 90^\circ$이면 $\text{cos}(\theta) = 0$

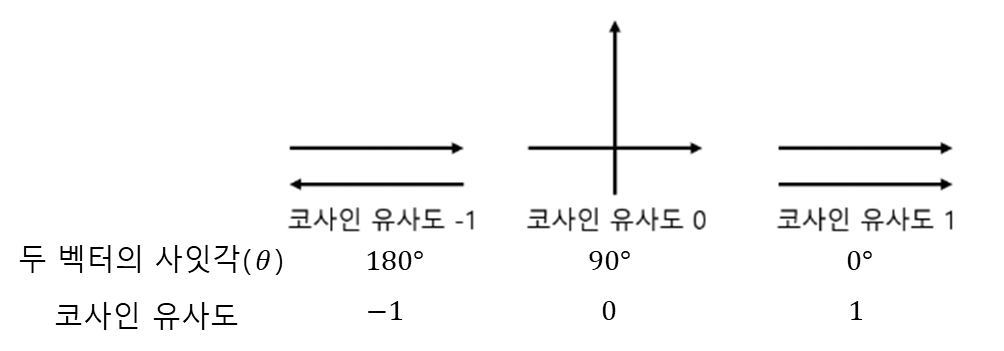
- 코사인 유사도는 -1 이상 1 이하의 값을 가지며, 1에 가까울수록 유사도가 높다고 볼 수 있다.

■ Encoder $hs$의 각 행과 Decoder $h_t$의 내적 결과를 $s$라고 하자. 

■ 다음 단계는 어텐션 스코어 $s$에 소프트맥스 함수를 적용시켜 0.0 ~ 1.0 사이의 스칼라로 정규화한다.

- 소프트맥스 함수의 결과는 원소들은 0.0 ~ 1.0 사이의 값을 가지고 모든 원소의 총합이 1이므로 확률로 해석할 수 있다.

■ 즉, 어텐션 스코어 $s$를 소프트맥스 함수로 정규화한 결과가 어텐션 가중치 $a$이다.

■ 이 과정을 계산 그래프로 나타내면 다음과 같다.

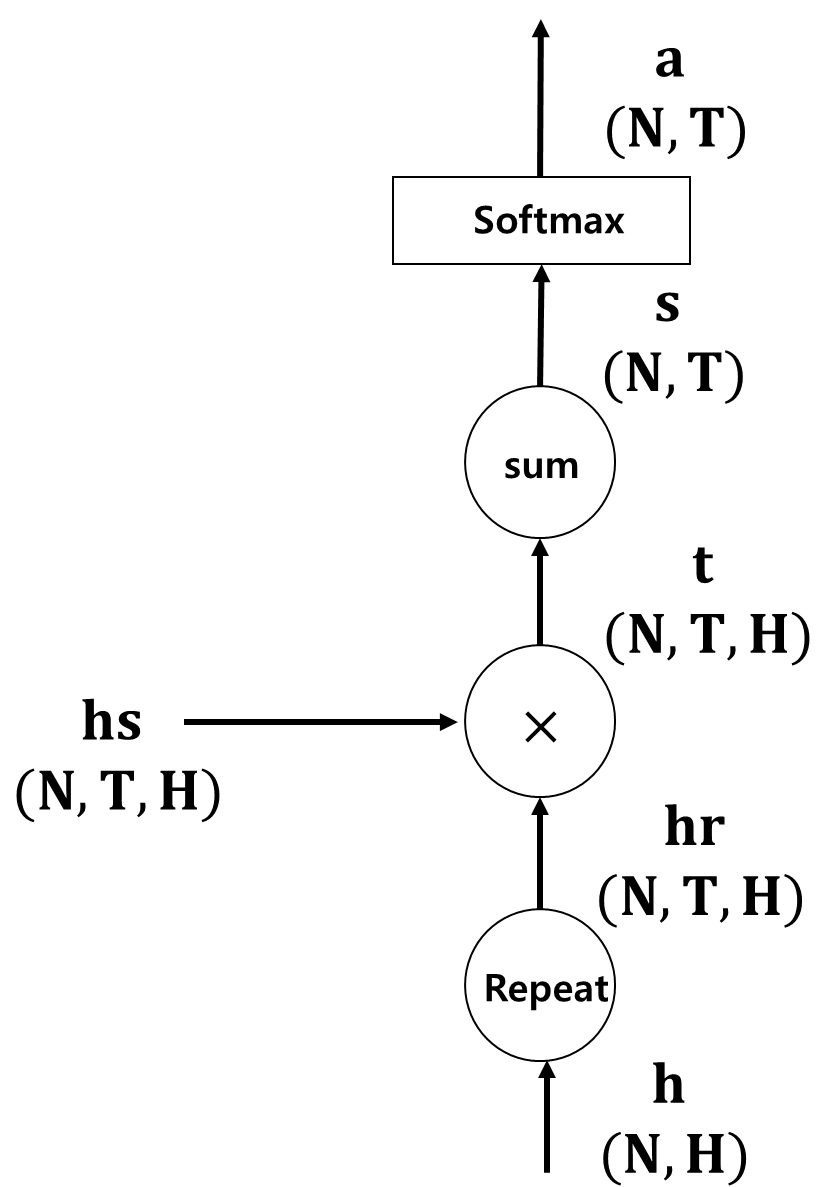
- 여기서 밑에 있는 $h$는 Decoder의 RNN/LSTM의 은닉 상태

- $s$는 어텐션 스코어, $a$는 어텐션 가중치

■ 이 과정을 (예시) 그림으로 나타내면 다음과 같다.

[출처] Introduction to Attention Mechanism - Blog by Kemal Erdem

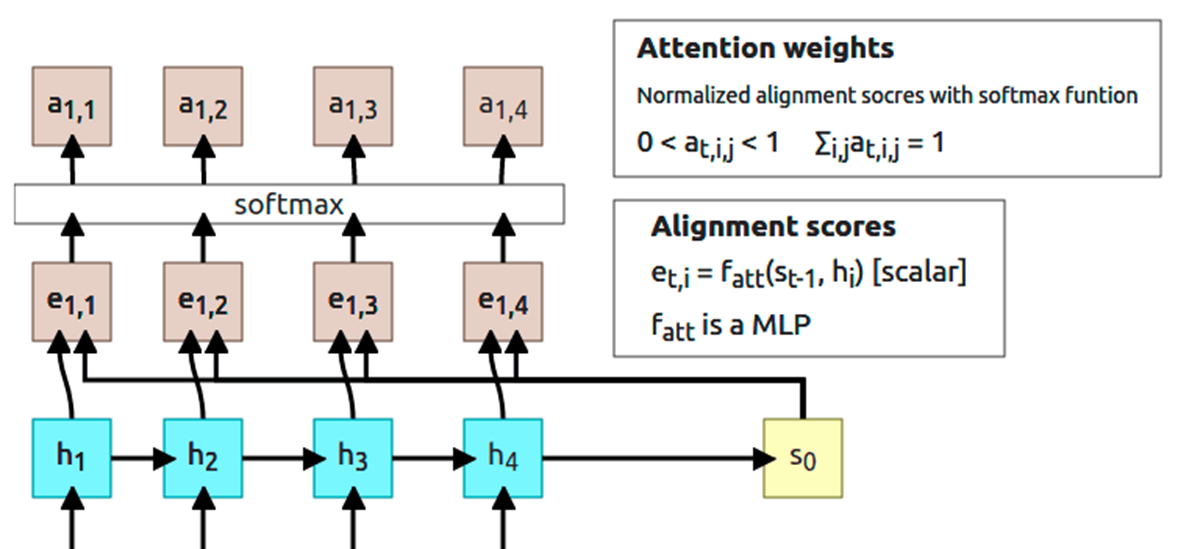
■ 어텐션 가중치 구하는 과정 구현 https://hyeon-jae.tistory.com/157

■ 지금까지의 Decoder 개선을 계산 그래프로 나타내면 다음과 같다.

■ 위의 과정을 요약하면, 개선된 Encoder가 출력한 hs(Encoder의 모든 시점의 은닉 상태 벡터)를 이용해 어텐션 스코어를 구한 다음, Softmax(attention score)를 통해 어텐션 가중치 $a$를 계산한다.

■ 그다음, 각 단어의 중요도를 나타내는 어텐션 가중치 $a$와 hs의 가중합을 통해 문맥 벡터(context vector)를 산출한다.

■ 개선된 과정, 즉 어텐션의 과정을 순서대로 나타내면 다음과 같다.

[출처] Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention) – Jay Alammar – Visualizing machine learning one concept at a time.

■ 위와 같은 일련의 계산 과정을 담당하는 계층이 바로 Attention 계층이다. 

 

2. 'seq2seq + 어텐션' 모델 구현

■ https://hyeon-jae.tistory.com/157