1. RNN의 문제점
■ RNN은 순환 경로를 통해 과거 정보를 계승할 수 있어 시퀀스 데이터(순서가 있는 데이터)인 시계열 데이터를 다루기에 적합하다.
■ 하지만, 길이가 긴 시계열 데이터를 사용할 경우 BPTT 방법으로 학습을 수행하면, 그래디언트 소실/폭발이 발생해 시간적으로 멀리 떨어진 정보를 유지하기 어렵다. 즉, 장기 기억에 취약하다.
■ RNN 계층의 순환 경로는 다음과 같으며, 시계열 데이터 \( x_t \)가 입력되면 시점 \( t \)에 대한 은닉 상태 \( h_t \)를 출력한다. 이 은닉 상태 \( h_t \)에는 과거 정보가 담겨 있다.

■ RNN 계층을 시간축으로 펼친 위의 그림을 보면, 은닉 상태 \( h_t \)는 이전 시점의 은닉 상태 \( h_{t-1} \)과 \( t \) 시점의 입력을 이용해 \( t-1 \) 시점 다음 시점인 시점 \( t \)의 은닉 상태 \( h_t \)를 계산한다.
■ RNN 구조가 이렇게 과거 정보를 순차적으로 전파하기 때문에 은닉 상태 \( h_t \)에는 \( t = 0, 1, 2, \cdots , t-1 \) 시점의 정보가 저장된다. 즉, 과거 정보를 계승할 수 있다.
■ 예를 들어 다음과 같이 \( t \) 시점의 단어를 예측하는 문제가 있을 때

■ 위의 그림처럼 마지막 계층에서 정답 레이블 t를 학습할 때,
■ 마지막 RNN 계층은 순전파 과정에서 첫 번째 RNN 계층의 은닉 상태(단어 'you'에 대한 정보가 들어 있음)부터 과거 정보가 순차적으로 전파되어, 이전 시점의 RNN 계층의 은닉 상태와 해당 시점의 입력 데이터를 이용해 단어 'to'가 들어간 시점의 Loss를 계산한다.
■ 그러므로 역전파 과정에서도 은닉 상태의 기울기가 이전 시점들의 RNN 계층으로 계속 전파된다.
■ RNN 계층을 사용한 신경망 구조는 이렇게 역전파 과정에서 각 시점의 은닉 상태 기울기가 순차적으로 전파되어 원래대로라면,
- Loss가 최소화되는 방향으로 가중치 매개변수를 업데이트해서 다음 순전파 과정에서는 더욱 올바른 단어의 출현 확률 분포가 출력되고 최종 Loss가 감소해야 하지만, (단어 간의 관계가 올바르게 학습된 상태)
- 기울기가 중간에서 소실되거나 폭발하면 가중치 매개변수가 올바르게 갱신되지 않으므로, 더 이상 각 시점의 단어 간 관계가 올바르게 학습되지 않는다.
- 서로 가까운 위치의 단어(예를 들어 'to'와 'to'이전의 단어)이면 단어 간 관계가 크게 훼손되지는 않겠지만,
- 시간적으로 멀리 떨어진 단어(예를 들어 'you'와 'to')이면, 기울기 소실 또는 폭발로 인해 관계가 크게 틀어질 것이다.
- 'you'의 은닉 상태가 \( h_0 \)라면, \( h_0 \)에 있는 정보에 대해서는 의미 없는 기울기가 전달되어 가중치 매개변수 업데이트가 제대로 일어나지 않으니, 다음 순전파 과정에서 의미 없는 \( h_0 \)가 다음 RNN 계층으로 전달되므로 성능이 떨어질 수밖에 없다.
■ RNN 계층을 사용할 경우 기울기 소실 또는 폭발이 발생하는 이유는 은닉 상태를 계산하는 식 \( h_t = \text{tanh}(h_{t-1} W_h + x_t W_x + b) \)에 있다. 더 정확히는 식에 있는 'tanh'와 '행렬 곱' 연산이 역전파 과정에서 문제가 된다.
■ \( h_t = \text{tanh}(h_{t-1} W_h + x_t W_x + b) \) 식을 이용해 각 시점의 RNN 계층에서 은닉 상태의 학습 과정을 계산 그래프 형태로 나타내면 다음과 같다.


■ 위의 그림에서 볼 수 있듯이 역전파로 전해지는 기울기 \( dh_{T-1} \)는 tanh과 행렬 곱 연산으로 통과하고 \( T-1 \) 시점에서 행렬 곱 연산을 거친 기울기가 순차적으로 이전 시점들에 전파되는 것을 볼 수 있다.
■ 이때 tanh가 기울기 소실 문제를, 행렬 곱 연산이 기울기 폭발 문제를 야기시킨다.
■ 먼저 tanh의 식은 \( y = \tanh(x) = \dfrac{e^x - e^{-x}}{e^x + e^{-x}} \)으로, 미분 값은 \( y' = 1 - \tanh^2(x) = 1 - y^2 \)이다.
■ 즉, tanh 함수는 역전파 과정에서 다음 계산 그래프와 같이 \( 1 - y^2 \) 하류에 값이 곱해진다.

■ 이 과정을 그래프로 나타내면 다음과 같다.
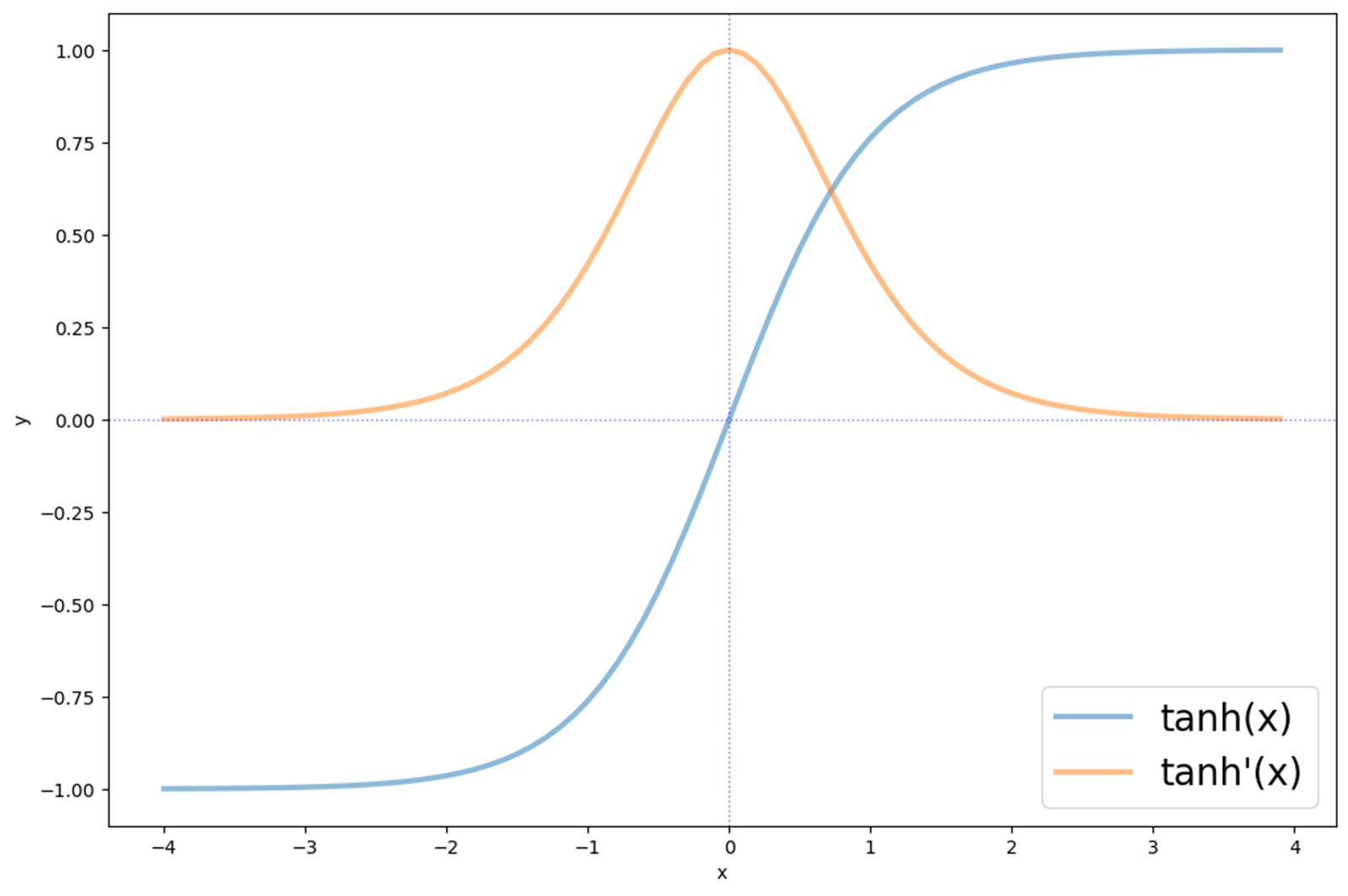
tanh(x)의 미분 그래프를 보면, \( x \) 값이 0으로부터 멀어질수록 작아져 0에 수렴하는 것을 볼 수 있다.
■ 즉, 역전파 과정에서 기울기가 tanh를 지날 때마다, 기울기 값은 계속 작아지는데, 모든 RNN 계층에서 tanh 함수를 한 번씩 사용하니, 시계열 데이터의 길이가 길어질수록 기울기 소실 문제가 발생할 가능성이 높을 수밖에 없다.
cf) 그러므로 tanh 대신, ReLU 계열의 함수를 사용한다면, 기울기 소실을 줄일 수 있을 것이다.
■ 행렬 곱 연산이 기울기 폭발 문제를 발생시키는 것도 모든 RNN 계층에서 한 번씩 행렬 곱 연산을 수행하기 때문이다.
■ 위의 은닉 상태의 학습 과정 그림에서 RNN 계층의 행렬 곱 연산 과정만 보았을 때, 순전파 과정에서 동일한 가중치 \( W_h \)가 매번 사용되므로, 역전파 과정에서 \( dh W_h^T W_h^T \cdots W_h^T \)가 전달된다.
■ 만약, 입력 데이터가 길이가 \( T \)인 시계열 데이터라면, \( W_h^T \) 값이 \( dh \)에 \( T \)번 곱해진다.
■ 그러므로 역전파 과정에서 \( W_h > 1 \)이라면 기울기 폭발, \( Wh < 1 \)이면 기울기 소실이 발생할 가능성이 높아진다.
■ 기울기 폭발 문제는 기울기 클리핑(gradients clipping)이라는 개념을 통해 해결할 수 있다.
참고) [PyTorch] Gradient clipping (그래디언트 클리핑)
[PyTorch] Gradient clipping (그래디언트 클리핑)
Gradient clipping을 하는 이유 주로 RNN계열에서 gradient vanishing이나 gradient exploding이 많이 발생하는데, gradient exploding을 방지하여 학습의 안정화를 도모하기 위해 사용하는 방법이다. Gradient clipping과 L
sanghyu.tistory.com
■ 기울기 클리핑은 기울기의 L2 노름(\( \| \widehat{g} \| \))이 특정 임곗값을 넘어가면, 다음 식과 같이 기울기에 기울기의 L2 노름으로 나눠주고 임곗값을 곱해주는 방식으로 기울기를 수정한다.

- \( \hat{g} \)는 신경망에서 사용되는 모든 매개변수의 기울기를 모은 것
- 예를 들어 신경망에서 가중치 매개변수 \( W_1, W_2 \)만 사용한다면, \( W_1, W_2 \)의 기울기 \( dW_1, dW_2 \)를 하나로 결합한 \( [dW_1, dW_2] \)가 \( \hat{g} \)
■ 기울기 클리핑을 적용하면, 다음 그림과 같이 기울기 벡터가 방향은 유지하면서 작은 값(\( \dfrac{\text{threshold}}{\| \widehat{g} \|} \widehat{g} \))만큼 이동하여(기울기 벡터의 크기를 작게 만들어) 안정적으로 내려간다.

■ 기울기 소실 문제는 '게이트(gate)'라는 구조를 더해 해결하는데, 이 게이트 구조가 더해진 대표적인 계층이 바로 LSTM(Long Short Term Memory), GRU(Gated Recurrent Units)이다.
cf) LSTM은 Long 'Short Term Memory'로 단기 기억을 장시간 유지할 수 있음을 의미한다.
cf) 게이트란? https://hyeon-jae.tistory.com/146
2. LSTM
■ LSTM의 구조는 다음 그림과 같다.

■ LSTM에는 \( c \)라는 경로가 있다. 이 \( c \)를 '기억 셀(memory cell)' 혹은 '셀'이라 하며, \( c_t \)에는 과거부터 시점 \( t \)까지의 모든 정보가 담겨 있다.
- LSTM의 기억 셀은 다른 계층에서는 보이지 않는 일종의 자신만의 추가 기억 장소이다.
- 예를 들어 위의 그림에서 \( c_t \)는 \( t \) 시점 LSTM 계층 내의 추가 기억 장소이다.
■ 이 \( c_t \)에 tanh 함수를 적용한 은닉 상태 \( h_t \)를 (\( h_t = \text{tanh}(c_t) \)를) 다음 시점의 LSTM 계층으로 전달한다. 이때 사용된 \( c_t \)는 3개의 입력 \( c_{t-1}, h_{t-1}, x_t \)로부터 계산된 결과이다.
2.1 output 게이트
■ RNN과 LSTM의 큰 차이점은 바로 게이트이다.
- RNN은 타임 스텝마다 정보의 유익성에 상관없이 은닉 상태를 업데이트한다.
- 이는 은닉 상태의 어떤 값은 유지하고, 어떤 값을 버릴지 제어하는 게이트가 없고, 순전히 은닉 상태가 입력 데이터에 의해 결정되기 때문이다.
■ \( \text{tanh}(c_t) \)로 은닉 상태 \( h_t \)를 출력하는데,
■ 여기에 게이트를 적용하면 \( \text{tanh}(c_t) \), 즉 과거부터 시점 \( t \)의 모든 정보 중 은닉 상태를 얼마나 공개할지(=중요하게 다룰지)를 \( c_t \)의 각 요소별로 판단해서 결정할 수 있다.
■ 다시 말해, 현재 시점이 \( t \)라면, \( c_t \)에서 현재 시점의 출력 \( h_t \)에 반영할 정보는 무엇인가를 한 번 거른다.
■ LSTM에는 RNN과 다르게 은닉 상태 \( h_t \)의 출력을 제어하는 output(출력) 게이트가 있다.
■ output 게이트의 열림 상태는 입력 \( x_t \)와 이전 계층의 은닉 상태 \( h_{t-1} \)를 이용해 다음과 같이 계산한다. \[ \mathbf{o} = \sigma(\mathbf{x_t} \mathbf{W}_x^{(o)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(o)} + \mathbf{b}^{(o)}) \] - \( \mathbf{W}_x^{(o)}, \mathbf{W}_h^{(o)}, \mathbf{b}^{(o)} \)는 output 게이트의 전용 매개변수
- 여기서 \( \mathbf{o} \)는 output, \( \sigma \)는 Sigmoid 함수
cf) 게이트는 열림 상태를 제어하기 위한 전용 매개변수를 이용한다. output 게이트는 output 게이트의 전용 매개변수, ... , forget 게이트는 forget 게이트의 전용 매개변수를 사용한다. 전용 가중치 매개변수는 학습 데이터로부터 갱신된다.
■ 여기서 계산된 output \( \mathbf{o} \)와 \( \text{tanh}(c_t) \)의 원소별 곱(아다마르 곱)을 통해 \( h_t \)를 출력한다. \( \mathbf{h}_t = \mathbf{o} \odot \tanh(\mathbf{c}_t) \)

■ \( \mathbf{h}_t = \mathbf{o} \odot \tanh(\mathbf{c}_t) \) 식은 다음과 같은 의미를 갖는다.
- 먼저, \( \text{tanh} \)는 출력으로 -1.0 ~ 1.0 실숫값을 가지는 함수이다.
- 그러므로 과거부터 시점 \( t \)까지의 모든 정보를 담고 있는 \( c_t \)를 \( \text{tanh} \)에 넣은 \( \text{tanh}(c_t) \)는 \( c_t \)에 인코딩된 정보의 강약 정도를 -1.0 ~ 1.0 값으로 나타낸 것
- 이 \( \text{tanh}(c_t) \)에 시그모이드 함수의 출력 값인 \( \mathbf{o} \)를 \( \text{tanh}(c_t) \)에 곱하게 되면, 어느 요소에서 어떤 비율로 정보를 꺼내고(출력하고) 차단할지 제어할 수 있다.
- 시그모이드 함수의 출력값은 0.0 ~ 1.0의 실수이기 때문에 시그모이드의 출력, 즉 output \( \mathbf{o} \) 값이 1에 가까우면 해당 요소의 \( \text{tanh}(c_t) \) 값을 거의 그대로 \( h_t \)로 보낼 것이고, 0에 가까우면 해당 요소의 정보를 거의 내보내지 않는다.
2.2 forget 게이트
■ forget(망각) 게이트는 과거 정보(\( c_{t-1} \)의 정보) 중 불필요한 정보를 버리는 역할을 한다.

■ forget 게이트도 \( x_t \)와 \( h_{t-1} \)을 이용해 다음과 같은 계산을 수행한다. \[ \mathbf{f} = \sigma(\mathbf{x_t} \mathbf{W}_x^{(f)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(f)} + \mathbf{b}^{(f)}) \] - \( \mathbf{W}_x^{(f)}, \mathbf{W}_h^{(f)}, \mathbf{b}^{(f)} \)는 forget 게이트의 전용 매개변수
■ 여기서 forget 게이트만 고려한다면, forget 게이트의 출력 \( \mathbf{f} \)와 \( c_{t-1} \)의 원소별 곱(아다마르 곱)을 통해 \( c_t \)를 출력한다. \( \mathbf{c}_t = \mathbf{f} \odot c_{t-1} \)
- 이 과정 역시, 시그모이드 함수의 출력값은 0.0 ~ 1.0이기 때문에 불필요한 정보는 0에 가까운 값으로, 해당 요소의 정보를 거의 내보내지 않는다.
2.3 새로운 기억 셀 (main 게이트)
■ LSTM에서는 이전 시점의 기억 셀 \( c_{t-1} \)에서 forget 게이트를 통해 불필요한 정보를 지운 뒤, 그 빈자리에 현재 시점에서 새롭게 발생한 정보를 보충해 넣어야 한다.
■ 그렇지 않으면 '과거에서 지워야 할 부분'만 비워진 채, 현재 시점에 필요한 정보를 반영하지 못하기 때문이다.
■ 따라서 다음과 같이 새로 기억해야 할 정보를 \( c_{t-1} \) 기억 셀에 추가해야 한다.

- 이 새로운 셀을 main 게이트라고도 한다.
■ 이 과정은 RNN에서 \( h_t \)를 계산하는 것과 동일하기 때문에 식은 다음과 같다. \[ \mathbf{g} = \tanh(\mathbf{x_t} \mathbf{W}_x^{(g)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(g)} + \mathbf{b}^{(g)}) \] - \( \mathbf{W}_x^{(g)}, \mathbf{W}_h^{(g)}, \mathbf{b}^{(g)} \)는 g 게이트의 전용 매개변수
2.4 input 게이트
■ input(입력) 게이트는 새로운 기억 셀 \( \mathbf{g} \)의 정보를 제어하는 역할을 한다. 즉, 새로운 정보를 얼마나 반영할지 결정한다.

■ input 게이트에서의 계산은 다음과 같다. \[ \mathbf{i} = \sigma(\mathbf{x_t} \mathbf{W}_x^{(i)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(i)} + \mathbf{b}^{(i)}) \] - \( \mathbf{W}_x^{(i)}, \mathbf{W}_h^{(i)}, \mathbf{b}^{(i)} \)는 input 게이트의 전용 매개변수
■ 이전 시점의 기억 셀 \( c_{t-1} \) (과거부터 시점 \( t-1 \) 까지의 모든 (인코딩된) 정보)에 forget 게이트의 출력 \( \mathbf{f} \)와 원소별 곱을 통해 \( c_{t-1} \)의 불필요한 정보는 지워진다.
- 이 결과를 \( c'_{t-1} \)이라고 하자.
■ 그다음, 새로운 기억 셀 \( \mathbf{g} \)와 input 게이트의 출력 \( \mathbf{i} \)의 원소별 곱을 통해 새로운 정보를 얼마나 반영할지가 결정된다.
■ 이 결정된 정보에 \( c'_{t-1} \)을 더해 \( c_t \)를 만들고, \( c_t \)와 output 게이트의 출력 \( \mathbf{i} \)의 원소별 곱을 통해 현재 시점의 출력(\( h_t \))가 결정된다.
■ 최종적으로 output 게이트가 다음 LSTM 계층에 전달할 \( h_t \)를 결정한다.
- 이 \( h_t \)에는 이전 시점들로부터 축적해 온 정보(장단기 정보를 포함)를 압축하여 담고 있으며, 현재 시점에 주어진 입력 정보를 반영하여, 새로운 정보도 적절히 포함한 상태이다.

■ 여기까지가 LSTM 계층 내부에서 이뤄지는 계산 과정이다.
2.5 LSTM 계층의 역전파 과정

■ 위의 LSTM 계층 역전파 과정에서 기억 셀 \( c \)의 역전파 과정만 보면, 덧셈 연산과 아다마르 곱 연산만 거쳐가는 것을 볼 수 있다.
■ 덧셈 연산은 역전파 과정에서 상류에서 전해진 기울기를 그대로 하류에 전달하기 때문에 기울기 변화는 발생하지 않는다.
■ LSTM의 게이트는 기본적으로 \( x_t \)와 \( h_{t-1} \)를 이용하기 때문에 매 시점마다 게이트 값이 달라지며, 이 게이트 값을 이용해 원소별 곱을 계산하므로, 기본적인 RNN처럼 역전파 과정에서 동일한 가중치 행렬의 행렬 곱이 누적되지 않는다.
■ 그리고 forget 게이트는 원소별 곱을 통해 역전파 과정에서 불필요한 정보에는 기울기 전파를 억제한다.
- 게이트 값 \( \mathbf{f} \)가 0에 가까운 원소는 잊기로 결정한 정보이므로, 그 부분은 기울기도 거의 흐르지 않는다.
- 반면, \( \mathbf{f} \)가 1에 가까우면 해당 부분은 기억이 유지되는 정보이므로, 기울기가 과거 방향으로 비교적 많이 전파된다. (잊기로 결정한 부분에 비해서)
■ 그러므로 기본적인 RNN과 달리 LSTM은 기억 셀의 기울기가 소실 없이 전파되어 장기 기억도 잘 유지할 수 있다.
2.6 LSTM 구현
■ https://hyeon-jae.tistory.com/147
3. GRU(Gated Recurrent Unit)
■ GRU는 LSTM의 간소화된 버전의 순환 신경망이다. LSTM의 핵심인 게이트를 사용하지만, 몇 가지 차이가 있다.
■ 먼저, LSTM은 은닉 상태와 기억 셀이라는 기억 장소를 2개 사용하는 반면, GRU는 RNN처럼 은닉 상태만 사용한다.
■ 그리고 사용하는 게이트도 GRU는 reset 게이트와 update 게이트 2개만 사용한다.
- 이에 대한 식과 구조는 다음과 같다.
\begin{align*}
\mathbf{z} &= \sigma(\mathbf{x}_t \mathbf{W}_x^{(z)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(z)} + \mathbf{b}^{(z)}) \\
\mathbf{r} &= \sigma(\mathbf{x}_t \mathbf{W}_x^{(r)} + \mathbf{h}_{t-1} \mathbf{W}_h^{(r)} + \mathbf{b}^{(r)}) \\
\tilde{\mathbf{h}} &= \tanh(\mathbf{x}_t \mathbf{W}_x + (\mathbf{r} \odot \mathbf{h}_{t-1}) \mathbf{W}_h + \mathbf{b}) \\
\mathbf{h}_t &= (1 - \mathbf{z}) \odot \mathbf{h}_{t-1} + \mathbf{z} \odot \tilde{\mathbf{h}}
\end{align*}
- LSTM처럼 \( \mathbf{r}, \mathbf{z} \) 게이트와 새로운 은닉 상태 \( \tilde{\mathbf{h}} \)는 전용 매개변수가 있다.
- '1-'노드는 \( x \)를 입력하면 \( 1-x \)를 출력한다.
■ reset 게이트는 과거 은닉 상태의 영향력을 제어하는 게이트이다.
■ \( \tilde{\mathbf{h}} \)는 새로운 은닉 상태로 식에는 reset 게이트의 \( \mathbf{r} \)과 이전 시점의 은닉 상태 \( h_{t-1} \)의 아다마르 곱이 포함되어 있다.
■ 따라서 \( \mathbf{r} = 0 \)이면 새로운 은닉 상태 \( \tilde{\mathbf{h}} \)는 과거의 은닉 상태 \( h_{t-1} \)이 완전히 무시된 상태에서 입력 데이터 \( \mathbf{x}_t \)만으로 결정된다.
■ update 게이트는 LSTM의 forget 게이트와 input 게이트의 역할을 통합한 게이트로 과거와 현재 정보의 최신화 비율을 결정한다.
- \( \mathbf{z} \)와 \( \tilde{\mathbf{h}} \)의 아다마르 곱 \( \mathbf{z} \odot \tilde{\mathbf{h}} \)은 새로 추가된 (현재 시점의) 정보의 양을 결정하고
- \( 1 - \mathbf{z} \)는 과거 은닉 상태 \( h_{t-1} \)과 아다마르 곱 \( (1 - \mathbf{z}) \odot \tilde{\mathbf{h}} \)은 과거 은닉 상태에서 삭제할 정보를 결정한다.
- 여기서 \( \mathbf{z} \odot \tilde{\mathbf{h}} \)가 input 게이트의 역할을, \( (1 - \mathbf{z}) \odot \tilde{\mathbf{h}} \)가 forget 게이트의 역할을 수행하는 것이다.
- 최종적으로, 두 계산 결과의 덧셈 연산이 다음 계층으로 전달할 \( h_t \)가 된다.
■ GRU와 LSTM 성능 차는 주어진 문제와 하이퍼파라미터 설정에 따라 달라진다. 하지만 GRU의 확실한 이점은 LSTM보다 학습할 매개변수가 적고 그만큼 계산량도 적다는 점이다.
'딥러닝' 카테고리의 다른 글
| 어텐션(Attention) (1) (0) | 2025.01.08 |
|---|---|
| 시퀀스 투 시퀀스(Sequence toSequence, seq2seq) (0) | 2025.01.07 |
| 순환 신경망(RNN) (2) (0) | 2025.01.06 |
| 순환 신경망(RNN) (1) (0) | 2025.01.06 |
| 합성곱 신경망(CNN) (2) (0) | 2024.12.06 |




