1. 오차역전파 과정
■ 어떤 입력 이미지가 순전파와 역전파를 통해 손실 함수의 값을 낮추고 최종 결과를 출력하는 과정은 다음 그림과 같다.

■ 예를 들어 입력층, 은닉층, 출력층이 각각 2개, 3개, 2개의 노드를 가진다 하자.(bias는 생략)
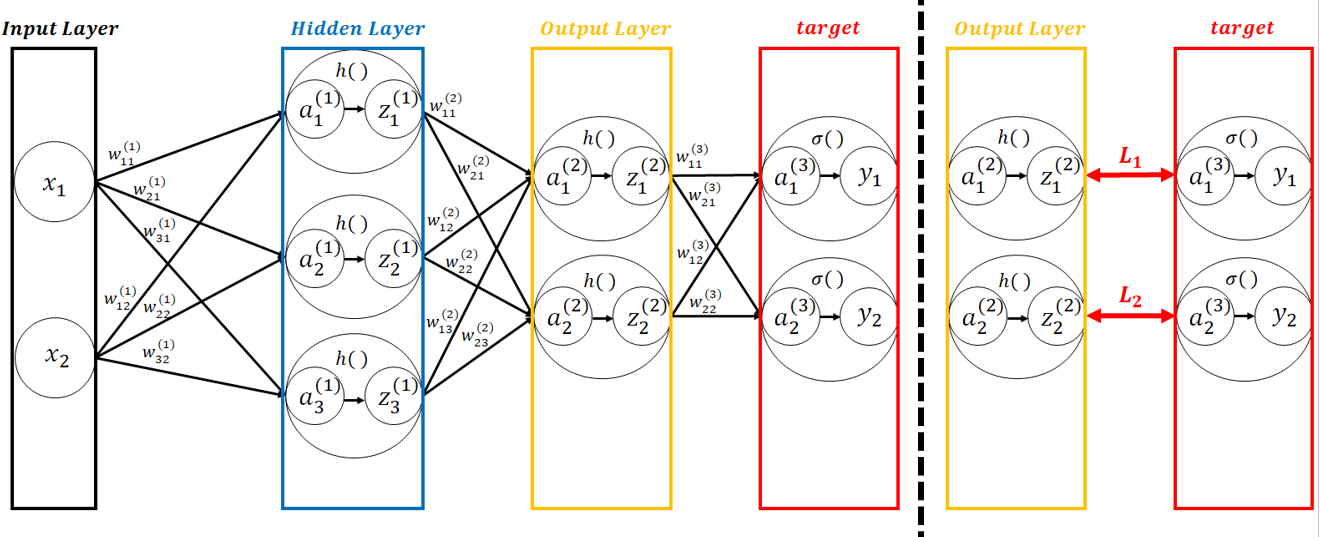
- w는 가중치이며, 선형 방정식(*bias가 있다면, wx + b)의 값, 즉 어파인 변환의 값 \( a \)를 입력 값으로 받은 활성화 함수 \( h( ) \)를 통과한 값을 \( z \), 그리고 출력층의 각 노드와 그에 대응하는 실제 값(정답)을 \( y_1, y_2 \)라 하면, \( y_1, y_2 \)와의 차이(loss)를 \( L_1, L_2 \)라 하자. 전체 손실을 \( L \)이라 하면 \( L = L_1 + L_2 \)이다.
- 가중치 업데이트는 \( w = w - \eta \times \dfrac{\partial L}{\partial w} \)이며, \(\eta\)는 사용자가 설정해야 할 학습률이다.
- Weight의 Gradient는 일반적으로 크기가 매우 크다. 따라서 이 Gradient의 크기를 조절할 필요가 있으며, 이 크기를 조절해주는 상수를 학습률이라 한다.
- 학습률은 설정하지 않으면 Gradient를 구했을 때, Loss가 제대로 감소하는 방향을 구하지 못할 확률이 높고, 아예 학습되지 않는 경우도 많다. 따라서 학습률을 적절히 설정해야 한다.
- 예를 들어 \( L_{1} = \dfrac {1}{2} (y_{1} - a_{1}^{(2)})^2 \)일 때,
\( z_{1}^{(2)} = activation(a_{1}^{(2)}) \)이고 \( a_{1}^{(2)} = w_{11}^{(2)}z_{1}^{(1)} + w_{12}^{(2)}z_{2}^{(1)} + w_{13}^{(2)}z_{3}^{(1)} \)이 된다.
- 즉, \( L_1 \)을 만드는데 관여한 가중치는 \( w_{11}^{(2)}, w_{12}^{(2)}, w_{13}^{(2)} \)임을 알 수 있다. 따라서 \( L_{1} \)은 이 가중치들을 업데이트한다.
- 기울기를 구할 때에는 연쇄 법칙(Chain Rule)이 적용되며 다음의 기울기들을 곱한다.
\[ \dfrac{\partial L_{1}}{\partial w_{1i}^{(2)}} = \dfrac{\partial L_{1}}{\partial z_{1}^{(2)}} \dfrac{\partial z_{1}^{(2)}}{\partial a_{1}^{(2)}} \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}}, \ (i = 1, 2, 3) \]
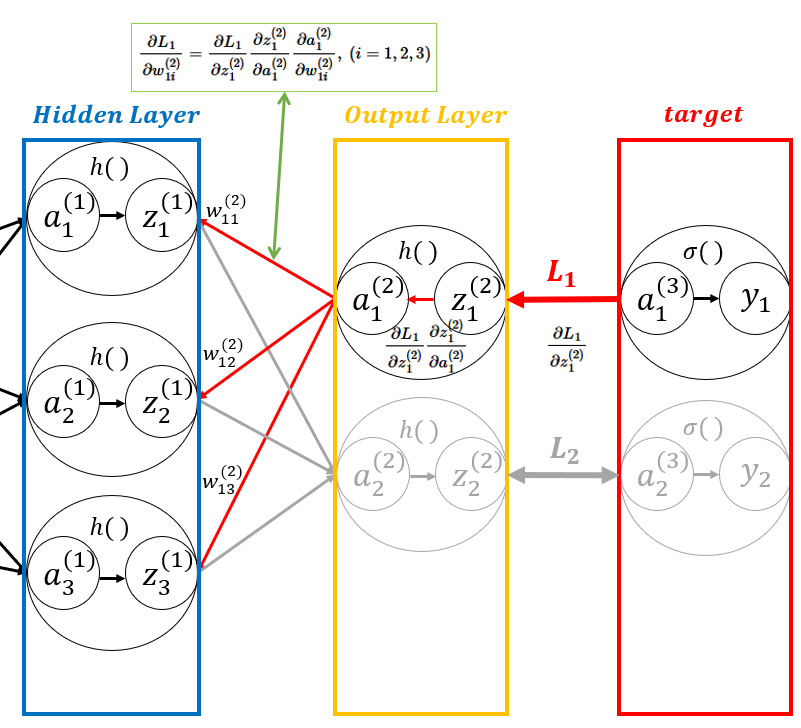
- \( \dfrac{\partial L_{1}}{\partial w_{1i}^{(2)}} = \dfrac{\partial L_{1}}{\partial z_{1}^{(2)}} \dfrac{\partial z_{1}^{(2)}}{\partial a_{1}^{(2)}} \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}}, \ (i = 1, 2, 3) \)에서 \( \beta_{1}^{(2)} = \dfrac{\partial L_{1}}{\partial z_{1}^{(2)}} \dfrac{\partial z_{1}^{(2)}}{\partial a_{1}^{(2)}} \)이라고 한다면, \( \dfrac{\partial L_{1}}{\partial w_{1i}^{(2)}} = \beta_{1}^{2} \times \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}} \)이다.
- \( \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}} \)은 \( a_{1}^{(2)} \)에 대한 \( w_{1i}^{(2)} \)의 편미분이므로,
\( a_{1}^{(2)} = w_{11}^{(2)}z_{1}^{(1)} + w_{12}^{(2)}z_{2}^{(1)} + w_{13}^{(2)}z_{3}^{(1)} \)에 \( w_{1i}^{(2)} \)의 편미분을 하면 \( \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}} = z_{1}^{(1)}, z_{2}^{(1)}, z_{3}^{(1)} \)이므로 \( \dfrac{\partial a_{1}^{(2)}}{\partial w_{1i}^{(2)}} = z_{i}^{(1)} \)로나타낼 수 있다.
- 따라서 \( \dfrac{\partial L_{1}}{\partial w_{1i}^{(2)}} = \beta_{1}^{(2)} \times z_{i}^{(1)} \)으로 표현할 수 있다.
- 가중치 업데이트는 \( w = w - \eta \times \dfrac{\partial L}{\partial w} \)이므로 \( L_{1} \)을 만드는데 관여한 가중치 업데이트는 \( \dfrac{\partial L_{1}}{\partial w_{1i}^{(2)}} = \beta_{1}^{(2)} \times z_{i}^{(1)} \)에 학습률 \( \eta \)을 곱하고 기존 가중치에서 빼준다면 가중치를 업데이트할 수 있다.
- 동일한 방법으로 오차 \( L_{2} \)도 출력층에서 입력층으로 이동하며 가중치들을 업데이트한다.
\( \dfrac{\partial L_{2}}{\partial w_{2i}^{(2)}} = \dfrac{\partial L_{2}}{\partial z_{2}^{(2)}} \dfrac{\partial z_{2}^{(2)}}{\partial a_{2}^{(2)}} \dfrac{\partial a_{2}^{(2)}}{\partial w_{2i}^{(2)}} = \beta_{2}^{(2)} \times z_{i}^{(1)}, \quad \beta_{2}^{(2)} = \dfrac{\partial L_{2}}{\partial z_{2}^{(2)}} \dfrac{\partial z_{2}^{(2)}}{\partial a_{2}^{(2)}} \), \( a_{2}^{(2)} = w_{21}^{(2)}z_{1}^{(1)} + w_{22}^{(2)}z_{2}^{(1)} + w_{23}^{(2)}z_{3}^{(1)} \)
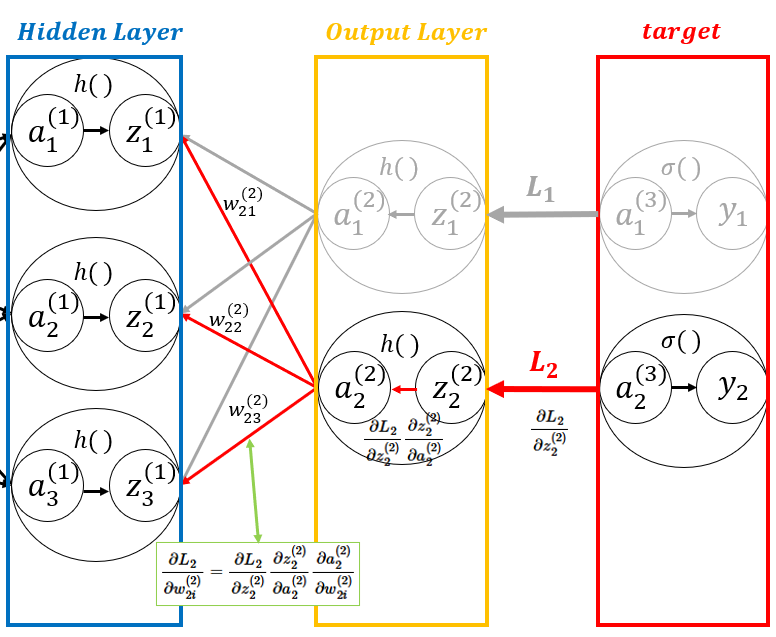
■ 다음으로 입력층과 가까운 가중치 중 먼저 \( w_{11}^{(1)} \)이 업데이트되는 과정을 보자.
■ (1) 층의 가중치인 \( w_{11}^{(1)} \)은 \( L_{1} \)과 \( L_{2} \) 오차에 모두 관여하고 있으므로 다음의 식처럼 나눠서 생각해야 한다.
- \( w_{11}^{(1)} \)에 대한 손실 함수의 기울기를 구해보면 \[ \dfrac{\partial L}{\partial w_{11}^{(1)}} = \dfrac{\partial L}{\partial z_{1}^{(1)}} \dfrac{\partial z_{1}^{(1)}}{\partial a_{1}^{(1)}} \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}} = \left( \dfrac{\partial L_{1}}{\partial z_{1}^{(1)}} + \dfrac{\partial L_{2}}{\partial z_{1}^{(1)}} \right) \dfrac{\partial z_{1}^{(1)}}{\partial a_{1}^{(1)}} \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}} \]
- 1) \( \dfrac{\partial L_{1}}{\partial z_{1}^{(1)}} = \dfrac{\partial L_{1}}{\partial z_{1}^{(2)}} \dfrac{\partial z_{1}^{(2)}}{\partial a_{1}^{(2)}} \dfrac{\partial a_{1}^{(2)}}{\partial z_{1}^{(1)}} = \beta_{1}^{(2)} w_{11}^{(2)} \), ( \( \beta_{1}^{(2)} = \dfrac{\partial L_{1}}{\partial z_{1}^{(2)}} \dfrac{\partial z_{1}^{(2)}}{\partial a_{1}^{(2)}} \) 이므로)
- 2) \( \dfrac{\partial L_{2}}{\partial z_{2}^{(2)}} = \dfrac{\partial L_{2}}{\partial z_{2}^{(2)}} \dfrac{\partial z_{2}^{(2)}}{\partial a_{2}^{(2)}} \dfrac{\partial a_{2}^{(2)}}{\partial z_{1}^{(1)}} = \beta_{2}^{(2)} w_{21}^{(2)} \), ( \( \beta_{2}^{(2)} = \dfrac{\partial L_{2}}{\partial z_{2}^{(2)}} \dfrac{\partial z_{2}^{(2)}}{\partial a_{2}^{(2)}} \) 이므로)
- 따라서 식을 정리하면, \[
\dfrac{\partial L}{\partial w_{11}^{(1)}} = \dfrac{\partial L}{\partial z_{1}^{(1)}} \dfrac{\partial z_{1}^{(1)}}{\partial a_{1}^{(1)}} \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}} = \left( \beta_{1}^{(2)} w_{11}^{(2)} + \beta_{2}^{(2)} w_{21}^{(2)} \right) \dfrac{\partial z_{1}^{(1)}}{\partial a_{1}^{(1)}} \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}}
\]
\( \beta_{11}^{(1)} = ( \beta_{1}^{(2)} w_{11}^{(2)} + \beta_{2}^{(2)} w_{21}^{(2)} ) \dfrac{\partial z_{1}^{(1)}}{\partial a_{1}^{(1)}} \)이라 하면, \( \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}} \)은 \( a_{1}^{(1)} = x_{1}w_{11}^{(1)} \)이므로 \( \dfrac{\partial a_{1}^{(1)}}{\partial w_{11}^{(1)}} = x_{1} \)이 된다.
- 따라서, \( \dfrac{\partial L}{\partial w_{11}^{(1)}} = \beta_{11}^{(1)} x_{1} \)이 되며, 마찬가지로 가중치를 업데이트 한다면, \( \text{new } w_{11}^{(1)} = w_{11}^{(1)} - \eta (\beta_{11}^{(1)} x_{1}) \)을 계산하면 된다.
■ 중요한 것은 \( \dfrac{\partial L_{1}}{\partial z_{1}^{(1)}} \)을 구할 때처럼 이미 계산되었던 값이 다시 사용된다는 것이다.
■ 즉, 역전파가 진행될 때 어떤 층에서 계산한 기울기(오차)가 다음 층에서도 사용된다. 이는 오차가 역방향으로 전파되는 것 처럼 보이며, 그림으로 나타내면 다음과 같다.

같은 층의 다른 가중치들에 대해서도 같은 방식으로 업데이트가 진행된다.
■ 예를 들어 입력 이미지의 클래스를 분류하기 위해 활성화 함수로 ReLU, 출력층 함수로 Softmax, 손실 함수로 Cross Entropy Error를 사용한다면

- softmax 앞의 Affine 계층의 출력은 정규화되지 않은 값으로, 이 값을 점수(score)라고 한다. softmax 함수는 이 점수를 입력 값으로 받아, 이 값을 정규화하여 0과 1.0 사이의 실수 값을 출력하기 때문에 출력 결과를 확률로 해석할 수 있다.
1.1 Affine 계층
■ 신경망 순전파의 흐름은 신호의 총합 \( (WX + B) \)을 차원의 원소 수가 일치하는 행렬 \( W \)와 \( X \)의 행렬 곱으로 \( Y = np.dot(X, W) + B) \)를 계산하고, 이 \( Y \)를 활성화 함수에 넣어 변환된 출력 값을 다음 층으로 전파했었다.
■ 이렇게 신경망의 순전파 과정에서 수행하는 행렬의 곱을 어파인 변환이라고 한다.
■ 행렬 곱에서 중요한 것은 다음과 같이 대응되는 차원의 원소 수를 일치시켜야 한다는 점이다.

■ 순전파 때, \( Y = np.dot(X, W) + B \)의 과정은 다음과 같다.

■ 이번에는 역전파 과정을 순서대로 보면, 먼저 '+' 노드는 상류의 값을 그대로 하류로 전달하므로 다음과 같다.

■ 역전파에서 'np.dot' 노드의 입력은 \( \dfrac{\partial L}{\partial XW} \)으로 각각 \( X \)와 \( W \)에 역전파를 계산하기 위해서는 손실 \( L \)에 대해 각각 \( X \)와 \( W \)의 변화가 \( Y \)에 미치는 영향을 계산해야 하므로 연쇄 법칙을 사용해야 한다. 이때, 주의할 점은 크기이다.
- \( Y = np.dot(X, W) \)는 다음과 같은 행렬 곱이다.
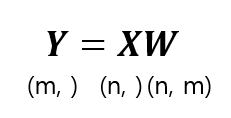
- \( X \)의 크기는 (n, )이고 \( W \)의 크기가 (n, m)일 때, \( Y \)의 차원은 \( W \)의 열의 개수에 해당하는 \( m \) 차원 벡터가 된다.
- 역전파 시, \(
\dfrac{\partial L}{\partial Y} = \dfrac{\partial L}{\partial (XW)}
\)가 상위 층에서 전달되고 이를 통해 \( X \)와 \( W \)에 대한 미분을 구해야 한다.
■ 출력으로 나온 \( Y \)의 크기는 (m, )이므로 역전파 때도 \( \dfrac{\partial L}{\partial (XW)} = \dfrac{\partial L}{\partial Y} \)는 (m, )크기의 벡터이다.

역잔파 과정의 그림을 보면 \( \dfrac{\partial L}{\partial (XW)} \cdot ? = \dfrac{\partial L}{\partial X} \), 즉 (m , ) 크기의 벡터에 어떤 크기를 곱해 (n , )인 \(
\dfrac{\partial L}{\partial X}
\)가 되야 하므로 이 \( ? \)의 크기는 (m, n)이 되야 한다.
■ 즉, 순전파 시 \( X \) (n, )에 \( W \) (n, m)을 곱해 \( Y \) (m, )를 만들었지만, 역전파 때는 반대로 입력 \( \dfrac{\partial L}{\partial (XW)} \) (m, )에 'np.dot' 노드를 거쳐 (m, n) 크기의 행렬을 곱해 출력 \( \dfrac{\partial L}{\partial X} \) (n, )을 만들어야 한다. \( W \)는 (n, m) \( ? \)는 (m, n), 즉 \( W^T \) (m, n)를 곱해줘야 한다.
■ 역전파 시, 'np.dot' 노드에서 \( W \)의 출력도 마찬가지이다.

- 순전파와 역전파 과정을 모두 정리하면 다음 그림과 같다.

■ 이를 통해 알 수 있는 것은 순전파 과정의 행렬 곱과 동일하게 역전파도 각 행렬에 대응하는 차원의 원소 수가 일치하도록 맞춰야 한다는 점이다.
■ 다만, 위와 같은 과정은 입력 데이터 \( X \)를 한 개만 고려한 경우이다. 신경망 학습은 데이터 \( N \)개를 묶어 학습을 진행하므로 데이터 \( N \)개를 묶어 학습, 즉 배치 학습 시 순전파 및 역전파를 진행하는 과정에 대해서 알아야 한다.
■ 예를 들어 입력 데이터 한 개의 크기가 (2, )라 했을 때, 이 입력 데이터를 \( N \) 개씩 묶는 경우, 입력 \( X \)의 크기는 (\( N \), 2)가 된다. 가중치 \(
W =
\begin{pmatrix}
w_{11} & w_{12} & w_{13} & w_{14} \\
w_{21} & w_{22} & w_{23} & w_{24}
\end{pmatrix}_{\scriptsize 2 \times 4}
\)
\)이라 했을 때, 입력 데이터 \( N \)개로 구성된 배치의 어파인 변화의 순전파와 역전파의 과정은 다음과 같다.
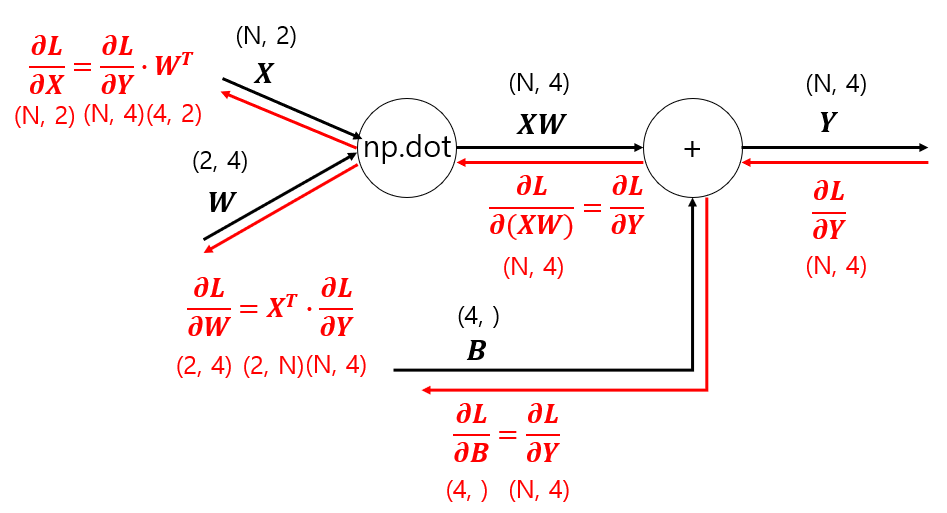
* \( \dfrac{\partial L}{\partial B} \)가 (4, ) 크기의 벡터가 되는 이유
- 순전파 때의 편향 덧셈은 \( XW \)의 행 데이터 각각에 편향이 더해진다.
- 예를 들어 \( N = 2 \)라 할때, \( X = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}_{2 \times 2} \), \( W = \begin{pmatrix} 1 & 0 & 2 & 3 \\ 0 & 1 & 3 & 2 \end{pmatrix}_{2 \times 4} \), \( B = \begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix}_{1 \times 4} \)라고 하자.
- \[
Y = X \cdot W + B = \begin{pmatrix} 1 & 2 & 8 & 7 \\ 3 & 4 & 18 & 17 \end{pmatrix} + \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{pmatrix} = \begin{pmatrix} 2 & 4 & 11 & 11 \\ 4 & 6 & 21 & 21 \end{pmatrix}
\] 이렇게 편향은 순전파 시, \( XW \)의 각 행에 더해지므로 역전파를 진행하면, 각 열의 미분 값을 합산해야 \( B \)에 대한 미분을 정확하게 계산할 수 있다.
- 예를 들어 \( \dfrac{\partial L}{\partial Y} = \begin{pmatrix} 0.1 & 0.2 & 0.3 & 0.4 \\ 0.5 & 0.6 & 0.4 & 0.1 \end{pmatrix} \)이라면 \( B \)의 \( \begin{pmatrix} 1 & 2 & 3 & 4 \end{pmatrix} \)가 순전파를 진행할 때, 각 행의 원소에 \( + \) \( \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 2 & 3 & 4 \end{pmatrix} \) 더해졌으므로 \( B \)의 각 원소에 대한 미분 값은 다음과 같이 \( \dfrac{\partial L}{\partial Y} \)의 각 열끼리 더해야 \( \dfrac{\partial L}{\partial B} = \begin{pmatrix} 0.6 & 0.8 & 0.7 & 0.5 \end{pmatrix} \) 이렇게 \( B \)에 대한 총 영향을 계산할 수 있다.
■ 파이썬에서 어파인 계층의 순전파와 역전파 과정을 나타내면 다음과 같다.
X = np.array([[1, 2], [3, 4]])
W = np.array([[1, 0, 2, 3], [0, 1, 3, 2]])
B = np.array([1, 2, 3, 4])
print(f'{X}, {X.shape}\n');print(f'{W}, {W.shape}\n');print(f'{B}, {B.shape}\n')
```#결과#```
[[1 2]
[3 4]], (2, 2)
[[1 0 2 3]
[0 1 3 2]], (2, 4)
[1 2 3 4], (4,)
`````````````
Y = np.dot(X, W) + B
print(Y, Y.shape)
```#결과#```
[[ 2 4 11 11]
[ 4 6 21 21]] (2, 4)
```````````
dY = np.array([[0.1, 0.2, 0.3, 0.4], [0.5, 0.6, 0.4, 0.1]])
print(dY, dY.shape)
```#결과#```
[[0.1 0.2 0.3 0.4]
[0.5 0.6 0.4 0.1]] (2, 4)
````````````
dB = np.sum(dY, axis = 0) # 1열, 2열,.. 열의 원소끼리 더하기 위해 행 기준으로 더함
print(dB, dB.shape)
```#결과#```
[0.6 0.8 0.7 0.5] (4,)
`````````````■ 이러한 과정을 함수로 구현하면 다음과 같다.
def AffineForward(X, W, B):
Y = np.dot(X, W) + B
return Y
def AffineBackward(X, W, B, dout):
dX = np.dot(dout, W.T)
dW = np.dot(X.T, dout)
dB = np.sum(dout, axis = 0)
return dX, dW, dB
AffineForward(X, W, B)
```#결과#```
array([[ 2, 4, 11, 11],
[ 4, 6, 21, 21]])
`````````````
AffineBackward(X, W, B, dY)
```#결과#```
(array([[1.9, 1.9],
[1.6, 2. ]]),
array([[1.6, 2. , 1.5, 0.7],
[2.2, 2.8, 2.2, 1.2]]),
array([0.6, 0.8, 0.7, 0.5]))
````````````
1.2 활성화 함수 계층
2. Softmax - Loss 계층
* 이 예에서의 Loss 계층이 Cross Entropy Error 층이라면 \( y_1, y_2, y_3 \)은 Softmax 층의 출력값, \( t_1, t_2, t_3 \)은 정답(target), \( a_1, a_2, a_3 \)은 어파인 층의 출력값, \( L \)은 손실 함수 Cross Entropy Error 층의 출력
■ 순전파 과정에서 Softmax 함수가 출력값 \( y \)를 계산하고, 이 \( y \)는 정답인 \( t \)와 함께 손실 함수 Cross Entropy Error 계층의 입력값으로 들어가서 Loss를 산출한다.
■ 역전파 과정에서는 Cross Entropy Error 계층에서 시작해, 이 계층에서 나온 역전파 결과 값이 Softmax 함수 계층의 역전파 입력이 된다. 이 과정은 다음과 같다.
2.1 Softmax 순전파
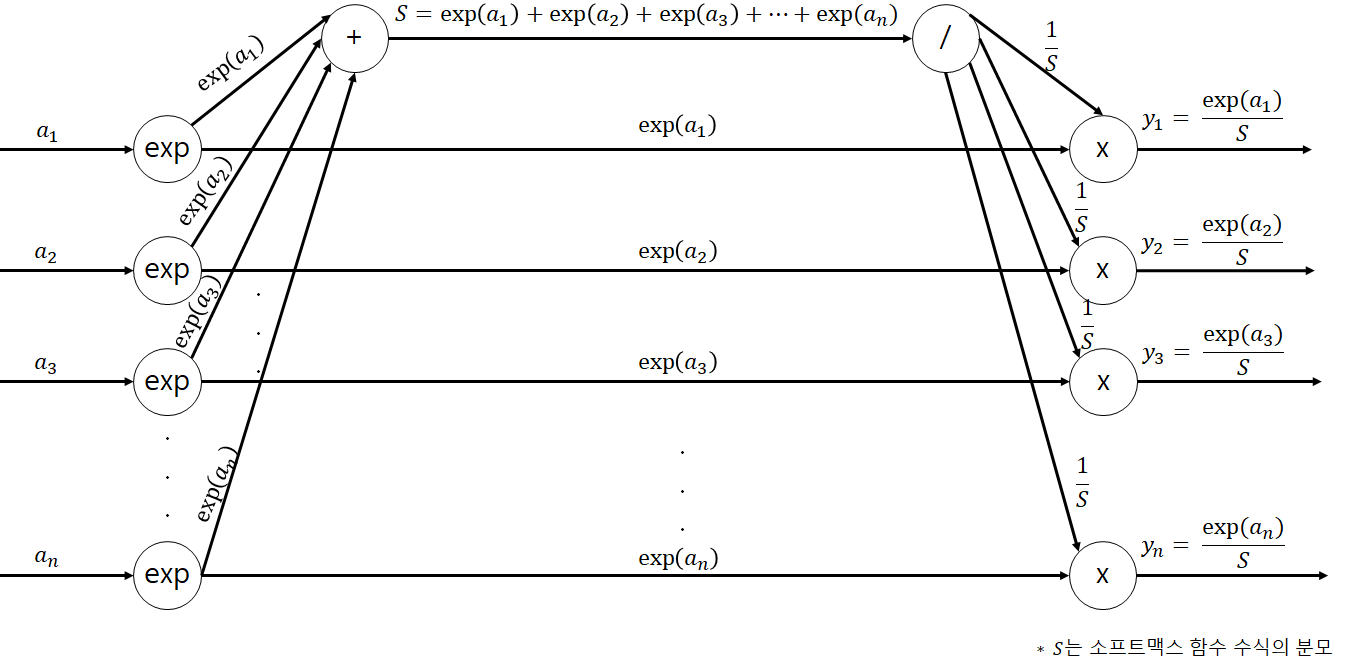
■ 소프트맥스 함수의 수식은 \( y_k = \dfrac{\exp(a_k)}{\sum\limits_{i=1}^{n} \exp(a_i)} \)이다. 수식을 순전파로 나타내면 다음과 같다.
2.2 Cross Entropy Error 순전파 & 역전파
■ Cross Entropy Error의 수식은 \( L = - \displaystyle\sum_{k} t_{k}log_{e}y_{k} \)이며, 수식을 순전파로 나타내면 다음과 같다.

■ 역전파 과정에서 주의할 점은 \( y = \log x \)는 \( \dfrac{\partial y}{\partial x} = \dfrac{1}{x} \), 즉 순전파 과정에서의 'log 노드'는 역전파 과정에서 \( \dfrac{1}{x} \), 역수를 만드는 역할을 한다.
■ 또한 역전파의 초깃값은 \( \dfrac{\partial L}{\partial L} = 1 \)이다.
■ Cross Entropy Error의 역전파는 다음과 같다.

■ 위의 그림과 같이 Cross Entropy Error 계층의 역전파 결과는 (\( -\dfrac{t_1}{y_1}, -\dfrac{t_2}{y_2}, -\dfrac{t_3}{y_3}, \ldots, -\dfrac{t_n}{y_n} \))이다. 이제 이 값이 역전파 과정에서 Softmax 계층의 입력값이 된다.
2.3 Softmax 역전파
■ 먼저 다음과 같이 Cross Entropy Error 계층의 역전파 결과 값이 Softmax 함수 계층의 역전파 입력으로 들어온다.

■ 역전파 입력값 (\( -\dfrac{t_1}{y_1}, -\dfrac{t_2}{y_2}, -\dfrac{t_3}{y_3}, \ldots, -\dfrac{t_n}{y_n} \))이 가장 먼저 만나는 노드는 'x' 노드라서 순전파의 입력들을 서로 바꿔 곱하면 \(
\left( -\dfrac{t_1}{y_1} \exp(a_1), -\dfrac{t_2}{y_2} \exp(a_2), -\dfrac{t_3}{y_3} \exp(a_3), \ldots, -\dfrac{t_n}{y_n} \exp(a_n) \right)
\)이 된다.
■ 이때 \( \left( y_1, y_2, y_3, \ldots, y_n \right) = \left( \dfrac{\exp(a_1)}{S},\ \dfrac{\exp(a_2)}{S},\ \dfrac{\exp(a_3)}{S},\ \ldots,\ \dfrac{\exp(a_n)}{S} \right) \)이므로 \(
\left(
-\frac{t_1}{y_1} \exp(a_1),\
-\frac{t_2}{y_2} \exp(a_2),\
-\frac{t_3}{y_3} \exp(a_3),\
\ldots,\
-\frac{t_n}{y_n} \exp(a_n)
\right)
=
\left(
- t_1 \frac{S}{\exp(a_1)} \exp(a_1),\
- t_2 \frac{S}{\exp(a_2)} \exp(a_2),\
- t_3 \frac{S}{\exp(a_3)} \exp(a_3),\
\ldots,\
- t_n \frac{S}{\exp(a_n)} \exp(a_n)
\right)
=
\left(
- t_1 S,\
- t_2 S,\
- t_3 S,\
\ldots,\
- t_n S
\right)
\)가 된다.

■ 위의 그림과 같이 순전파 과정에서 한 노드에서 출력 신호들이 여러 갈래로 나뉘었다면, 역전파 과정에서는 반대로 하나의 값으로 역전파 입력 신호들을 더한다.
■ 위의 그림처럼 순전파 과정에서 \( n \)개로 갈라졌다면, 역전파 과정에서 \( - t_1 S - t_2 S - t_3 S - \ldots - t_n S = S \left( - t_1 - t_2 - t_3 - \ldots - t_n \right) \)으로 합쳐져서 '/' 노드의 역전파 입력으로 들어간다.
■ 이때 '/' 노드의 역전파는 역전파의 입력으로 들어온 값에 순전파 때의 출력을 제곱한 후, 마이너스를 붙인 값을 곱해서 전달한다. 순전파 때 '/' 노드의 출력은 \( \dfrac{1}{S} \)이므로 역전파 때 \( - \dfrac{1}{S^2} \)을 \( S( - t_1 - t_2 - t_3 - \ldots - t_n) \)에 곱하여 \(\dfrac{1}{S} \left( t_1 + t_2 + t_3 + \ldots + t_n \right)\) 값을 출력한다.
■ 만약, 정답 레이블 \( \left( t_1, t_2, \ldots, t_n \right) \)에 원핫 인코딩이 적용되었다면 \( t_1 + t_2 + t_3 + \ldots + t_n = 1 \)이 된다. 즉, \(\dfrac{1}{S} \left( t_1 + t_2 + t_3 + \ldots + t_n \right) = \dfrac{1}{S}\)이 된다.

■ 그리고 순전파 과정에서 exp 노드로부터 출력된 \( \exp(a_1), \exp(a_2), \ldots, \exp(a_n) \)는 역전파 과정에서 \( \left( -\dfrac{t_1}{y_1} \dfrac{1}{S}, -\dfrac{t_2}{y_2} \dfrac{1}{S}, -\dfrac{t_3}{y_3} \dfrac{1}{S}, \ldots, -\dfrac{t_n}{y_n} \dfrac{1}{S} \right) \)이 되고 \( \left( y_1, y_2, y_3, \ldots, y_n \right) = \left( \dfrac{\exp(a_1)}{S}, \dfrac{\exp(a_2)}{S}, \dfrac{\exp(a_3)}{S}, \ldots, \dfrac{\exp(a_n)}{S} \right) \)이므로 \(\left( -\dfrac{t_1}{y_1} \dfrac{1}{S}, -\dfrac{t_2}{y_2} \dfrac{1}{S}, -\dfrac{t_3}{y_3} \dfrac{1}{S}, \ldots, -\dfrac{t_n}{y_n} \dfrac{1}{S} \right) = \left( - \dfrac{t_1}{\exp(a_1)}, - \dfrac{t_2}{\exp(a_2)}, - \dfrac{t_3}{\exp(a_3)}, \ldots, - \dfrac{t_n}{\exp(a_n)} \right) \)가 된다.

■ 최종적으로 exp 노드의 역전파 입력으로 \( \dfrac{1}{S} \)과 \( \left( \dfrac{1}{S} - \dfrac{t_1}{\exp(a_1)}, \dfrac{1}{S} - \dfrac{t_2}{\exp(a_2)}, \ldots, \dfrac{1}{S} - \dfrac{t_n}{\exp(a_n)} \right) \)가 되며
■ \( y = e^x \)는 \( \dfrac{\partial y}{\partial x} = e^x = \exp(x) \)이므로 역전파 입력으로 전달된 값 \( \left( \dfrac{1}{S} - \dfrac{t_1}{\exp(a_1)}, \dfrac{1}{S} - \dfrac{t_2}{\exp(a_2)}, \ldots, \dfrac{1}{S} - \dfrac{t_n}{\exp(a_n)} \right) \)에 \( \exp(a_{i = 1, 2, \ldots, n}) \)이 곱해져서 \( \left( \left( \dfrac{1}{S} - \dfrac{t_1}{\exp(a_1)} \right) \exp(a_1), \left( \dfrac{1}{S} - \dfrac{t_2}{\exp(a_2)} \right) \exp(a_2), \ldots, \left( \dfrac{1}{S} - \dfrac{t_n}{\exp(a_n)} \right) \exp(a_n) \right) \)이 된다.
■ 마찬가지로 \( \left( y_1, y_2, \ldots, y_n \right) = \left( \dfrac{\exp(a_1)}{S}, \dfrac{\exp(a_2)}{S}, \ldots, \dfrac{\exp(a_n)}{S} \right) \)이므로 \( \left( \left( \dfrac{1}{S} - \dfrac{t_1}{\exp(a_1)} \right) \exp(a_1), \left( \dfrac{1}{S} - \dfrac{t_2}{\exp(a_2)} \right) \exp(a_2), \ldots, \left( \dfrac{1}{S} - \dfrac{t_n}{\exp(a_n)} \right) \exp(a_n) \right) = \left( y_1 - t_1, y_2 - t_2, \ldots, y_n - t_n \right) \)이 Softmax 함수 역전파 결과 값으로 출력되어, 다시 다음 계층의 역전파 입력으로 전달된다.
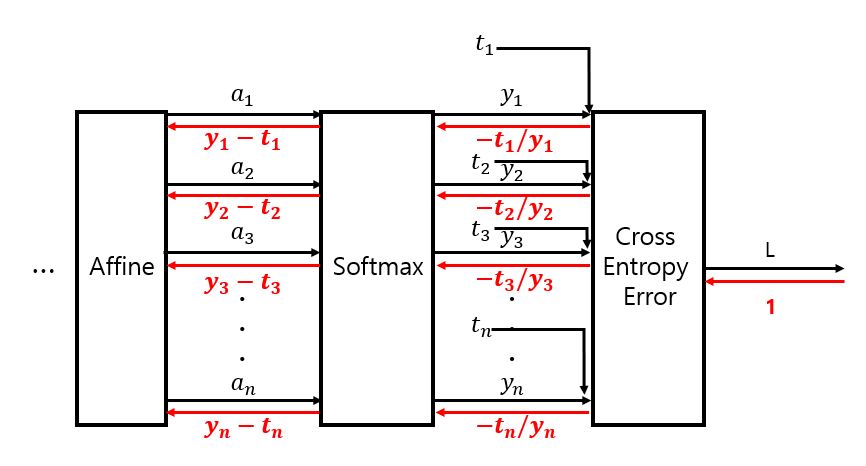
■ 이를 통해 알 수 있는 것은 순전파 과정에서 어파인 계층과 활성화 함수 계층을 통해 Softmax 함수의 입력으로 들어온 \( a_1, a_2, \ldots, a_n \)은 Cross Entropy Error 계층에서 \( Loss \)를 산출하고, 역전파 과정에서 \( Loss \)는 다시 Cross Entropy Error 계층을 거쳐 Softmax 함수 계층에서 \( y_1 - t_1, y_2 - t_2, \ldots, y_n - t_n \)으로 출력되어 다음 계층의 역전파 입력으로 전달된다는 점이다.
■ \( y_1 - t_1, y_2 - t_2, \ldots, y_n - t_n \)은 신경망의 출력값과 실제 정답과의 오차를 의미하고, 이 값을 기준으로 매개변수를 조절하여, 다시 순전파 과정을 진행한다. 만약, 손실 함수 값 \( Loss \)가 더 감소될 수 있다면 다시 역전파를 진행하고, 이 과정을 \( Loss \)가 최솟값이 될 때까지 반복한다.
- 예를 들어, 정답 \( t = (0, 0, 1, 0) \)일 때, 순전파 과정에서 소프트맥스 계층에서 이미지를 제대로 인식하지 못해 \( y = (0.1, 0.5, 0.3, 0.1) \)를 출력했다면, 역전파 과정에서 소프트맥스 계층의 역전파는 \( 0.1 - 0, 0.5 - 0, 0.3 - 1, 0.1 - 0) = (0.1, 0.5, -0.7, 0.1) \)라는 큰 오차를 전파하게 된다.
- 반대로 소프트맥스 계층에서 \( y = (0, 0.01, 0.99, 0) \)를 출력했다면, 소프트맥스 함수 계층의 역전파가 보내는 오차는 \(0, 0.01, -0.01, 0) \)이라는 작은 오차를 소프트맥스 계층의 앞 계층으로 전파하게 되고, 전파된 오차가 작으므로 학습하는 정도도 작아진다.
■ 이를 파이썬으로 구현하려면,
- forward에는 소프트맥스 함수에 입력값을 넣어 소프트맥스 함수의 출력값 \( y \)를 계산하고, 계산된 \( y \) 값을 교차 엔트로피 오차 함수에 입력값으로 넣어 \( Loss \)를 출력하면 된다.
- backward의 경우 초깃값은 \(\dfrac{\partial L}{\partial L} = 1 \)이며, 역전파 결과로 \( y - t \)의 값을 출력하면 된다. 이때, 역전파하는 값을 배치 크기로 나눠서 하나의 데이터 당 오차를 앞 계층으로 전달한다.
def forward(x, t):
y = softmax_function(x)
loss = cross_entropy_error(y, t)
# print(f'y: {y}\n'); print(f'Loss: {loss}')
return loss
def backward(y, t, dout = 1):
dx = (y - t)
return dxx1 = np.array([0, np.log(5), np.log(3), 0])
x2 = np.array([-1000, -4.595, 0, -1000])
t = np.array([0, 0, 1, 0])
forward(x1, t)
```#결과#```
y: [0.1 0.5 0.3 0.1]
Loss: 1.203972804325936
1.203972804325936
````````````
forward(x2, t)
```#결과#```
y: [0. 0.01000119 0.98999881 0. ]
Loss: 0.010051534425952286
0.010051534425952286
`````````````
y1 = np.array([0.1, 0.5, 0.3, 0.1])
y2 = np.array([0., 0.01000119, 0.98999881, 0. ])
backward(y1, t)
```#결과#```
array([ 0.1, 0.5, -0.7, 0.1])
````````````
backward(y2, t)
```#결과#```
array([ 0. , 0.01000119, -0.01000119, 0. ])
````````````■ 만약 배치 사이즈를 고려한다면
def backward2(y, t, dout = 1):
batch_size = t.shape[0]
dx = (y - t) / batch_size
return dx
backward2(y1, t)
```#결과#```
array([ 0.025, 0.125, -0.175, 0.025])
````````````
backward2(y2, t)
```#결과#```
array([ 0. , 0.0025003, -0.0025003, 0. ])
````````````'딥러닝' 카테고리의 다른 글
| 매개변수 갱신 방법(1) (0) | 2024.11.01 |
|---|---|
| 합성곱 신경망(CNN) (1) (0) | 2024.11.01 |
| 신경망 학습(2) (0) | 2024.09.13 |
| 신경망 학습(1) (1) | 2024.09.12 |
| 신경망 (2) (0) | 2024.09.05 |



