1. 정렬이란?
■ 데이터를 저장하기 위해 복잡한 자료구조를 사용하는 주된 이유는 효율적인 탐색(searching)과 정렬(sorting)을 위해서이다.
■ 정렬은 데이터를 '순서'대로 재배열하는 것이므로 비교할 수 있는 모든 속성들은 정렬의 기준(키, 정렬 키)이 될 수 있으며 '순서'에는 오름차순과 내림차순이 있다.
■ 이 오름차순과 내림차순이 정렬 키를 기준으로 순서를 정렬하는 방법이 된다.
■ 정렬시킬 대상을 레코드(record)라고 하며, 레코드는 여러 개의 필드(field)로 이루어진다.
■ 예를 들어 고객 정보에는 고객 ID, 이름, 나이, 키, 주소, 주문 금액 등의 여러 가지 속성들이 있는데, 이 속성들이 필드가 되며, 필드 중 정렬의 기준이 되는 필드를 키(key) 또는 정렬 키(sort key)라고 한다.
■ 정렬이란 정렬시켜야 될 대상인 레코드들을 정렬 키의 순서로 재배열하는 것이다.
2. 정렬 종류
■ 구현이 단순하지만 알고리즘 효율성이 비효율적인 방법으로 삽입 정렬, 선택 정렬, 버블 정렬 등이 있고
■ 반대로, 구현이 복잡하지만 효율적인 방법으로 병합 정렬, 퀵 정렬, 힙 정렬, 기수 정렬 등이 있다.
■ 보통 전자의 방법들을 기본 정렬 알고리즘, 후자의 방법들을 고급 정렬 알고리즘이라 한다.
■ 이때, 안정성(stability)을 충족하는 정렬으로 삽입 정렬, 버블 정렬, 병합 정렬 등이 있다.
■ 안정성은 데이터에 동일한 키 값을 갖는 레코드가 여러 개일 때, 정렬 후에도 이들의 위치가 바뀌지 않는 것을 의미한다.
3. 기본 정렬 알고리즘
3.1 선택 정렬(Selection Sort)
■ 선택 정렬은 초기에는 정렬되지 않은 오른쪽 리스트에서 가장 작은 숫자를 선택하여, 빈 왼쪽 리스트의 맨 뒤로 옮기는 작업을 오른쪽 리스트가 빈 리스트가 될 때까지 반복해서 왼쪽 리스트에는 정렬된 내용이 저장되게 하는 방법이다.
■ 이 방법은 단순히 작은 숫자부터 순서대로 옮기는 단순한 방식이지만, 새로운 리스트(왼쪽 리스트)를 만들어야 한다.
■ 즉, 추가적인 리스트가 필요하며 그만큼의 메모리가 추가적으로 필요한 비효율적인 방법이다.
■ 단, 원래 주어진 리스트 내부에서 정렬하는 방식인 인라인(in line = in - place) 방식으로 선택 정렬을 구현할 경우, 새로운 리스트 없이 정렬을 할 수 있다.
■ 이 방식은 먼저 정렬이 안 된 리스트에서 최솟값을 찾고, 최솟값과 리스트의 첫 번째 항목과 자리 교환, 그리고 위치를 교환하지 않은 항목들 중에서 최솟값을 찾고 두 번째 항목과 자리 교환, ...
■ 이 과정을 반복하면 정렬된 부분과 정렬되지 않은 부분으로 나뉘게 된다. 만약, 전체 항목의 개수가 n개 라면 이 과정을 n−1번 반복했을 때, 전체 리스트가 정렬된다.
■ 예를 들어 [2,2∗,1,3]에 선택 정렬을 적용하면 (2∗=2)
- 1) 먼저, 최솟값 1과 첫 번째 항목 2가 자리를 교환한다. [1,2∗,2,3]
- 2) 두 번째 과정에서 최솟값 2는 이미 정렬되어 있어 다른 항목과 교환하지 않는다.
- 3) 세 번째 과정에서 최솟값 2도 이미 정렬되어 있어 다른 항목과 교환하지 않는다.
- 이 예에서 2는 2∗앞에 있었지만, 선택 정렬 후 2가 2∗보다 뒤로 배치되면서 순서가 바뀌었다.
- 이렇게 선택 정렬은 불안정 정렬로서 안정성을 충족하지 않는 경우가 있다.
3.1.1 선택 정렬 구현
■ 선택 정렬은 항목의 개수가 n개 일 때, n−1번의 반복 과정에서 최솟값을 찾고 첫 번째 위치의 항목부터 최솟값과 위치를 교환하면서 전체 배열을 정렬된 부분과 정렬되지 않은 부분으로 나누면서 정렬하는 방법이다.
■ 따라서 구현에는 최솟값의 인덱스를 찾는 과정과 최솟값의 위치를 순서대로 교환하는 과정이 필요하다.
def SelectionSort(lst):
# print(f'초기 상태 {lst}\n')
n = len(lst)
for i in range(n-1): # n-1 번 반복
least = i # i = 0이면 least = 0
for j in range(i+1, n):
if lst[j] < lst[least]: # 인덱스 1번 항목 < 인덱스 0번 항목이면
least = j # least = 1로 갱신해서
lst[i], lst[least] = lst[least], lst[i] # 인덱스 0번 항목은 인덱스 1번 항목의 값으로,
# 인덱스 1번 항목은 0번 항목의 값으로 바꾼다
# print(f'{i+1} 번째 {lst}\n')lst = [5, 3, 8, 4, 9, 1]
SelectionSort(lst)
```#결과#```
초기 상태 [5, 3, 8, 4, 9, 1] # 최솟값 1을 첫 번째 항목 5와 위치 교환
1 번째 [1, 3, 8, 4, 9, 5] # 최솟값 3이 두 번째 항목에 있으므로 위치 교환 발생 x
2 번째 [1, 3, 8, 4, 9, 5] # 최솟값 4를 세 번째 항목 8과 위치 교환
3 번째 [1, 3, 4, 8, 9, 5] # 최솟값 5를 네 번째 항목 8과 위치 교환
4 번째 [1, 3, 4, 5, 9, 8] # 최솟값 8을 다섯 번째 항목 9와 위치 교환
5 번째 [1, 3, 4, 5, 8, 9] # 마지막 9가 마지막 항목에 있으므로 위치 교환 발생 x
``````````````■ 선택 정렬은 다음과 같이 이중 루프로 구성되며,
for i in range(n-1):
...
for j in range(i+1, n):외부 루프에서 i = 0일 때, 내부 루프 j는 1부터 n - 1까지 → n - 1번 비교
i = 1일 때, j는 2부터 n - 1까지 → n - 2번 비교
i = 2일 때, j는 3부터 n - 1까지 → n - 3번 비교
...
i = n - 3일 때, j는 n - 2부터 n - 1까지 (n -1) - (n - 2) + 1 = 2번 비교
마지막 i = n - 2일 때, (n - 1) - (n -1) + 1 = 1번 비교이므로
전체 비교 횟수는 (n−1)+(n−2)+(n−3)+...+2+1=n(n−1)2이므로 선택 정렬의 시간 복잡도는 O(n2)이 된다.
■ 이렇게 선택 정렬은 안정성을 충족하지 않고 시간 복잡도도 O(n2)으로 효율과 거리가 멀지만, 자리 이동 횟수가 input의 길이 n에 따라 미리 결정되고 알고리즘 구현이 간단하다는 장점이 있다.
3.2 삽입 정렬(Insertion Sort)
■ 삽입 정렬은 정렬된 부분에 새로운 항목을 올바른 위치에 삽입하는 과정을 정렬되지 않은 항목이 하나도 없을 때까지 반복하는 방법이다.
■ 예를 들어 [5, 3, 8, 4, 9, 1]에 삽입 정렬을 적용하면

3.2.1 삽입 정렬의 구현
■ 삽입 정렬은 위의 예시와 같이 두 번째 항목부터 정렬된 부분에 삽입할 위치를 찾고, 올바른 위치에 삽입 시 한 칸씩 뒤쪽으로 이동이 필요한 경우가 있다.
def InsertionSort(lst):
# print(f'초기 상태 {lst}\n')
n = len(lst)
for i in range(1, n): # 첫 번째 항목(인덱스 0)은 이미 정렬된 상태라 가정, 두 번째 항목부터 정렬 시작
key = lst[i] # 현재 삽입할 원소
j = i-1 # 삽입할 원소의 바로 앞의 위치
while True:
if j < 0 or lst[j] <= key: # j가 음수가 되어 리스트를 벗어나거나 올바르게 정렬된 상태라면
break # break
lst[j+1] = lst[j] # key 값을 삽입할 자리를 만들기 위해 기존 원소들을 한 칸씩 뒤로
j -= 1
lst[j+1] = key # j+1 앞 자리에 삽입
# print(f'{i} 번째 {lst}\n')lst = [5, 3, 8, 4, 9, 1]
InsertionSort(lst)
```#결과#```
초기 상태 [5, 3, 8, 4, 9, 1]
1 번째 [3, 5, 8, 4, 9, 1]
2 번째 [3, 5, 8, 4, 9, 1]
3 번째 [3, 4, 5, 8, 9, 1]
4 번째 [3, 4, 5, 8, 9, 1]
5 번째 [1, 3, 4, 5, 8, 9]
`````````````■ 삽입 정렬은 첫 번째 항목은 이미 정렬된 부분으로 간주하고, 두 번째 항목부터 올바른 위치를 찾아간다. 즉, 이미 자료가 정렬되어 있으면 있을수록 연산 시간이 단축된다.
■ 따라서 삽입 정렬의 시간 복잡도는 입력 자료의 구성에 따라 달라진다.
- 최선의 경우(best)는 이미 모든 입력 자료가 정렬되어 있는 상태이고,
- 최악의 경우(worst)는 입력 자료가 역으로 정렬되어 있는 경우이기 때문이다.
■ 이미 자료가 정렬되어 있는 경우 외부 루프에서 n−1번 실행되고 while 문은 n−1번 동안 계속 break를 수행하므로 최선의 경우 if 문의 비교 연산 lst[j] <= key가 n−1번 실행되고 원소들을 한 칸씩 뒤로 밀어 내는 이동 연산은 발생하지 않으므로 시간 복잡도는 O(n)이다.
■ 그러나 최악의 경우는 [5, 4, 3, 2, 1], 이런 식으로 역순으로 정렬되어 있어
[5, 4, 3, 2, 1] → [4, 5, 3, 2, 1] → [3, 4, 5, 2, 1] → [2, 3, 4, 5, 1] → [1, 2, 3, 4, 5]
모든 단계에서 앞에 있는 자료들을 전부 한 칸씩 뒤로 이동해야 한다.
■ 따라서 외부 루프 i=1,...,n−1 반복 동안 while 문에서 i번의 비교가 발생한다. 즉, 비교 연산은 n−1∑i=1i=1+2+3+…+(n−1)=n(n−1)2이므로 O(n2)이고,
■ 이동 연산은 역순으로 정렬된 [5, 4, 3, 2, 1]을 정렬할 때, 리스트의 길이 5가 n이라면 (n=5)
- [4, 5, 3, 2, 1] → 4는 5를 밀어내고 (이동 1번)
- [3, 4, 5, 2, 1] → 3은 4, 5를 밀어내고 (이동 2번)
- [2, 3, 4, 5, 1] → 2는 3, 4, 5를 밀어내고 (이동 3번)
- [1, 2, 3, 4, 5] → 1은 2, 3, 4, 5를 밀어내야 정렬이 완료된다. (이동 4번 ⇔n−1번 이동)
즉 \( 1 + 2 + \ldots + (n - 1) = \dfrac {n(n-1)}{2} \)이므로 시간 복잡도는 O(n2)이 된다.
■ 삽입 정렬의 시간 복잡도는 O(n2)이므로 레코드의 크기가 커지고, 레코드의 양이 많아질수록 비효율적이지만, 대부분의 레코드가 정렬되어 있다면 효율적으로 사용될 수 있다.
■ 또한, 삽입 정렬은 안정성을 충족하는 안정된 정렬 방법이다.
■ 예를 들어 [3,2,2∗,1]에 삽입 정렬을 적용하면 (2∗=2)
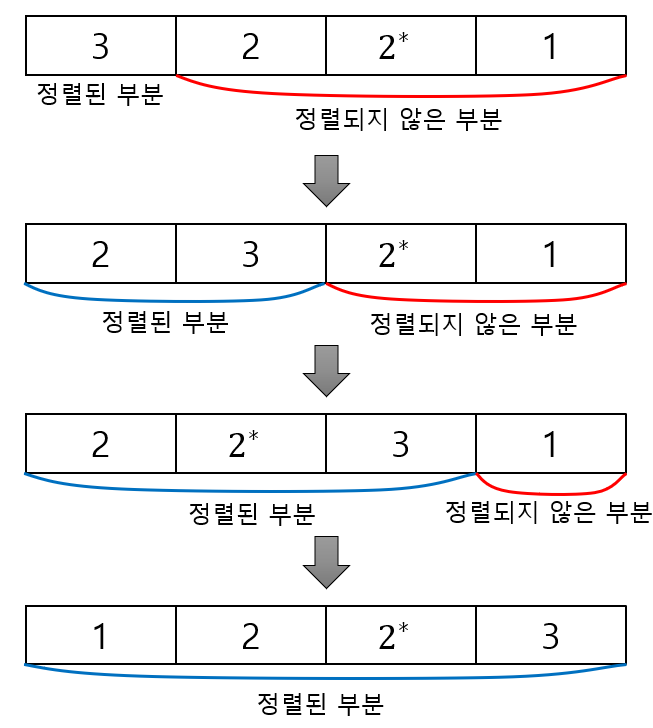
- 이렇게 정렬 후에도 2와 2∗(=2)가 순서대로 위치, 즉 상대적인 위치가 바뀌지 않는 것을 볼 수 있다.
3.3 버블 정렬(Bubble Sort)
■ 버블 정렬은 인접한 2개의 원소를 비교하여 크기 순서에 맞게 서로 교환하는데, 이 비교 - 교환 과정을 리스트 왼쪽부터 오른쪽 끝까지, 리스트 전체에 스캔을 수행한다.
■ 한 번의 스캔이 끝나면 리스트의 오른쪽 끝에는 가장 큰 원소가 위치하게 되고, 끝으로 이동한 원소를 제외하고 더 이상 교환이 일어나지 않을 때까지 스캔을 반복한다.
■ 예를 들어 [5, 3, 8, 4, 9, 1]은 첫 번째 스캔에서
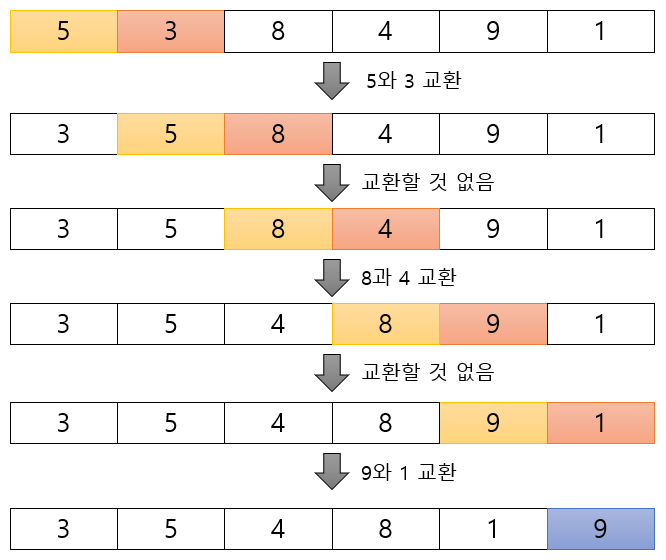
이렇게 한 번 스캔이 완료되면 리스트의 오른쪽 끝에 가장 큰 원소가 위치하게 된다.
두 번째 스캔에서는 끝으로 이동한 원소 '9'를 제외하고 스캔이 진행되어 다음과 같이 오른쪽 끝에 크기 순으로 정렬이 되며

더 이상 교환이 발생하지 않을 때까지 스캔을 반복하면 [1, 3, 4, 5, 8, 9]로 리스트가 정렬된다.
3.3.1 버블 정렬 구현
def BubbleSort(lst):
# print(f'초기 상태 {lst}\n')
n = len(lst)
for i in range(n-1, 0, -1): # 마지막 항목부터
swapped = False
for j in range(i):
if lst[j] > lst[j+1]: # 리스트 길이가 n이면 n-1 번 비교
lst[j], lst[j+1] = lst[j+1],lst[j] # 어떤 값(왼쪽 값)이 오른쪽보다 크면 크기 순서에 맞게 swap
swapped = True
if not swapped: # 더 이상 교환할 것이 없으면
break # 종료
# print(f'{n-i} 번째 {lst}\n')lst = [5, 3, 8, 4, 9, 1]
BubbleSort(lst)
```#결과#```
초기 상태 [5, 3, 8, 4, 9, 1]
1 번째 [3, 5, 4, 8, 1, 9]
2 번째 [3, 4, 5, 1, 8, 9]
3 번째 [3, 4, 1, 5, 8, 9]
4 번째 [3, 1, 4, 5, 8, 9]
5 번째 [1, 3, 4, 5, 8, 9]
`````````````■ 버블 정렬도 최선의 경우는 한 번의 스캔 만에 정렬이 종료되는, 리스트가 이미 정렬되어 있는 상태이다. 이때의 비교는 n−1번 발생하므로 시간 복잡도는 O(n)이지만,
■ 최악의 경우인 역순으로 정렬된 경우 n−1∑i=1i=n(n−1)2번의 비교가 발생하여 시간 복잡도는 O(n2)이다.
■ 또한 최악의 경우, 'lst[j], lst[j+1] = lst[j+1],lst[j]'에서 대입 연산이 발생하여 이동 연산은 3×n(n−1)2으로 비교 연산보다 더 많은 시간이 소요되므로 효율적이지는 않지만, 삽입 정렬처럼 안정성이 충족된다.
lst = [3, 2, 2, 1]
BubbleSort(lst)
```#결과#```
초기 상태 [3, 2, 2, 1]
1 번째 [2, 2, 1, 3]
2 번째 [2, 1, 2, 3]
3 번째 [1, 2, 2, 3]
````````````■ 이렇게 기본 정렬인 선택, 삽입, 버블 정렬은 모두 최악의 경우 시간 복잡도 O(n2)이 된다.
4. 고급 정렬 알고리즘
■ 기본 정렬인 선택 정렬은 입력의 크기에 따라 자료 이동 횟수가 결정되며, 삽입 정렬과 버블 정렬은 안정성을 충족하지만 자료의 많은 이동이 필요하고, 대부분의 자료가 이미 정렬되어 있는 경우에만 효율적이었다.
■ 이러한 기본 정렬은 최악의 경우 시간 복잡도가 O(n2)이므로, 정렬해야 할 자료가 많고, 자주 정렬해야 한다면 더 효율적인 방법이 필요하다.
■ 기본 정렬보다 구현은 복잡하지만, 시간 복잡도는 더 낮아 효율적인 정렬 방법으로 다음과 같은 방법들이 있다.
- 셸 정렬: 삽입 정렬 개념을 개선한 방법
- 힙 정렬: 제자리 정렬로 구현하는 방법
- 병합 정렬: 연속적인 분할과 병합을 이용
- 퀵 정렬, 이중 피벗 퀵 정렬: 피벗을 이용한 정렬
- 기수, 카운팅 정렬: 분배를 이용한 정렬, 키 값에 제한이 있음
4.1 셸 정렬(Shell Sort)
■ 셸 정렬은 삽입 정렬이 대부분의 자료가 이미 정렬되어 있는 경우 효율적인 것에 착안한 방법으로,
- 1) 배열 전체를 한꺼번에 정렬하지 않고,
- 2) 먼저 리스트를 일정한 기준에 따라 여러 개의 부분 리스트로 나누어,
- 3) 각 부분 리스트를 삽입 정렬을 이용해 정렬한다.
- 4) 모든 부분 리스트가 정렬되면 다시 전체 리스트를 더 작은 개수의 부분 리스트로 만들어 앞의 과정을 부분 리스트의 개수가 1이 될 때까지 반복한다.
■ 이런 방법은 자료들의 일부를 정렬시켜 놓고 마지막에 배열 전체를 삽입 정렬해야 할 때, 삽입 정렬 처리 시간을 줄이기 위해서이다.
■ 각 부분 리스트는 전체 리스트에서 거리가 k 만큼 떨어진 요소들로 구성된다. 이때의 k를 간격(gap)이라 하며, k 값은 부분 리스트의 개수와 같다.
- 보통, 전체 리스트의 길이의 절반을 k의 초깃값으로 사용하며, 단계별로 k를 절반씩 줄이는 방식을 사용한다.
■ 예를 들어 [5, 3, 8, 4, 9, 1, 6, 7, 2]일 때, 초기 k는 배열 크기의 절반인 5를 사용하면 (k = 5), 다음과 같이 거리가 5 만큼 떨어진 요소들로 구성된 부분 리스트 5개로 나뉜다.
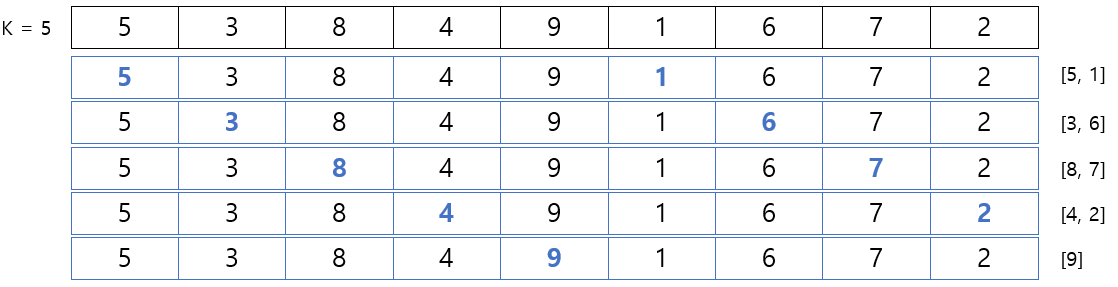
- 각 부분 리스트 [5, 1], [3, 6], [8, 7], [4, 2], [9]를 삽입 정렬을 이용해 정렬하면 [1, 5], [3, 6], [7, 8], [2, 4], [9]이므로 [1, 3, 7, 2, 9, 5, 6, 8, 4]로 변경된다.
- 그 다음, k를 절반 줄여 k = 3일 때

- 각 부분 리스트 [1, 2, 6], [3, 9, 8], [7, 5, 4]를 삽입 정렬을 이용해 정렬하면 [1, 2, 6], [3, 8, 9], [4, 5, 7]이므로 [1, 3, 4, 2, 8, 5, 6, 9, 7]으로 변경된다.
- 마지막으로 k = 1로 줄였을 때, k = 1은 결국, 전체 리스트를 삽입 정렬하는 것을 의미한다. 따라서 최종적으로 [1, 3, 4, 2, 8, 5, 6, 9, 7]을 삽입 정렬하면 다음과 같다.

4.1.1 셸 정렬 구현
■ 셸 정렬을 구현하기 위해선 각 부분 리스트에 대해 k 만큼 떨어진 요소들을 삽입 정렬하는 함수가 필요하다.
def KGapInsertionSort(lst, first, last, k):
for i in range(first+k, last+1, k):
key = lst[i] # k = 5이면 key = lst[5]
j = i - k # 인덱스 i와 5 만큼 떨어진 인덱스 j
while j >= first and key < lst[j]: # key 값 < k 만큼 떨어진 항목의 값
lst[j+k] = lst[j] # swap
j = j-k
lst[j+k] = key # swap
def ShellSort(lst):
n = len(lst)
k = n//2 # k 초깃값을 리스트 크기의 절반으로
while k > 0:
if k % 2 == 0:
k += 1 # k가 짝수이면 1을 더함
for i in range(k):
KGapInsertionSort(lst, i, n-1, k) # k 만큼 떨어진 요소들을 삽입 정렬
print(f'k = {k}, {lst}')
k = k//2 # k = 1이 될 때까지 k를 절반으로lst = [5, 3, 8, 4, 9, 1, 6, 7, 2]
ShellSort(lst)
```#결과#```
k = 5, [1, 3, 7, 2, 9, 5, 6, 8, 4]
k = 3, [1, 3, 4, 2, 8, 5, 6, 9, 7]
k = 1, [1, 2, 3, 4, 5, 6, 7, 8, 9]
````````````■ 삽입 정렬과 비교했을 때, 삽입 정렬은 항상 간격이 k = 1이지만, 셸 정렬은 리스트의 길이가 길어지더라도 k를 설정해 자료의 위치 교환이 발생하므로, k = 1에 가까워질수록 대부분의 항목들이 정렬되어 최종 삽입 정렬(k = 1)에서 삽입 정렬보다 처리 시간이 빨라질 수 있다.
■ 셸 정렬의 시간 복잡도는 최악의 경우 O(n2)이지만, 최선의 경우 O(nlogn)으로 알려져 있다.
4.2 힙 정렬(Heap Sort)
■ 힙은 우선순위 큐를 완전이진트리로 구현하는 방법이다. 최대 힙인지 최소 힙인지에 따라 최댓값이나 최솟값을 루트 노드에 저장하기 때문에 해당 값들을 쉽게 꺼낼 수 있는 자료구조이다.
■ 최대 힙을 사용할 경우, 최대 힙은 가장 큰 항목부터 출력하므로 오름차순 정렬을 하기 위해선 입력 자료들이 저장된 리스트의 맨 뒤부터 출력해야 한다.
■ 이러면 시간 복잡도는 힙의 삽입과 삭제 연산을 거쳐야 하고 삽입, 삭제 시 모든 원소(n)개에 이런 연산을 적용해야 하므로 힙의 삽입, 삭제 시간 복잡도 O(log2n)에 2n번이 곱해져 시간 복잡도는 O(nlogn)이 된다.
■ 기본 정렬 알고리즘에 비해 효율적인 시간 복잡도를 갖지만, 입력 자료의 모든 항목을 다른 메모리 공간인 힙에 모두 넣었다 빼야하기 때문에 추가적인 메모리를 필요로 한다.
■ 이는 제자리 정렬(in - place sorting)로 힙 정렬을 구현하면 추가적인 메모리를 사용하지 않고 구현할 수 있다.
- 이 방법은 먼저
- 1) 입력 배열, 리스트를 최대 힙으로 만들고
- 2) 최대 힙을 정렬된 리스트(오름차순으로 정렬된 리스트)를 만든다.
■ 정렬되지 않은 배열을 최대 힙으로 만드는 과정은 배열의 맨 뒤의 항목부터 시작해 앞으로 가면서 힙 성질을 만족시키면 된다. 이때, 리프 노드는 트리에서 가족 관계가 아니므로 이미 힙을 이루고 있다고 볼 수 있다.
■ 예를 들어 정렬되지 않은 배열 [5, 3, 8, 4, 9, 1, 6, 2, 7]을 트리로 나타냈을 때, 다음과 같다면

- 맨 뒤의 항목 7부터 2, 6, 1, 9 리프 노드는 트리에서 가족 관계가 아니므로 이미 힙을 이루고 있다고 볼 수 있다.
- 따라서 노드 '4'부터 맨 앞 항목 '5'까지 순서대로 다운 힙을 진행하면 최대 힙이 만들어진다.
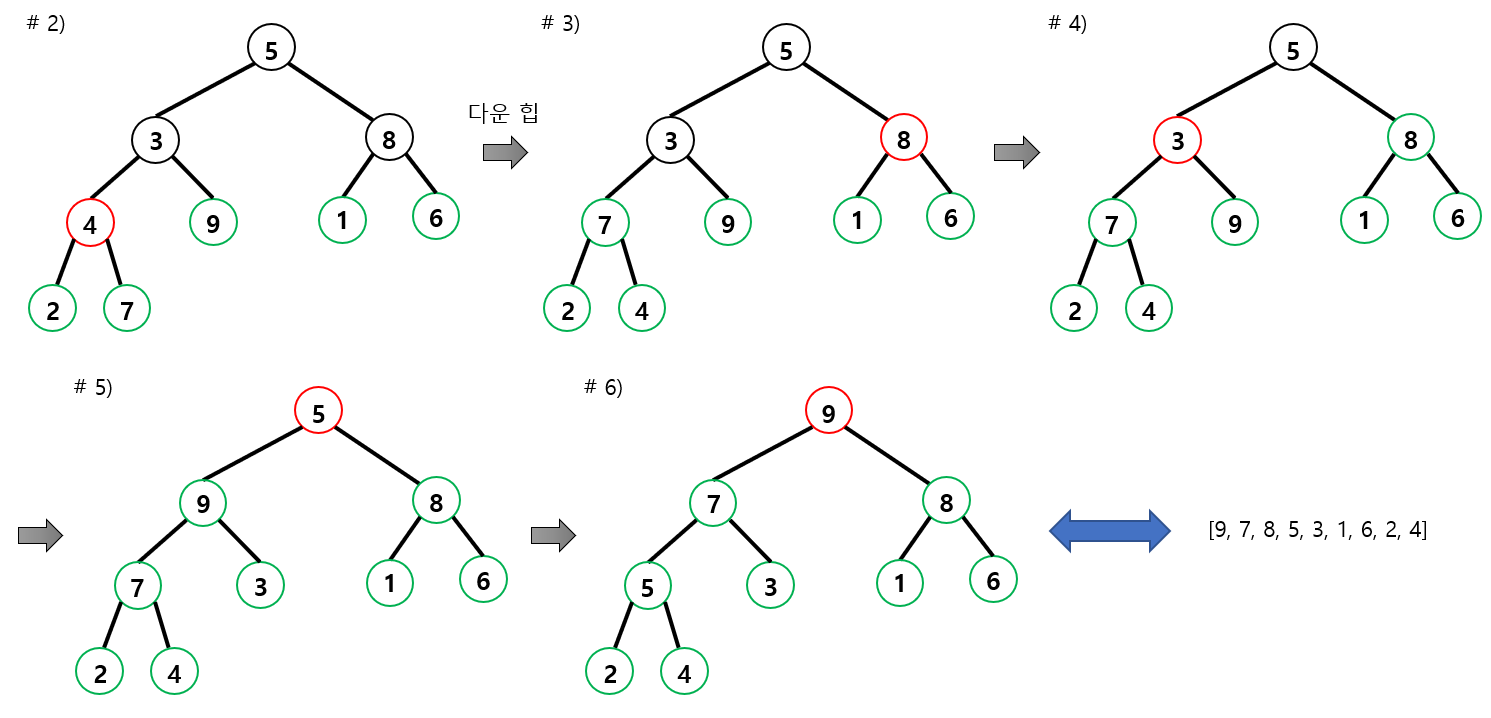
4.2.1 힙 정렬 구현
■ 위와 같은 다운 힙은 배열과 배열 길이, 그리고 다운 힙을 진행할 인덱스를 받아서
■ 배열의 길이를 이용해 왼쪽 자식 노드가 존재하고 i보다 i의 왼쪽 자식이 더 크면 largest는 왼쪽 자식 노드로 갱신하고, 오른쪽 자식 노드가 존재하고 largest보다 오른쪽 자식이 더 크면 largest를 오른쪽 자식 노드로 갱신한다. 즉, largest는 더 큰 자식 노드의 인덱스 정보를 저장하는 역할을 한다.
■ 예를 들어 [10, 15, 20, 17, 15]가 있다고 할 때, 인덱스를 0부터 사용하면,

- i=1일 때, i의 left = 3 < n = 5가 성립하여 i=1의 왼쪽 자식 노드가 존재함을 알려주고, i의 right = 4 < n = 5가 성립하여 i=1의 오른쪽 자식 노드가 존재함을 알려준다.
- i=2일 때, left = 5 < n = 5가 성립하지 않는데, 이는 i=2의 왼쪽 자식이 없음을 알려준다. right = 6 < n = 5이므로 i=2의 오른쪽 자식도 없음을 알려준다.
- 이러한 이유는 인덱스 i의 왼쪽, 오른쪽 자식 인덱스의 값이 배열의 길이보다 크므로, 해당 인덱스들이 리스트 내에 없다는 것을 의미하며, 이 리스트 항목들의 인덱스가 그대로 트리에 적용되므로, '리스트에 해당 인덱스가 없다 == 트리에 해당 인덱스와 부합되는 노드가 없다'가 성립되기 때문이다.
■ largest가 갱신되어 더 이상 largest == i가 아닐 때, 다운 힙을 진행해야 한다. 따라서 i와 largest 인덱스를 가지는 노드들을 서로 교환한다.
■ 교환 후, 더 큰 자식 노드에서 힙의 성질을 유지하는지 위의 과정으로 확인해야 한다.
def heapify(lst, n, i):
left = 2*i + 1 # 왼쪽 자식
right = 2*i + 2 # 오른쪽 자식
largest = i # 다운 힙을 진행할 i 번째 노드가 가장 크다고 가정,
# largest는 더 큰 자식 노드가 있다면 그 자식 노드의 인덱스 정보를 저장하는 역할
if left < n and lst[i] < lst[left]: # 왼쪽 자식이 존재하고 현재 노드보다 왼쪽 자식이 더 크면
largest = left # largest = left로 갱신
if right < n and lst[largest] < lst[right]: # 오른쪽 자식이 존재하고 현재 노드보다 오른쪽 자식이 더 크면
largest = right # largest = right로 갱신
if largest != i:
lst[i], lst[largest] = lst[largest], lst[i] # swap
heapify(lst, n, largest) # 힙 성질을 유지하는지 순환 호출을 통해 더 큰 자식에게 다시 이 과정을 반복■ 마지막으로 단계 2) 최대 힙에서 항목들을 하나씩 꺼내 순서대로 저장하여 정렬된 리스트를 만들어야 한다. 최대 힙으로 리스트를 오름차순 정렬시키려면, 힙의 마지막 인덱스에 위치한 항목부터 순서대로 꺼내야 한다.
■ 이때, 항목을 하나씩 꺼내면(삭제하면) 힙 성질을 만족하지 않을 수 있으므로, 항목을 꺼낸 후 위에서 구현한 heapify( ) 함수를 다시 이용해 힙 성질을 유지시켜야 한다.
def build_heap(lst, n): # 주어진 배열을 최대 힙으로 변환
# print('Max Heap\n')
for i in range(n//2, -1, -1): # 리스트의 중간 인덱스부터 역순으로 heapify 적용
heapify(lst, n, i)
print(f'{i}: {lst}\n')
# print('---'*10)
# print('Heap Sort\n')
def HeapSort(lst):
n = len(lst)
build_heap(lst, n)
for i in range(n-1, 0, -1): # 최대 힙이니까 역순으로 마지막 노드부터 루트 노드까지
lst[i], lst[0] = lst[0], lst[i] # swap
heapify(lst, i, 0) # 역순으로 꺼내므로 전체 노드의 수 i가 하나씩 감소할 때마다
#루트 노드(0번 인덱스)를 갖는 서브트리에 대해 heapify를 호출하여 힙의 성질을 유지하게 한다.
# print(f'{i}: {lst}\n')lst = [5, 3, 8, 4, 9, 1, 6 ,2 ,7]
```#결과#```
Max Heap
4: [5, 3, 8, 4, 9, 1, 6, 2, 7]
3: [5, 3, 8, 7, 9, 1, 6, 2, 4]
2: [5, 3, 8, 7, 9, 1, 6, 2, 4]
1: [5, 9, 8, 7, 3, 1, 6, 2, 4]
0: [9, 7, 8, 5, 3, 1, 6, 2, 4]
------------------------------
Heap Sort
8: [8, 7, 6, 5, 3, 1, 4, 2, 9]
7: [7, 5, 6, 2, 3, 1, 4, 8, 9]
6: [6, 5, 4, 2, 3, 1, 7, 8, 9]
5: [5, 3, 4, 2, 1, 6, 7, 8, 9]
4: [4, 3, 1, 2, 5, 6, 7, 8, 9]
3: [3, 2, 1, 4, 5, 6, 7, 8, 9]
2: [2, 1, 3, 4, 5, 6, 7, 8, 9]
1: [1, 2, 3, 4, 5, 6, 7, 8, 9]
```````````````- 결과를 보면 최대 힙 [9, 7, 8, 5, 3, 1, 6, 2, 4]가 완성된 다음, Heap Sort에서 최대 힙에서 맨 앞의 항목(최댓값 항목)을 계속 꺼내 정렬하는 과정을 볼 수 있다.

■ 제자리 정렬로 구현한 힙 정렬의 시간 복잡도도 O(nlog2n) ≒ O(nlogn) 이다. 단, 최악의 경우에도 시간 복잡도가 O(nlog2n)이고 제자리 정렬로 구현할 수 있으면, 추가적인 메모리가 필요 없다는 점이 있다.
■ 힙 정렬은 전체에서 일부만 정렬할 경우 유용하다. 예를 들어 n개에서 제일 작은 또는 제일 큰 k개의 레코드만 필요한 경우, 다른 방법들은 n개를 모두 정렬해야 하지만, 힙 정렬은 최소 힙 또는 최대 힙에서 k번만 작은 레코드를 추출할 수 있기 때문이다.
- 예를 들어 위의 예에서 가장 큰 값 3개만 필요한 경우, 최대 힙에서 맨 앞의 항목을 3번만 꺼내 정렬하면 [6, 5, 4, 2, 3, 1, 7, 8, 9]가 된다. 여기서 가장 큰 값 3개인 7, 8, 9를 단순히 추출하면 된다.
4.3 병합 정렬(Merge Sort)
■ 병합 정렬은 분할 정복(Divide and Conquer) 기법에 기반을 두고 있다.
■ 분할 정복은 하나의 문제를 보다 작은 문제들로 분리하고 분할한 문제를 각각 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 방법이다.
■ 만약, 분할된 문제가 충분히 작지 않아 원래의 문제를 해결하기 어렵다면, 문제가 해결될 때까지 분할 정복을 연속으로 다시 적용한다.
■ 병합 정렬은 이 분할 정복 기법에 기반하여, 하나의 리스트를 균등한 크기의 리스트 2개로 분할하고, 분할한 리스트를 각각 정렬시킨 다음, 두 리스트를 다시 합쳐 전체가 정렬된 하나의 리스트로 만드는 방법이다.
■ 만약, 분할한 두 개의 리스트를 병합했을 때 병합된 리스트의 전체 항목이 정렬되지 않았다면, 순환 호출을 통해 병합된 리스트가 정렬될 때까지 분할 정복을 적용하면 된다.
■ 즉, 병합 정렬은 분할 정복 기법을 배열의 정렬에 적용한 방법이다.
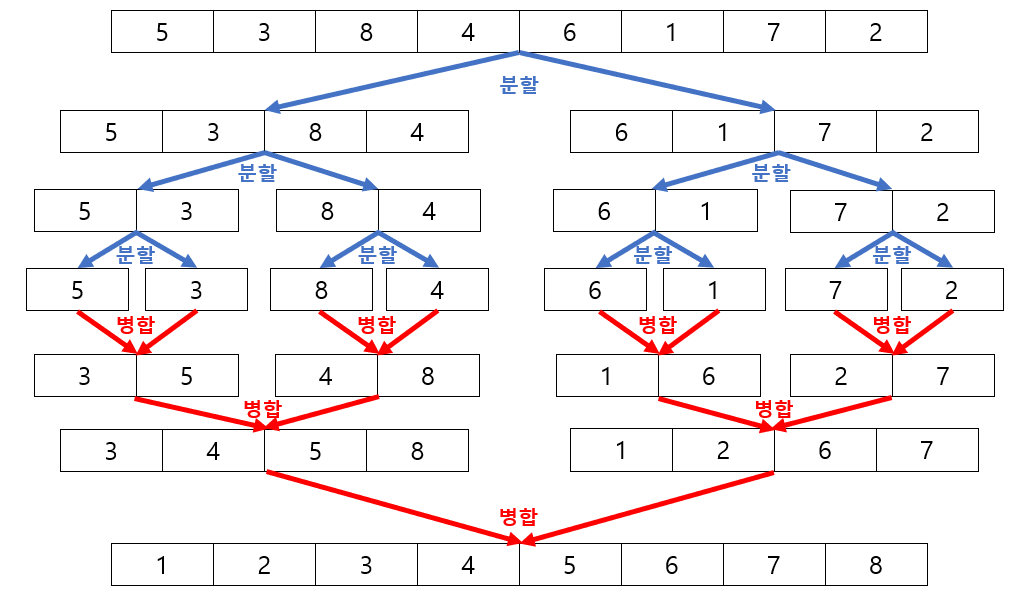
■ 예를 들어 [5, 3, 8, 4, 6, 1, 7, 2]이 있을 때, 병합 정렬은
- 1) 분할(Divide): 전체 배열을 같은 크기의 2개의 배열로 분할한다.
- 2) 정복(Conquer): 부분 배열을 정렬한다. 만약, 배열의 크기가 충분히 작지 않다면 순환 호출을 통해 분할 정복을 재귀적으로 반복한다. 배열의 크기가 1이면 이미 정복된 것이다.
- 이 예에서는 크기가 8인 배열을 분할했을 때, 배열의 크기가 충분히 작지 않아, 순환 호출을 통해 배열의 크기가 1이 될 때까지 다시 분할을 적용한다.
- 3) 병합(Merge): 정렬된 부분 배열들을 하나의 배열로 결합한다.
4.3.1 병합 정렬 구현
■ 위의 방법과 같은 병합 정렬을 구현하기 위해선 분할 정복할 전체 리스트와 이 리스트의 첫 번째 항목의 인덱스, 마지막 원소의 인덱스 정보가 필요하다. 두 인덱스를 활용해 분할 지점을 찾아야 하기 때문이다.
def MergeSort(lst, p, r): # p는 리스트의 첫 번째, r은 마지막 항목의 인덱스
if p < r: # 순환 호출 종료 조건 p >= r
q = (p+r) // 2 # 분할 지점
MergeSort(lst, p, q) # 부분 리스트 1
MergeSort(lst, q+1, r) # 부분 리스트 2
merge(lst, p, q, r) # 병합
return lst■ 다음으로, 실제 정렬이 이루어지는 시점인 2개의 리스트를 병합하는 단계를 구현해야 한다.
■ 병합 방법은 각각의 정렬된 리스트의 맨 왼쪽 항목부터 하나씩 비교하여 두 원소들 중 더 작은 항목을 새로운 리스트에 옮겨 담으면 된다. 새로운 리스트에 모두 옮겨지면 병합은 종료된다.
■ 예를 들어 위의 예에서 각각 정렬된 배열 [3, 4, 5, 8]과 [1, 2, 6, 7]이 병합되는 과정을 보면 다음과 같다.
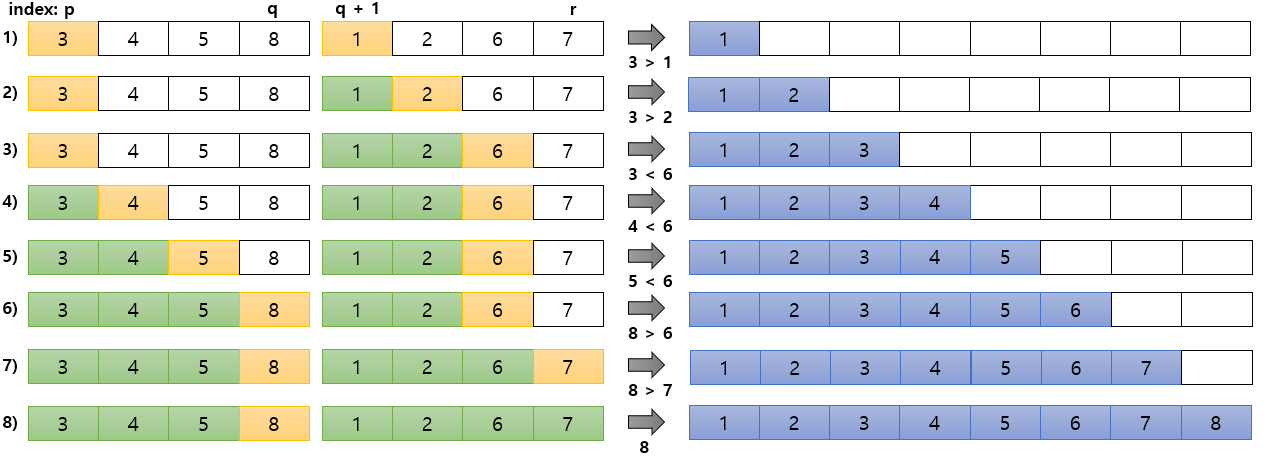
■ 위와 같이 병합을 하기 위해선 분할된 각각의 배열들이 반드시 정렬된 상태여야 한다. 또한, 두 배열의 항목을 비교해서 더 작은 항목을 옮기기 위해 새로운 배열도 필요하다.
■ 병합 단계를 구현하면 다음과 같다. 핵심은 정렬된 두 배열 list[p : q+1], listp[q+1 : r + 1]을 합쳐 정렬된 새로운 배열을 만드는 것이다.
def merge(lst, p, q, r):
tmp = [] # 옮겨 담을 새로운 리스트
i, j = p, q+1
while i <= q and j <= r: # 인덱스 i와 j 중 하나가 각각의 리스트의 마지막 인덱스에 도달할 때까지
if lst[i] <= lst[j]: # 정렬된 두 배열의 항목 비교
tmp.append(lst[i])
i += 1
else:
tmp.append(lst[j])
j += 1
while i <= q: # 왼쪽 배열에 항목이 남아 있는 경우
tmp.append(lst[i]) # i가 끝까지 도달할 때까지 남은 항목들을 tmp에 추가
i += 1
while j <= r: # 오른쪽 배열에 항목이 남아 있는 경우
tmp.append(lst[j]) # j가 끝가지 도달할 때까지 남은 항목들을 tmp에 추가
j += 1
lst[p:r+1] = tmp # 정렬된 배열을 원래 배열 lst에 복사MergeSort([5, 3, 8, 4, 6, 1, 7, 2], 0, 7)
```#결과#```
[1, 2, 3, 4, 5, 6, 7, 8]
````````````■ 병합 정렬을 위와 같이 크기가 n인 리스트로 균등 분배하므로, n→n2→n4→…→1 즉, 리스트를 두 개로 나누는 과정이 log2n만큼 발생한다. 병합 단계도 마찬가지이다.
■ 그리고 하나의 병합 단계에서 n번의 비교 연산이 발생하고 병합하는 과정이 log2n번 필요하므로 비교 연산은 최대 O(nlog2n)번 필요하다.
■ 이동 연산도 항목이 n개인 경우 tmp.append(lst[i]), tmp.append(lst[j])에서 원래 리스트 lst에서 요소를 tmp로 복사하는 이동 연산이므로 총 n번 이동이 발생하고, lst[p:r + 1] = tmp에서도 n개의 요소가 원래 리스트로 이동하기 때문에 총 n번 이동이 발생하여 하나의 병합 단계에서 2n이 발생한다. 따라서 이동 연산은 2n × log2n번의 이동 연산이 필요하다.
■ 결론적으로 병합 정렬은 최선, 평균, 최악 모두 O(nlog2n)의 복잡도를 가지는 정렬 방법이다. 즉, 입력 데이터의 형태에 상관없이 모든 경우에서 동일한 시간에 정렬된다는 것이다. 다만, 새로운 리스트가 필요하므로 추가적인 메모리가 필요하다는 단점이 있다.
4.4 퀵 정렬(Quick Sort)
■ 퀵 정렬은 병합 정렬처럼 분할 정복 기법을 사용하지만, 병합 정렬과 달리 하나의 전체 리스트를 균등하게 분할할 필요 없이 순환 호출을 이용해 각각의 부분 리스트를 다시 퀵 정렬한다.
4.4.1 퀵 정렬 구현
■ 이러한 퀵 정렬 방법은 다음과 같다.
- 1) 먼저 리스트 안에 있는 한 요소를 피벗(pivot)으로 선택한다.
- 2) 그리고 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽에, 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮긴다.
- 3) 퀵 정렬은 이 상태에서 피벗을 기준으로 나누어진 왼쪽 부분 리스트와 오른쪽 부분 리스트에 재귀 호출을 사용하여 각 부분 리스트 내에서 피벗을 정하고 피벗을 기준으로 다시 2개의 부분 리스트로 나누는 과정을 부분 리스트를 더 이상 분할할 수 없을 때까지 반복한다.
def QuickSort(lst, p, r): # p는 리스트의 첫 번째, r은 마지막 항목의 인덱스
if p < r: # 따라서 p = r이면 하나의 항목만 가지는 리스트. 즉, 분할할 리스트가 없음
q = partition(lst, p, r)
QuickSort(lst, p, q-1) # 피벗 왼쪽 부분. 재귀 호출을 통해 퀵 정렬
QuickSort(lst, q+1, r) # 피벗 오른쪽 부분. 재귀 호출을 통해 퀵 정렬
■ 퀵 정렬에서 핵심은 분할을 진행하는 partition 함수이다.
■ partition 함수는 일단 배열의 첫 번째 항목을 피벗으로 설정해서, 피벗을 기준으로 전체 배열을 2개의 부분 리스트로 나누는데, 피벗보다 작은 항목을 모두 왼쪽 부분 리스트, 피벗보다 큰 항목은 모두 오른쪽 부분 리스트로 옮겨야 한다.
■ 예를 들어 다음과 같은 배열을 피벗으로 두 개의 부분 리스트로 나눈다면
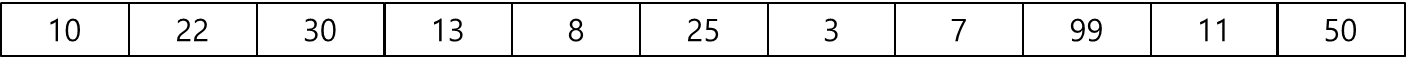
- 1) 피벗 설정

- 2) 위와 같이 배열의 첫 번째 항목(인덱스 p)을 피벗으로 설정하고 인덱스 i(= p+1)에서 r까지의 항목을 순회하면서 lst[j]가 (j는 p+1 부터 r까지) 피벗보다 작거나 같으면 i 번째 항목과 j 번째 항목을 교환해서 피벗보다 작은 값들은 리스트 왼쪽에, 큰 값들은 리스트 오른쪽에 모이게 한다.
- 반복문을 통해 먼저 j = p+1일 때, lst[j] <= pivot인지 검사한다. 22(lst[j]) <= 10(pivot)이므로 거짓이다. 따라서 j = p+2으로 넘어가고 이때 j = p+1이다.
- j = p+2일 때, 30(lst[j]) <= 10(pivot)이므로 p+3으로 넘어간다. 이때 i = p+1
- j = p+3일 때, 13(lst[j]) <= 10(pivot)이므로 p+4으로 넘어간다. 이때 i = p+1
- j = p+4일 때, 8(lst[j]) <= 10(pivot)으로 참이므로 lst[i], lst[j] = lst[j], lst[i]으로 swap을 한다. 그러면 p+1 인덱스에는 pivot보다 작은 8이, p+4 위치에는 기존 p+1 위치에 있던 22가 위치하게 된다. 그리고 현재 i(= p+1)위치에 피벗보다 작은 값을 배치시켰으므로 i를 1 증가시켜 i+1(= p+2) 위치에 올 항목을 탐색한다.
- 다음으로 j = p+5일 때, pivot이 크므로 j = p+6으로 넘어가고 pivot보다 작거나 같으므로 lst[p+2], lst[p+6] = lst[p+6], lst[p+2] 교환이 발생, i = i+2 = p+3이 된다.
- j = p+7일 때도 swap이 발생하고 i = p+4가 된다. 이후에 j = p+8부터 j = r까지 피벗보다 크므로 swap은 발생하지 않고 i = p+4가 유지되며, 현재 배열의 모습은 다음과 같이 왼쪽에는 피벗보다 작거나 같은 값, 피벗보다 작거나 같은 값의 오른쪽부터는 피벗보다 큰 값들이 위치하게 된다.

■ 즉, 피벗보다 작거나 같은 값들의 위치를 모두 옮기게 되면, 위의 배열 그림과 같이 피벗보다 작거나 같은 값과 피벗보다 큰 값이 서로 인접하게 되는 인덱스를 알 수 있다. 이 예에서는 p+4이다.
■ 이 인덱스는 피벗보다 큰 값의 리스트, 즉 오른쪽 리스트가 되었을 때, 오른쪽 리스트의 첫 번째 항목을 가리키게 된다. 이 인덱스를 i∗라 하면,
■ 피벗을 기준으로 두 개의 부분 리스트를 나누기 위해선 i∗ 이전 인덱스인 i∗−1 인덱스의 위치에 피벗이 위치해야 한다.
- 따라서 lst[i-1], lst[p] = lst[p], lst[i-1] swap을 통해 피벗의 위치를 옮겨준다. 이 예에서 현재 i∗=p+4이므로, lst[p+4-1], lst[p] = lst[p], lst[p+4-1]로 swap이 발생하고 배열은 다음과 같이 피벗을 기준으로 왼쪽에는 피벗보다 작거나 같은 값, 오른쪽에는 피벗보다 큰 값이 위치하게 된다.

■ 위와 같이 한 번의 partition으로 배열이 정렬되지 않을 수 있기 때문에 현재 i - 1 인덱스를 반환해서, 왼쪽 리스트(인덱스 p부터 q = i - 1)와 오른쪽 리스트(인덱스 q + 1 = i - 1 + 1부터 r)에 재귀 호출로 퀵 정렬을 적용시켜야 한다.
def partition(lst, p, r):
pivot = lst[p]
i = p+1
for j in range(p+1, r+1):
if lst[j] <= pivot:
lst[i], lst[j] = lst[j], lst[i]
i += 1
# print(f'swap {lst}')
lst[i-1], lst[p] = lst[p], lst[i-1]
# print(lst)
return i-1lst = [10, 22, 30, 13, 8, 25, 3, 7, 99, 11, 50]
QuickSort(lst, 0, len(lst)-1)
```#결과#```
swap [10, 22, 30, 13, 8, 25, 3, 7, 99, 11, 50]
swap [10, 22, 30, 13, 8, 25, 3, 7, 99, 11, 50]
swap [10, 22, 30, 13, 8, 25, 3, 7, 99, 11, 50]
swap [10, 8, 30, 13, 22, 25, 3, 7, 99, 11, 50]
swap [10, 8, 30, 13, 22, 25, 3, 7, 99, 11, 50]
swap [10, 8, 3, 13, 22, 25, 30, 7, 99, 11, 50]
swap [10, 8, 3, 7, 22, 25, 30, 13, 99, 11, 50]
swap [10, 8, 3, 7, 22, 25, 30, 13, 99, 11, 50]
swap [10, 8, 3, 7, 22, 25, 30, 13, 99, 11, 50]
swap [10, 8, 3, 7, 22, 25, 30, 13, 99, 11, 50]
5 [7, 8, 3, 10, 22, 25, 30, 13, 99, 11, 50]
swap [7, 8, 3, 10, 22, 25, 30, 13, 99, 11, 50]
swap [7, 3, 8, 10, 22, 25, 30, 13, 99, 11, 50]
5 [3, 7, 8, 10, 22, 25, 30, 13, 99, 11, 50]
swap [3, 7, 8, 10, 22, 25, 30, 13, 99, 11, 50]
swap [3, 7, 8, 10, 22, 25, 30, 13, 99, 11, 50]
swap [3, 7, 8, 10, 22, 13, 30, 25, 99, 11, 50]
swap [3, 7, 8, 10, 22, 13, 30, 25, 99, 11, 50]
swap [3, 7, 8, 10, 22, 13, 11, 25, 99, 30, 50]
swap [3, 7, 8, 10, 22, 13, 11, 25, 99, 30, 50]
5 [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
5 [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
5 [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
swap [3, 7, 8, 10, 11, 13, 22, 25, 99, 30, 50]
5 [3, 7, 8, 10, 11, 13, 22, 25, 50, 30, 99]
swap [3, 7, 8, 10, 11, 13, 22, 25, 50, 30, 99]
5 [3, 7, 8, 10, 11, 13, 22, 25, 30, 50, 99]■ 피벗 정렬의 최선의 경우는 리스트가 다음 그림과 같이 균등 분할되어 항상 리스트의 가운데에서 분할이 이루어지는 상황이다.
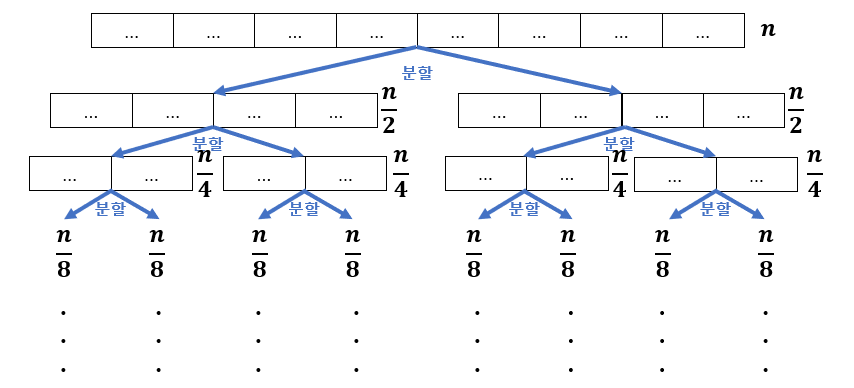
■ 위와 같이 리스트 크기가 n2k로 \( \dfrac {n}{2}, \dfrac {n}{4}, \dfrac {n}{8}, \dots \)으로 나눠지기 시작해 리스트 크기가 1이 될 때까지 분할된다. 즉 n2k=1일 때까지 균등 분할로 나누어질 것이므로 k=log2n번의 분할이 필요하다.
■ 그리고 각각의 패스에서 전체 리스트 대부분의 항목을 비교하므로, 비교 연산의 수는 n번이다.
■ 따라서 최선의 경우 균등 분할이 계속 이루어질 때, 퀵 정렬의 비교 연산은 n\timelog2n번 이므로 비교 연산의 시간 복잡도는 o(nlog2n)이다.
■ 최악의 경우는 리스트가 계속 불균형하게 나누어지는 경우이다.
■ 특히, 이미 정렬된 배열을 퀵 정렬할 경우 시간 복잡도는 비교 연산의 수가 n이고 매우 불균형하게 1과 n−1 크기로 분할될 경우 n번의 분할이 필요하다. 따라서 최악의 경우 비교 연산은 n\timen번 이므로 시간 복잡도는 O(n2)이 된다.
■ 퀵 정렬의 평균적인 시간 복잡도는 o(nlog2n)으로, 다른 고급 정렬 알고리즘과 비교했을 때 속도가 빠른 것으로 알려져 있다. 이것은 먼 거리의 데이터를 교환하여 불필요한 이동을 줄인 점과 한 번 정렬된 피벗은 추후 연산에서 제외되는 특징 때문이다.
■ 불균형 분할의 문제점(이미 정렬된 배열을 퀵 정렬)을 완화하기 위해 피벗을 첫 번째 항목이 아닌 중앙 값(median)을 피벗으로 선택하는 방법이 있다.
■ 예를 들어 정렬된 배열에서 첫 번째 항목이 아닌 중앙 값을 피벗으로 선택한다면, 피벗을 기준으로 피벗 왼쪽에는 피벗보다 작은 값, 피벗 오른쪽에는 큰 값이 위치하게 되어 불균형 분할의 문제점을 완화시킬 수 있다.

4.5 이중피벗 퀵 정렬(Dual Pivot Quick Sort)
■ 이중피벗 퀵 정렬은 퀵 정렬을 보완하여 2개의 피벗을 사용하는 퀵 정렬이다.
- 1) 이중피벗 퀵 정렬은 리스트 양쪽 끝에 있는 피벗을 선택한다. 이 두 개의 피벗을 lp, rp라고 했을 때, 항상 lp의 값이 rp의 값보다 크지 않도록 조정 해준다.
- 2) 그리고 lp와 rp를 기준으로, lp의 왼쪽에는 ① lp보다 작은 값, rp 오른쪽에는 ② rp보다 큰 값, ③ lp와 rp 사이의 값, 이렇게 3개의 그룹으로 나눈다.
- 이렇게 이중피벗 퀵 정렬은 두 개의 피벗을 이용해 하나의 리스트를 세 부분으로 분할한다.
- 3) 마지막으로 퀵 정렬처럼 재귀적 호출을 통해 정렬이 될 때까지 이 과정을 반복한다.
4.5.1 이중피벗 퀵 정렬 구현
■ 이중피벗 퀵 정렬도 퀵 정렬처럼 분할 연산 메서드를 구현해 줘야 하며, 이 부분이 핵심이다.
■ 정렬할 리스트와 이 리스트의 가장 낮은 인덱스(리스트 맨 왼쪽)와 가장 높은 인덱스(리스트 맨 오른쪽)를 받아서 왼쪽 피벗과 오른쪽 피벗의 인덱스로 사용한다.
■ 그리고 왼쪽 피벗과 오른쪽 피벗의 인덱스를 이용해 3개의 인덱스를 정의한다.
- 왼쪽 피벗보다 작은 요소들이 위치해야 하는 경계를 나타내는 인덱스와 오른쪽 피벗보다 큰 요소들이 위치해야 하는 경계를 나타내는 인덱스
- 이 두 인덱스는 왼쪽 피벗 바로 다음의 위치와 오른쪽 피벗 직전의 위치를 이용하면 된다. 이 두 인덱스를 i,j라 하자.
- 현재 요소를 왼쪽 피벗, 오른쪽 피벗과 비교해 적절한 위치로 교환하기 위한 인덱스를 정의한다. 이 인덱스는 왼쪽 피벗 다음 요소부터 오른쪽 피벗 이전의 요소들을 적절한 영역으로 분류해야 하므로 왼쪽 피벗 다음의 위치에서 시작해야 한다. 이 인덱스를 k라 하자.
■ 요소의 위치 교환이나 인덱스 연산은 4가지 경우에서 발생한다.
- ① 왼쪽 피벗이 오른쪽 피벗보다 크다면 두 값의 위치를 교환한다.
- ② k가 가리키는 값이 왼쪽 피벗보다 작으면 k와 i가 가리키는 값을 교환해 왼쪽 피벗보다 작은 값을 왼쪽으로 모이게 한다. 그리고 i와 k를 + 1칸 이동하여 다음 값을 비교해야 한다.
- ③ 반대로, k가 가리키는 값이 오른쪽 피벗보다 크다면 k와 j가 가리키는 값을 교환해 오른쪽 피벗보다 큰 값을 오른쪽에 모이게 해야 한다. 그리고 j도 - 1칸 이동시켜 다음 값을 비교하게 해야 한다.
- ④ k가 가리키는 값이 왼쪽 피벗과 오른쪽 피벗 사이의 값이라면 요소를 교환하지 않고 다음 요소를 비교하기 위해 k를 + 1칸 이동하면 된다.
■ 이렇게 위치 교환이 완료되면, 왼쪽 피벗과 오른쪽 피벗을 올바른 위치에 이동시켜야 한다. 위치 교환이 올바르게 수행되었다면 k > j가 되고 i−1과 j+1의 위치가 왼쪽 피벗, 오른쪽 피벗이 들어갈 경계가 된다.
■ 예를 들어 [7, 6, 8, 4, 9, 3, 2, 5]를 정렬한다면

- ① 왼쪽 피벗이 오른쪽 피벗보다 크므로 교환

- ② k가 가리키는 값이 왼쪽 피벗과 오른쪽 피벗 사이의 값이므로 k만 + 1칸 이동

- ③ k가 가리키는 값이 오른쪽 피벗보다 크므로 list[k]와 list[j]를 교환하고 j를 - 1 만큼 이동

- ④ k가 가리키는 값이 왼쪽 피벗보다 작으므로 list[k]와 list[i]를 교환하고 i,k를 + 1칸 이동
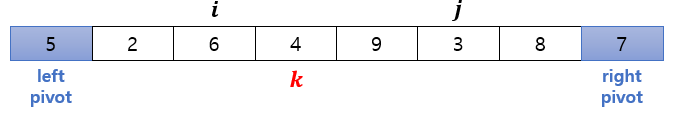
- ⑤ k가 가리키는 값이 왼쪽 피벗보다 작으므로 list[k]와 list[i]를 교환하고 i,k를 + 1칸 이동

- ⑥ k가 가리키는 값이 오른쪽 피벗보다 크므로 list[k]와 list[j]를 교환하고 j를 - 1 만큼 이동

- ⑦ k가 가리키는 값이 왼쪽 피벗보다 작으므로 list[k]와 list[i]를 교환하고 i,k를 + 1칸 이동

- ⑧ 위치 교환이 종료되고 i−1,j+1의 자리가 왼쪽, 오른쪽 피벗이 들어갈 자리가 된다.

def DualPivotQuickSort(lst, low, high):
if low < high:
lp, rp = partition(lst, low, high)
DualPivotQuickSort(lst, low, lp-1)
DualPivotQuickSort(lst, lp+1, rp-1)
DualPivotQuickSort(lst, rp+1, high)def partition(lst, low, high):
# 왼쪽 피벗과 오른쪽 피벗을 정렬
if lst[low] > lst[high]:
lst[low], lst[high] = lst[high], lst[low]
left_pivot = lst[low]
right_pivot = lst[high]
# 포인터 초기화
i = low + 1 # 왼쪽 영역의 경계
j = high - 1 # 오른쪽 영역의 경계
k = low + 1 # 현재 요소를 가리키는 포인터
while k <= j: # 종료 조건 k > j
if lst[k] < left_pivot: # k가 가리키는 값이 왼쪽 피벗보다 작은 경우
lst[k], lst[i] = lst[i], lst[k]
i += 1
k += 1
elif lst[k] > right_pivot: # k가 가리키는 값이 오른쪽 피벗보다 큰 경우
lst[k], lst[j] = lst[j], lst[k]
j -= 1
else: # k가 가리키는 값이 왼쪽 피벗과 오른쪽 피벗의 중간 영역에 속하는 경우
k += 1
# 위치 교환이 끝나면 왼쪽 피벗과 오른쪽 피벗을 올바른 위치에
lst[low], lst[i - 1] = lst[i - 1], lst[low]
lst[high], lst[j + 1] = lst[j + 1], lst[high]
return i - 1, j + 1lst = [7, 6, 8, 4, 9, 3, 2, 5]
DualPivotQuickSort(lst, 0, len(lst)-1)
lst
```#결과#```
[2, 3, 4, 5, 6, 7, 8, 9]
````````````
4.6 기수 정렬(Radix Sort)
■ 기수 정렬은 다른 정렬 방법들과 다르게 어떠한 비교 연산도 수행하지 않고 데이터를 정렬할 수 있으며 시간 복잡도는 O(k⋅n)이다.
■ 단, 기수 정렬은 추가적인 메모리가 필요한데, 이 단점을 감안해도 다른 방법들에 비해 속도가 빠르다.
■ 여기서 기수는 숫자의 자릿수를 의미한다.
■ 예를 들어 5는 일의 자리 한 개의 자릿수, 15는 십의 자리 & 일의 자리로 두 개의 자릿수를 가진다.
■ 기수 정렬은 이 자릿수의 값에 따라 정렬하며, 정렬 단계의 수는 전체 자릿수와 일치한다.
■ 예를 들어 한자리 숫자 [7, 6, 8, 4, 9, 3, 2, 5]에 기수 정렬을 적용하면, 십진수는 각 자릿수가 0에서 9까치 총 10개이므로, 이 10개의 버킷(bucket)을 만들어 데이터 값에 따라 버킷에 넣는다.
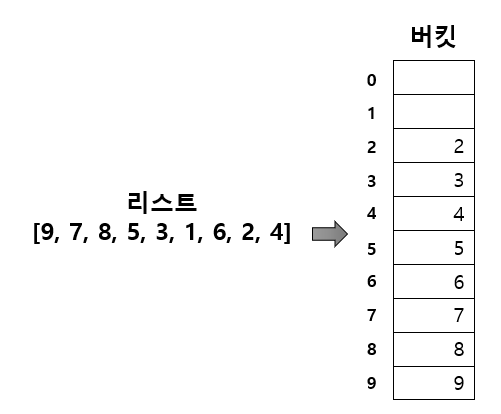
그리고 위쪽부터 순서대로 버킷에 들어 있는 값을 출력하면 비교 연산을 사용하지 않아도 리스트를 정렬할 수 있다.
■ 만약, 자릿수가 2개 이상인 경우
- 예를 들어 [17, 26, 38, 34, 29, 13, 52, 65]는 0에서 99까지 100개의 버킷을 사용해 위의 한자리 정렬처럼 할 수 있지만, 1의 자릿수와 10의 자릿수를 따로 사용해 정렬한다면 10개의 버킷으로 2개의 숫자를 정렬할 수 있다.
- 정렬 순서는 낮은 자릿수 정렬 → 높은 자릿수 정렬이다. 10의 자릿수부터 정렬하면 [17, 13, 26, 29, 38, 34, ... ] 처럼 올바르게 정렬되지 않을 수 있기 때문이다.
- 1의 자릿수 정렬 → 10의 자릿수 정렬을 하면
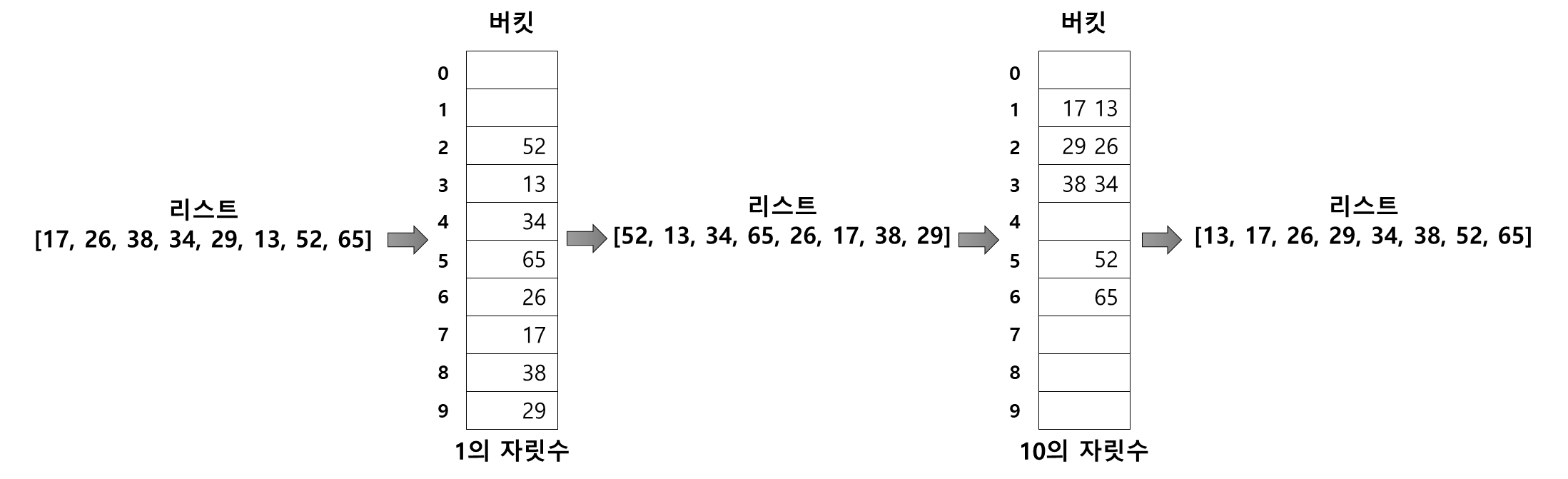
■ 이렇게 십진법을 사용할 경우 10개의 버킷을 사용하면 되지만, 알파벳이라면 A부터 Z가지 26개의 버킷이 필요하다.
4.6.1 기수 정렬 구현
■ 버킷은 먼저 들어간 숫자가 먼저 나와야 순서가 유지되기 때문에, 큐를 이용해 구현한다.
■ 큐를 이용하면 버킷에 넣는 연산은 큐의 enqueue, 버킷에서 빼는 연산은 큐의 dequeue 연산을 사용하면 된다.
def RadixSort(lst):
buckets = [CircularQueue() for _ in range(10)] # 원형 큐를 이용해 버킷 생성
max_num = max(lst)
exp = 1 # 1의 자리부터 정렬 시작
while max_num // exp > 0: # 리스트의 최댓값을 이용해 종료 조건 설정
for num in lst:
digits = (num // exp) % 10
buckets[digits].QEnqueue(num)
# buckets[digits].QShow()
# print('--'*10)
index = 0
for b in range(len(buckets)):
while not buckets[b].QIsEmpty(): # b 번째 큐가 공백 상태가 될 때까지
num = buckets[b].QDequeue() # b 번째 큐에서 요소 반환
lst[index] = num # 버킷에서 반환된 순서대로 리스트에 넣기
# buckets[b].QShow()
index += 1
exp *= 10 # 다음 자릿수로
return lstprint(CircularQueue._CAPACITY)
```#결과#```
4
````````````
lst = [17, 26, 38, 34, 29, 13, 52, 65]
RadixSort(lst)
```#결과#```
[17]
[26]
[38]
[34]
[29]
[13]
[52]
[65]
--------------------
[None, None, None, 52]
[None, None, None, 13]
[None, None, None, 34]
[None, None, None, 65]
[None, None, None, 26]
[None, None, None, 17]
[None, None, None, 38]
[None, None, None, 29]
[52]
[13]
[34]
[65]
[26]
[13, 17]
[34, 38]
[26, 29]
--------------------
[17]
[None, None, 13, 17]
[29]
[None, 52, 26, 29]
[38]
[None, 13, 34, 38]
[None, None, 65, 52]
[None, None, 26, 65]
[13, 17, 26, 29, 34, 38, 52, 65]
``````````````■ 이 예에서 max_num = 65이다.
while max_num // exp > 0:
for num in lst:
digits = (num // exp) % 10
buckets[digits].QEnqueue(num)- 첫 번째 반복에서 65 // exp = 1 > 0은 True이므로 lst에서 50을 꺼내 'digits = (50 // 1) % 10 = 0'을 계산해서 1의 자리가 0인 0번 버킷 큐에 50을 삽입한다.
- 두 번째 반복에서는 65 // exp = 10 > 0은 True이므로 버킷에 항목을 위와 같이 삽입하는데, 세 번째 반복부터 65 // exp = 100은 0이므로 False가 되어 종료된다.
- 즉, max_num과 //, exp를 이용해 정렬할 자릿수의 최대치를 알 수 있다.
■ 위와 같이 구현할 경우, 리스트가 n개의 정수를 가지며 각 정수가 d개의 자릿수를 가진다면, 기수 정렬은 O(d⋅n)의 시간 복잡도를 가지게 된다.
■ 즉, 기수 정렬의 시간 복잡도는 d에 비례하므로 기수 정렬의 수행 시간은 정수의 자릿수에 의존한다. 보통 d가 n에 비해 아주 작은 수가 되므로 O(n)으로 봐도 무방하다.
■ 단점은 원형 큐가 고정된 용량을 가져, 초기 설정한 용량보다 더 많은 요소를 버킷에 넣을 경우 원형 큐의 용량이 초과된다.
lst2 = [50, 41, 17, 26, 38, 34, 29, 13, 52, 65, 100]
RadixSort(lst2)
```#결과#```
---------------------------------------------------------------------------
Exception Traceback (most recent call last)
Cell In[23], line 1
----> 1 RadixSort(lst2)
Cell In[15], line 9, in RadixSort(lst)
7 for num in lst:
8 digits = (num // exp) % 10
----> 9 buckets[digits].QEnqueue(num)
10 buckets[digits].QShow()
12 print('--'*10)
Cell In[8], line 21, in CircularQueue.QEnqueue(self, new_item)
19 def QEnqueue(self, new_item):
20 if self.QIsFull():
---> 21 raise Exception('Queue is full')
22 else:
23 self.rear = (self.rear + 1) % CircularQueue._CAPACITY
Exception: Queue is full
`````````````■ 그러나, 이 문제점은 파이썬의 내장 queue.Queue를 사용할 경우 queue.Queue는 별도의 용량 제한을 설정하지 않는다면 무제한의 용량을 가지므로 위와 같이 큐가 가득 차는 상황이 발생하지 않을 것이다.
■ 단, 다른 정렬 방법과 달리 한글, 한자, 실수 등으로 이루어진 리스트에 기수 정렬을 수행할 경우 매우 많은 버킷이 필요하게 되어, 그만큼의 메모리 사용량이 증가하고 이는 성능 저하로 이어질 수 있다.
■ 따라서 기수 정렬은 정수같은 순서가 있는 특정 유형의 데이터에 한정해 효율적인 알고리즘이다.
4.7 카운팅 정렬(Counting Sort)
■ 카운팅 정렬도 정렬할 값들이 일정 범위를 가진 정수일 때, 기수 정렬처럼 비교 연산을 사용하지 않고 정렬하는 방법이다.
■ 카운팅 정렬은 모든 항목의 빈도수를 저장하기 위한 배열을 만들고, 배열의 인덱스에 해당하는 항목의 값이 나타난 횟수를 카운팅 한다.
■ 예를 들어 [0, 1, 0, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7]이라면, 다음과 같이 인덱스가 0부터 7까지인 배열을 만들어, 배열의 인덱스에 항목의 빈도수를 카운팅한다.

■ 그리고 정렬된 리스트에서 각 항목의 앞에 위치할 항목의 개수를 정하기 위해 다음과 같이 앞의 항목 개수부터 더한다.

즉, 항목 '0'은 1~2 번째, '1'은 3~4 번째, '2'는 5 번째, ... 위치에 정렬함을 의미한다.
■ 마지막으로 리스트 역순으로 순회하면서 올바른 위치에 항목을 배치하면 된다.
4.7 카운팅 정렬 구현
def CountingSort(lst):
max_val = max(lst)
count = [0] * (max_val + 1) # 인덱스 0부터 인덱스 max_val까지 포함해야 하므로
for num in lst:
count[num] += 1 # 항목 count
# print('카운트',count)
for i in range(1, len(count)):
count[i] += count[i-1] # 누적 카운트 배열 계산
# print('누적 카운트:', count)
output = [0] * len(lst) # 결과 배열
i = len(lst) - 1
while i >= 0: # 역순 순회
output[count[lst[i]] - 1] = lst[i]
count[lst[i]] -= 1
i -= 1
for i in range(len(lst)):
lst[i] = output[i]
return lstlst = [0,1,0,1,2,3,3,4,4,4,5,6,7,7]
len(lst)
```#결과#```
14
````````````
CountingSort(lst)
```#결과#```
카운트 [2, 2, 1, 2, 3, 1, 1, 2]
누적 카운트: [2, 4, 5, 7, 10, 11, 12, 14]
[0, 0, 1, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7]
````````````| i | lst[i] | count[lst[i]] | output 인덱스 | output 상태 | count[lst[i]] 업데이트 |
| 13 | 7 | 14 | 13 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7] | 13 |
| 12 | 7 | 13 | 12 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7, 7] | 12 |
| 11 | 6 | 12 | 11 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 6, 7, 7] | 11 |
| 10 | 5 | 11 | 10 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 6, 7, 7] | 10 |
| 9 | 4 | 10 | 9 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 5, 6, 7, 7] | 9 |
| 8 | 4 | 9 | 8 | [0, 0, 0, 0, 0, 0, 0, 0, 4, 4, 5, 6, 7, 7] | 8 |
| 7 | 4 | 8 | 7 | [0, 0, 0, 0, 0, 0, 0, 4, 4, 4, 5, 6, 7, 7] | 7 |
| 6 | 3 | 7 | 6 | [0, 0, 0, 0, 0, 0, 3, 4, 4, 4, 5, 6, 7, 7] | 6 |
| 5 | 3 | 6 | 5 | [0, 0, 0, 0, 0, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 5 |
| 4 | 2 | 5 | 4 | [0, 0, 0, 0, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 4 |
| 3 | 1 | 4 | 3 | [0, 0, 0, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 3 |
| 2 | 0 | 2 | 1 | [0, 0, 0, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 1 |
| 1 | 1 | 3 | 2 | [0, 1, 1, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 2 |
| 0 | 0 | 1 | 0 | [0, 1, 1, 1, 2, 3, 3, 4, 4, 4, 5, 6, 7, 7] | 0 |
■ 카운팅 정렬은 입력 데이터가 크지 않은 일정한 범위의 값을 가진 양수라면, 입력이 n개의 정수를 갖는 리스트일 때 숫자의 범위가 k까지라면(0부터 k−1) O(k+n)의 시간 복잡도를 갖는다. 이때, k가 작은 수라면 O(n)으로 봐도 무방하다.
■ 다만, 카운팅 배열을 저장하기 위해 O(k)의 추가 메모리 공간이 필요하다. 카운팅 배열의 길이는 숫자의 범위 k에 의해 결정되기 때문이다.
■ 따라서 k가 매우 클 경우, 그만큼의 공간이 추가로 필요해 비효율적일 수 있다. 이러한 이유에서 실수는 적용할 수 없다. 입력 데이터가 실수이면 k가 무한히 커지기 때문이다.



