우선순위 큐와 힙

1. 우선순위 큐(Priority Queue)

■ 우선순위 큐는 우선순위 개념을 큐에 도입한 자료구조로서 모든 데이터가 우선순위를 가진다.

■ 즉, 하나의 값만 가지는 일반적인 데이터와 달리, 우선순위 큐에 저장되는 데이터들은 값(value)과 우선순위를 동시에 가지며 입력 순서와 상관없이 우선순위가 높은 데이터가 먼저 출력된다.

■ 예를 들어 (value, priority): (A, 3), (B, 1), (C, 2), (D, 5), (E, 4)일 때, 우선순위가 높은 B, C, A, E, D 순으로 출력된다.

■ 우선순위 큐는 크게 2가지 방식으로 구현할 수 있다.

- 하나는 입력 순서대로 큐에 항목을 삽입하고, 삭제 연산이나 peek 연산을 할 때 어떤 항목이 우선순위가 높은지 찾는 것이다.- 다른 하나는 삽입 연산 시, 우선순위가 높은 순대로 정렬하는 방법이다. 이렇게 하면 삭제나 peek 연산 시, 맨 앞에 있는 값이 가장 우선순위가 높은 값이므로 맨 앞에 바로 접근해서, 맨 앞에 있는 값을 꺼내면 된다.

■ 첫 번째 방법의 핵심은 모든 항목의 우선순위 중, 우선순위가 가장 높은 것을 찾는 것이다. 첫 번째 방법을 구현하면 다음과 같다.

class PriorityQueue_1:
    def __init__(self):
        self.queue = {}
        
    def clear(self):
        self.queue = {}
    
    def is_empty(self):
        return len(self.queue) == 0
    
    def size(self):
        return len(self.queue)
        
    def enqueue(self, priority, value):
        self.queue[priority] = value
        
    def find_highest_priority(self):
        if self.is_empty():
            return None
        else:
            highest_priority = min(self.queue) # 우선순위 오름차순 기준
            return highest_priority
        
    def dequeue(self):
        highest = self.find_highest_priority()
        if highest is not None:
            return self.queue.pop(highest)
    
    def peek(self):
        highest = self.find_highest_priority()
        if highest is not None:
            return self.queue[highest]

pq_1 = PriorityQueue_1()

print(pq_1.is_empty()); print(pq_1.size())
```#결과#```
True
0
````````````

d = {3:'A', 1:'C', 2:'B', 5:'D', 4:'E'}

for key, value in d.items():
    pq_1.enqueue(key, value)
    
print(pq_1.size()); print(pq_1.find_highest_priority())
```#결과#```
5
1
````````````

print(pq_1.queue)
print('')
for _ in range(pq_1.size()):
    print(f'peek: {pq_1.peek()}, dequeue: {pq_1.dequeue()}')
    print(f'{pq_1.queue}\n')
    
```#결과#```
{3: 'A', 1: 'C', 2: 'B', 5: 'D', 4: 'E'}

peek: C, dequeue: C
{3: 'A', 2: 'B', 5: 'D', 4: 'E'}

peek: B, dequeue: B
{3: 'A', 5: 'D', 4: 'E'}

peek: A, dequeue: A
{5: 'D', 4: 'E'}

peek: E, dequeue: E
{5: 'D'}

peek: D, dequeue: D
{}
````````````````

print(pq_1.find_highest_priority())
```#결과#```
None
````````````

■ 두 번째 방법의 핵심은 삽입 연산 시, 모든 항목을 우선순위가 높은 순으로 정렬하는 것이다. 두 번째 방법을 구현하면 다음과 같다.

class PriorityQueue_2:
    def __init__(self):
        self.queue = {}
        
    def clear(self):
        self.queue = {}
    
    def is_empty(self):
        return len(self.queue) == 0
    
    def size(self):
        return len(self.queue)
        
    def enqueue(self, priority, value):
        self.queue[priority] = value
        self.queue = dict(sorted(self.queue.items())) # 우선순위 오름차순 정렬
        
    def dequeue(self):
        highest = list(self.queue.keys())[0] # 우선순위가 가장 높은 키를 가져옴
        return self.queue.pop(highest)
    
    def peek(self):
        highest = list(self.queue.keys())[0] 
        return self.queue[highest]

pq_2 = PriorityQueue_2()

for key, value in d.items():
    pq_2.enqueue(key, value)
    
print(pq_2.queue)
print('')
for _ in range(pq_2.size()):
    print(f'peek: {pq_2.peek()}, dequeue: {pq_2.dequeue()}')
    print(f'{pq_2.queue}\n')
    
```#결과#```
{1: 'C', 2: 'B', 3: 'A', 4: 'E', 5: 'D'}

peek: C, dequeue: C
{2: 'B', 3: 'A', 4: 'E', 5: 'D'}

peek: B, dequeue: B
{3: 'A', 4: 'E', 5: 'D'}

peek: A, dequeue: A
{4: 'E', 5: 'D'}

peek: E, dequeue: E
{5: 'D'}

peek: D, dequeue: D
{}
````````````

■ 첫 번째 방법의 삽입 연산은 대부분의 경우 시간 복잡도가 $O(1)$이지만, 삭제와 peek 연산은 모든 항목의 우선순위를 확인해야 하므로 $O(n)$이다.

■ 반대로 두 번째 방법의 삭제와 peek 연산은 삽입 연산에서 항목들을 우선순위가 높은 순서로 정렬해주면, 우선순위가 가장 높은 항목에 바로 접근할 수 있으므로 $O(1)$이지만, 삽입 연산은 $O(n)$이다.

■ 힙 트리를 이용하면 삽입과 삭제 연산은 $O(\log n)$, peek 연산은 $O(1)$이 소요되도록 만들 수 있다.

 

2. 힙(Heap)

■ 힙(= 힙 트리)은 자료 순서에 대한 규칙이 있는 '완전이진트리' 기반의 자료구조로서, 여러 개의 값들이 주어지면 가장 크거나 가장 작은 값을 빠르게 반환한다.

■ 힙은 이진트리 구조라서 모든 자료를 정렬할 필요 없이, 가장 큰 값을 찾을 때는 상위 레벨에 큰 값, 하위 레벨에 작은 값을

■ 가장 작은 값을 찾을 때는 작은 값들을 상위 레벨, 큰 값들을 하위 레벨에 있도록 하는 정도의 느슨한 정렬 상태를 유지한다.

■ 힙은 최대 힙(max heap)과 최소 힙(min heap)으로 나뉜다.

- 최대 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 $\text{key(부모노드)} \geq \text{key(자식노드)}$ 완전이진트리  (* 보통 특별한 언급이 없으면 힙을 최대 힙이라 가정한다.)

- 최소 힙: 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 $\text{key(부모노드)} \leq \text{key(자식노드)}$ 완전이진트리

- 즉, 최대 힙에서는 루트 노드에 저장된 자료의 우선순위 중에서 가장 큰 값이,

- 최소 힙에서는 키 값 중 가장 작은 값이 루트 노드에 오도록 만들어진다.

■ 따라서 우선순위의 값이 큰 순서대로 처리가 되도록 하고자 할 때는 최대 힙

■ 반대로, 우선순위의 값이 작은 순서대로 처리가 되도록 하고자 할 때는 최소 힙을 이용한다.

■ 위와 같이 힙이 되기 위한 조건은 ① 완전이진트리 ② 부모와 자식 노드의 키(key) 값 간의 크기이다.

■ 예를 들어 다음 트리는 완전이진트리 구조이며, 부모 노드들의 키 값이 자식 노드들의 키 값보다 크거나 같은 값을 가지므로 최대 힙이다.

■ 다음 트리는 완전이진트리 구조이며, 부모 노드들이 자식 노드들보다 키 값이 작거나 같으므로 최소 힙이다.

■ 다음 트리는 부모 노드들의 키 값이 자식 노드들의 키 값보다 크거나 같으므로 최대 힙처럼 보이지만, 완전이진트리 구조가 아니므로 최대 힙이라 할 수 없다.

■ 다음 트리는 부모의 키 값이 8, 왼쪽 자식의 키 값은 10, 오른쪽 자식의 키 값은 7이다. 부모 노드가 자식 노드의 키 값보다 작은 경우도 있고 큰 경우도 있다. 이런 경우 완전이진트리 구조여도 힙이 될 수 없다.

2.1 힙의 연산

■ 힙은 가장 우선순위가 높은 항목이 루트 노드에 있으므로 접근 연산은 단순히 루트 노드에 접근하면 된다.

■ 힙의 삽입 & 삭제 연산은 삽입이나 삭제 후 힙이 유지될 수 있도록, 힙의 조건 2 가지 ① 완전이진트리 ② 부모 노드와 자식 노드의 키 값 간의 특성( $\text{key(부모노드)} \geq \text{key(자식노드)}$ 또는 $\text{key(부모노드)} \leq \text{key(자식노드)}$)을 만족시키도록 구현해야 한다.

2.1.1 힙의 삽입 연산

■ 힙에 새로운 항목을 삽입하더라도 

- ① 완전이진트리의 조건이 만족되도록 새로운 노드를 삽입해야 하고

- ② 부모 노드와 자식 노드의 크기 조건이 만족되도록 원소(노드)의 위치를 조정해야 한다.

■ 따라서 삽입 방법은 ① (마지막 레벨에서의) 마지막 노드의 다음 위치에 새로운 항목을 삽입한다. 이렇게 하면 완전이진트리의 조건은 만족한다.

■ 그 다음으로 ② 삽입된 데이터와 삽입된 데이터의 부모 노도를 비교해서 부모 노드와의 크기 조건( $\text{key(부모노드)} \geq \text{key(자식노드)}$ 또는 $\text{key(부모노드)} \leq \text{key(자식노드)}$)을 만족하도록 삽입된 데이터의 위치를 조정한다.

■ 이 이동은 리프 노드에서 루트 노드까지 비교해가며 이동할 수 있다. 즉, 최악의 경우 힙의 높이에 해당하는 비교 연산 및 이동 연산이 필요하다. 

■ 힙은 완전이진트리이므로 노드의 개수가 $n$이면 힙의 높이는 $\log_2 n$이다. 따라서 최악의 경우 삽입 연산의 시간 복잡도는 $O(\log_2 n)$, 즉 $O(\log n)$이다.

■ 삭제 연산도 동일한 방식이라서 힙의 삽입, 삭제 연산의 시간 복잡도는 최악의 경우 $O(\log n)$이다.

■ 예를 들어 다음과 같은 최대 힙에 9를 삽입한다면

- 1) 먼저, 완전이진트리의 조건이 만족되도록 완전이진트리의 마지막 노드 '3' 다음 위치에 '9'를 삽입한다.

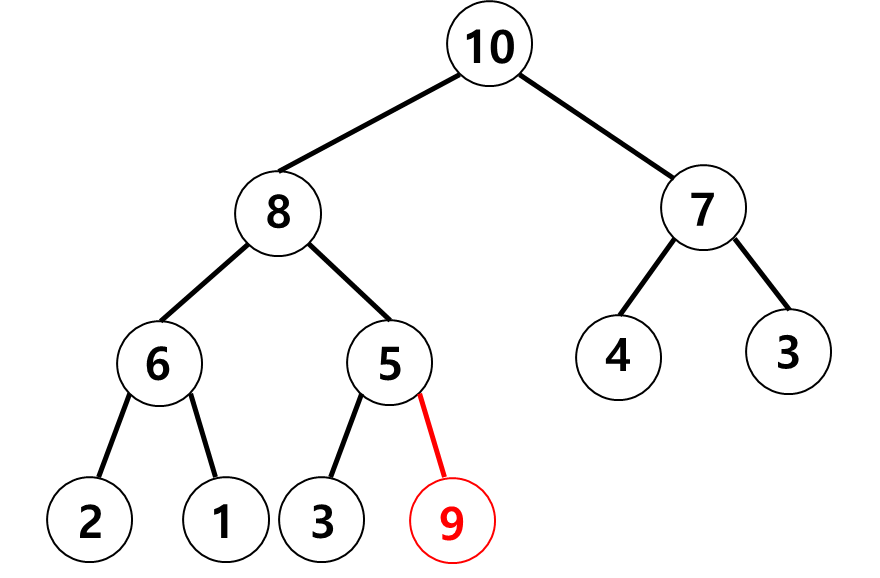
이렇게 되면 완전이진트리의 조건은 만족하지만, 부모 노드와의 크기 조건이 만족되지 않아 최대 힙을 만족하지 않는다. 따라서 부모 노드와 크기를 비교해가며 최대 힙이 성립되도록 노드 '9'의 위치를 이동시켜야 한다.

-2) '9'의 부모 노드인 '5'와 비교했을 때, 삽입된 노드 '9'가 더 크므로 노드 '5'와 '9'의 위치를 교환한다.

-3) 아직 부모와의 크기 조건이 만족되지 않았으므로, 현재 '9'의 부모 '8'과 비교한다. '9'가 더 크므로 '8'과 위치를 교환한다.

-4) 현재 '9'의 부모 '10'과 비교했을 때, 부모가 더 크므로 더 이상 교환하지 않는다.

■ 이렇게 이동이 끝났을 때를 보면 '9'가 삽입되더라도 최대 힙이 되는 것을 볼 수 있다. 

■ 삽입 연산 시, 이러한 이동을 시프트 업(sift up) 또는 업 힙(up heap)이라고 한다.

 

2.1.2 힙의 삭제 연산

■ 힙의 삭제 연산은 항상 루트 노드를 삭제하며 루트 노드의 값(최댓값 혹은 최솟값)을 반환해야 한다.

■ 따라서 삭제 방법은 ① 루트 노드가 삭제되면 마지막 노드를 루트 노드 자리로 옮겨 완전이진트리 형태를 유지시킨다.  

■ 그 다음으로 ② 새로운 루트 노드(기존의 마지막 노드)와 자식 노드들과의 크기 조건이 만족되도록 위치를 이동한다.

■ 이때의 이동을  시프트 다운(sift down) 또는 다운 힙(down heap)이라고 한다.

■ 예를 들어 다음과 같은 최대 힙에 삭제 연산을 적용한다면

- 1) 먼저, 루트 노드가 삭제되고, 마지막 노드를 루트 노드 자리로 옮긴다.

이렇게 되면 완전이진트리 조건은 만족되지만, 부모와 자식 간의 크기 조건이 만족되지 않아 최대 힙을 만족하지 않는다.

- 2) 루트 노드 '3'과 자식 노드 '6', '7' 중 '7'이 가장 크므로 '3'과 '7'의 자리를 교환한다. 이렇게 되면 루트 '7', 자식은 '3', '6'이라 이 부분은 최대 힙이 성립한다.

- 3) 그 다음으로 '3'과 '3'의 자식 '5', '4' 중 다른 자식보다 더 큰 '5'와 자리를 교환한다. 그러면 이 부분도 최대 힙이 성립한다.

- 4) '3'과 자식 '2', '1'을 비교했을 때, 이 부분은 이미 최대 힙이 성립하므로 이동이 끝난다. 이렇게 이동이 끝났을 때 최대 힙이 되는 것을 볼 수 있다.

■ 삭제 연산은 최악의 경우 루트 노드에서 리프 노드까지 비교해 가면서 이동해야 한다. 따라서 삭제 연산도 삽입 연산처럼 시간 복잡도 $O(\log n)$이다.

 

2.2 힙의 구현

■ 힙은 완전이진트리이기 때문에 중간에 비어 있는 노드가 없으므로 각 노드에 인덱스를 부여해서 사용한다면 배열 구조에 힙의 노드들을 저장할 수 있다.

■ 배열 구조를 사용하면 삽입이나 삭제 연산 과정에서 인덱스 계산으로 부모 노드와 자식 노드의 위치를 간단하게 계산할 수 있으므로 힙을 배열에 저장하는 것이 효과적이다.

■ 예를 들어 다음과 같은 힙을 배열에 저장한다면, (루트 노드 번호 1부터 시작, 인덱스 0은 계산 편의를 위해 사용하지 않음)

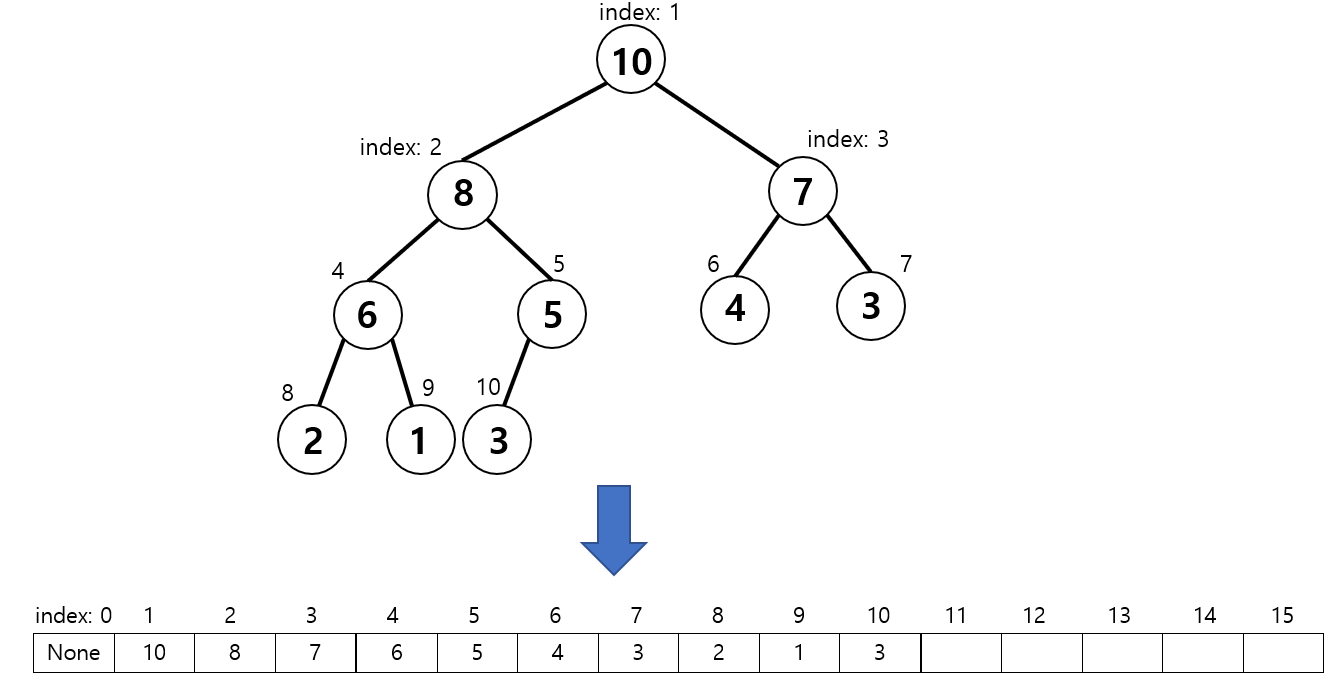
- 노드 $i$의 부모 인덱스는 $i // 2$

- 노드 $i$의 왼쪽 자식 노드의 인덱스는 $2i$

- 노드 $i$의 오른쪽 자식 노드의 인덱스는 $2i + 1$

2.2.1 최대 힙 구현

■ 첫 번째 자리(0번 인덱스)는 비우고 두 번째 자리(1번 인덱스)부터 힙이 배열 구조인 리스트에 저장되도록 생성자 메소드를 다음과 같이 정의할 수 있다.

class MaxHeap:
    def __init__(self):
        self.heap = [None]

■ 위와 같이 self.heap = [None]으로 설정하면 MaxHeap 클래스의 새로운 객체를 만들 때, 0번 인덱스는 None 값이 들어가므로 힙이 저장될 때 1번 인덱스에는 전체 트리의 루트 노드가 저장된다. 

■ 따라서 힙의 크기를 확인할 때는 self.heap 리스트의 길이에서 1을 빼주어야 한다.

■ 그러므로 공백 검사는 힙의 크기를 확인하는 메소드를 클래스의 객체에 적용했을 때 값이 0인지 확인하면 된다.

■ 또한 힙의 내용을 확인할 때, None을 출력하지 않도록 리스트의 슬라이싱 기법을 사용해 1번 인덱스부터 힙의 내용을 확인해야 하며, 초기화 메서드는 빈 리스트가 아닌 0번 인덱스에 None이 있는 리스트로 초기화되도록 설정해야 한다.

■ 마지막으로 노드가 $i$일 때, 부모 노드와 왼쪽 & 오른쪽 자식 노드를 찾는 인덱스 계산도 0번 인덱스에는 접근하지 못하도록 다음과 같이 설정해야 한다.

class MaxHeap:
    def __init__(self):
        self.heap = [None]
        
    def size(self):
        return len(self.heap) - 1
    
    def is_empty(self):
        return self.size() == 0
    
    def display(self):
        print(self.heap[1: ])
        
    def clear(self):
        self.heap = [None]    
        
    def parent(self, i):
        if i == 0 or i == 1:
            raise Exception('There is no parent node')
        else:
            return self.heap[i//2]
    
    def left(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:
            return self.heap[2*i]
    
    def right(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:        
            return self.heap[2*i+1]

■ 삽입 연산은 먼저, 맨 마지막 노드 다음 위치에 새로운 노드를 삽입하고, 삽입된 노드가 몇 번 인덱스인지 확인해야 한다. 그래야 부모 노드의 인덱스를 계산해서 부모 노드를 찾고 비교할 수 있기 때문이다.

- 부모 노드와 비교는 삽입된 노드가 루트 노드가 되거나, 즉 1번 인덱스까지 올라가거나 부모 노드의 값과 비교했을 때 삽입된 노드의 값이 부모 노드보다 작거나 같으면 더 이상 이동할 필요가 없으므로 업 힙을 종료해야 한다.

- 이런 종료 조건이 만족될 때까지 부모 노드와 자리를 교환해야 하는데, 교환은 삽입된 노드의 인덱스를 부모 노드의 인덱스로 갱신하면 된다.

- 그리고 이동이 끝난 최종 자리의 인덱스에 삽입한 노드의 값을 넣어주면 삽입 연산은 끝나게 된다.

def insert(self, node):
    self.heap.append(node) # 맨 마지막 위치에 새로운 노드 삽입
    i = self.size() # 삽입 후 리스트의 크기, 즉 새로운 노드의 인덱스를 i로 설정
    while True:
        if i == 1 or node <= self.parent(i): # 삽입된 노드가 루트 노드까지 올라가거나, 
            break  # 삽입된 노드의 값이 부모 노드보다 작거나 같으면 이동을 멈춘다.
        self.heap[i] = self.parent(i) # 그렇지 않으면 부모 노드를 끌어내리고
        i = i//2 # 새로운 노드의 인덱스를 부모 노드의 인덱스로 올린다.
    self.heap[i] = node # 이동이 끝나면 최종 자리의 인덱스에 삽입한 노드의 값을 넣어주면 삽입 연산은 종료

■ 삭제 연산은 루트 노드를 삭제하고 마지막 위치의 노드를 루트 노드 자리에 옮겨 다운 힙을 진행한다.

- 새로운 루트 노드(기존의 마지막 위치의 노드)의 왼쪽 자식과 오른쪽 자식을 비교하는데, 최대 힙에서의 삭제 연산은 왼쪽과 오른쪽 중 더 값이 큰 자식 노드와 위치를 교환하고 자식 노드의 값보다 크거나 같으면 이동을 멈춘다.

- 위치 교환은 부모 노드와 자식 노드 값을 비교해 자식 노드가 더 큰 값을 가지면 자식을 부모 위치로, 부모를 자식 위치로 바꾸면 된다.

- 위치 교환이 끝나면 최종 위치에 루트 노드로 올렸던 노드의 값을 넣어주면 된다. 그리고 삭제한 루트 노드의 값을 반환하면 삭제 연산은 끝나게 된다.

def delete(self):
    if self.is_empty():
        raise Exception('Heap is empty')
        
    root, last = self.heap, self.heap[self.size()] # 반환할 루트 노드와, 삭제할 루트 노드 자리로 옮길 마지막 노드를 저장
    self.heap.pop(-1) # 마지막 노드 삭제
    
    i, j = 1, 2 # i는 이동해야 하는 새로운 루트 노드의 인덱스, j는 그 자식 노드의 왼쪽 자식 인덱스라고 한다면
    while True:
        if j > self.size(): # 힙의 크기가 1, 즉 자식 노드가 없는 리프 노드라면 
            break # 이동할 필요가 없으니 종료
         
        if j+1 <= self.size(): # 힙의 크기가 2, 즉 루트 노드와 왼쪽 자식 노드로만 구성된 트리가 아닌, 오른쪽 자식이 있는 형태라면
            if self.left(i) < self.right(i): # 새로운 루트 노드의 왼쪽 자식과 오른쪽 자식의 크기를 비교해서
                j += 1 # 오른쪽 자식의 값이 더 크다면 j를 오른쪽 자식의 인덱스로 갱신, 그렇지 않다면 j는 그대로 왼쪽 자식의 인덱스
        
        if last >= self.heap[j]: # 새로운 루트 노드의 값이 왼쪽 자식(j = 2) 또는 오른쪽 자식(j = 3)보다 크다면
            break # 이동할 필요가 없으니 종료
            
        self.heap[i] = self.heap[j] # i = 1이고 j = 2 or j = 3인 상태이므로 부모 노드와 자식 노드의 값을 교환
        i = j # 이제 i는 2 or 3이 되고 
        j = 2*i # j는 인덱스 2 노드의 왼쪽 자식 인덱스 4 or 인덱스 3 노드의 왼쪽 자식 노드의 인덱스가 되고 while 문을 반복해 i와 j값을 갱신한다.
    self.heap[i] = last # 최종 위치에 도달하면 해당 위치(인덱스)에 last 값을 넣는다.
    return root

 

- 위와 같은 기능들을 종합하면 최대 힙의 클래스는 다음과 같다.

class MaxHeap:
    def __init__(self):
        self.heap = [None]
        
    def size(self):
        return len(self.heap) - 1
    
    def is_empty(self):
        return self.size() == 0
    
    def display(self):
        print(self.heap[1: ])
        
    def clear(self):
        self.heap = [None]    
        
    def parent(self, i):
        if i == 0 or i == 1:
            raise Exception('There is no parent node')
        else:
            return self.heap[i//2]
    
    def left(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:
            return self.heap[2*i]
    
    def right(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:        
            return self.heap[2*i+1]
        
    def insert(self, node):
        self.heap.append(node) 
        i = self.size() 
        while True:
            if i == 1 or node <= self.parent(i): 
                break  
            self.heap[i] = self.parent(i) 
            i = i//2 
        self.heap[i] = node 
        
    def delete(self):
        if self.is_empty():
            raise Exception('Heap is empty') 
        root, last = self.heap, self.heap[self.size()] 
        self.heap.pop(-1) 
        i, j = 1, 2 
        while True:
            if j > self.size(): 
                break 
         
            if j+1 <= self.size(): 
                if self.left(i) < self.right(i): 
                    j += 1 
        
            if last >= self.heap[j]: 
                break 
            self.heap[i] = self.heap[j] 
            i = j 
            j = 2*i 
        self.heap[i] = last 
        return root

mh = MaxHeap()
mh.heap
```#결과#```
[None]
````````````

for i in [10,8,7,6,5,4,3,2,1,3]:
    mh.insert(i)
    
mh.heap
```#결과#```
[None, 10, 8, 7, 6, 5, 4, 3, 2, 1, 3]
````````````

mh.left(0) # 0번 인덱스는 None
```#결과#```
---------------------------------------------------------------------------
Exception                                 Traceback (most recent call last)
Cell In[11], line 1
----> 1 mh.left(0)

Cell In[5], line 25, in MaxHeap.left(self, i)
     23 def left(self, i):
     24     if i == 0:
---> 25         raise Exception('There is no node 0')
     26     else:
     27         return self.heap[2*i]

Exception: There is no node 0
`````````````

mh.parent(1) # 1번 인덱스부터 시작하므로 1번 노드의 부모 노드는 없다.
```#결과#```
---------------------------------------------------------------------------
Exception                                 Traceback (most recent call last)
Cell In[12], line 1
----> 1 mh.parent(1)

Cell In[5], line 19, in MaxHeap.parent(self, i)
     17 def parent(self, i):
     18     if i == 0 or i == 1:
---> 19         raise Exception('There is no parent node')
     20     else:
     21         return self.heap[i//2]

Exception: There is no parent node
``````````````

mh.display()
```#결과#```
[10, 8, 7, 6, 5, 4, 3, 2, 1, 3]
````````````

mh.insert(9) # 삽입 연산
mh.display()
```#결과#```
[10, 9, 7, 6, 8, 4, 3, 2, 1, 3, 5]
````````````

mh.clear()

for i in [9,7,6,5,4,3,2,2,1,3]:
    mh.insert(i)
    
mh.delete() # 삭제 연산
```#결과#```
[None, 7, 5, 6, 3, 4, 3, 2, 2, 1]
````````````

mh.display()
```#결과#```
[7, 5, 6, 3, 4, 3, 2, 2, 1]
````````````

print(mh.parent(2), mh.left(2), mh.right(2)) # 인덱스 2인 노드 5의 부모 노드와 자식 노드들
```#결과#```
7 3 4
````````````

 

2.2.2 최소 힙 구현

■ 최소 힙의 삽입, 삭제 연산은 최대 힙과 반대로 부모 노드가 자식 노드보다 작거나 같을 때, 위치 이동을 종료시키면 된다.

class MinHeap:
    def __init__(self):
        self.heap = [None]
        
    def size(self):
        return len(self.heap) - 1
    
    def is_empty(self):
        return self.size() == 0
    
    def display(self):
        print(self.heap[1: ])
        
    def clear(self):
        self.heap = [None]    
        
    def parent(self, i):
        if i == 0 or i == 1:
            raise Exception('There is no parent node')
        else:
            return self.heap[i//2]
    
    def left(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:
            return self.heap[2*i]
    
    def right(self, i):
        if i == 0:
            raise Exception('There is no node 0')
        else:        
            return self.heap[2*i+1]
        
    def insert(self, node):
        self.heap.append(node) 
        i = self.size() 
        while True:
            if i == 1 or node >= self.parent(i): 
                break  
            self.heap[i] = self.parent(i) 
            i = i//2 
        self.heap[i] = node 
        
    def delete(self):
        if self.is_empty():
            raise Exception('Heap is empty') 
        root, last = self.heap, self.heap[self.size()] 
        self.heap.pop(-1) 
        i, j = 1, 2 
        while True:
            if j > self.size(): 
                break 
         
            if j+1 <= self.size(): 
                if self.left(i) > self.right(i): 
                    j += 1 
        
            if last <= self.heap[j]: 
                break 
            self.heap[i] = self.heap[j] 
            i = j 
            j = 2*i 
        self.heap[i] = last 
        return root

min_h = MinHeap()
for i in [1,4,2,6,5,3,3,8,9,10]:
    min_h.insert(i)
    
min_h.heap
```#결과#```
[None, 1, 4, 2, 6, 5, 3, 3, 8, 9, 10]
````````````

min_h.display()
```#결과#```
[1, 4, 2, 6, 5, 3, 3, 8, 9, 10]
````````````

min_h.insert(3)
min_h.display()
```#결과#```
[1, 3, 2, 6, 4, 3, 3, 8, 9, 10, 5]
````````````

min_h.clear()

for i in [1,2,4,6,5,7,8,9]:
    min_h.insert(i)
    
min_h.delete()
```#결과#```
[None, 2, 5, 4, 6, 9, 7, 8]
````````````

min_h.display()
```#결과#```
[2, 5, 4, 6, 9, 7, 8]
````````````

 

2.3 우선순위 큐의 가장 좋은 구현 방법은 힙

■ 정렬되지 않은 배열로 우선순위 큐를 구현할 경우, 우선순위가 가장 높은 항목을 찾기 위해 모든 항목의 우선순위를 비교하므로 탐색 연산의 시간 복잡도는 $O(n)$ 이었다. 또한, 삭제 연산도 우선순위가 가장 높은 항목을 찾아 반환시켜야 해서, 삭제 연산의 시간 복잡도도 $O(n)$ 이었다. 이렇게 탐색, 삭제 연산을 할 때만 가장 높은 우선순위 항목을 찾기 때문에 삽입 연산 시에는 단순히 배열의 맨 마지막에 새로운 항목을 추가하기만 하면 되기 때문에 삽입 연산의 시간 복잡도는 $O(1)$ 이었다.

■ 우선순위대로 정렬된 배열을 사용할 경우는 삭제 연산 시, 우선순위에 따라 삽입할 위치를 찾아야 해서 최악의 경우, 전체 항목을 비교해야 하며 삽입할 위치를 찾더라도 항목을 삽입하기 위해 항목의 이동이 필요했다. 이렇게 정렬된 배열을 이용하면 삽입 연산의 시간 복잡도는 $O(n)$ 이었다. 그러나 배열을 정렬할 경우 우선순위가 높은 것을 찾는 탐색 연산이나 삭제 연산은 우선순위가 가장 높은 항목의 위치에 바로 접근해서 연산을 수행할 수 있기 때문에 시간 복잡도는 $O(1)$ 이었다. 우선순위가 가장 높은 항목이 배열 맨 뒤에 있으면, 항목을 이동시킬 필요 없이 맨 뒤에 접근하여 연산을 수행하면 되기 때문이다.

■ 힙으로 우선순위 큐를 구현할 경우 삽입 & 삭제 연산 시, 최악으기 경우여도 시간 복잡도는 $O(\log_2 n)$이고 탐색 연산의 경우, 힙은 우선순위가 높은 항목이 루트 노드에 있으므로 단순히 루트 노드를 반환하면 되기 때문에 시간 복잡도는 $O(1)$ 이었다.

■ 이렇게 힙을 이용하면 최악의 경우라도 $O(\log_2 n)$ 시간이 보장되므로, 우선순위 큐를 구현하는 가장 좋은 방법은 힙이다.

 

2. 파이썬 heapq 모듈

■ heapq 모듈은 리스트를 최소 힙으로 변경하는 heapify( ) 함수를 지원한다.

import heapq

arr = [9,7,6,5,4,3,2,2,1,3]
heapq.heapify(arr) # 리스트를 최소 힙으로 
arr
```#결과#```
[1, 2, 2, 5, 3, 3, 6, 7, 9, 4]
````````````

heap = []
for i in [1,4,2,6,5,3,3,8,9,10]:
    heapq.heappush(heap, i) # heapq.heappush는 최소 힙 삽입 연산
heap
```#결과#```
[1, 4, 2, 6, 5, 3, 3, 8, 9, 10]
````````````

heapq.heappush(heap, 3)
heap
```#결과#```
[1, 3, 2, 6, 4, 3, 3, 8, 9, 10, 5]
````````````

heap = []
for i in [1,2,4,6,5,7,8,9]:
    heapq.heappush(heap, i) 
heapq.heappop(heap) # 최소 힙 반환 & 삭제 연산
heap
```#결과#```
[2, 5, 4, 6, 9, 7, 8]
````````````

heap2 = []
for i in [1,4,2,6,5,3,3,8,9,10]:
    heapq.heappush(heap2, i) 
    
heap2
```#결과#```
[1, 4, 2, 6, 5, 3, 3, 8, 9, 10]
`````````````

heapq._heapify_max(heap2) # 최대 힙으로 변환
heap2
```#결과#```
[10, 9, 3, 8, 5, 3, 2, 1, 6, 4]
`````````````