1. 디지털 이미지 처리기법에서의 특이값 분해 응용
■ 디지털 이미지는 픽셀이라는 격자에 색을 칠하여 어떤 문자나 그림을 표현하는 것으로 생각할 수 있다.
■ 컬러 이미지는 Red, Green, Blue. 총 3개의 채널로 표현되며, 각 채널은 0~255 사이의 값으로 빨강, 초록, 파랑의 정도를 나타낸다.
■ 흑백 이미지(그레이 스케일 이미지)는 1개의 채널로 표현되며, 각 픽셀의 밝기 값을 0~255 사이의 값으로 표현한다.
■ 흑백 이미지는 회색 음영을 검은색부터 흰색까지 총 256단계로 나누어 표현한다. 즉, 256가지 정보를 표현하기 위해서는 \( 256 = 2^8 \)이므로 흑백 이미지는 한 픽셀마다 8 bit = 1 byte가 필요하다.
- 컬러 이미지는 채널이 3개이며, 각 채널마다 256개의 빨강, 초록, 파랑의 정도를 나타내므로, \( 256^3 = 16,777,216 \)가지 색을 만들어 낼 수 있다.
■ 각 픽셀이 오직 흰색(1)과 검은색(0)으로 표현되는 이미지를 바이너리(binary) 이미지라고 부른다. 바이너리 이미지는 0과 1만 2가지 정보만 표현하므로 \( 2^1 = 2 \)이다. 즉, 한 픽셀당 1bit가 필요하다.
■ 이러한 디지털 이미지들은 모두 숫자로 표시되며, 특히 그레이 스케일 이미지로 디지털 이미지를 읽어 들이면 두 개의 축을 갖는 배열. 즉, 행렬의 형태가 된다.
■ 이렇게 행렬의 형태를 갖는 이미지에 행렬에서 사용하는 다양한 연산을 수행할 수 있다. 단순하게는 픽셀의 값(행렬의 원소의 값)을 조정하는 것부터 이렇게 특이값 분해를 이용하여 이미지의 노이즈를 감소시키거나 압축 효과를 볼 수 있다.
1.1 노이즈(noise) 감소
■ 흑백(그레이 스케일) 이미지의 밝기 값 0~255 사이의 값을 255로 정규화하면 검은색은 0 = 0 /255, 흰색은 1 = 255/255로 표현된다.
■ 픽셀 크기가 \( m \times n \)인 흑백 이미지의 밝기 값을 정규화(255로 나누기)하면, 이미지의 각 성분의 값은 \( k /256, \; (0 \leq k \leq 255) \)인 \( m \times n \) 행렬로 이해할 수 있다.
■ 그러므로 픽셀 크기가 \( m \times n \)인 그레이 스케일 이미지를 전송한다면, \( m \times n \times 1 \)byte = \( mn \)byte의 데이터를 전송한다.
■ 이렇게 전송하는 과정에서 이미지에 노이즈가 생길 수 있다. 이런 노이즈를 제거하기 위해 행렬로 표현된 이미지에 특이값 분해를 응용할 수 있다.
■ 예를 들어, 픽셀의 크기가 \( m \times n \)인 이미지를 스캔하는 과정에서 이미지에 노이즈가 생겼다고 하자.
- 이미지에 노이즈가 생기면 다음 그림과 같이 된다. 왼쪽은 원래 이미지, 오른쪽은 노이즈가 추가된 이미지이다.
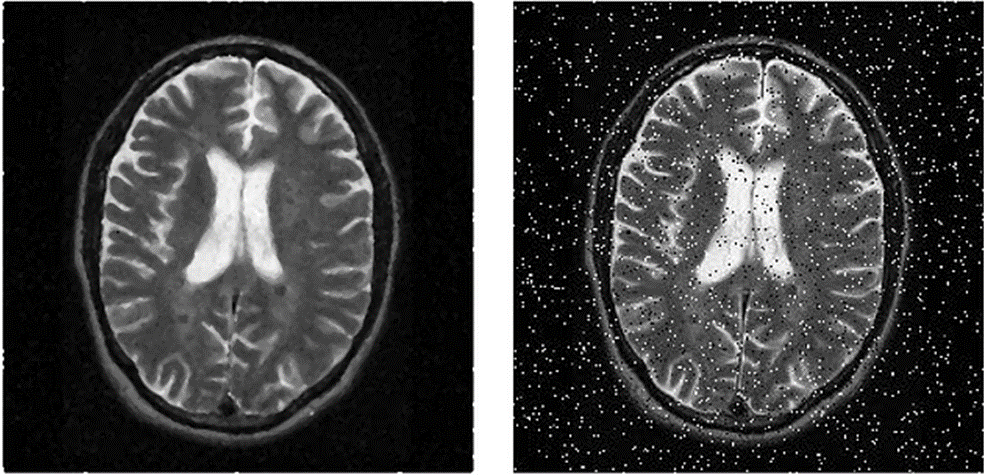
■ 노이즈가 추가된 이미지가 \( m \times n \) 행렬 \( A \)라고 하자. 이 행렬 \( A \)에 대하여 특이값 분해를 하면 \( A = U \Sigma V^T \)로 나타낼 수 있고, 여기서 대각행렬인 \( \Sigma \) 행렬의 대각 원소에 있는 특이값은 이 이미지 데이터에 대한 정보(ex) 분산)를 나타낸다.
■ 그리고 \( \Sigma \) 행렬의 대각 원소에 있는 특이값은 순서대로 \( \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0 \)이다.
■ 즉, 특이값 \( \sigma_1, \sigma_2, \cdots, \sigma_r \)에는 이 이미지에 대한 정보가 들어 있는데, 대각행렬 \( \Sigma \) 왼쪽 위에서부터 순서대로 위치한 특이값들은 다른 특이값들에 비해 많이 들어있을 것이다.
■ 노이즈 감소는 바로 이러한 특이값의 특징을 이용한다. 정확하게는, 노이즈가 추가된 이미지 행렬 \( A \)를 계수가 1인 행렬들로 근사시키되, \( \displaystyle \sum^{3}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \)처럼 특이값 중 상위 일부 데이터만 추출해 근사시키는 것이다. 즉, Truncated SVD를 이용하는 것이다.
■ 위의 노이즈가 낀 뇌 이미지에는 원래 '뇌' 이미지에 '노이즈' 데이터가 추가된 것으로 볼 수 있다. 이때, 이 뇌 이미지에서 중요한 것은 '뇌'이다.
■ 뇌 이미지에서 중요한 '뇌'를 나타내기 위한 정보를 가장 많이 가지고 있는 것은 가장 큰 특이값인 \( \sigma_1 \)이고, \( \sigma_1 \)외에 '뇌'를 최대한 나타낼 수 있는 정보를 가지고 있는 특이값들은 \( \sigma_1 \)에 가까운 특이값들이 된다.
■ 반대로 '노이즈'에 대한 정보를 가지고 있는 특이값은 \( \sigma_r \)에 가까운 특이값들일 것이라고 생각할 수 있다.
■ 그래서 최대한 이미지에 노이즈를 반영하지 못하도록 \( \displaystyle \sum^{3}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \)처럼 특이값 중 상위 일부 데이터만 추출해 근사시키는 것이다.
- \( \mathbf{u}_i \)는 \( i \) 번째 왼쪽 특이벡터, \( \mathbf{v}^T_i \)는 \( i \) 번째 오른쪽 특이벡터, \( \sigma_i \)는 \( i \) 번째 특이값.
■ 그리고 경우에 따라 특이값 중 상위 일부 데이터만 추출해서 이미지를 근사했을 때, 원래 이미지를 잘 나타내면서 노이즈가 어느 정도 제거될 수도 있고, 그렇지 않을 수도 있다.
■ 또한 노이즈 완화 정도가 사용자의 기준에 따라 다르다. 그러므로 \( \displaystyle \sum^{3}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \; \), \( \displaystyle \sum^{4}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \; \), \( \displaystyle \sum^{5}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \; \), \( \cdots \) \( \displaystyle \sum^{r-k}_{i=1} \mathbf{u}_i \sigma_i \mathbf{v}^T_i \) \( \cdots \)처럼 여러 번 확인하여 사용자가 원하는 상태의 이미지를 선택하면 된다.
1.2 데이터 압축효과
■ 픽셀 크기가 \( m \times n \)인 그레이 스케일 이미지를 저장하는데는 \( mn \)byte가 필요하다. 그리고 이미지를 저장하는 경우가 아니더라도 데이터의 용량을 줄여야 하는 경우들이 있다. 이러한 크기 문제도 행렬의 특이값 분해를 이용하여 해결할 수 있다.
■ 계수(rank)가 \( r \)인 \( m \times n \) 행렬 \( A \)의 특이값 분해는 다음과 같이 나타낼 수 있다.
\( A = U \; \Sigma \; V^T \Leftrightarrow \displaystyle \sum^{r}_{i=1} \mathbf{u}_i \; \sigma_i \; \mathbf{v}^T_i, \quad ( \sigma_1 \geq \sigma_2 \geq \cdots \geq \sigma_r > 0) \)
■ 이때, 계수가 \( k \)인 행렬을 \( B \)라고 하자. \( ( 1 \leq k \leq r ) \)
■ 이 행렬 \( B \)는 \( B = \displaystyle \sum^{k}_{i=1} \mathbf{u}_i \; \sigma_i \; \mathbf{v}^T_i \)로 나타낼 수 있다.
■ 이 행렬 \( B \)는 원본 이미지를 나타낸 행렬 \( A \)에 근사하는 행렬이다. 즉, 행렬 \( B \)도 하나의 이미지이다.
■ 이때, \( B \)를 저장하는데 필요한 바이트 수는 \( 1 \leq i \leq k \)에 대해 \( i \) 번째 왼쪽 및 오른쪽 특이벡터 \( \mathbf{u}_i \)와 \( \mathbf{v}^T_i \) 그리고 \( i \) 번째 특이값 \( \sigma_i \)를 각각 저장하는데 필요한 바이트 수와 같다.
■ 왼쪽 특이벡터와 오른쪽 특이벡터인 \( \mathbf{u}_i \)와 \( \mathbf{v}^T_i \)는 행렬 \( B \)의 4개의 부분공간 중 어떤 공간에 대한 '정규직교기저'이다. 즉, 단위벡터이다.
■ 단위벡터의 경우, 각 성분(원소)를 표현하는데 1 byte씩 필요하다. 그러므로 \( 2k \)개의 벡터를 저장하는데 \( k(m+n) \)byte가 필요하다. 그리고 각 특이값을 저장하는데는 4byte면 충분하다.
■ 만약, 이미지를 저장하는데 사용할 수 있는 바이트 수가 \( M \)이라면, \( k(m+n+4) < M \)을 만족하는 \( k \)중 최댓값인 \( k \)를 선택하여 계수가 \( k \)인 행렬에 대한 이미지를 근사 이미지로 사용하면 된다.
■ 예를 들어 \( 500 \times 400 \) 크기의 그레이 스케일 이미지가 있다고 할 때, 이 이미지를 행렬로 표현했을 때, 행렬의 계수(rank)가 400이라고 하자.
■ 이 이미지를 저장하는데 필요한 바이트 수는 \( 600 \times 400 \)byte \( = 240000 \)byte이다.
■ 만약, 계수 \( k = 100 \)인 행렬로 근사시킨 경우에 각 특이값을 저장하는데 1byte면 충분하다. 그러므로 \( k = 100 \)인 행렬로 근사시킨 이미지를 저장하기 위해 필요한 바이트 수는 \( 100(600+400+1) = 100100 \)byte이다.
■ 즉, \( k = 100 \)인 행렬로 근사시킨 이미지를 사용하면, 원래 이미지를 저장하는데 필요한 바이트 수의 약 41.7% 정도만으로 원래 이미지와 유사한 결과를 얻을 수 있다.
■ 1.1의 잡음(noise) 제거와 1.2의 데이터 압축은 모두 SVD를 통한 낮은 계수 근사를 이용한다.
■ 차이점은, 압축 효과는 저장 공간을 절약하기 위해 중요한(= 큰) 특이값만 보존한다. 작은 특이값은 저장 공간을 절약하기 위해 제거할 수 있는 덜 중요한 정보로 간주한다.
■ 잡음 제거의 경우 (이미지) 데이터 행렬에 잡음을 생기게 하는 SVD 구성 요소를 제거하는데. 이때 제거할 구성 요소는 가장 작은 특이값과 관련된 것일 수도 있지만, 더 큰 특이값이 잡음의 주요 원인이 될 수도 있다.
- 제거할 구성 요소는 사용자가 직접 확인하여 식별할 수 있다.
2. 잠재 의미 분석 (Latent Semantic Analysis, LSA)
■ BoW에 기반한 DTM이나 TF-IDF는 단어의 빈도수를 이용한 방법으로 단어의 의미를 고려하지 못한다는 단점이 있다.
■ 이를 위한 대안으로 DTM의 잠재된 의미를 이끌어내는 방법으로 잠재 의미 분석(Latent Semantic Indexing, LSI)이라고 부르기도 한다.
■ LSA 알고리즘은 토픽 모델링(Topic Modeling) 분야의 시초가 되는 알고리즘이다.
■ 토픽 모델은 문서 집합의 추상적인 토픽. 즉, '주제'를 발견하기 위해 텍스트에 숨겨진 의미구조를 발견하기 위해 사용되는 튱계적 모델이다.
■ 이 방법을 이해하기 위해서는 선형대수의 특이값 분해(SVD)의 변형에 대해 이해할 필요가 있다.
2.1 특이값 분해의 변형
■ \( m \times n \)행렬 \( A \)의 계수(rank)가 \( r \)이며, \( A = U \Sigma V^T \)에서 \( U \)는 \( m \times m \), \( \Sigma \)는 \( m \times n \), \( V^T \)는 \( n \times n \)인 상태라고 하자.
■ \( A = U \Sigma V^T \)를 그대로 유지한 형태를 full SVD라고도 부른다.
2.1.1 Thin SVD
■ thin SVD는 대각행렬 \( \Sigma \)에서 대각 원소 \( \sigma_r \)의 아랫 부분과 \( U \)에서 이에 대응하는 열을 제거한 형태를 말한다.
■ 즉, \( m \times n \) 대각행렬 \( \Sigma \)에서 비대각 원소를 모두 제거하여 \( n \times n \) 크기의 \( \Sigma \)로 만들고, 이에 대응하는 왼쪽 특이벡터들을 제거한 형태이다. 그러므로 \( U \)도 \( m \times m \)에서 \( m \times n \)으로 크키가 줄어든다.

■ 위의 그림처럼, 왼쪽 특이벡터 행렬 \( U \)와 \( \Sigma \)의 크기를 줄여도 원래 행렬 \( A \)를 복구할 수 있다.
2.1.2 Compact SVD
■ compact SVD는 \( \Sigma \) 행렬에서 비대각 원소들과 대각 원소(특이값) 중 값이 0인 부분도 모두 제거한 형태이다.
■ 그리고 이에 대응하는 \( U \)와 \( V \)의 성분 또한 제거한다.
■ 즉, \( m \times n \) 크기의 대각행렬 \( \Sigma \)의 대각 원소를 \( \simga_1 \)부터 \( \simga_r \)까지로만 구성한다.
■ 그러므로 \( \Sigma \)의 크기는 \( r \times r \)로 줄어든다. 그래서 \( U \)의 크기는 \( m \times r \), \( V \)의 크기는 \( r \times r \)로 줄어든다.

■ 위의 그림처럼, \( U, \; \Sigma, \; V^T \)의 크기를 모두 줄여 원래 행렬 \( A \)를 복구할 수 있다.
2.1.3 Truncated SVD
■ truncated SVD는 대각행렬 \( \Sigma \)의 대각 원소(특이값) 중 상위 \( t \)개의 특이값만 선택한 형태이다. \( t < r \)
■ 이렇게 하면 \( m \times n \) 크기의 대각행렬 \( \Sigma \)의 크기는 \( t \times t \)로 줄어들고, 이에 대응하는 특이벡터 행렬 \( U \)와 \( V^T \)의 크기도 \( m \times t \), \( t \times t \)로 줄어들기 때문에 thin SVD와 compact SVD처럼 원래 행렬 \( A \)로 복구할 수 없다.
■ 상위 \( t \)개의 특이값을 선택해서 행렬을 재구성하기 때문에 행렬 \( A \)를 완전히 복구하지는 못하지만, 원래 행렬 \( A \)의 주요 특성은 유지하면서도 데이터 크기를 크게 줄일 수 있기 때문에 full SVD애 비해 계산 비용이 낮아진다.



■ 그리고 중요하지 않은 정보를 삭제하므로 데이터 압축, 이미지 노이즈 제거 등에서 근사 도구로 활용된다.
■ LSA도 truncated SVD를 사용한다. 설명력이 낮은 정보를 제거하고 설명력이 높은 정보를 남기기 위해서이다. 그리고 \( t \)는 LSA에서 찾고자하는 토픽의 수를 반영한 하이퍼파라미터값이다.
cf) \( \Sigma \) 행렬의 크기
- 행렬의 특이값 분해는 \( m \times n \) 크기의 비정방 행렬뿐만 아니라 정방행렬에도 적용할 수 있다.
- 예를 들어, \( 3 \times 3 \) 크기의 정방행렬을 분해했을 때, 대각 원소가 특이값인 대각 행렬 \( \Sigma \)은 \( \Sigma = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \)
으로 \( 3 \times 3 \)이 된다.
- \( m \times n \) 비정방 행렬인 경우에는 \( m > n \)인 경우와 \( m < n \)인 경우. 두 가지 경우로 나눌 수 있다.
- \( m > n \)
- 예를 들어, \( 4 \times 3 \)행렬인 경우에는 \( \Sigma = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \\ 0 & 0 & 0 \end{bmatrix} \)
- \( m < n \)
- 예를 들어, \( 3 \times 4 \)행렬인 경우에는 \( \Sigma = \begin{bmatrix} \sigma_1 & 0 & 0 & 0 \\ 0 & \sigma_2 & 0 & 0 \\ 0 & 0 & \sigma_3 & 0 \end{bmatrix} \)
2.2 잠재 의미 분석(LSA)
■ DTM이나 TF-IDF는 단어의 의미를 고려하지 못한다는 단점이 있다고 하였다.
■ LSA는 이러한 DTM이나 TF-IDF 행렬에 truncated SVD를 사용하여, 행렬의 차원(데이터의 차원)을 축소시켜 계산 효율성을 높이면서, 잠재적인(숨어있는) 의미를 이끌어낸다는 아이디어를 가지고 있다.
■ 예를 들어 다음과 같은 DTM이 있다고 할 때, 이 행렬에 (full) SVD를 수행하면

import numpy as np
np.set_printoptions(precision=2, suppress=True)
A = np.array(
[[1, 1, 1, 1, 0, 0],
[0, 3, 0, 1, 1, 0],
[0, 1, 1, 0, 1, 0],
[0, 2, 0, 1, 0, 1],
[2, 0, 1, 0, 0, 1],
[4, 0, 0, 3, 0, 1],
[0, 1, 2, 0, 5, 0],
[0, 3, 1, 0, 2, 1],
[0 ,2 ,1, 0, 2, 1],
[1, 0, 0, 2, 1, 0]]
)
print(f'DTM 크기: {np.shape(A)}')
```#결과#```
DTM 크기: (10, 6)
````````````## (full) SVD
U, s, VT = np.linalg.svd(A, full_matrices = True)
print(f'특이값 개수(대각 원소의 개수): {len(s)}개')
print(s);print()
```#결과#```
특이값 개수(대각 원소의 개수): 6개
[7.81 5.84 3.81 2.29 1.21 0.74]
````````````- 넘파이의 linalg.svd()는 특이값 분해의 결과로 대각 행렬 \( \Sigma \)의 대각 원소인 특이값의 리스트를 반환한다.
- 그러므로 \( \Sigma \) 행렬로 만들기 위해선 여기서 구한 특이값들을 대각 원소로 갖는 \( \Sigma \) 행렬을 다음과 같이 만들어야 한다.
## 대각 행렬
S = np.zeros((10, 6))
S[:6, :6] = np.diag(s)- 여기서 얻은 특이벡터 행렬 \( U \)와 \( V \)의 전치행렬은 직교행렬이므로 \( U^T U = I, \; V^T V = I \)가 성립한다.
print(f'원래 행렬 A의 크기: {np.shape(A)}')
print(A)
print(); print('(full) SVD 결과')
print(f'U의 크기: {np.shape(U)}')
print(U);print()
print(f'S의 크기: {np.shape(S)}')
print(S);print()
print(f'V^T의 크기: {np.shape(VT)}')
print(VT);print()
```#결과#```
원래 행렬 A의 크기: (10, 6)
[[1 1 1 1 0 0]
[0 3 0 1 1 0]
[0 1 1 0 1 0]
[0 2 0 1 0 1]
[2 0 1 0 0 1]
[4 0 0 3 0 1]
[0 1 2 0 5 0]
[0 3 1 0 2 1]
[0 2 1 0 2 1]
[1 0 0 2 1 0]]
(full) SVD 결과
U의 크기: (10, 10)
[[-0.16 0.2 0.1 0.09 0.75 0.31 0.28 0.24 0.26 -0.21]
[-0.33 0.01 0.48 -0.33 0.22 -0.57 0.2 -0.36 -0.03 0.09]
[-0.2 -0.07 -0. 0.1 0.41 0.14 -0.78 -0.26 -0.22 0.17]
[-0.19 0.1 0.46 -0.04 -0.28 0.56 0.12 -0.22 -0.42 -0.33]
[-0.1 0.27 -0.14 0.69 0.03 -0.07 0.35 -0.29 -0.26 0.37]
[-0.18 0.83 -0.13 -0.04 -0.17 -0.23 -0.27 0.07 0.07 -0.3 ]
[-0.6 -0.27 -0.63 -0.15 -0. -0.03 0.17 -0.07 -0.19 -0.29]
[-0.46 -0.12 0.29 0.23 -0.16 -0.13 -0.11 0.72 -0.15 0.2 ]
[-0.39 -0.11 0.09 0.21 -0.29 0.19 -0.09 -0.28 0.76 0.07]
[-0.16 0.28 -0.15 -0.52 -0.05 0.36 0.12 0.06 -0.01 0.67]]
S의 크기: (10, 6)
[[7.81 0. 0. 0. 0. 0. ]
[0. 5.84 0. 0. 0. 0. ]
[0. 0. 3.81 0. 0. 0. ]
[0. 0. 0. 2.29 0. 0. ]
[0. 0. 0. 0. 1.21 0. ]
[0. 0. 0. 0. 0. 0.74]
[0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 0. ]]
V^T의 크기: (6, 6)
[[-0.16 -0.58 -0.32 -0.2 -0.69 -0.17]
[ 0.74 -0.09 -0.06 0.57 -0.28 0.17]
[-0.23 0.76 -0.24 0.09 -0.53 0.15]
[ 0.34 0.05 0.45 -0.64 -0.26 0.46]
[ 0.07 0.15 0.61 0.07 -0.28 -0.72]
[-0.5 -0.24 0.51 0.46 -0.16 0.44]]
````````````■ 위의 결과는 일반적인 (full) SVD를 수행한 결과이다. 이제 \( t \)를 정하고, truncated SVD를 수행해보자.
- \( t = 3 \)으로 지정하였다.
## Truncated SVD
## t = 3
S = S[:3,:3] # 1행부터 3행까지 & 1열부터 3열까지
U = U[:,:3] # 전체 행 & 1열부터 3열까지
VT = VT[:3,:] # 1행부터 3열까지 & 모든 열
■ 축소된 행렬 \( U, S, V^T \)에 대해 다시 행렬 곱 연산을 하면, 다음과 같이 기존의 \( A \)와는 다른 행렬을 재구성한다.
A_prime = np.dot(np.dot(U, S), VT) # U @ S @ VT로 계산해도 된다.
print(f'A_prime의 크기: {np.shape(A_prime)}')
print(A_prime)
```#결과#```
A_prime의 크기: (10, 6)
[[ 0.98 0.91 0.24 0.95 0.34 0.46]
[ 0.02 2.89 0.4 0.7 0.81 0.72]
[-0.06 0.94 0.54 0.07 1.21 0.19]
[ 0.26 2.16 0.03 0.78 -0.05 0.61]
[ 1.44 -0.09 0.29 1.03 0.41 0.32]
[ 3.97 -0. 0.26 3.03 -0.11 0.97]
[ 0.1 1.01 2.17 -0.2 4.91 0.17]
[-0.21 2.98 0.93 0.4 2.07 0.66]
[-0.07 2.07 0.92 0.27 2.05 0.46]
[ 1.54 0.13 0.44 1.12 0.72 0.39]]
````````````
print(A)
```#결과#```
[[1 1 1 1 0 0]
[0 3 0 1 1 0]
[0 1 1 0 1 0]
[0 2 0 1 0 1]
[2 0 1 0 0 1]
[4 0 0 3 0 1]
[0 1 2 0 5 0]
[0 3 1 0 2 1]
[0 2 1 0 2 1]
[1 0 0 2 1 0]]
````````````
print(A - A_prime)
```#결과#```
[[ 0.02 0.09 0.76 0.05 -0.34 -0.46]
[-0.02 0.11 -0.4 0.3 0.19 -0.72]
[ 0.06 0.06 0.46 -0.07 -0.21 -0.19]
[-0.26 -0.16 -0.03 0.22 0.05 0.39]
[ 0.56 0.09 0.71 -1.03 -0.41 0.68]
[ 0.03 0. -0.26 -0.03 0.11 0.03]
[-0.1 -0.01 -0.17 0.2 0.09 -0.17]
[ 0.21 0.02 0.07 -0.4 -0.07 0.34]
[ 0.07 -0.07 0.08 -0.27 -0.05 0.54]
[-0.54 -0.13 -0.44 0.88 0.28 -0.39]]
````````````- 대체적으로 기존 행렬 \( A \)에서 0인 값들은 \( A' \)에서도 0에 가까운 값이 나오고, 1이었던 값들은 1에 가까운 값으로 나오는 것을 볼 수 있다.
- 그리고 값이 손실되었기 때문에 제대로 복원되지 않은 구간도 존재하는 것을 볼 수 있다.
■ 축소된 \( U \)의 크기를 보면 다음과 같이 \( 10 \times 3 \)의 크기를 가지는 것을 볼 수 있다. 이는 "문서(문장)의 개수 x t(토픽의 수)"이다.
print(f'U의 크기: {np.shape(U)}')
print(U)
```#결과#```
U의 크기: (10, 3)
[[-0.16 0.2 0.1 ]
[-0.33 0.01 0.48]
[-0.2 -0.07 -0. ]
[-0.19 0.1 0.46]
[-0.1 0.27 -0.14]
[-0.18 0.83 -0.13]
[-0.6 -0.27 -0.63]
[-0.46 -0.12 0.29]
[-0.39 -0.11 0.09]
[-0.16 0.28 -0.15]]
````````````즉, 축소된 행렬 \( U \)는 10개의 문서 각각을 3개의 토픽 값으로 표현하고 있다. 즉, U의 각 행은 잠재 의미를 표현하기 위한 수치화된 각각의 문서 벡터라고 볼 수 있다.
■ 축소된 행렬 \( V^T \)의 크기를 보면 3 x 6의 크기를 가지는 것을 볼 수 있다. 이는 "t(토픽의 수) x 단어의 개수"의 크기이다.
print(f'V^T의 크기: {np.shape(VT)}')
print(VT)
```#결과#```
V^T의 크기: (3, 6)
[[-0.16 -0.58 -0.32 -0.2 -0.69 -0.17]
[ 0.74 -0.09 -0.06 0.57 -0.28 0.17]
[-0.23 0.76 -0.24 0.09 -0.53 0.15]]
````````````즉, 축소된 \( V^T \)의 각 열은 잠재 의미를 표현하기 위해 수치화된 각각의 단어 벡터라고 할 수 있다.
■ 정리하면, '축소된 U의 각 행'은 '잠재 의미'를 표현하기 위한 수치화된 각각의 문서 벡터, '축소된 V^T의 각 열'은 '잠재 의미'를 표현하기 위해 수치화된 각각의 단어 벡터이다.
■ 그렇다면 이 축소된 행렬 \( U \)와 \( V \)가 각각 가지고 잇는 '잠재 의미'를 표현하기 위해서는 어떻게 해야 할까.
■ 원래 행렬에 대한 분산 또는 정보량를 가지고 있는 상위 \( t \)개의 특이값을 대각 원소로 가지고 잇는 축소된 \( \Sigma \)행렬을 각각 \( U \)와 \( V \)에 곱해줘서 잠재 의미를 표현할 수 있을 것이다.
■ 축소된 행렬 \( U \)와 \( S \)의 곱을 통해 잠재 의미를 표현하기 위한 수치화된 문서 행렬과 잠재 의미를 결합하여, 축소된 행렬 \( S \)와 \( V^T \)의 곱을 통해 잠재 의미를 표현하기 위한 단어 행렬과 잠재 의미를 결합하여 원래 DTM인 행렬 \( A \)에서 표현하던 단어들의 잠재적인 의미를 이끌어낼 수 있다.
■ 이 예에서 축소된 행렬 \( U \)와 \( S \)의 행렬곱 결과는 다음과 같다.
print(np.dot(U, S).shape)
print(U @ S)
```#결과#```
(10, 3)
[[-1.25 1.17 0.38]
[-2.61 0.04 1.83]
[-1.58 -0.43 -0.01]
[-1.52 0.57 1.75]
[-0.81 1.59 -0.55]
[-1.4 4.87 -0.51]
[-4.65 -1.59 -2.39]
[-3.59 -0.71 1.12]
[-3.02 -0.62 0.36]
[-1.24 1.62 -0.59]]
````````````- 행렬 \( US \)는 \( (10 \times 3) \times (3 \times 3) = 10 \times 3 \)크기의 행렬로, 각 행이 문서 벡터로 구성된 \( U \)에 각 토픽의 중요도가 저장되어 있는 \( \Sigma \)를 가중치로 반영한 가중합 결과로 볼 수 있다.

-- 정확히는 \( US \)의 각 행이 가중합 결과
- 즉, \( US \)는 토픽의 중요도(특이값)가 가중치로 적용된 문서-토픽 행렬이라고 할 수 있다.
- \( U \)의 각 값에 해당 토픽의 중요도(특이값)를 곱함으로써, 더 중요한 토픽에 더 높은 가중치를 부여하는 것으로 볼 수 있다.
- 예를 들어, 첫 번째 문서(dco1)의 경우 \( U \)와 \( S \)의 행렬곱으로 인해 [-0.16 x 7.81, 0.2 x 5.84, 0.1 x 3.81] = [-1.25, 1.17, 0.38]로 변환된다.
- 이러한 연산 과정을 보면, 문서가 각 잠재 토픽에 얼마나 관련되어 있는지, 토픽별 중요도를 고려한 표현이라고 볼 수 있다.
■ 이 예에서 축소된 행렬 \( S \)와 \( V^T \)의 행렬곱 결과는 다음과 같다.
print(np.dot(S, VT).shape)
print(S @ VT)
```#결과#```
(3, 6)
[[-1.24 -4.5 -2.5 -1.54 -5.37 -1.32]
[ 4.35 -0.51 -0.37 3.36 -1.61 0.97]
[-0.87 2.89 -0.91 0.33 -2.04 0.57]]
````````````- 행렬 \( SV^T \)는 \( (3 \times 3) \times (3 \times 6) = 3 \times 6 \)크기의 행렬로, 각 열이 단어 벡터로 구성된 \( V^T \)에 각 토픽의 중요도가 저장되어 있는 \( \Sigma \)를 가중치로 반영한 가중합 결과로 볼 수 있다.

-- 정확히는 \( SV^T \)의 각 열이 가중합 결과
- 즉, \( SV^T \)는 토픽의 중요도가 가중치로 적용된 토픽-단어 행렬이라고 할 수 있다.
- \( V^T \)의 각 값에 해당 토픽의 중요도(특이값)를 곱함으로써, 더 중요한 토픽에 더 높은 가중치를 부여하는 것으로 볼 수 있다.
- 연산 과정을 보면, \( V^T \)의 열인 '각 단어별 잠재된 의미(잠재 토픽)'가 \( \Sigma \)의 행과 곱해지는 것을 볼 수 있다.
- 예를 들어 \( V^T \)의 1열을 단어1, 1행을 잠재 토픽1, 2행을 잠재 토픽2, 3행을 잠재 토픽3이라고 했을 때,
- \( S \)의 1행과 \( V^T \)의 1열의 곱은 토픽의 중요도인 특이값이 가중치로 작동하여 [7.81 x -0.16, 0 x 0.74, 0 x -0.23] = [-1.24]로 변환된다.
- 이러한 과정을 \( V^T \)의 1열 전체에 적용했을 때 \( SV^T \)의 1열은 \( \begin{bmatrix} -1.24 \\ 4.35 \\ -0.87 \end{bmatrix} \)로 변환된 것을 확인할 수 있는데, 이는
- 해당 단어(첫 번째 단어)에서의 토픽별 중요도가 강조되는 것으로 볼 수 있다. 다시 말해, 토픽별 중요도를 고려한 단어의 표현이다.
■ \( US \)를 잠재 토픽 중요도가 반영된 문서 표현 행렬, \( SV^T \)를 잠재 토픽 중요도가 반영된 단어 표현 행렬이라고 해석이 가능한 이유는 truncated SVD를 통해 상위 \( t \)개의 특이값, 즉, 상위 \( t \)개의 잠재 토픽의 중요도를 선택했기 때문이다.
■ 이 예시에서는 데이터가 작으므로 차원축소의 효과가 드라마틱하게 보이지 않는다. 상위 \( t \)개의 특이값만 선택하기 때문에 데이터가 클 경우 차원축소의 효과가 도드라져 보일 것이다.
■ LSA는 이렇게 간단하게 단어의 잠재적인 의미(잠재 토픽)를 이끌어 낼 수 있어 문서의 유사도를 계산할 때 좋은 성능을 보일 수 있다. 하지만, 새로운 정보(문서 또는 단어)가 추가되면 처음부터 SVD를 다시 계산해야 한다. 그래서 LSA 대신, Word2Vec이나 워드 임베딩같은 단어의 의미를 벡터화하는 이런 경우에는 더 효율적이다.
'선형대수' 카테고리의 다른 글
| Singular value decomposition (2) - 특이값 분해 응용 (2) (0) | 2025.03.23 |
|---|---|
| Linear transformations and their matrices (0) | 2025.03.21 |
| Singular value decomposition (1) (0) | 2025.03.10 |
| Similar matrices and Jordan form (0) | 2025.03.07 |
| Positive definite matrices and minima (0) | 2025.03.05 |


