필터와 블러링

1. 컨볼루션(Convolution) 과 필터(Filter)

■ 영상 처리에서 인접 픽셀 값들을 참조하여 새로운 픽셀 값을 얻는 것을 공간 필터링(spacial filtering)이라 한다.
■ 이 필터링은 컨볼루션 연산을 이용해 커널(필터)을 영상 전체에 적용함으로써 이루어진다.

■ 다음 그림은 3 x 3 필터를 사용한 컨볼루션 연산 예시이다.

[출처] https://www.slipp.net/wiki/pages/viewpage.action?pageId=26641520

■ OpenCV에서 cv2.filter2D(src, ddepth, kernel, dst, anchor, delta, borderType) 함수로 컨볼루션 연산을 수행할 수 있다.
- src는 입력 영상/이미지 (배열)
- ddepth는 결과 이미지의 깊이(비트 단위: 8, 16, 32 등), -1로 지정하면 입력과 동일한 깊이 사용
- kernel은 커널(필터), n x n 크기의 배열(float32)
- dst는 출력 결과
- anchor는 커널 행렬에서 중싱점 위치, 디폴트 값은 (-1, -1) == 커널 중심
- delta는 컨볼루션 후 모든 픽셀에 추가할 값
- borderType는 가장자리 픽셀 처리 방법. 커널이 영상/이미지 가장자리에 적용될 때, 이미지 밖의 픽셀 값들을 어떻게 확장할지.

borderType	의미
BORDER_CONSTANT	이미지 가장자리 밖의 값을 모두 사용자가 지정한 상숫값으로 채움
BORDER_REPLICATE	이미지 가장자리를 반복하여 이미지 밖의 값을 채움.
BORDER_REFLECT	이미지 가장자리를 거울 반사처럼 처리. 경계의 첫 픽셀을 포함 ex) [123456]을 [21\|123456\|54]
BORDER_WRAP	이미지 반대쪽 가장자리의 값으로 이미지 가장자리 밖의 값을 채움.
BORDER_REFLECT_101	경계의 첫 픽셀을 포함하지 않음. ex) [123456]을 [2\|123456\|5]
BORDER_ISOLATED	이미지의 나머지 부분(가장자리 밖)을 고려하지 않음. 관심 영역(ROI)을 처리할 때 유용

2. 블러링(Blurring)

■ 블러링은 커널(필터)을 이용해서 마치 초점이 맞지 않은 사진처럼 영상을 흐릿하게(부드럽게) 만드는 필터링 기법으로 노이즈 제거에 효과적이다.

[출처] https://setosa.io/ev/image-kernels/

■ 대표적인 블러링 방법으로 평균 블러링, 가우시안 블러링, 미디언 블러링이 있다.

2.1 평균 블러링(Average Blurring)

■ 평균 블러링은 주변 픽셀 값들의 평균을 적용하는 가장 간단한 블러링 방법이다.

■ 주변 픽셀들의 평균값을 적용하기 때문에 픽셀 간 차이가 적어져 전체적으로 선명도가 떨어진다.(흐릿해진다.)

img = cv2.imread('img1.jpg')
kernel = np.ones((5,5))/5**2 # 크기가 5 x 5 이므로 채널 크기 5^2로 정규화 # 3 x 3이면 3^2으로 정규화...
kernel
```#결과#```
array([[0.04, 0.04, 0.04, 0.04, 0.04],
       [0.04, 0.04, 0.04, 0.04, 0.04],
       [0.04, 0.04, 0.04, 0.04, 0.04],
       [0.04, 0.04, 0.04, 0.04, 0.04],
       [0.04, 0.04, 0.04, 0.04, 0.04]])
````````````

average_blurring = cv2.filter2D(img, -1, kernel) # 평균 블러링 적용

cv2.imshow('original', img)
cv2.imshow('average_blurring', average_blurring)

cv2.waitKey()
cv2.destroyAllWindows()

■ OpenCV의 cv2.blur(src, ksize, dst, anchor, borderType) 함수를 이용하면 위의 예시처럼 직접 커널을 생성하지 않고도 커널 크기만 지정해 주면 평균 블러링을 적용할 수 있다.

- src는 입력 영상/이미지 (배열)

- ksize는 커널 크기. 커널 크기는 일반적으로 홀수로 지정.

- 나머지 파라미터는 cv2.filter2D( )와 동일

img = cv2.imread('img2.jpg')
blur1 = cv2.blur(img, (5, 5))
blur2 = cv2.blur(img, (9, 9))

merged = np.vstack((img, blur1, blur2))
cv2.imshow('blur', merged)
cv2.waitKey()
cv2.destroyAllWindows()

■ 필터(커널)의 크기가 커질수록 평균 블러링을 적용했을 때 전체적으로 선명도가 떨어지는(흐릿해지는) 것을 볼 수 있다.

■ 이는 필터의 크기가 커질수록 한 픽셀을 결정할 때 고려하는 주변 픽셀 범위가 넓어지기 때문이다.

■ 즉, 더 많은 주변 픽셀 값들을 평균 내므로 원래 픽셀 값의 특징이 희석되어 엣지(윤곽선, 경계선)같은 고주파 성분이 감소하며 결과적으로 선명도가 떨어진다.

cf) 같은 색상들이 모여 있는 부분은 저주파

■ cv2.blur( ) 함수와 동일한 기능을 하는 함수로 cv2.boxFilter(src, ddepth, ksize, dst, anchor, normalize, borderType) 함수가 있다. normalize = True로 지정하면 cv2.blur() 함수와 동일한 기능을 수행한다.

- src는 입력 영상/이미지 (배열)

- ddepth는 결과 이미지의 깊이(비트 단위: 8, 16, 32 등), -1로 지정하면 입력과 동일한 깊이 사용

- ksize는 커널 크기. 커널 크기는 일반적으로 홀수로 지정.

- normalize는 커널 크기로 정규화 지정 여부 $(1 / \text{ksize}^2)$ . 디폴트 값은 True

- 나머지 파라미터는 cv2.filter2D( )와 동일

blur3 = cv2.boxFilter(img, -1, (9,9))

np.array_equal(blur2, blur3)
```#결과#```
True
````````````

2.2 가우시안 블러링(Gaussian Blurring)

■ 가우시안 분포(또는 정규 분포(normal distribution)는 2개의 매개 변수 ① 평균 $( \mu)$ 와 표준편차에 의해 모양이 결정되고, 이때의 분포를 $N(\mu, \sigma^2)$ 로 표기한다.

■ 분포 형태는 다음 그림과 같이 평균 근처에 데이터의 개수가 많고, 평균에서 멀어질수록 개수가 적어진다.

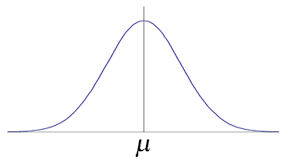
[출처] https://velog.io/@yunyoseob/Gaussian-Distribution-%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%AC

■ 이 가우시안 분포를 갖는 커널로 블러링하는 것을 가우시안 블러링이라고 한다.

■ 예를 들어 다음과 같은 커널(필터)가 가우시안 블러링 커널이다.

- 커널의 모든 원소의 합이 16이기 때문에 16으로 나눠준다.

■ 가우시안 블러링 커널을 중앙에 있는 가중치 값이 가장 크고 중앙에서 멀어질수록 가중치 값이 작아지기 때문에 가우시안 블러링 커널을 적용하면, 중심 픽셀 주변에 가까운 값은 더 크게 반영되고, 멀어질수록 적게 반영된다.

■ 이를 통해 노이즈 제거를 하면서 원본 형태와 명암 구조가 좀 더 유지되는 효과를 얻을 수 있다.

■ 예를 들어 대상 픽셀의 주변 픽셀 값들이 다음과 같을 때, 3 x 3 평균 블러링 커널을 적용해 보자. 평균 블러링 커널은 모든 요소가 동일한 가중치를 갖는다.

- 결과적으로 대상 픽셀(100)은 주변 픽셀 값들(대상 픽셀보다 낮거나 높은 픽셀)의 영향이 동일하게 반영되어 원래 값에서 다소 벗어난 새로운 값이 산출된다.

■ 이번에는 다음과 같은 가우시안 블러링 커널이 있다고 할 때, 해당 커널을 적용하면

- 산출된 값은 평균 블러보다 크게 다르지 않아 보일 수 있지만, 중요한 점은 중심 픽셀 주변에 가까운 값(대상 픽셀 100과 인접한 픽셀들)이 더 크게 반영되고, 멀어질수록 적게 반영되는 것을 볼 수 있다.

■ OpenCV에서 cv2.GaussianBlur(src, ksize, sigmaX, sigmaY, borderType) 함수나 cv2.getGaussianKernel(ksize, sigma, ktype) 함수를 이용해 가우시안 블러링을 적용할 수 있다.
■ cv2.GaussianBlur(src, ksize, sigmaX, sigmaY, borderType)
- src는 입력 영상/이미지 (배열)
- kernel은 커널(필터)
- sigmaX은 X 방향 표준편차로 0을 지정하면 자동으로 표준편차를 선택한다.
- sigmaY는 Y 방향 표준편차로 디폴트 값은 sigmaX이다.
- borderType에는 가장자리 픽셀 보정 방법을 지정한다.
■ cv2.getGaussianKernel(ksize, sigma, ktype)을 사용하는 방법은 cv2.getGaussianKernel( ) 함수에 커널 크기와 표준편차를 지정하면 1차원 가우시안 필터가 반환된다. 반환된 가우시안 필터를 cv2.filter2D( ) 함수의 kernel 파라미터에 지정하면 된다.

img = cv2.imread('img2.jpg')

k1 = cv2.getGaussianKernel(3, 0)
k1 # 반환된 가우시안 필터는 1차원이므로
```#결과#```
array([[0.25],
       [0.5 ],
       [0.25]])
````````````

k1*k1.T # 2차원 행렬로 만들어 준다.
```#결과#```
array([[0.0625, 0.125 , 0.0625],
       [0.125 , 0.25  , 0.125 ],
       [0.0625, 0.125 , 0.0625]])
````````````

blur1 = cv2.filter2D(img, -1, k1*k1.T)
blur2 = cv2.GaussianBlur(img, (5, 5), 0)

merged = np.vstack( (img, blur1, blur2))
cv2.imshow('blur', merged)
cv2.waitKey( )
cv2.destroyAllWindows()

2.3 미디언 블러링(Median Blurring)

■ 커널(필터)의 (정렬된) 픽셀 값에서 중앙값(median)에 해당되는 픽셀 값으로 대상 픽셀 값을 대체하는 방법이다.

■ OpenCV에서 cv2.medianBlur(src, ksize) 함수로 미디언 블러링을 적용할 수 있다.
- src: 입력 영상/이미지
- ksize: 커널(필터) 크기

■ 이 방법은 소금&후추 잡음(salt&pepper noise)을 제거에 효과적이다. 소금&후추 잡음이란 잡음이 마치 소금과 후추처럼 흰색(255) 또는 검은색(0)으로 이뤄진 잡음을 말한다. 즉, 영상/이미지의 임의의 픽셀을 0 또는 255로 만드는 잡음이다.

import random

## 소금-후추 잡음 생성 함수
def salt_and_pepper_noise(image, amount=0.09):
    noisy_image = image.copy()
    num_pixels = int(amount * image.size) # 소금-후추 잡음 추가할 픽셀의 총 개수
    
    # 소금 잡음
    for _ in range(num_pixels // 2): # 반은 소금
        i = random.randint(0, image.shape[0] - 1)
        j = random.randint(0, image.shape[1] - 1)
        noisy_image[i, j] = [255, 255, 255]  # 흰색 (소금)
    
    # 후추 잡음
    for _ in range(num_pixels // 2): # 반은 후추
        i = random.randint(0, image.shape[0] - 1)
        j = random.randint(0, image.shape[1] - 1)
        noisy_image[i, j] = [0, 0, 0]  # 검은색 (후추)
    
    return noisy_image

img = cv2.imread('000.jpg') # (원본) 입력 이미지
noisy_img = salt_and_pepper_noise(img, amount=0.02) # 소금-후추 잡음이 포함된 이미지
blur = cv2.medianBlur(noisy_img, 3) # 미디언 블러링 적용

plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('original'),plt.xticks([]); plt.yticks([])
plt.subplot(132),plt.imshow(noisy_img[:,:,::-1]),plt.title('salt&pepper noise'),plt.xticks([]); plt.yticks([])
plt.subplot(133),plt.imshow(blur[:,:,::-1]),plt.title('median blurring'),plt.xticks([]); plt.yticks([])
plt.show()

2.4 바이레터럴 필터(Bilateral Filter)

■ 블러링만 적용하면(하나의 필터만 사용하면) 경계를 흐릿하게 만드는 문제가 있다. 이 문제점을 개선하기 위해 경계 필터를 하나 더 사용해서 보정을 수행한다.

■ 이를 통해 경계도 뚜렷하고 노이즈도 제거되는 효과가 있지만 필터를 2개 사용하기 때문에 연산량이 증가하므로 속도가 느려진다는 단점이 있다.

■ 바이레터럴 필터는 가우시안 필터와 경계 필터를 결합한 것으로 OpenCV서 cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace, dst, borderType) 함수를 통해 이용할 수 있다.

- src는 입력 영상/이미지
- d: 필터링 중에 사용되는 픽셀 주변의 직경(diameter), 5보다 크면 매우 느림. 양수가 아닌 경우 sigmaSpace에 비례
- sigmaColor: 색 공간의 시그마 값. 값이 클수록 더 멀리 있는 색상이 함께 혼합
- sigmaSpace: 좌표 공간의 시그마 값. 이 파라미터는 값이 클수록 주변 픽셀에 영향을 미침
- 보통 sigmaColor와 sigmaSpace는 동일한 값을 사용하며, 10에서 150 사이의 값이 권장된다.

img = cv2.imread('img2.jpg')
blur1 = cv2.GaussianBlur(img, (5,5), 0) # 가우시안 필터
blur2 = cv2.bilateralFilter(img, 5, 10, 10) # 바이레터럴 필터

merged = np.vstack((img, blur1, blur2))
cv2.imshow('blur', merged)
cv2.waitKey( )
cv2.destroyAllWindows()

- 가우시안 필터를 적용한 경우, 산 쪽으로 갈수록 경계선이 흐릿해지는 것을 볼 수 있다. 반면, 바이레터럴 필터를 적용한 경우 경계선이 유지되는 것을 볼 수 있다.

3. 경계(엣지) 검출

3.1 기본 미분 필터

■ 예를 들어 전체가 흰색 화면이라면 이 화면의 주파수는 저주파이다. 같은 색상들이 모여 있는 부분은 저주파를 나타내기 때문이다.

■ 만약, 이 (저주파인) 화면에서 하얀색이 아닌 다른 색이 지나간다면, 이 다른 색이 표현된 선은 경계선(엣지)이 되며, 고주파 성분을 갖게 되므로 하얀색에서 다른 색으로 접근할수록 주파수가 커지게 된다.
■ 그러므로 경계를 추출하기 위해선 픽셀 값이 급격하게 변하는 지점을 찾아야 한다. 급격하게 변하는 지점은 미분을 이용해 찾아낼 수 있다.

■ 하지만 픽셀은 이산 공간에 있으므로 연속 함수에서 쓰는 미분을 그대로 적용하기 어렵다. 그러므로 인접 픽셀 간의 차를 이용해 미분을 근사한다.

■ 디지털 이미지에서 $f(x, y)$ 는 $(x, y)$ 위치의 픽셀 값을 의미한다. 그러므로 $x$ 방향(가로 방향)으로 미분을 근사한다면 $\dfrac{\partial f}{\partial x} \approx f(x+1, y) - f(x, y)$ 으로 나타낼 수 있다.

- 여기서 $f(x + 1, y)$ 는 $(x + 1, y)$ 위치(오른쪽 픽셀), $f(x, y)$ 는 $(x, y)$ 위치(현재 픽셀)을 의미하며, 이 두 픽셀 값을 빼주면 오른쪽 픽셀에서 현재 픽셀을 뺀 값이 된다.

■ 이 연산을 커널로 표현하면 [ -1 1 ]이 된다.

- 현재 픽셀에 -1을 곱하고 오른쪽 픽셀에 +1을 곱한 뒤, 둘을 더하면 오른쪽 픽셀 - 현재 픽셀이 계산된다.

■ $y$ 방향(세로 방향)도 마찬가지이다. $\dfrac{\partial f}{\partial y} \approx f(x, y+1) - f(x, y)$ 이며, 커널로 표현하면 2행 1열의 [-1 1 ]이 된다.

- 현재 픽셀에 -1을 곱하고 아래 픽셀에 +1을 곱한 뒤, 둘을 더하면 아래 픽셀 - 현재 픽셀이 계산된다.

■ $x$ 방향, $y$ 방향에 대해 각각 기본 미분 커널([-1 1])을 적용하면, 수직/수평 경계가 두드러지는 엣지를 추출할 수 있다.

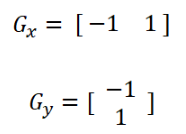
img = cv2.imread('img2.jpg')

## 미분 커널
gx_kernel = np.array([[ -1, 1]])
gy_kernel = np.array([[ -1],[ 1]])

print(gx_kernel); print(gy_kernel)
```#결과#```
[[-1  1]]
[[-1]
 [ 1]]
````````````

## 미분 커널 적용
edge_gx = cv2.filter2D(img, -1, gx_kernel)
edge_gy = cv2.filter2D(img, -1, gy_kernel)

merged = np.vstack((img, edge_gx, edge_gy))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

- 마지막은 상하/좌우 경계 필터로 추출한 필터링 결과를 합친 이미지이다.

■ 픽셀 값의 변화가 없는 부분은 미분 값이 0이므로 검은색으로 나타난다.

■ $x$ 방향 미분 필터는 왼쪽 픽셀과 오른쪽 픽셀의 값 차이를 계산하기 때문에 픽셀 값이 갑자기 바뀌는 지점은 수직 경계(세로선)에서 나타나며,

반대로 $y$ 방향 미분 필터는 위쪽 픽셀과 아래쪽 픽셀의 값 차이를 계산하기 때문에 픽셀 값이 갑자기 바뀌는 지점은 수평 경계(가로선)에서 나타난다.

■ 즉, $x$ 방향 미분 필터는 세로 방향의 경계, $y$ 방향 미분 필터는 가로 방향의 경계를 검출한다.

3.2 로버츠 교차 필터 (Roberts Cross Filter)

■ 로버츠 교차 필터는 다음과 같이 커널 대각선 방향에 +1과 -1을 배치시켜 사선(대각선) 경계에서 발생하는 밝기 변화에 민감하기 때문에 사선 경계 검출에 효과적이다.

■ 단, 2 x 2 크기의 작은 커널을 사용하기 때문에 노이즈의 영향을 많이 받는다. 작은 커널을 사용하면 원본 이미지에 존재하는 개별 픽셀의 노이즈가 필터링 결과에 큰 영향을 미치기 때문이다.

img = cv2.imread('img2.jpg')

# 로버츠 교차 커널
gx_kernel = np.array([[1,0], [0,-1]])
gy_kernel = np.array([[0, 1], [-1,0]])

print(gx_kernel);print();print(gy_kernel)
```#결과#```
[[ 1  0]
 [ 0 -1]]

[[ 0  1]
 [-1  0]]
````````````

# 로버츠 교차 커널 적용
edge_gx = cv2.filter2D(img, -1, gx_kernel)
edge_gy = cv2.filter2D(img, -1, gy_kernel)

merged = np.vstack((img, edge_gx, edge_gy, edge_gx + edge_gy))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

3.3 프리윗 필터 (Prewitt Filter)

■ 프리윗 필터는 중앙 차분을 사용하며 $x$ 축과 $y$ 축 각 방향으로 차분을 세 번 계산하기 때문에 기본 미분 필터나 로버츠 교차 필터에 비해 상하(수직)/좌우(수평) 경계를 검출하는 데 효과적이다.

- 가로 (-1, 0, +1)은 $x$ 방향(가로 방향)으로 미분을, 세로 (-1, 0, +1)은 $y$ 방향(세로 방향)으로 미분을 진행한다.

■ 하지만 대각선 검출에 있어서는 상대적으로 약한 성능을 보인다.

■ 예를 들어 다음과 같이 대각선 엣지가 있는 이미지를 고려해보자.

img = cv2.imread('Image2.png')
img.shape
```#결과#```
(10, 10, 3)
````````````

plt.imshow(img, cmap='gray')

■ 이 이미지에 프리윗 필터를 적용해 경계를 검출한 결과 상하/좌우 경계는 잘 검출하지만 대각선 검출은 약한 것을 확인할 수 있다.

## 프리윗 커널
gx_kernel = np.array([[-1,0,1], [-1,0,1],[-1,0,1]])
gy_kernel = np.array([[-1,-1,-1],[0,0,0], [1,1,1]])

# 프리윗 커널 적용
edge_gx = cv2.filter2D(img, -1, gx_kernel)
edge_gy = cv2.filter2D(img, -1, gy_kernel)

plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('original'),plt.axis('off')
plt.subplot(132),plt.imshow(edge_gx[:,:,::-1]),plt.title('edge_gx'),plt.axis('off')
plt.subplot(133),plt.imshow(edge_gy[:,:,::-1]),plt.title('edge_gy'),plt.axis('off')
plt.show()

■ 이러한 이유는 프리윗 필터를 단순히 -1, 0, 1만 사용하며 가중치가 균등하게 분포되어 있기 때문에 대각선 주변의 픽셀 값과 대각선의 픽셀 값이 같은 값(또는 비슷한 값)읕 가지게 되어 대각선 경계를 구별하는 것이 어렵다.

## 입력 이미지 Image의 배열과 edge_gx 배열 비교
img
```#결과#```
array([[[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 69,  69,  69]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 97,  97,  97],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 99,  99,  99],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [100, 100, 100],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [102, 102, 102],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [102, 102, 102],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[ 74,  74,  74],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]]], dtype=uint8)
````````````

edge_gx
```#결과#```
array([[[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [192, 192, 192],
        [ 69,  69,  69],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [ 96,  96,  96],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [ 96,  96,  96],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 97,  97,  97],
        [ 96,  96,  96],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 99,  99,  99],
        [ 97,  97,  97],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [100, 100, 100],
        [ 99,  99,  99],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [102, 102, 102],
        [100, 100, 100],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [102, 102, 102],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [ 28,  28,  28],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]]], dtype=uint8)
``````````

■ 즉, 프리윗 필터를 적용하면 저주파 영역이 되어 고주파 성분(엣지)를 검출하기 어렵다.

img = cv2.imread('img2.jpg')

## 프리윗 커널
gx_kernel = np.array([[-1,0,1], [-1,0,1],[-1,0,1]])
gy_kernel = np.array([[-1,-1,-1],[0,0,0], [1,1,1]])

# 프리윗 커널 적용
edge_gx = cv2.filter2D(img, -1, gx_kernel)
edge_gy = cv2.filter2D(img, -1, gy_kernel)

merged = np.vstack((img, edge_gx, edge_gy, edge_gx + edge_gy))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

- 대각선 경계 검출은 약하지만, 기본 미분 필터와 로버츠 교차 필터에 비해 상하/좌우 경계는 뚜렷하게 검출하는 것을 볼 수 있다.

3.4 소벨 필터 (Sobel Filter)

■ 소벨 필터는 중앙 차분을 사용하며, 프리윗 필터와 달리 다음과 같이 중심 픽셀의 차분 비중을 두 배로 적용한 필터이다.

■ 소벨 필터는 중앙 행(또는 열)에 프리윗 필터와 달리 2배의 가중치를 두어 엣지 근방에서의 변화량을 더 크게 반영한다.

■ 그러므로 대각선 방향에서 픽셀 값이 점진적으로 변할 때, 대각선 경계를 프리윗 필터보다 더 확실하게 잡아낼 수 있다.

gx_kernel = np.array([[-1,0,1], [-2,0,2],[-1,0,1]])
gy_kernel = np.array([[-1,-2,-1],[0,0,0], [1,2,1]])

print(gx_kernel);print();print(gy_kernel)
```#결과#```
[[-1  0  1]
 [-2  0  2]
 [-1  0  1]]

[[-1 -2 -1]
 [ 0  0  0]
 [ 1  2  1]]
````````````

edge_gx = cv2.filter2D(img, -1, gx_kernel)
edge_gy = cv2.filter2D(img, -1, gy_kernel)

edge_gx
```#결과#```
array([[[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [192, 192, 192],
        [138, 138, 138],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [192, 192, 192],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 96,  96,  96],
        [192, 192, 192],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 97,  97,  97],
        [192, 192, 192],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [ 99,  99,  99],
        [194, 194, 194],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [100, 100, 100],
        [198, 198, 198],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [102, 102, 102],
        [200, 200, 200],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [204, 204, 204],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [ 28,  28,  28],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]],

       [[  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0],
        [  0,   0,   0]]], dtype=uint8)
````````````

plt.subplot(131),plt.imshow(img[:,:,::-1]),plt.title('original'),plt.axis('off')
plt.subplot(132),plt.imshow(edge_gx[:,:,::-1]),plt.title('edge_gx'),plt.axis('off')
plt.subplot(133),plt.imshow(edge_gy[:,:,::-1]),plt.title('edge_gy'),plt.axis('off')
plt.show()

■ cv2.filter2D( ) 함수를 이용해 소벨 필터를 적용해도 되지만, OpenCV에서 별도의 소벨 필터 함수 cv2.Sobel(src, ddepth, dx, dy, dst, ksize, scale, delta, borderType)를 제공한다.

- src는 입력 영상/이미지

- ddepth는 출력 영상의 dtype. -1로 지정하면 입력과 동일

- dx, dy는 미분 차수로 0, 1, 2 중 선택할 수 있다. 0은 0차 미분, 1은 1차 미분, 2는 2차 미분을 의미하며, dx와 dy 둘 다 0일 수는 없다.

- ksize는 커널 크기

- scale은 연산 결과에 추가적으로 곱할 값

- delta는 연산 결과에 추가적으로 더할 값이다.

- borderType에는 가장자리 픽셀 보정 방법을 지정한다.

img = cv2.imread('img2.jpg')

## 소벨 필터 적용
sobel_gx = cv2.Sobel(img, -1, 1, 0, ksize=3)
sobel_gy = cv2.Sobel(img, -1, 0, 1, ksize=3)

merged = np.vstack((img, sobel_gx, sobel_gy, sobel_gx + sobel_gy))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

3.5 샤르 필터 (Scharr Filter)

■ 샤벨 필터의 단점은 커널 중심에서 멀어질수록 엣지 방향성의 정확도가 떨어진다. 이러한 이유는 커널 중심에서 멀어질수록 이미지의 엣지가 모호해지기 때문이다.

■ 샤벨 필터는 중심 픽셀에 더 높은 가중치를 부여하기 때문에 주변 픽셀은 상대적으로 낮은 가중치를 가지게 된다.

■ 그러므로 중심에 가까운 픽셀에서는 엣지 방향성을 비교적 정확하게 검출할 수 있지만, 중심에서 멀어질수록 낮은 가중치가 적용되어 이미지의 엣지가 모호해져 정확도가 떨어진다.

■ 샤르 필터는 샤벨 필터의 단점을 개선한 것으로 다음과 같이 샤벨 필터와 달리 주변 픽셀에도 보다 높은 가중치를 부여한다.

■ cv2.filter2D( ) 함수를 이용해 소벨 필터를 적용해도 되지만, OpenCV에서 별도의 샤르 필터 함수 cv2.Scharr(src, ddepth, dx, dy, dst, scale, delta, borderType)를 제공한다.

- 파라미터에 ksize가 없는 것을 제외하면 모든 파라미터는 cv2.Sobel()과 동일하다.

img = cv2.imread('img2.jpg')

## 샤르 필터 적용
scharr_gx = cv2.Scharr(img, -1, 1, 0)
scharr_gy = cv2.Scharr(img, -1, 0, 1)

merged = np.vstack((img, scharr_gx, scharr_gy, scharr_gx + scharr_gy))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

- 샤르 필터는 전체적으로 높은 가중치를 부여하기 때문에 샤벨 필터보다 엣지의 굵기가 더 굵게 검출되는 것을 확인할 수 있다.

3.6 라플라시안 필터 (Laplacian Filter)

■ 라플라시안 필터는 2차 미분을 적용해 픽셀 값의 변화율이 큰 지점을 감지할 수 있다. 정확히는 2차 미분을 통해 엣지의 변곡점을 찾기 때문에 경계를 더 정확하게 검출할 수 있는 필터이다.

■ OpenCV에서 cv2.Laplacian(src, ddepth, dst, ksize, scale, delta, borderType) 함수를 이용해 라플라시안 필터를 적용할 수 있다.

- 파라미터는 cv2.Sobel()과 동일하다.

img = cv2.imread('img2.jpg')

## 라플라시안 필터 적용
edge = cv2.Laplacian(img, -1)

merged = np.vstack((img, edge))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

3.7 캐니 엣지 (Canny Edge)

■ 캐니 엣지 검출은 그래디언트의 크기와 방향을 모두 고려하여 더 정확한 경계를 찾기 위한 방법으로, 다음 4단계 알고리즘을 거쳐 경계를 검출한다.

(1) 노이즈 제거 - 가우시안 필터링

- 가우시안 블러링 필터를 통해 노이즈를 제거한다.

(2) 경계 그래디언트 계산

- 소벨 필터를 사용해 노이즈가 제거된 이미지에서 픽셀의 그래디언트의 크기와 방향을 계산한다.

(3) 비최대 억제(Non-Maximum Suppression)

- 비최대 억제는 엣지의 정확한 위치를 파악하기 위해 사용되는 방법으로, 여러 개의 픽셀에 의해 하나의 엣지가 표현되는 현상을 방지한다.

- 이를 위해 그래디언트 방향을 따라 그래디언트 크기가 최대인 픽셀만 엣지 픽셀로 설정하고 나머지 모든 픽셀은 제거한다.

(4) 이중 임곗값을 이용한 히스테리시스 엣지 트래킹

- 캐니 엣지 검출은 두 개의 임곗값을 사용한다. 두 개의 임곗값 중에서 낮은 임곗값을 low, 높은 임곗값을 high라고 했을 때,

- high보다 큰 그래디언트 값을 갖는 픽셀은 항상 엣지의 픽셀로 판단하고 low보다 작은 그래디언트 값을 갖는 픽셀은 엣지 픽셀이 될 수 없는 픽셀로 판단한다.

- low보다 크고 high 사이에 있는 픽셀들은 히스테리시스 엣지 트래킹 방법을 사용하여 엣지의 픽셀로 사용할 수 있는지 판별한다.

- 히스테리시스 엣지 트래킹은 low보다 크고 high 사이에 있는 픽셀들 중 high보다 큰 그래디언트 값을 갖는 픽셀과 서로 연결되어 있는 픽셀만 엣지의 픽셀로 판단한다.

- 이는 다음 그림과 같이 엣지가 서로 연결되어 있는 가능성이 높다는 점을 고려한 것으로 그래디언트 크기가 다소 작게 나오는 엣지도 놓치지 않고 찾을 수 있다.

이중 임곗값을 이용한 히스토리 엣지 트래킹 (색칠된 부분이 최종 엣지의 픽셀) [출처] https://velog.io/@redorangeyellowy/ch06-%EC%98%81%EC%83%81%EC%9D%98-%ED%8A%B9%EC%A7%95-%EC%B6%94%EC%B6%9C-%EC%BA%90%EB%8B%88-%EC%97%90%EC%A7%80-%EA%B2%80%EC%B6%9C

- low보다 작은 픽셀들은 최종 엣지에 포함되지 않는 것을 위의 그림에서 확인할 수 있다.

■ OpenCV는 캐니 엣지 함수 cv2.Canny(img, threshold1, threshold2, edges, apertureSize, L2gardient)를 제공한다.

- img는 입력 영상/이미지

- threshold1, threshold2는 순서대로 하단 임곗값 low, 상단 임곗값 high이다.

- apertureSize는 소벨 마스크에 사용할 커널 크기

- L2gradient는 그레디언트 강도를 구할 방식으로 True로 지정하면 L2(제곱 합의 루트), False로 지정하면 L1(절댓값의 합)을 사용한다.

img = cv2.imread('img2.jpg')

## 케니 엣지 적용
edges = cv2.Canny(img,100,200)

merged = np.vstack((img, edge))
cv2.imshow('edge', merged)
cv2.waitKey()
cv2.destroyAllWindows()

'OpenCV' 카테고리의 다른 글

분할(segmentation) (1) (1)	2024.12.22
모폴로지(Morphology) 연산, 이미지 피라미드(Image Pyramid) (0)	2024.12.21
기하학적 변환 (2) (0)	2024.12.16
기하학적 변환 (1) (0)	2024.12.16
이미지 프로세싱 (3) (0)	2024.12.15

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Hyun_Jae

필터와 블러링

'OpenCV' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

필터와 블러링

'OpenCV' 카테고리의 다른 글

'OpenCV' Related Articles

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역