기하학적 변환 (1)

1. 이동(Translation)

■ 기존 좌표를 \( x_{\text{old}}, y_{\text{old}} \)라고 했을 때, 이미지를 이동하는 방법은 기존 좌표에 이동시키려는 거리 \( d_1, d_2 \)를 더해주면 된다. \[
\begin{cases}
x_{\text{new}} = x_{\text{old}} + d_1 \\
y_{\text{new}} = y_{\text{old}} + d_2
\end{cases}
\Leftrightarrow
\begin{cases}
x_{\text{new}} = 1x_{\text{old}} + 0y_{\text{old}} + d_1 \\
y_{\text{new}} = 0x_{\text{old}} + 1y_{\text{old}} + d_2
\end{cases}
\] ■ 이 방정식을 행렬식으로 표현하면 다음과 같다. \[
\begin{pmatrix}
1 & 0 & d_1 \\
0 & 1 & d_2
\end{pmatrix}
\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
d_1 + x \\
d_2 + y
\end{pmatrix}
\] 여기서 2 x 3 행렬 \(
\begin{pmatrix}
1 & 0 & d_1 \\
0 & 1 & d_2
\end{pmatrix}
\)이 이미지의 좌표를 이동시키는 변환 행렬이다. 이 변환 행렬에 좌표를 곱해주면 이동된 좌표가 계산된다.

■ 변환 행렬에서 (1, 0 , 0, 1) 부분이 확대/축소, 회전, 변형의 역할을 수행하고 \( d_1, d_2 \)은 각 축(\( x, y \))에 대한 이동을 수행한다. 여기서 단위 행렬 부분의 대각 원소가 1이므로 '이동'만 고려한 변환 행렬임을 알 수 있다.

■ OpenCV에서는 cv2.warpAffine(src, matrix, dsize, dst, flags, borderMode, borderValue) 함수로 변환 행렬을 이용해서 이미지를 변환할 수 있다.
- src는 원본 이미지 (배열)
- matrix에는 2 x 3 변환 행렬을 지정한다.
- dsize는 결과 이미지의 크기 (width, height)
- flags는 보간법 알고리즘 플래그로 다음과 같은 방법들을 선택할 수 있다.

flags	의미
cv2.INTER_LINEAR	인접한 4개 픽셀 값에 거리 가중치 사용 (디폴트 값)
cv2.INTER_NEAREST	가장 가까운 픽셀 값 사용
cv2.INTER_AREA	픽셀 영역 관계를 이용한 리샘플링 방법
cv2.INTER_CUBIC	인접한 16개 픽셀(= 4 x 4 픽셀) 값에 거리 가중치 사용

- borderMode는 가장자리 영역 보정 플래그로 다음과 같은 방법들을 선택할 수 있다.

borderMode	의미
cv2.BORDER_CONSTANT	고정 색상 값
cv2.BORDER_REPLICATE	가장자리 복제
cv2.BORDER_WRAP	반복
cv2.BORDER_REFLECT	반사

- borderValue는 가장자리 영역 보정 플래그로 cv2.BORDER_CONSTANT를 지정할 경우 사용할 가장자리 색상 값으로 디폴트 값은 0이다.

img = cv2.imread('opencv_logo.png')

## height를 행,  width를 열 또는 y, x 축으로 볼 수 있음
height, width = img.shape[0:2]  # 영상/이미지의 크기

## 이동할 거리
dx, dy = 10, 20 

## 변환 행렬
trans_matrix = np.float32([[1, 0, dx], [0, 1, dy]]) # 이동만 고려
trans_matrix 
```#결과#```
array([[ 1.,  0., 10.],
       [ 0.,  1., 20.]], dtype=float32)
````````````

## 단순 이동
dst = cv2.warpAffine(threshold_127, trans_matrix, (width, height))
dst2 = cv2.warpAffine(img, trans_matrix, (width+dx, height+dy))

## 지워진 가장자리 픽셀 영역 보정
dst3 = cv2.warpAffine(img, trans_matrix, (width+dx, height+dy), None, 
                      cv2.INTER_LINEAR, cv2.BORDER_CONSTANT, (255,0,0) ) # 파란색
                      
dst4 = cv2.warpAffine(img, trans_matrix, (width+dx, height+dy), None,
                      cv2.INTER_LINEAR, cv2.BORDER_REFLECT) # 원본 반사
                      
dst5 = cv2.warpAffine(img, trans_matrix, (width+dx, height+dy), None,
                      cv2.INTER_LINEAR, cv2.BORDER_WRAP) # 반복

titles = ['original', 'trans1', 'trans2', 'border_constant', 'border_reflect','border_replicate']
images = [img, dst, dst2, dst3, dst4, dst5]

for i in range(6):
    plt.subplot(2, 3, i+1)
    plt.imshow(images[i][:,:,::-1])
    plt.title(titles[i])
    plt.xticks([]); plt.yticks([])
plt.show()

- trans1을 제외한 이미지들은 원본 이미지를 오른쪽(x)으로 10픽셀, 아래(y)로 20픽셀 평행 이동시킨 결과이다.

- 평행 이동이 적용되면 기존 영역의 가장자리 부분이 잘리게 된다. 이때  borderMode 파라미터에 지정해 잘린 가장자리 픽셀 영역을 보정할 수 있다.

 

2. 확대/축소(Scaling)

■ 이미지를 일정 비율로 확대/축소하는 방법은 단위 행렬 부분의 대각 원소에 특정 값을 곱하면 된다. 이를 방정식과 행렬식으로 표현하면 다음과 같다. \[
\begin{cases}
x_{\text{new}} = a_1 \cdot x_{\text{old}} \\
y_{\text{new}} = a_2 \cdot y_{\text{old}}
\end{cases}
\Leftrightarrow
\begin{cases}
x_{\text{new}} = a_1 \cdot x_{\text{old}} + 0 \cdot y_{\text{old}} + 0 \cdot 1 \\
y_{\text{new}} = 0 \cdot x_{\text{old}} + a_2 \cdot y_{\text{old}} + 0 \cdot 1
\end{cases}
\Leftrightarrow
\begin{pmatrix}
a_1 & 0 & 0 \\
0 & a_2 & 0
\end{pmatrix}
\cdot
\begin{pmatrix}
x \\
y \\
1
\end{pmatrix}
=
\begin{pmatrix}
a_1 x \\
a_2 y
\end{pmatrix}
\] cf) cv2.warpAffine( ) 함수를 사용하기 위해 변환 행렬을 2 x 3 크기로 맞춰야 한다.

img = cv2.imread('opencv_logo.png')
height, width = img.shape[:2]

## 0.5배 (축소) 변환 행렬
shrink_05 =  np.float32([[0.5, 0, 0],
                         [0, 0.5,0]]) 

## 2배 (확대) 변환 행렬
zoom_2 = np.float32([[2, 0, 0],
                     [0, 2, 0]])

## 보간법 적용 없이 확대/축소
dst1 = cv2.warpAffine(img, shrink_05, (int(height*0.5), int(width*0.5)))
dst2 = cv2.warpAffine(img, zoom_2, (int(height*2), int(width*2)))

## 보간법 적용 확대/축소
dst3 = cv2.warpAffine(img, shrink_05, (int(height*0.5), int(width*0.5)), None, cv2.INTER_AREA)
dst4 = cv2.warpAffine(img, zoom_2, (int(height*2), int(width*2)), None, cv2.INTER_CUBIC)

img.shape, dst1.shape, dst2.shape, dst3.shape, dst4.shape
```#결과#```
((120, 98, 3), (49, 60, 3), (196, 240, 3), (49, 60, 3), (196, 240, 3))
````````````

- 일반적으로 축소에는 cv2.INTER_AREA를, 확대에는 cv2.INTER_CUBIC, cv2.INTER_LINEAR를 사용한다.

 

titles = ['original', 'dst1', 'dst2', 'dst3', 'dst4']
images = [img, dst, dst2, dst3, dst4, dst5]

for i in range(5):
    plt.subplot(2, 3, i+1)
    plt.imshow(images[i][:,:,::-1])
    plt.title(titles[i])
    plt.xticks([]); plt.yticks([])
plt.subplots_adjust(wspace=0.5)
plt.show()

■ cv2.resize(src, dsize, dst, fx, fy, interpolation) 함수를 사용하면 변환 행렬을 사용하지 않고도 확대/축소를 몇 픽셀로 할 것인지 또는 몇 배율을 적용할 것인지를 선택할 수 있다.
- src는 원본 이미지 (배열)
- dsize: 결과 이미지의 크기(확대/축소 목표 크기) (width, height)형식으로, 생략하면 fx, fy 배율을 적용한다.
- fx, fy: 크기 배율이다. 만약, dsize가 지정되면 dsize를 적용한다.
- interpolation: 보간법 알고리즘 선택 플래그로 cv2.warpAffine()과 동일하다.

img = cv2.imread('opencv_logo.png')
height, width = img.shape[:2]

## 크기(dsize) 지정으로 축소
dst1 = cv2.resize(img, (int(width*0.5), int(height*0.5)), interpolation=cv2.INTER_AREA)

## 배율(fx, fy) 지정으로 확대
dst2 = cv2.resize(img, None,  None, 2, 2, cv2.INTER_CUBIC)

img.shape, dst1.shape, dst2.shape
```#결과#```
((120, 98, 3), (60, 49, 3), (240, 196, 3))
````````````

- fx = 2, fy = 2이면 x 축으로 2배, y축으로 2배 스케일링한다는 의미이다.

 

3. 회전(Rotation)

■ 이미지 회전의 경우, 이미지는 2차원 이므로 회전 행렬을 사용하면 된다.

[출처] https://www.youtube.com/watch?v=1oYEo7PNIBQ

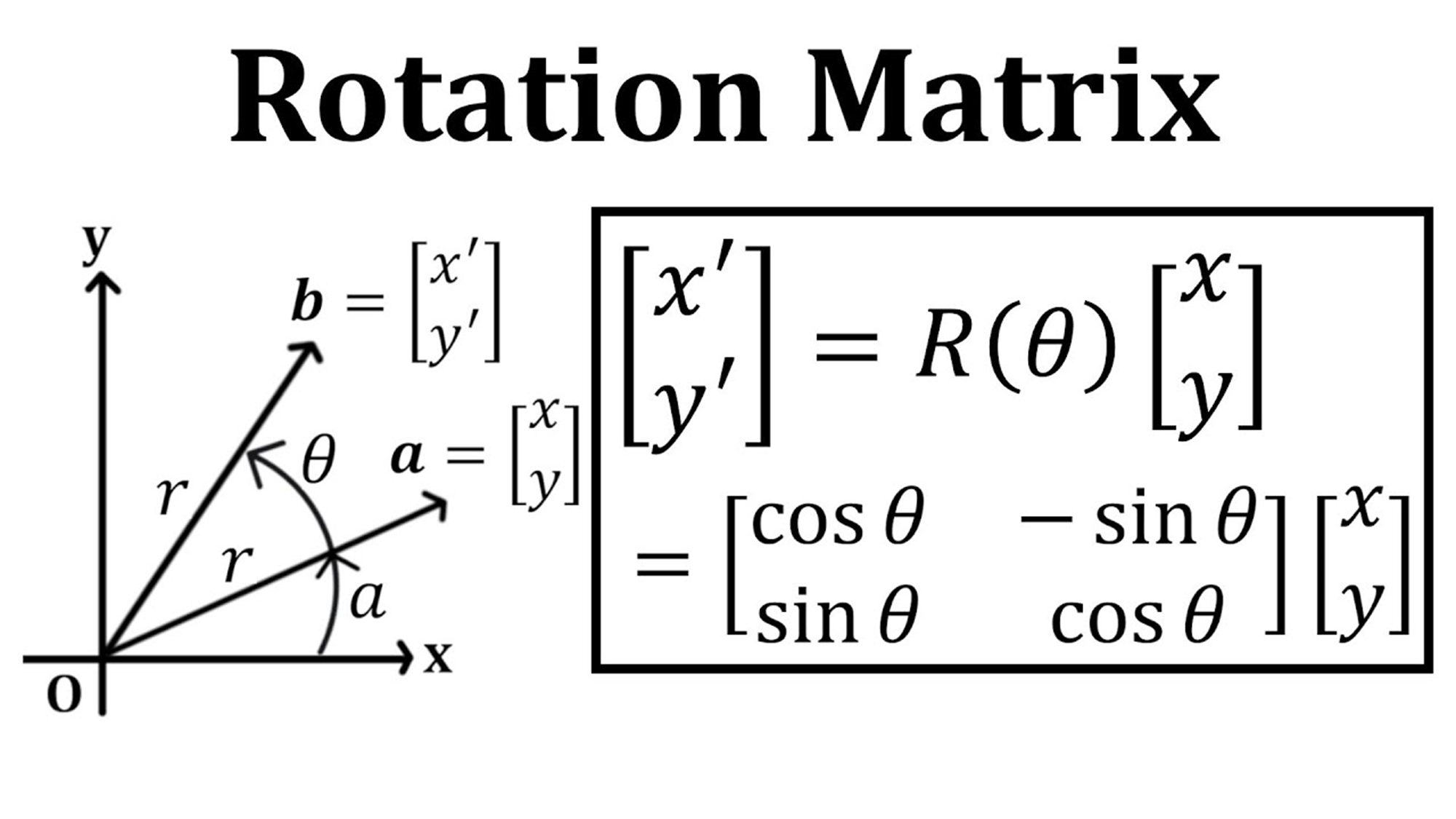
■ OpenCV에서는 cv2.getRotationMatrix2D(center, angle, scale) 함수로 회전 행렬을 생성할 수 있다.
- center는 회전축 중심 좌표 (x, y)
- angle은 회전할 각도 (60 진법)
- scale은 확대/축소 비율

img = cv2.imread('opencv_logo.png')
height, width = img.shape[:2]

## 회전 행렬 정의
# 회전축:중앙, 각도:45, 배율:0.5
rotation_45 = cv2.getRotationMatrix2D((width/2,height/2),45,0.5)
# 회전축:중앙, 각도:90, 배율: 1.5
rotation_90 = cv2.getRotationMatrix2D((width/2,height/2),90,1.5)

## 회전 행렬 적용
img45 = cv2.warpAffine(img, rotation_45, (width, height))
img90 = cv2.warpAffine(img, rotation_90, (width, height))

titles = ['original', 'img45', 'img90']
images = [img, img45, img90]

for i in range(3):
    plt.subplot(1, 3, i+1)
    plt.imshow(images[i][:,:,::-1])
    plt.title(titles[i])
    plt.xticks([]); plt.yticks([])
plt.subplots_adjust(wspace=0.5)
plt.show()

 

4. 어핀 변환(Affine Transform)

■ 이미지를 뒤틀기(왜곡)하는 방법으로 크게 어핀 변환과 원근 변환이 있다.
■ 이 중 어핀 변환은 선의 평행성을 유지하면서 이미지에 이동, 확대/축소, 반전을 적용하는 기법으로, 이를 위해서는 서로 대응하는 3쌍의 점(좌표)이 필요하다.
■ 변환 전, 후의 대응점을 기반으로 변환 행렬을 구할 수 있으며, 변환 행렬을 이용해 이미지를 원하는 형태로 뒤틀 수 있다.

■ OpenCV에서 cv2.getAffineTransform(pts1, pts2) 함수로 어핀 변환의 변환 행렬을 계산할 수 있다.
- pts1은 변환 전 영상/이미지의 좌표 3개 (3 x 2 배열)
- pts2는 변환 후 영상/이미지의 좌표 3개 (3 x 2 배열)
■ 계산된 변환 행렬을 cv2.warpAffine( )에 전달해 주면 어핀 변환이 적용된다.

img = cv2.imread('chessboard.jpg')
rows, cols = img.shape[:2]

## 변환 전, 후 3개의 좌표 생성
pts1 = np.float32([[200,100],[400,100],[200,200]]) # 변환 전 좌표
pts2 = np.float32([[200,300],[400,200],[200,400]]) # 변환 후 좌표(이동 점)

# 변환 전 좌표 표시. Affine 변환 후 이동 점 확인.
cv2.circle(img, (200,100), 10, (255,0,0),-1)
cv2.circle(img, (400,100), 10, (0,255,0),-1)
cv2.circle(img, (200,200), 10, (0,0,255),-1)

## 짝지은 3개의 좌표로 변환 행렬 계산
M = cv2.getAffineTransform(pts1, pts2)
print(M) print(M) # 1열 & 2열이 변형, 3열이 이동의 역할
```#결과#```
[[  1.    0.    0. ]
 [ -0.5   1.  300. ]]
````````````

## 어핀 변환 적용
dst = cv2.warpAffine(img, M, (int(cols*1.3),rows))

plt.subplot(121),plt.imshow(img),plt.title('image'),plt.xticks([]); plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('Affine'),plt.xticks([]); plt.yticks([])
plt.show()

- 어핀 변환은 위의 그림과 같이 3개의 대응점을 이용해서 이미지를 2차원으로 뒤트는 변환이다.

 

5. 원근 변환(Perspective Transform)

■ 원근 변환은 이미지에 원근법의 원리(멀리 있는 것은 작게, 가까이 있는 것은 크게 보임)를 적용하는 방법으로 4개의 대응점을 이용해 이미지를 3차원으로 뒤트는 변환이다.

■ 즉 어핀 변환은 x, y축을 변형했다면, 원근 변환은 x, y, z축을 변형한다.

■ OpenCV에서 cv2.getPerspectiveTransform(pts1, pts2) 함수로 원근 변환의 변환 행렬을 계산할 수 있다.
- pts1은 변환 전 영상/이미지의 좌표 4개 (4 x 2 배열)
- pts2는 변환 후 영상/이미지의 좌표 4개 (4 x 2 배열)
■ 계산된 변환 행렬을 cv2.warpPerspective( )에 전달해 주면 원근 변환이 적용된다.

img = cv2.imread('perspective.jpg')
rows, cols = img.shape[:2]

## 변환 전, 후 4개의 좌표 생성
## 좌표점은 좌상->좌하->우상->우하
pts1 = np.float32([[504,1003],[243,1525],[1000,1000],[1280,1685]]) # 변환 전 좌표
pts2 = np.float32([[10,10],[10,1000],[1000,10],[1000,1000]]) # 변환 후 좌표(이동 점)

## 변환 전 좌표 표시. perspective 변환 후 이동 점 확인.
cv2.circle(img, (504,1003), 20, (255,0,0),-1)
cv2.circle(img, (243,1524), 20, (0,255,0),-1)
cv2.circle(img, (1000,1000), 20, (0,0,255),-1)
cv2.circle(img, (1280,1685), 20, (0,0,0),-1)

## 짝지은 4개의 좌표로 변환 행렬 계산
M = cv2.getPerspectiveTransform(pts1, pts2)
print(M) # 1열 & 2열이 변형, 3열이 이동의 역할
```#결과#```
[[-2.02153837e+00 -1.02691611e+00  2.04001743e+03]
 [-2.24880859e-02 -3.30149532e+00  3.31389904e+03]
 [-2.62496544e-04 -1.74594051e-03  1.00000000e+00]]
````````````

## 원근 변환 적용
dst = cv2.warpPerspective(img, M, (1100,1100))

print(f'변환 전 shape {img.shape}, 변환 후 shape {dst.shape}')
```#결과#```
변환 전 shape (2048, 1536, 3), 변환 후 shape (1100, 1100, 3)
````````````

plt.subplot(121),plt.imshow(img),plt.title('image'),plt.xticks([]); plt.yticks([])
plt.subplot(122),plt.imshow(dst),plt.title('Perspective'),plt.xticks([]); plt.yticks([])
plt.show()

- 실행 결과, 철도 위에서 아래를 보는 것처럼 보인다.

■ 이렇게 원근 변환은 원근 이미지를 평면 이미지로 변환할 수 있으며, 반대로 평면 이미지의 폭을 조절해 원근 이미지로 변환할 수도 있다.

cf) 변환 행렬

[출처] https://devshovelinglife.tistory.com/73

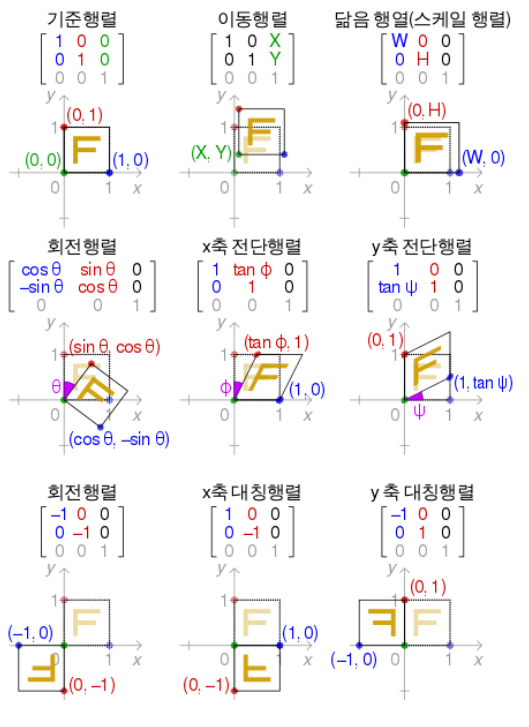
- 3행을 사용하지 않으면 어핀 변환, 3행을 사용하면 원근 변환