1. 층을 깊게 하는 이유
■ CNN 훈련이 끝나면 활성화 맵은 다음 그림과 같이 원본 이미지들의 특징들을 추출해서 가지고 있다. 원본 이미지의 특징을 추출해서 가지고 있는 활성화 맵을 피처 맵(feature map)이라고 한다.

■ CNN 도입부 레이어의 특징 맵은 당연히 중반부, 후반부의 특징 맵보다 사이즈가 크며, 위의 그림과 같이 도입부의 뉴런들은 엣지나 블롭 등의 저수준 특징을 가지고 있다.
■ 중반부의 특징 맵은 중간 사이즈이며, 뉴런들은 얼룩무늬 같은 텍스처에 반응한다. 그리고 분류하기 직전의 후반부 특징 맵은 합성곱 연산이 여러 번 적용되었으므로 사이즈가 작고, 뉴런들은 눈, 얼굴, 바퀴 같은 구체적인 특징에 반응한다.
■ 즉, 계층이 깊어질수록 학습할 문제를 계층적으로 분해해 학습하며 각 계층의 레이어에서 추출되는 정보는 더 추상화된다.
■ 또한, 층이 깊어질수록 뉴런이 반응하는 대상이 단순한 선, 얼룩무늬에서 고급 정보(복잡한 사물의 일부)로 바뀌게 되므로, 이는 점진적으로 사물의 의미(특징)를 이해하는 것으로 볼 수 있다.
■ 예를 들어 고양이를 인식하는 신경망 모델이 있을 때, 신경망의 층이 얕으면 고양이의 특징 대부분을 신경망의 합성곱 계층이 거의 한 번에 이해할 수 있어야 한다.
■ 그러나 실제 고양이들은 품종이 다양해서 털의 색깔, 눈의 크기, 귀의 형태가 다르며, 이미지의 밝기나 어느 각도에서 찍은 것인지에 따라 같은 고양이라도 완전히 다르게 보일 수 있다.
■ 그러므로 층이 얕으면 고양이의 특징을 이해하기 위해 변화가 많은 학습 이미지 데이터가 필요하며, 많은 학습 데이터로 인해 모델의 학습 시간이 기하급수적으로 증가하게 된다.
■ 반면, 층을 깊게 쌓으면 학습해야 할 문제를 계층적으로 분해하기 때문에 CNN의 도입부 레이어는 고양이를 이루는 엣지 패턴 학습에만 전념하도록, 중반부의 레이어는 고양이의 텍스처 패턴 학습에만 전념하도록, 이런 식으로 각 층마다 각각의 패턴 학습에만 전념하도록 만들 수 있다.
■ 즉, 층이 얕으면 각 층이 학습해야 할 문제는 엣지 패턴, 텍스처 패턴 등이 함께 있는 복잡한 문제이며, 층이 충분히 깊으면 각 층이 학습해야 할 문제는 하나의 패턴(단순한 문제)이 되며, 적은 학습 데이터로도 효율적인 학습을 할 수 있다.
■ 고양이라는 패턴보다 고양이의 엣지 패턴의 구조가 훨씬 간단하다. 만약, 처음 층이 엣지 패턴 학습에만 전념한다면 하나의 고양이가 등장하는 이미지에는 고양이를 이루는 수많은 엣지(수많은 가로 엣지, 세로 엣지)가 있기 때문에, 패턴의 구조가 단순한 수많은 엣지 패턴만 학습하더라도 고양이를 유추할 수 있다. 그러므로 적은 학습 데이터로도 충분히 효율적인 학습을 수행할 수 있다.
2. 정확도를 더 높이려면
2.1 작은 크기의 필터를 중첩해서 합성곱 연산
■ 비선형 함수를 적용하면서 층을 깊게 쌓으면 더 복잡한 특징을 학습할 수 있으므로 모델의 표현력이 증가한다.
■ 이는 입력 데이터의 패턴이나 구조에 대해 올바른 학습을 수행한 것이므로 층의 깊이에 비례해 정확도가 좋아질 것으로 기대할 수 있다.
■ 하지만, 층을 깊게 할수록 파라미터의 개수가 많아지므로 역전파 과정에서 그래디언트 소실 문제가 발생할 수 있다.
■ 그러므로 층을 깊게 쌓으면서도 파라미터의 개수를 줄이는 방향으로 모델 구조를 설계해야 하며, 대표적인 방법으로 3 x 3 필터를 중첩하는 방법이 있다. ex) AlexNet, VGG, ResNet 등
■ 예를 들어 다음과 같이 \( 5 \times 5 \) 필터로 구성된 합성곱 계층이 있다고 할 때, 입력 데이터에 \( 5 \times 5 \) 합성곱 연산을 하면 다음과 같이 출력 데이터의 한 점(region feature)을 만들게 된다.

cf) 입력 데이터에 \( 3 \times 3 \) 합성곱 연산을 수행한 예시

■ 이번에는 동일한 크기의 입력 데이터에 \( 3 \times 3 \) 합성곱 연산을 2회 중첩(반복)하는 경우를 생각해보자.
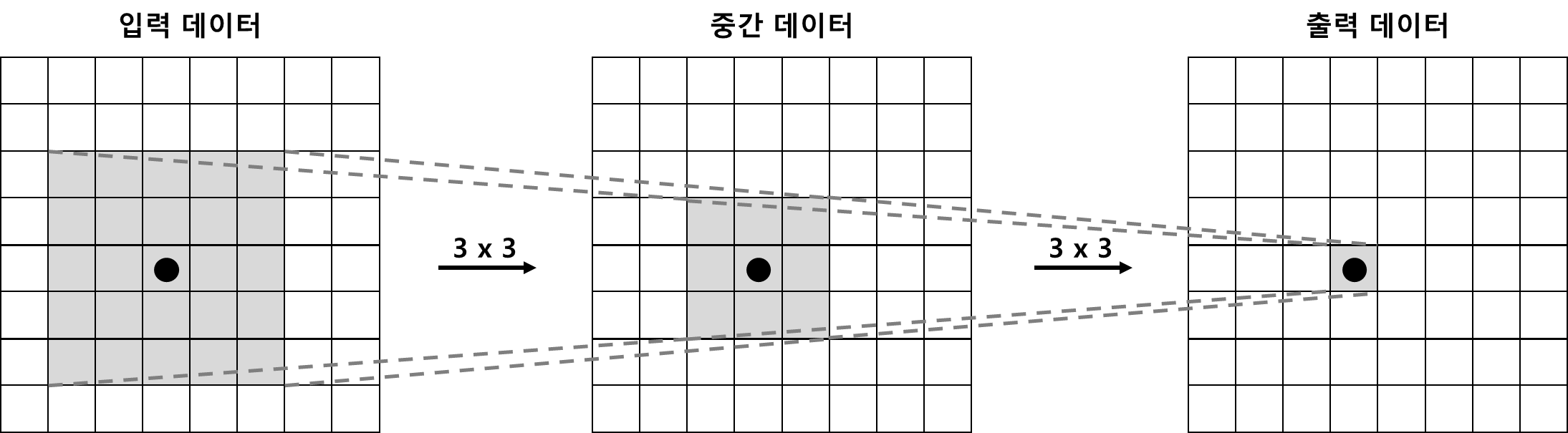
\( 5 \times 5 \) 합성곱 연산 1회와 \( 3 \times 3 \) 합성곱 연산 2회의 결과가 동일한 것을 확인할 수 있다.
■ 이렇게 \( 5 \times 5 \) 합성곱 연산 1회는 \( 3 \times 3 \) 합성곱 연산 2회로 대체할 수 있다. 이때, 매개변수의 수는 \( 5 \times 5 = 25 \)인 반면, 후자는 \( 3 \times 3 = 9 \)가 2번, 즉 \( 3 \times3 \times 2 = 18 \)으로 오히려 \( 3 \times 3 \) 합성곱 연산을 반복할수록 매개변수의 수가 적어지는 것을 알 수 있다. 이 개수의 차이는 층이 깊어질수록 커질 수밖에 없다.
■ \( 7 \times 7 \) 합성곱 연산 1회도 \( 3 \times 3 \) 합성곱 연산 3회 수행으로 대체할 수 있으며, \( 3 \times 3 \) 합성곱 연산을 3번 반복하면 총 매개변수는 27개가 되지만, \( 7 \times 7 \) 합성곱 연산 1회는 같은 크기의 영역에 대해서도 49개의 매개변수가 필요하다.
■ 이렇게 작은 크기의 필터를 겹쳐 합성곱 계층을 깊게 쌓으면 매개변수의 수를 줄이면서 넓은 수용 영역(receptive field)을 소화할 수 있다.
■ 수용 영역은 하나의 뉴런이 원본 이미지에서 담당하는 범위이며, 위의 그림에서 중간 데이터의 검은색 원 뉴런의 수용 영역은 입력 데이터의 \( 3 \times 3 \) 부분이고, 출력 데이터의 검은색 원 뉴런의 수용 영역은 입력 데이터의 \( 5 \times 5 \) 부분이다.
■ 이렇게 수용 영역은 층이 깊어질수록 점차 넓어지고, 초기 레이어에서는 국소적인 저수준 특징(엣지, 블롭 등)을, 층이 깊어질수록 더 넓은 영역에 걸친 고급 정보(사물의 일부, 전체 형태 등)를 인식하게 된다. 이를 통해 CNN은 계층적으로 이미지의 특징 표현을 학습할 수 있는 것이다.
■ 그리고 층을 거듭하면서 ReLU 같은 비선형 함수를 합성곱 계층 사이마다 넣게 되면, 비선형 함수가 겹치면서 신경망의 비선형 능력이 증가하게 되므로 뉴런은 더 복잡한 문제(텍스처, 사물의 일부 등)를 표현할 수 있게 된다. 즉, 신경망의 표현력이 더욱 개선된다.
2.2 학습 이미지 데이터 개수가 부족하면 데이터 증강
■ 학습 이미지 데이터가 많으면, 신경망은 하나의 특징(예를 들어 엣지)에 대해서도 더 다양한 패턴을 학습할 수 있으므로 모델의 정확도가 개선될 수 있다.
■ 가장 보편적인 방법으로 데이터 증강(data augmentation)이 있으며, 입력(원본) 이미지를 프리프로세싱 알고리즘을 통해 이미지를 인위적으로 확장한다.
■ 예를 들어 다음 그림과 같이 이미지를 회전하거나 이동시키는 등의 미세한 변화를 주어 이미지의 개수를 늘린다. 그러므로 학습 이미지 데이터의 개수가 부족할 때 효과적인 방법이다.
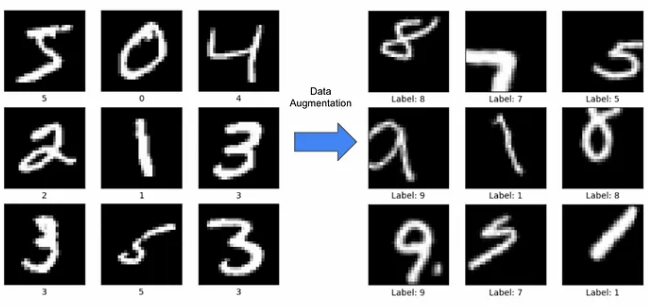
■ 회전, 이동 외에도 이미지 일부를 잘라내는 crop이나, 이미지의 좌우를 반전하는 flip, 밝기를 조절하는 brightness 등의 외형 변화나 이미지 확대/축소 등의 스케일 변화가 있다.
■ 어떤 변화를 적용하든 데이터 증강을 통해 훈련 이미지 데이터의 개수를 늘릴 수 있다면 모델의 성능을 개선할 수 있다.
3. 대표적인 CNN 네트워크 구조
3.1 LeNet
■ LeNet은 최초의 CNN 모델로 Sigmoid 함수를 사용했으며, 32 x 32 크기의 Input과 합성곱 계층 2개, 서브 샘플링 계층 2개, 완전연결 계층 3개로 이뤄져 있다.

■ 위의 그림처럼 합성곱 계층과 서브 샘플링 계층을 반복해서 피처 맵을 생성한 다음, FC 계층을 거쳐 분류를 수행한다.
3.2 AlexNet
■ AlexNet은 입력으로 RGB 3 channel, 224 x 224 크기의 이미지를 사용했으며, 네트워크 구성 면에서 LeNet과 크게 다르지 않다.

■ LeNet과 AlexNet은 Conv 레이어를 반복해서 이미지의 특징을 추출한 다음, 마지막 FC 계층에서 행렬곱 연산으로 차원을 축소한 후 마지막에 Softmax 함수를 사용해 분류를 수행한다.
■ 구성 면에서는 두 모델의 차이가 레이어의 개수 외에 큰 차이가 없어 보이지만, AlexNet은 최초로 Conv 레이어 다음에 사용하는 활성화 함수로 ReLU를 사용했으며, GPU를 이용해서 학습을 진행했다.
■ AlexNet은 다음 그림에서 위쪽 부분은 1번 GPU, 아래쪽 부분은 2번 GPU를 사용해 연산을 수행했다.

■ 위의 AlexNet 구조 그림을 보면 연속으로 3 x 3 필터를 사용한 것을 볼 수 있다.
- 3 x 3 필터를 연속으로 두 번 3 x 3, 3 x 3 사용하면 5 x 5 필터의 효과를
- 3 x 3 필터를 연속으로 세 번 3 x 3, 3 x 3, 3 x 3 사용하면 7 x 7 필터의 효과를 낼 수 있다.
- 이렇게 작은 필터로 큰 필터 효과를 낼 수 있으며, 3 x 3 으로 연산하기 때문에 연산량이 줄어든다.
- 예를 들어 5 x 5 =25인데 5 x 5 효과를 내는 3 x 3 을 두 번 쓰면 3 x 3 + 3 x 3 = 18로 연산량이 5 x 5 보다 더 작다.
■ 이런 테크닉은 신경망 계층이 깊어질수록 효율이 좋아지며, VGGNet에서 이 테크닉을 본격적으로 사용한다.
3.3 VGG
■ 앞서 언급한 것처럼 VGG의 큰 특징은
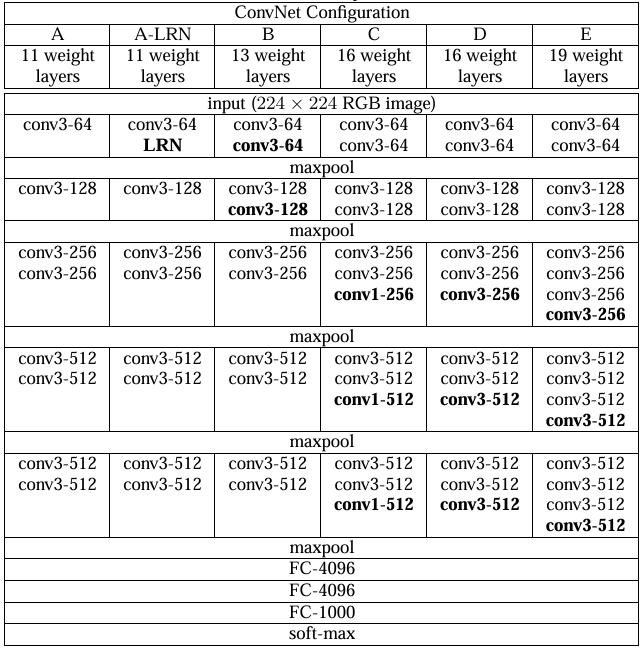

■ 위의 그림에서 볼 수 있듯이, AlexNet과 다른 점은 3 x 3 필터를 더 깊게 중첩해서 사용했다는 점이다.
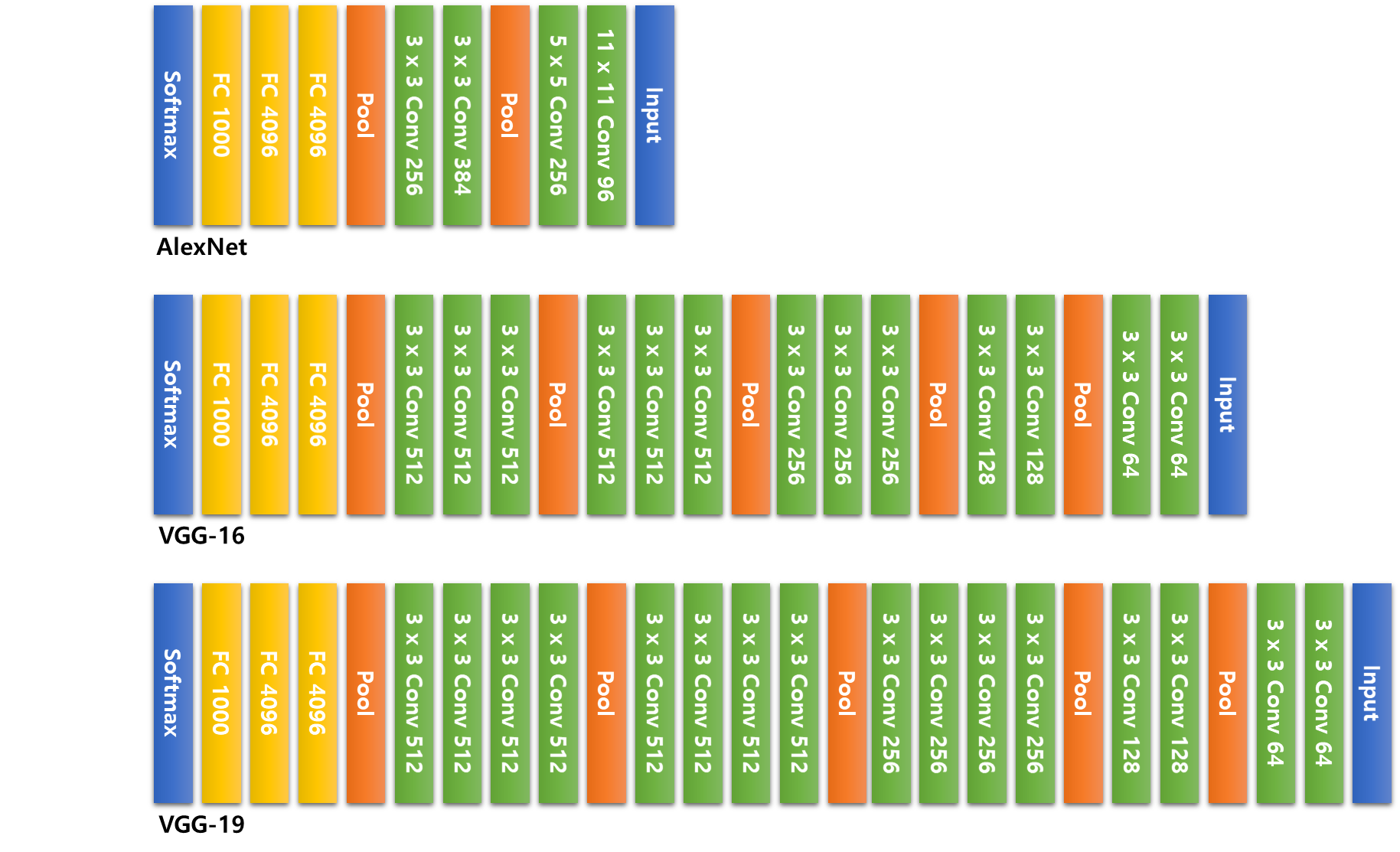
■ 레이어의 깊이에 따라 VGG-16, VGG-19 등으로 불리며, 16개 레이어와 19개 레이어로 구성된 VGG-16, VGG-19가 오류율이 낮아서 많이 사용된다.
- VGG-16은 13개의 Conv 레이어와 3개의 FC 레이어를, VGG-19는 16개의 Conv 레이어와 3개의 FC 레이어를 갖는다.
■ VGG는 위의 그림과 같이 3 x 3이라는 작은 크기의 필터를 단순 중첩하고, 연속으로 풀링 계층을 두어 크기를 절반으로 줄이며 다양한 크기의 이미지에서 특징을 추출(학습)해서 표현력과 정확도를 높였다.
3.4 GoogLeNet
■ 구글에서 제안한 GoogLeNet은 Inception 모듈이라는 개념을 CNN에 도입한 모델로, Inception Model로도 불린다.
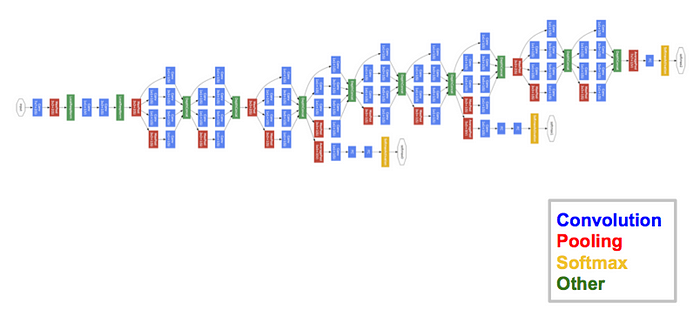
■ GoogLeNet은 22계층으로, 일반 계층 13개와 9개의 Inception Module로 구성돼 있다.
cf) 22개 계층 외에 보조 분류기라고 불리는 계층 2개도 붙어있다.
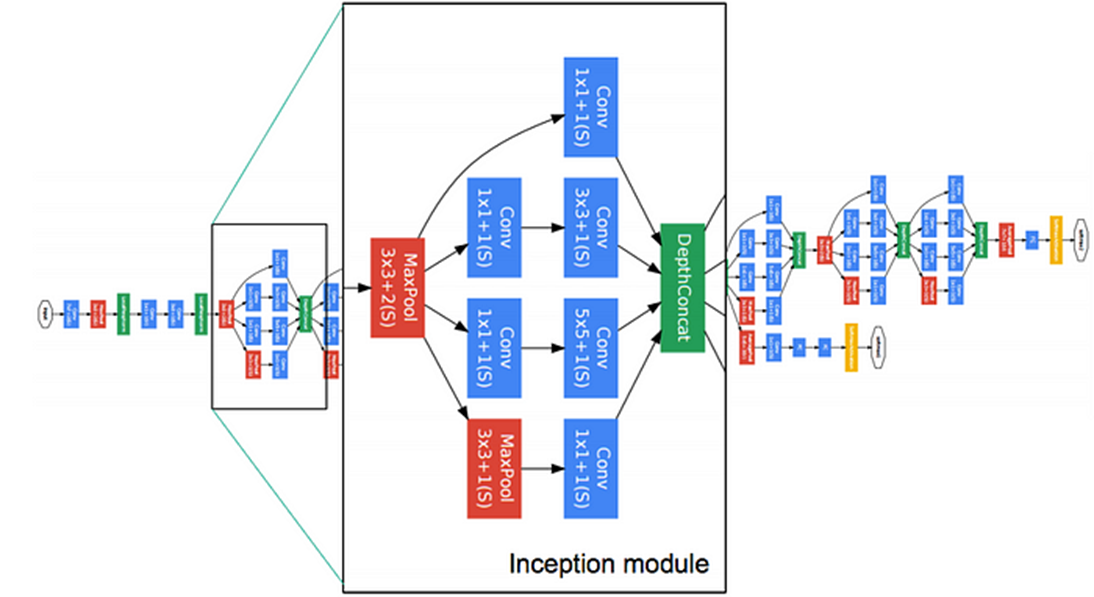
■ Inception은 다음 그림과 같이 다양한 효과를 내기 위해 하나의 레이어 내에서 서로 다른 연산(서로 다른 필터를 적용)을 거친 후 피처 맵을 다시 합치는 방식이다.
(각 필터가 각각의 채널을 만들면, 이 채널들을 결합하는 것이지 하나로 합쳐 섞는 것이 아니다.)

■ 단, 이런 단순한 인셉션 모듈의 문제는 연산 비용이다.
■ 예를 들어 위의 GoogLeNet 인셉션 모듈 부분에서 원래의 단순한 인셉션 모듈은 1 x 1 Conv가 없는 구조이다.

■ 여기서 이전 층의 출력 결과가 28 x 28 x 192, 다음 Conv 레이어의 크기가 28 x 28 x 32이고 필터 크기가 5 x 5일 때의 연산량을 계산해 보면 연산량은 28 x 28 x 192 x 5 x 5 x 32 = 120,422,400 약 1억 2천만이 된다.
■ 이와 같은 상태로 레이어를 쌓으면, 파라미터의 개수가 많아진다. 파라미터의 개수가 많아지면 많은 연산으로 오버피팅이 일어날 가능성이 커지며, 역전파 과정에서 레이어의 가중치들의 미분 값이 중첩되어 곱해지므로 기울기가 0에 수렴하는 그래디언트 소실 문제가 발생하게 된다.
■ GoogLeNet은 이런 문제를 해결하고자 1 x 1 컨볼루션 레이어를 적용하여 이미지의 공간 차원(이미지의 가로, 세로)은 유지하면서 채널 수를 줄여 차원을 축소해서 연산량을 줄였다.
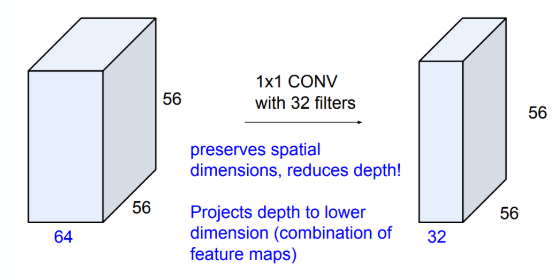
■ 예를 들어 1 x 1 컨볼루션 레이어를 적용한 GoogLeNet의 인셉션 모듈에서 위에서 연산량을 계산한 부분만 다시 연산량을 계산해 보자.

■ 먼저, 이전 계층의 피처 맵과 1 x 1 Conv 레이어의 연산량은 28 x 28 x 192 x 1 x 1 x 16 = 2,408,448
■ 그리고 다음 층과의 합성곱 연산은, 입력 채널의 수 16, 출력 채널의 수 32, 이미지의 크기가 28 x 28, 필터 크기가 5 x 5이므로 연산량은 28 x 28 x 16 x 5 x 5 x 32 = 10,035,200이 된다.
■ 따라서 총 연산량은 2,408,448 + 10,035,200 = 12,443,648로 위에서 1 x 1 Conv 레이어를 포함하지 않고 바로 합성곱을 진행한 연산량 120,422,400보다 약 1/10 정도의 연산량이 줄어든 것을 확인할 수 있다.
■ 1 x 1 컨볼루션은 ReLU와 함께 쓰이면 원본 이미지(혹은 이전 피처 맵)와 유사한 특징을 가진 데이터에 ReLU를 적용해 더 많은 비선형성이 도입되므로 신경망의 표현력을 향상하는 데 사용한다. GoogLeNet은 이 1 x 1 컨볼루션을 차원 축소 용도로 사용한 것이다.
■ 1 x 1 컨볼루션을 적용한 인셉션 모듈을 연속으로 쌓은 것이 바로 GoogLeNet이다.
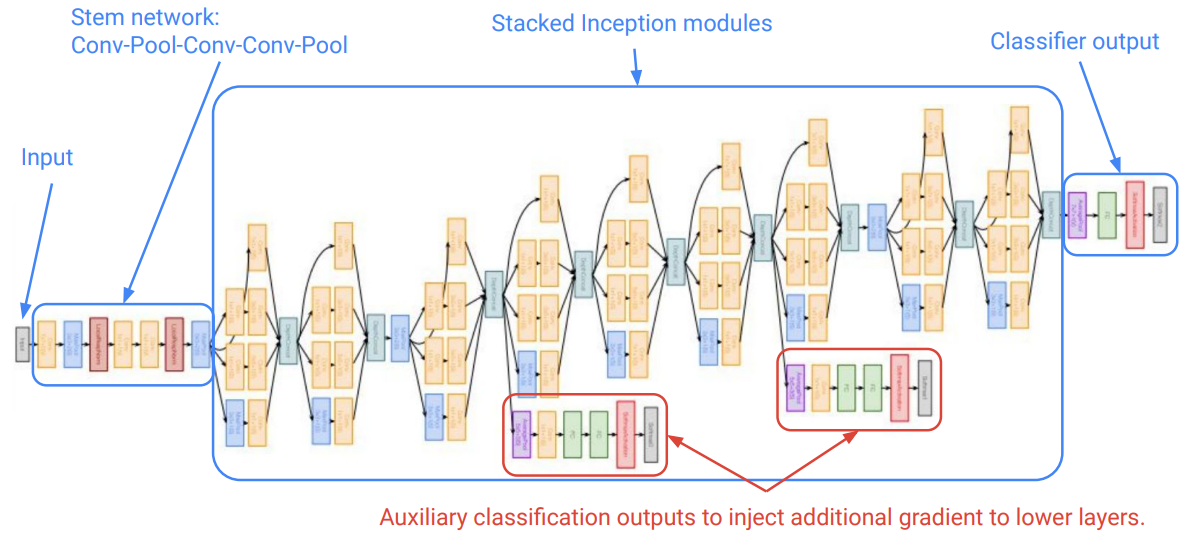
- 기본적인 신경망 모델은 하나의 분류-손실 계층(주 분류기)에서 역전파를 하기 때문에 마지막 부분(상위 층)에서 맨 앞 부분(하위 층)까지의 모든 기울기가 곱해지므로 그래디언트 소실 문제를 피하기 어렵다.
- 반면, GoogLeNet은 2개의 보조 분류기를 추가해 인셉션 모듈 중간중간에 손실을 계산하므로 역전파 과정에서 하나의 분류-손실 계층(주 분류기)에서 전파되는 기울기 값들을 하위 층까지 연속적으로 전달하지 않고,
- 중간에 위치한 보조 분류기들이 추가적인 역전파 경로를 만들어 더 짧은 경로로 하위 층까지 그래디언트를 전달하기 때문에 그래디언트 소실 문제를 완화하는 데 도움을 줄 수 있다.
cf) GoogLeNet의 최종 손실 값은 2개의 분류 보조기에서 산출된 2개의 손실 값과 주 분류기에서 산출된 손실 값의 평균이다.
■ GoogLeNet은 1 x 1 컨볼루션을 적용한 인셉션 모듈을 통해 8계층인 AlexNet보다 12배 적은 파라미터로 그래디언트 소실 문제를 억제하며, 하나의 피처 맵에서 여러 컨볼루션 연산을 적용해 작은 규모의 피처와 큰 규모의 피처를 한 번에 추출(학습)하는 장점을 가지게 되었다.
■ GoogLeNet의 또 다른 특징은 네트워크 마지막에 FC 레이어를 GAP(Global Average Pooling)으로 대체해 파라미터 수를 크게 줄였다는 점이다.
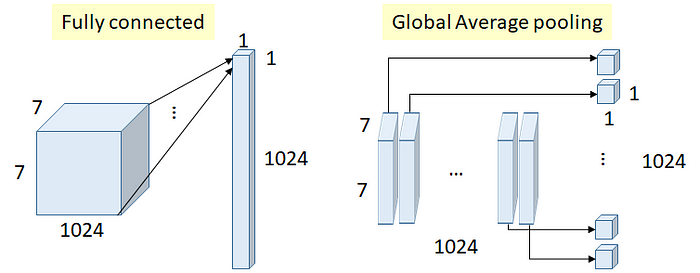
■ 기본적으로 사용하던 구조인 CNN + FCN에서 CNN은 이미지의 특징을 추출(학습)하는 것이라면, FCN은 CNN의 최종 피처 맵을 평탄화시킨 1차원 벡터를 입력으로 받아 분류 결과를 반환하다.
■ FCN은 완전연결 계층이기 때문에 전체 CNN보다 더 많은 파라미터를 가지며 출력층에서 Softmax 함수를 사용할 경우 지수함수 계산도 해야 하기 때문에 계산이 오래 걸린다.
■ GoogLeNet은 FC 계층 대신, 마지막 피처 맵에 대해 평균 풀링을 연결해 피처 맵의 각각의 값을 평균내는 풀링 방식으로 피처(특징) 맵의 특징을 효과적으로 추출할 뿐만 아니라 오버피팅도 피할 수 있다.
■ 예를 들어 위의 그림에서 FC 레이어에서는 7 x 7 x 1024의 입력층으로부터 1 x 1024의 벡터를 출력하기 위해 필요한 파라미터 수는 7 x 7 x 1024 x 1024 = 51,380,224 개이다.
■ 반면, GAP은 7 x 7 크기의 특징 맵을 평균해 얻은 1 x 1 값을 1024번 수행해 나열하는 것이므로 필요한 가중치의 파라미터 개수는 0 개이다.
3.5 ResNet
■ CNN의 계층들은 복잡한 특징을 점진적으로 학습하기 때문에 신경망의 깊이가 깊을수록 성능 향상에 도움이 된다.
■ 그 이유는, 하위 층에서 상위층으로 학습 과정을 진행할 때, 이미지의 엣지, shape, object, 구체적인 특징을 점진적으로 학습하기 때문이다. 즉, 층이 깊은 모델은 뉴런이 반응하는 대상이 단순한 모양에서 '고급 정보로 변환되기 때문이다.
■ 하지만, 신경망의 깊이가 어느 정도를 넘어가면 그래디언트 소실이 발생해 기존 CNN은 최종 손실 값이 최소가 되는 지점을 찾아갈 수 없다. 즉, 제대로 된 학습을 할 수 없다.
■ ResNet은 이런 그래디언트 소실 문제를 '스킵 연결(Skip Connection) 또는 숏컷 연결(Shortcut Connection)이라고 하는 하나 이상의 레이어를 건너뛰는 연결'을 이용한 '잔차 학습( Residual learning)'을 통해 극복하고자 고안되었다.
■ ResNet은 다음과 같은 'Residual block'이라는 개념을 도입했다. Residual block은 이전 레이어의 피처 맵을 다음 레이어의 피처 맵에 더해주는 개념이며, 이를 'Skip Connection'이라 한다. 이 구조가 층의 깊이에 비례해 성능을 향상시킬 수 있게 한 핵심이다. 물론 층을 깊게 하는 데는 여전히 한계가 있다.
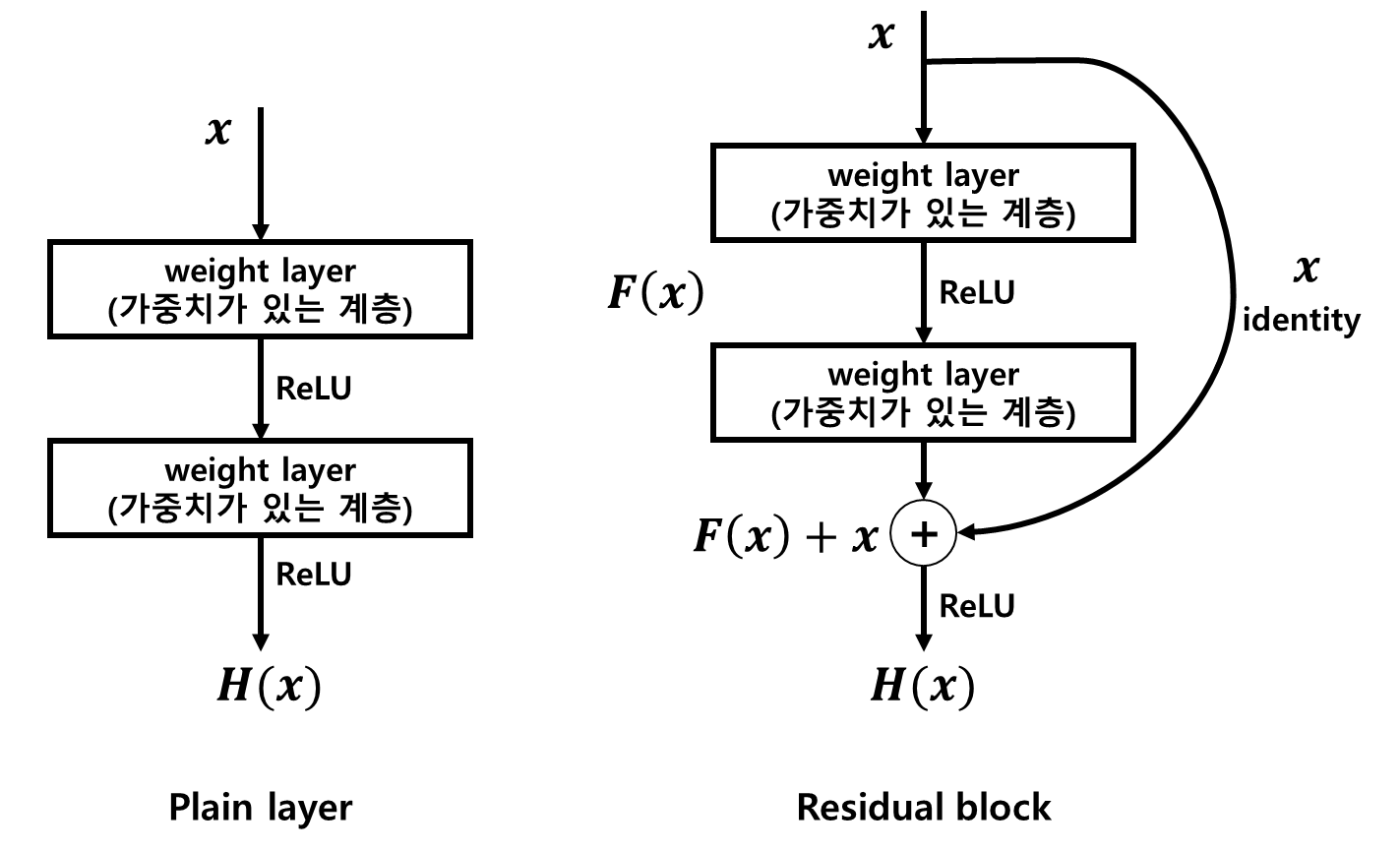
■ 기존 신경망의 학습 목적은 입력값 \( x \)를 타겟값 \( y \)로 매핑해주는 (입력값 \( x \)를 타겟값 \( y \)로 변환해 주는) 함수 \( H(x) \)를 찾는 것이다. 즉, \( x \)를 \( H( ) \)에 넣었을 때 \( H(x) = y \)가 되는 \( H(x) \)를 찾는 것이 기존 신경망의 학습 목적이다.
■ 예를 들어 입력값 \( x \)가 고양이 사진이라면, 이미지의 픽셀 값들이 입력 \( x \)가 된다. 그리고 이 \( x \)에 대한 타겟값 \( y \)가 1이라면 신경망의 학습 목적은 \( H(x) \)가 \( y = 1 \)로 매핑 되도록 만드는 것이다.
■ 즉, \( H(x) = y \Longleftrightarrow H(x) - y = 0 \), \( H(x) - y \)값이 0이 되도록, \( H(x) - y \)를 최소화하는 것이 기존 신경망의 학습 목적이다.
■ 반면, ResNet은 skip connection이라는 단축 경로로 가중치가 있는 계층을 건너 뛰어 입력값 \( x \)를 출력 \( F(x) \)에 직접 더하는 구조로 타겟값 \( y \)가 입력값 \( x \)에 매핑 되도록 훈련한다.
■ 즉, 입력값 \( x \)가 출력값 \( H(x) \)와 최대로 매핑 되도록 훈련하는 것이 ResNet이며, \( F(x) + x = H(x) \)라는 수식에서 \( x \)와 \( H(x) \)가 최대로 매핑되기 위해서는 \( F(x) = 0 \), 즉 \( F(x) \)가 최소가 되도록 학습해야 한다.
■ \( F(x) + x = H(x) \Longleftrightarrow F(x) = H(x) - x \)로 표현한다면 \( F(x) \)는 '출력값과 입력값의 차'이며, \( F(x) \)가 최소가 되도록 학습한다는 것은 결국, 출력값 \( H(x) \)와 입력값의 차 \( H(x) - x \)를 최소화하기 위한 학습을 해야 한다는 것이다.
■ 실제 값인 입력 \( x \)와 그 입력의 출력값인 \( H(x) \)의 차이므로 이는 '잔차(residual)'이며, 이 잔차를 학습시켜야 하기 때문에 잔차 학습이라고 한다.
■ 이 잔차 학습을 통해 역전파 과정에서 그래디언트가 0에 수렴하는 그래디언트 소실 현상을 완화할 수 있다.
■ 왜냐하면 스킵 연결로 입력과 출력값이 동일한 아이덴티티 매핑(identity mapping)을 수행해서 \( F(x) + x = H(x) = x \)가 되도록 학습시키면, 즉 \( F(x) + x \)에서 \( F(x) = 0 \)이 되도록 학습시키면 \( F(x) + x \)를 미분했을 때 \( F'(x) + 1 \)이기 때문에 각 레이어의 그래디언트가 최소 1이 된다.
■ 여기에서 핵심은 스킵 연결로 입력 데이터(혹은 이전 층의 출력)에 아무런 수정도 가하지 않고 '그대로' 입력 데이터를(혹은 한 층의 출력을) Top 층(더 깊은 층)에 흘려보내므로, 역전파 과정에서도 Top 층으로부터의 기울기를 그대로 하류로 보내게 된다. 그러므로 기울기가 작아지는 문제를 완화하는 것뿐만 아니라 '의미 있는 기울기'가 하류로 전해지리라 기대할 수 있다.
■ 이러한 스킵 연결(숏컷 연결)로 만든 블록을 아이덴티티 블록(identity block)이라고 하며, 입력 \( x \)에 컨볼루션을 연산한 후 \( F(x) \)에 더하는 형태를 컨볼루션 블록(convolution block)이라고 한다. ResNet은 아이덴티티 블록과 입력 \( x \)에 1 x 1 컨볼루션 연산을 한 후 \( F(x) \)에 더하는 1 x 1 컨볼루션 블록으로 구성된다.


■ ResNet은 VGGNet의 중첩된 3 x 3 필터의 아이디어를 기반으로 3 x 3 컨볼루션을 기본으로 사용하는 플레인 네트워크를 만들었다. 이 플레인 네트워크는 다음과 같은 규칙을 따른다.
- (1) 같은 피처 맵의 경우 필터 수가 같다.
- (2) 피처 맵의 크기가 절반으로 줄어들면 각 레이어의 시간 복잡성을 유지하기 위해 필터 수가 두 배가 된다.
- (3) 분류를 위해 GAP과 하나의 FC 계층을 사용한다.
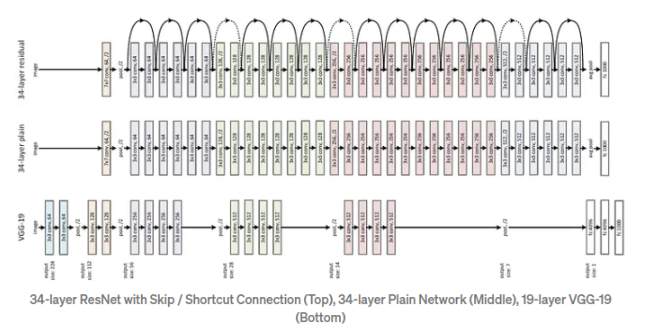
■ 이 플레인 네트워크를 기반으로 두 장의 레이어마다 숏컷 연결이 삽입되어 잔차 블록들이 적용된 네트워크가 바로 ResNet이며, 입력과 출력의 차원이 동일한 경우 아이덴티티 블록을 사용할 수 있다.
■ 만약, 차원이 증가하면 입력 \( x \)와 출력 \( H(x) \)의 차원을 맞춰주기 위해 두 가지 옵션을 고려한다.
- (1) 차원을 늘리기 위해 제로 패딩(padding)을 적용하고 아이덴티티 매핑을 수행
- (2) 차원을 일치시키기 위해 1 x 1 컨볼루션 블록 사용
■ 여기서 1 x 1 컨볼루션 블록은 예를 들어 다음 그림과 같이 입력이 28 x 28 x 256이라면 앞에서 1 x 1 x 64로 피처 맵의 차원을 줄인 다음, 마지막에 입력과 출력의 차원을 맞추기 위해 1 x 1 x 256 컨볼루션 연산을 수행한다.

이렇게 차원을 일치시키는 이유는 \( H(x) = F(x) + x \)에서 \( + \) 연산을 하기 위해서는 차원이 동일해야 하기 때문이다.
'딥러닝' 카테고리의 다른 글
| 순환 신경망(RNN) (2) (0) | 2025.01.06 |
|---|---|
| 순환 신경망(RNN) (1) (0) | 2025.01.06 |
| word2vec 속도 개선 (1) (0) | 2024.11.27 |
| 단어의 의미를 파악하는 방법 (4) (0) | 2024.11.22 |
| 단어의 의미를 파악하는 방법 (2) (0) | 2024.11.21 |



