■ autoregressive decoding 방식은 각 step이 이전 step들의 output에 의존하는 순차적인 계산 방식이다.
■ 즉, 다음 토큰을 생성하기 위해 이전 step에 생성된 모든 토큰을 입력으로 받아야 한다.
■ 이를 위해 매 디코딩 단계마다 수십억 개의 파라미터를 HBM에서 SRAM으로 이동시킨 다음 계산을 해야 하는데, HBM의 데이터를 이동시키는 속도가 느리기 때문에 병목 현상이 발생한다.
■ 이 문제를 해결하기 위해 speculative decoding과 같은 방법들이 제안되었지만, 적절한 draft model을 확보하고 유지 관리해야 하는 어려움으로 실제 적용이 쉽지 않다.
■ 그래서 이 논문에서는 여러 후속 토큰을 병렬로 예측하기 위해 추가적인 디코딩 헤드(decoding heads)를 더하여 LLM 추론을 증강하는 방법인 Medusa를 제안한다. 트리 기반 어텐션 메커니즘을 사용하여, Medusa는 여러 후보 연속 문장을 구성하고 각 디코딩 단계에서 이를 동시에 검증한다.
■ 그리고 다양한 use cases을 고려하여 Medusa에 대한 두 가지 fine-tuning procedures를 제시한다.
- (1) Medusa-1: frozen된 backbone LLM 위에서 Medusa head만 파인튜닝하기. 원본 모델의 파라미터가 변하지 않으므로 loss 없는 추론 가속을 보장한다.
- (2) Medusa-2: backbone LLM과 Medusa head를 함께 파인튜닝하기. Medusa head의 예측 정확도를 높이고 더 높은 속도 향상을 가능하게 한다. 단, 원본 모델의 성능이 저하되지 않도록 특별한 레시피가 필요하다.
■ 또한, training data를 사용할 수 없는 상황을 처리하기 위한 self-distillation과 생성 품질을 유지하면서 acceptance rate를 높이기 위한 전형적인 acceptance 방식(예: 기존의 기각 샘플링을 수정한 방식)을 포함하여, Medusa의 유용성을 개선하거나 확장하는 몇 가지 확장을 제안한다.
[2401.10774] Medusa: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads
Medusa: Simple LLM Inference Acceleration Framework with Multiple Decoding Heads
Large Language Models (LLMs) employ auto-regressive decoding that requires sequential computation, with each step reliant on the previous one's output. This creates a bottleneck as each step necessitates moving the full model parameters from High-Bandwidth
arxiv.org

1. Introduction
■ LLM의 최근 발전은 모델 크기가 수십억 개의 파라미터에 도달함에 따라 언어 생성 품질이 크게 향상(예: GPT-3)됨을 입증하였다. 그러나 이러한 성장은 inference latency의 증가로 이어진다.
■ 시스템 관점에서 LLM의 inference는 memory-bound를 받으며, 주요 latency 병목은 산술 연산보다는 메모리 대역폭(메모리 읽기/쓰기)에서 기인한다.
■ 각 forward pass는 HBM에서 SRAM으로 모델 파라미터를 전송해야 한다. 단 하나의 토큰만 생성하는 auto-regressive decoding의 순차적인 특성은 최신 GPU의 산술 연산 잠재력을 충분히 활용하지 못하여 결과적으로 비효율성을 초래한다.
■ 이러한 비효율성을 완화하기 위한 일반적인 방법으로 배치 크기를 늘려 더 많은 토큰을 병렬로 생성하는 것이 사용되었다. 배치 크기를 늘려 throughput를 늘리려는 것인데, 이 방법은 latency를 증가시킬 뿐만 아니라, KV-cache에 대한 메모리 요구량도 크게 증가시킨다.
■ 그래서 배치 크기를 늘리는 방법은 throughput과 latency의 trade-off가 존재하므로, 낮은 지연 시간이 필수적인 많은 애플리케이션에서 사용하기에 비현실적이다.
■ LLM의 추론 속도 향상, 즉 텍스트 생성을 가속화하기 위한 전략 중 하나는 디코딩 과정의 연산 효율성을 높이는 것이며, 이 지점에서 등장한 것이 디코딩 과정의 연산은 늘리고 디코딩 단계 수를 줄이는 것을 목표로 하는 "speculative decoding"이다.
■ speculative decoding은 작은 크기의 draft model을 사용하여 토큰 시퀀스를 빠르게 생성한 다음, draft model보다 더 큰 model이 생성된 토큰들을 병렬로 효율적으로 검증함으로써 연산 처리량(throughput)을 극대화할 수 있다.
- 잘 조율된 draft model(target model의 수락률을 높일 수 있는 성능 좋은 draft model)을 사용할 경우, speculative decoding은 최대 2.5배까지 latency를 단축할 수 있다.
■ 그러나 이 접근 방식에도 어려움이 없는 것은 아니다.
- (1) 적절한 draft model(target model과 잘 부합하는, 작지만 강력한 model)을 확보하는 것은 쉽지 않다.
- (2) 하나의 시스템에 두 개의 서로 다른 모델인 draft model과 target model을 분산 환경에서 사용(연산 및 운영)하는 것은 더욱 어렵다.
- (3) speculative decoding으로 샘플링을 수행할 때는 importance sampling 기법(본래의 확률분포 \( p \)가 아닌, 다른 확률분포 \( q \)에서 추출된 샘플들을 이용하여 기댓값을 계산하는 방법)을 사용해야 한다. 이는 생성 과정에서 추가적인 overhead를 발생시킨다.
- ① speculative decoding의 수락/기각 규칙 \( \min(1, p(x) / q(x)) \)이 바로 importance sampling의 원리를 적용한 것이다.
- 이때 \( p(x) / q(x) \)를 importance weight라고 부르며, 이는 \( q(x) \)로부터 샘플링을 수행하여 기댓값을 계산했을 때 발생하는 에러를 보정하는 역할을 한다.
- speculative decoding은 이 importance weight를 이용해서(\( p \)가 \( q \)보다 큰 경우, \( p \)가 \( q \)보다 작은 경우를 고려하여) \( q(x) \)의 결과를 보정하고 최종 결과가 \( p(x) \)의 분포를 따르도록 만든다.
- 이렇게 보정 과정, 즉 importance sampling을 수행하는 것 자체가 추가적인 계산 비용을 유발한다.
- ② 특히, 높은 temperature를 사용할 경우 확률분포가 평평해져서, 원래는 확률이 낮은 토큰들이 선택될 가능성이 높아져 더 다양하고 창의적인 토큰이 생성되기 때문에 draft model과 target model의 판단이 일치하지 않을 가능성이 높아진다.
- 즉, 기각할 가능성이 높아지고 기각이 발생하면 리샘플링을 해야 하기 때문에, 높은 temperature를 사용할 경우 계산 비용이 더 높아진다.
- 다시 말해, temperature를 높일수록 기각이 잦아지고, 기각이 잦아질수록 리샘플링 오버헤드가 커져서 speculative decoding의 속도 향상 효과가 상쇄되거나 오히려 더 느려질 수 있다.
■ 위와 같은 복잡성과 trade-off로 speculative decoding은 기술이 유망함에도 불구하고, 널리 채택되지 못하였다.
■ 그래서 이 논문에서는 별도의 draft model을 사용하여 candidate outputs을 생성하는 대신, 추론을 가속화하기 위해 backbone model 위에 "Medusa heads", multiple decoding heads를 붙여 model을 확장한다.
■ 이 heads은 파라미터 효율적인 방식으로 파인튜닝되며 기존 모든 모델에 추가될 수 있다. heads만 추가하기 때문에 VRAM 사용량이 draft model을 로드하는 것보다 훨씬 적으며, LM의 head와 유사하게 단 하나의 레이어로 구성되어 있어 분산 환경에서도 사용하기 쉽다.
■ 저자들은 다음과 같은 두 가지 인사이트를 바탕으로 Medusa를 더 발전시켰다.
- (1) 각 decoding step에서 하나의 candidate를 생성하는 접근 방식은 계산 자원의 비효율적인 사용으로 이어진다.
- 이를 해결하기 위해 Medusa heads을 사용하여 여러 개의 candidate들을 생성하고, attention mask에 대한 간단한 조정을 통해 이들을 동시에 검증한다.
- (2) original model(target model)과 동일한 분포를 가진 응답을 생성하기 위해 speculative decoding에서 사용되는 rejection sampling 방식을 사용할 수 있지만, 이 방식은 가속률을 더 이상 향상시킬 수 없다.
- 대안으로, Medusa head outputs에서 합리적인 candidate를 선택하는 acceptance 방식을 도입한다.
■ 그리고 LLM에 Medusa heads을 장착할 때, 시나리오에 따른 두 가지 파인튜닝 절차를 제안한다.
- (1) 계산 자원이 제한적이거나 성능에 영향을 주지 않고 기존 모델에 Medusa를 통합하는 것이 목표인 상황에서는 Medusa-1을 권장한다.
- 이 방법은 백본 모델이 frozen되어 있기 때문에 생성 품질을 저하시키지 않으며, 최소한의 메모리만을 필요로 한다. 또한 QLoRA 같은 양자화 기술로 더욱 최적화될 수 있다.
- 단, Medusa-1에서는 backbone model을 frozen하기 때문에, backbone model의 잠재력이 완전히 활용되지 않는다.
- (2) 충분한 계산 자원이 있는 환경이나 기본 모델로부터 직접적인 SFT(Supervised Fine-Tuning)을 수행하는 데 Medusa-2가 적합하다.
- Medusa-2는 모델의 next token 예측 능력과 출력 품질을 손상시키지 않으면서 Medusa heads와 backbone model을 함께 training하는 방법이다.
- Medusa head를 training하기 때문에 Medusa head의 예측 정확도를 더 높일 수 있고, 이는 더 큰 속도 향상으로 이어질 수 있다. 단, backbone model이 업데이트로 변형되면서 그 성능을 잃지 않도록 하는 특별한 recipe가 필요하다.
■ 또한, 모델의 training recipe와 training dataset을 확보하기 위한 다양한 전략을 제안한다.
- (1) 모델이 공개 데이터셋에서 파인튜닝된 경우, 이를 Medusa에 직접 사용할 수 있다.
- (2) 데이터셋을 사용할 수 없거나 모델이 인간 피드백 기반 강화 학습(RLHF) 과정을 거친 경우, Medusa heads을 위한 training dataset을 생성하기 위한 self-distillation 접근법을 제안한다.
■ 논문의 실험은 주로 배치 크기가 1인 시나리오에 초점이 맞춰져 있다. 이 설정은 LLM이 개인 용도로 로컬에서 호스팅되는 use case를 가정한 것이다.
■ Vicuna-7B, 13B (trained with a public dataset), Vicuna 33B (trained with a private dataset), Zephyr-7B(trained with both supervised fine-tuning and alignment)를 포함한 다양한 크기와 training setting을 가진 모델들에서 Medusa를 테스트한다.
2. Methodology
■ speculative decoding에서 subsequent token들은 draft model에 의해 예측된다. 이 draft model은 original model이 수락할 만한 토큰들을 생성할 수 있을 만큼 효과적이면서도 작은 크기여야 한다.
■ 또한, draft model과 original model을 분산 환경에서 서빙해야 한다. 그러나 이러한 요구사항들을 충족하는 것은 어려운 문제이다.
■ 기존 접근 방식은 더 작은 모델을 별도로 pre-training한 모델을 사용한다. 이는 별도의 pre-training 과정이 추가되어 상당한 계산 자원이 추가로 요구된다.
■ 그리고 이 방식은 별도의 pre-training을 진행하기 때문에, pre-trained draft model이 학습한 데이터 분포와 original model의 분포가 달라지므로, original model이 선호하지 않는 토큰들을 생성할 수 있다.
■ Medusa는 speculative decoding과 동일한 프레임워크를 따르며, 각 디코딩 단계는 세 가지 substeps "(1) candidates 생성 (2) candidates 처리 (3) candidates 수락"으로 구성된다. 전체 파이프라인은 Fig 1과 같다.

■ Medusa에서 (1)은 Medusa heads에 의해 달성되고 (2)는 tree attention에 의해 처리된다.
■ 이때, Medusa heads은 original model의 위에 있기 때문에, (2)에서 계산된 logits은 next decoding step의 substep (1)을 위한 입력으로 재활용될 수 있다.
■ (3)은 rejection sampling 또는 typical acceptance (섹션 2.3.1)에 의해 처리될 수 있다.
2.1 Key Components
2.1.1 MEDUSA HEADS
■ Medusa heads은 original model의 last hidden states에 추가되는 별도의 decoding heads이다.
- 즉, Medusa heads는 다음 그림과 같이 original model의 original lm(language model) head에 추가되는 별도의 decoding head들이다.
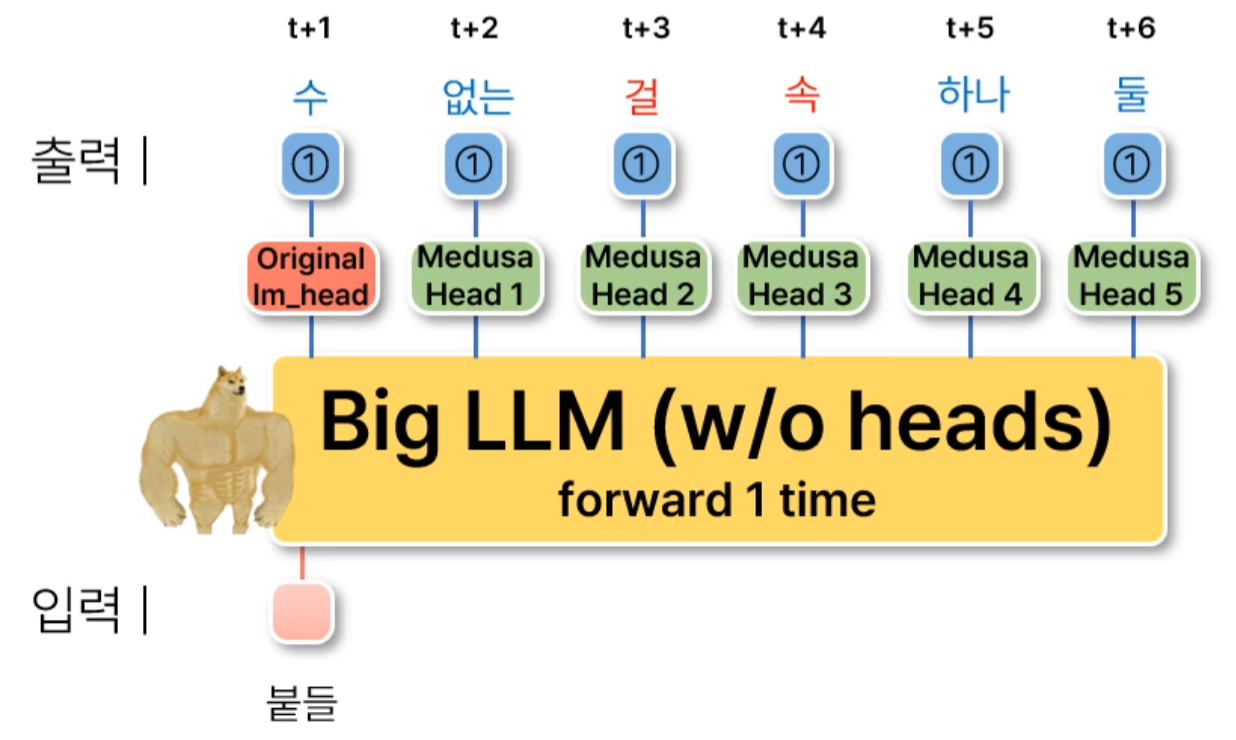
■ 구체적으로, original model의 \( t \) 번째 last hidden states \( h_t \)가 주어지면, \( h_t \)에 \( K \)개의 decoding heads을 추가한다.
■ \( K \)번째 head는 \( t+K+1 \)번째 위치에 있는 next token을 예측하기 위해 사용된다.
- 위의 그림은 \( K = 5 \)일 때의 예시이다.
- original model의 original lm head는 위의 그림처럼 \( t+1 \)번째 token을 예측하는 데 사용된다.
- \( t \)번째 last hidden states에 대해 \( t+k+1 \) 시점을 예측하는 \( k \)번째 Medusa head를 학습시킨다.
■ 논문에서는 \( k \)번째 head의 예측은 \( p_t^{(k)} \)로, original model의 예측은 \( p_t^{(0)} \)으로 표기한다. 이는 vocabulary에 대한 분포를 의미한다.
■ \( k \)번째 head의 정의는 다음과 같다.

- 여기서 \( d \)는 LLM의 last hidden layer의 output dimension이고, \( V \)는 vocabulary size이다.
- 각 head에 대해 residual connection이 있는 단일 층 피드포워드 네트워크를 활용한다. 이 간단한 설계가 좋은 성능을 달성한다는 것을 발견하였다.
- Llama model들을 따라 SiLU activation function을 사용하였다. \( SiLU(x) = x \cdot \sigma (x) \)이며, 이때 \( \sigma \)는 sigmoid function이다.
■ \( W_2^{(k)} \)를 original lm head와 동일하게 초기화하고, \( W_1^{(k)} \)를 0으로 초기화한다. 이는 Medusa heads의 초기 예측을 original model의 예측과 일치시킨다.
- 처음에 (1) \( W_1^{(k)} \cdot h_t \)에서 \( W_1^{(k)} \)가 0으로 초기화되므로, \( W_1^{(k)} \cdot h_t = 0 \)이 된다. 그러므로 (2) \( \text{SiLU} (W_1^{(k)} \cdot h_t) = 0 \)이 된다.
- 이때 residual connection으로 인해 (3) \( \text{SiLU} (W_1^{(k)} \cdot h_t) + h_t = 0 + h_t = h_t \)가 된다.
- \( W_2^{(k)} \)를 original lm head와 동일하게 초기화한다. 즉, 처음에 \( W_2^{(k)} \)는 original lm head의 weight matrix이다.
- 즉, 초기화 시 (4) \( W_2^{(k)} \cdot \left( \text{SiLU} (W_1^{(k)} \cdot h_t) + h_t \right) \)는 original model의 last hidden states를 original lm head에 통과시키는 것과 동일하다.
- 마지막으로 (5) \( \text{softmax} \left( \cdot \right) \)에 통과시킨다.
- 그러므로 \( p_t^{(k)} \)의 초기 출력은 \( W_2^{(k)} h_t \)가 되는데, 이는 결국 original lm head에서 \( t+1 \)번째 토큰을 예측하기 위해 계산한 값과 일치한다.
- 이를 통해 학습 시작 시점부터 Medusa heads이 완전히 엉뚱한 값을 내놓는 것을 방지할 수 있다.
■ draft model과 달리, Medusa heads은 original backbone model과 함께 학습되며, backbone model은 학습 중 frozen 상태를 유지하거나(Medusa-1) 함께 학습될 수 있다(Medusa-2).
■ 이러한 Medusa heads은 강력한 original model에서 학습한 representations을 활용하기 때문에 하나의 GPU에서도 large model인 original model을 파인튜닝할 수 있다.
- Medusa heads은 초기화 시, 위의 식에서 볼 수 있듯이 last hidden states인 \( h_t \)(original model에서 학습한 representations)를 사용하게 된다.
- Medusa heads의 분포가 original model의 분포와 일치하도록 보장하여, 결과적으로 분포 변화(distribution shift) 문제를 완화합니다.
- 게다가 Medusa-1의 경우 original backbone model을 freeze하므로, 학습해야 할 파라미터는 추가된 head들이다.
- 그래서 파인튜닝 시, 추가된 head들에 대한 파라미터만 업데이트하면 되기 때문에 하나의 GPU에서도 large model인 original model을 파인튜닝할 수 있다.
■ 또한 Medusa heads은 original model의 original lm head처럼 single layer이므로, 서빙을 위한 설계에 복잡성을 더하지 않으며 분산 환경에도 친화적이다.
2.1.2 TREE ATTENTION
■ 기존의 speculative decoding은 draft model이 하나의 예측 시퀀스(예: 5개 토큰)를 생성하면, large model이 이를 한 번에 검증하였다.
■ 여기서 최악의 경우는 draft model의 예측이 첫 번째부터 틀리는 것이다. draft model의 첫 번째 예측 토큰이 틀렸다면, 뒤따르는 4개의 예측 토큰은 맞았더라도 버리기 때문이다. 이는 계산 자원의 낭비이다.
■ 저자들은 이 문제를 해결하고자, 하나의 예측 시퀀스만 만들지 않고 가능성이 있는 여러 예측 시퀀스를 동시에 만들어 검증하고자 하였다. 이렇게 하면 그중 하나라도 맞을 확률이 높아져, 한 번에 더 많은 토큰을 수락할 수 있기 때문이다.
■ 이를 위해 tree-structured attention 메커니즘을 사용하였다. 이 tree attention 메커니즘은 전통적인 causal attention과는 다르다.
■ \( k \)번째 Medusa head로부터의 top-\( s_k \)개의 예측이 candidate 형성의 기반이 된다. 여기서 \( s_k \)는 하이퍼파라미터이다. 그리고 이 tree attention을 위한 attention mask를 사용한다. 이는 Fig 2에서 볼 수 있다.

■ Fig 2는 Root는 현재 입력 토큰이라고 했을 때, 첫 번째 Medusa head(Head 1)가 다음 토큰(\( t+2 \) 시점의 토큰)으로 "It"와 "I"를 유력한 후보로 예측(top-\( 2 \), 즉 \( s_1 = 2 \))하고 두 번째 Medusa head(Head 2)가 그 다음 토큰(\( t+ 3 \) 시점의 토큰)으로 "is", " ' ", "the"를 유력한 후보로 예측(top-\( 3 \), 즉 \( s_2 = 3 \))한 상황이다.
- root는 tree의 0번째 level이며, 이 0번째 level은 독립적으로 샘플링될 수 있는 original model lm head의 예측에 해당된다.
■ 이 예측들을 조합한다. Head 1에서는 top-\( 2 \)이므로 2개를 예측, Head 2에서는 top-\( 3 \)로 3개를 예측하였으니, 조합하면 \( 2 \times 3 = 6 \)개의 후보 시퀀스로 구성된 tree를 만든다. (Fig 2의 인쪽 부분이 tree 구조인 것을 볼 수 있다.)
■ 이때, 새로운 토큰의 누적 개수는 \( \sum_{k=1}^{K} \prod_{i=1}^{k} s_i \)로 계산된다.
- Fig 2의 예시처럼 헤드가 2개이고 \( s_1 = 2, s_2 = 3 \)이면, \( k = 1 \)(tree의 첫 번째 level)에서는 \( \prod_{i=1}^{1} s_i = s_1 = 2 \), 그리고 \( k = 2 \)(tree의 두 번째 level)에서는 \( \prod_{i=1}^{2} s_i = s_1 \times s_2 = 2 \times 3 = 6 \)이 된다.
- 그러므로 이 예시에서 누적 토큰의 개수는 \( 2 + 6 = 8 \)이 된다.
- 만약 Head 3가 존재하고, 이 Head 3에서는 top-\( 2 \)라면, \( s_1 \times s_2 \times s_3 = 2 \times 3 \times 2 = 12 \)이므로, level 3까지의 누적 토큰 개수는 \( 2+6+12 = 20 \)이 된다.
■ 전통적인 causal attention에서는 과거 토큰은 자기 자신 왼쪽에 있는 토큰들이며, mask를 통해 각 토큰은 자기 자신과 자신보다 왼쪽(과거)에 있는 모든 토큰을 볼 수 있었다.
■ 그러나 이 tree attention에서는, 각 토큰은 자기 자신과 트리 구조상 자신의 조상에 해당하는 토큰들만 볼 수 있다.
■ 즉, tree attention에서는 각 토큰의 조상들만이 과거 문맥으로 간주되기 때문에, 자신의 조상이 아닌 토큰은 마스킹된다. 다시 말해, tree attention의 attention 연산은 오직 해당 토큰의 조상들에게만 적용된다.
- 예를 들어, Fig 2에서 Head 1의 "it"의 자식인 "is"는 조상인 "It" 토큰만 볼 수 있다. 형제 노드(토큰)나 다른 브랜치에 있는 노드(토큰)들은 볼 수 없다.
■ 이러한 tree attention mask를 사용하고, 위치 인코딩을 위한 위치 인덱스를 적절히 설정함으로써, 배치 크기를 확장할 필요 없이 수많은 candidate들을 동시에 처리할 수 있어 연산량을 줄일 수 있다.
- Fig 2 오른쪽에 있는 Query-Key matrix를 보면, Query와 Key 모두 Head 1의 2개의 토큰과 Head 1의 각 토큰에 종속되는 Head 2의 토큰을 이어 붙인 것을 볼 수 있다.
- 이렇게 하나의 시퀀스로 이어 붙이는 것은 어텐션 마스크를 통해 각 토큰이 자신의 조상만 보도록 하는 것과 같다.
- Query-Key matrix의 체크 표시는 어텐션 계산 시 어떤 Query(현재 토큰)가 어떤 Key(과거 토큰)를 볼 수 있는지를 나타낸 것이다. 체크된 부분만 어텐션 연산에 참여한다.
- 그리고 위치 인코딩을 위한 위치 인덱스는 일반적인 방식처럼 "It I is ' the is ' the" 시퀀스에 [1, 2, 3, 4, 5, 6, 7, 8]로 부여하는 것이 아니다.
- "It"과 "I"는 첫 번째 head의 결과이므로 두 토큰에는 인덱스 1을 부여하고, 이후 "is ' the is ' the"처럼 두 번째 head에서 생성된 구간에는 인덱스 2를 부여하는 방식이다.
- 그리고 Fig 2의 경우 tree attention에서는 "It I is ' the is ' the"라는 단 8개의 토큰에 대해서 forward pass 연산이 진행된다.
- 반면 tree attention을 사용하지 않을 경우, 트리 구조에서 생성되는 총 12개의 토큰을 가지는 6개의 후보 시퀀스 — ("It is", "It '", "It the", "I is", "I '", "I the") — 에 대해 forward pass를 수행해야 한다.
- tree attention을 사용할 경우, 처리해야 할 토큰의 수 4개가 줄어들기 때문에 연산량이 감소한다.
■ 이 섹션은 Cartesian product를 취하여 tree 구조를 구성하는 simple하고 규칙적인 방법을 보여준 것이다. 더 정교한 방식으로 tree 구조를 구성하고 여러 head의 서로 다른 top-\( k \) 예측들의 불균형한 정확도를 활용할 수 있다. (섹션 2.3.2)
- 이 섹션에서 데카르트 곱으로 만든 트리는 정확도를 고려하지 않았다.
- 구체적으로, Head 1에서 "It"의 정확도가 80%이고 "I"의 정확도가 10%라고 하자. 그렇다면 굳이 정확도가 낮은 "I" 노드(토큰)에 자식들을 연결할 필요가 없다.
- 그러나 현재 방식에서는 정확도가 낮은 "I"에서 파생된 가지(Head 2의 예측 후보들)에도 "It"과 똑같은 계산 자원이 할당된다. 이는 비효율적이다.
- 정확도가 높은 예측 가지에 자식 노드(토큰)를 할당하고, 정확도가 낮은 가지는 가지치기(pruning)하여 불균형 트리를 만들 수 있다.
- 이를 통해 제한된 계산 예산 내에서 "정답 경로"를 포함할 확률이 가장 높은, 최적화된 트리를 구성할 수 있다. 이것이 섹션 2.3.2의 핵심 아이디어이다.
2.2 Training Strategies
2.2.1 MEDUSA-1: FROZEN BACKBONE
■ frozen된 backbone model로 Medusa heads를 학습시키기 위해, Medusa heads의 예측과 정답(ground truth) 간의 cross-entropy loss를 사용할 수 있다.
■ 구체적으로 \( t+k+1 \) 시점에서의 정답 토큰 \( y_{t+k+1} \)이 주어졌을 때, \( k \)번째 head에 대한 loss는 \( \mathcal{L}_k = - \log p_t^{(k)} (y_{t+k+1}) \)이 된다.
- 여기서 \( p_t^{(k)} (y) \)라는 표기는 \( k \)번째 head가 예측한 토큰 \( y \)의 확률을 의미한다.
- cross-entropy를 사용했기 때문에 모델이 정답을 확신할수록 손실은 0에 가까워지고, 틀릴수록 손실은 커지게 된다.
■ 저자들은 \( k \)가 클수록 \( \mathcal{L}_k \)가 더 커지는 것을 관찰했는데, 이는 \( k \)가 커질수록 \( k \)번째 head의 예측이 더 불확실하기 때문에 합리적인 결과이다. 그래서 저자들은 서로 다른 haed의 loss balance를 맞추기 위해 \( \mathcal{L}_k \)에 가중치 \( \lambda_k \)를 추가하였다.
- Medusa는 decoding heads을 추가한 다음, 각 \( k \)번째 head가 \( t+k+1 \) 시점의 토큰을 예측하게 하는 방법이다.
- 그러므로, \( k \)가 커질수록 더 먼 미래를 예측해야 하는데, 이는 본질적으로 더 어렵고 불확실하다. 따라서 뒤쪽 head(큰 k)는 앞쪽 head(작은 k)보다 예측을 더 자주 틀릴 것이고, 자연스럽게 loss 값도 더 커지게 된다.
- 만약 모든 heads의 loss를 동일한 가중치(예: 모든 head들의 loss에 가중치 1을 곱함)를 적용하여 합산하면, 전체 loss는 loss 값이 큰 뒤쪽 head들에 의해 지배된다.
- 이렇게 되면 모델 업데이트 후, 학습 과정이 어려운 문제(먼 미래 예측, 즉 큰 \( k \)번째 시점)를 푸는 데만 집중하게 되어, 상대적으로 쉬운 문제(가까운 미래 예측, 즉 작은 \( k \)번째 시점)를 소홀히 할 수 있다.
- 그래서 저자들은 가중치 \( \lambda_k \)를 사용한 것이다. 이때, \( \lambda_k \)를 0.8과 같은 상수의 \( k \)제곱으로 설정하였다. 따라서 \( k \)가 커질수록(뒤쪽 head일수록) \( \lambda_k \)의 값은 작아진다. (예: 0.8, 0.64, 0.512, ... )
- 즉, \( \lambda_k \)는 어려운 문제일수록 loss의 영향력을 줄여주는 역할을 한다. 이를 통해 모든 head가 balance있게 학습될 수 있다.
■ 최종적으로 사용하는 Medusda-1 loss는 다음과 같다.

■ Medusa-1에서는 backbone model이 frozen된 상태이므로, backbone model은 hidden states를 제공하는 용도로만 사용된다. 이때 메모리 소비를 줄이기 위해 양자화된 버전의 backbone model을 사용할 수 있다.
■ 이를 통해 LLM inference speed를 더 가속화할 수 있다. 양자화를 통해 Medusa는 QLoRA와 유사하게 하나의 개인(소비자용) GPU에서도 large model에 대해 학습될 수 있기 때문이다.
- 논문에 따르면, 학습은 단 몇 시간이면 충분하다고 한다. 예를 들어 NVDIA A100 GPU로 6만 개의 ShareGPT 샘플에 대해, Vicuna-7B 모델용 MEDUSA-1을 학습하는 데 5시간이 걸렸다고 한다.
2.2.2 MEDUSA-2: JOINT TRAINING
■ Medusa-1의 한계는 backbone model이 frozen되어 있기 때문에, Medusa head들이 주어진 backbone의 표현력에 의존할 수 밖에 없다. 즉, backbone model 자체가 Medusa heads에 최적화될 수 기회가 없다.
■ 그래서 Medusa-2에서는 Medusa heads의 정확도를 더 향상시키기 위해서 Medusa heads과 backbone model을 함께 학습시킨다. 이를 통해, 업데이트된 backbone model이 Medusa heads가 미래를 더 잘 예측할 수 있도록 돕는 hidden states을 생성하도록 유도할 수 있다. 이는 궁극적으로 더 높은 예측 정확도와 더 빠른 추론 가속으로 이어진다.
■ 단, backbone model의 next token 예측 능력과 출력 품질을 보존하기 위해 특별한 training recipe가 필요하다. 저자들은 다음과 같 세 가지 전략을 제안한다.
- 이미 잘 학습된 backbone model은 loss가 낮은 상태이다. 즉, 역전파되는 그래디언트가 매우 작고 안정적이다. 반면, Medusa heads은 초기화된 상태이므로 초반에 loss가 매우 클 수 있다. 즉, 그래디언트가 초반에 매우 크고 불안정하다. 그래서 전체 손실을 계산하고 가중치를 업데이트할 때, Medusa에서 온 거대한 그래디언트가 backbone model의 작고 섬세한 그래디언트를 압도하기 때문에, 잘 조정되어 있던 backbone model의 파라미터들이 엉뚱한 방향으로 업데이트되어 기존 backbone model의 성능을 잃어버릴 수 있다.
- 그리고 backbone model과 Medusa heads의 목표는 미묘하게 다르다. backbone model은 next token의 확률분포를 정확하게 예측하는 것이라면, Medusa heads의 목표는 먼 미래의 token들을 예측하는 것이다. 이때, 먼 미래를 예측하기 위해 필요한 정보와 next token을 예측하기 위해 필요한 정보가 다를 수 있다. Medusa heads을 학습시키는 손실은 backbone model의 hidden states을 먼 미래를 예측하기 좋은 형태로 바꾸도록 할 수 있으며, 이 과정에서 next token을 예측하기에 최적이었던 backbone model의 원래의 표현력이 손상될 수 있다.
Combined loss
■ backbone model의 next token 예측 능력을 유지하기 위해, backbone model의 cross-entropy loss \( \mathcal{L}_{\text{LM}} = - \log p_t^{(0)} (y_{t+1}) \)을 Medusa loss에 더한다.
■ 그리고 backbone model의 loss와 Medusa heads의 loss 간의 balance를 맞추기 위해 가중치 \( \lambda_0 \)을 사용한다. 이렇게 만들어진 Medusa-2의 loss는 다음과 같다.

Differential learning rates
■ backbone model은 이미 잘 학습된 상태이고, Medusa heads은 더 많은 학습이 필요한 상태이다.
■ 그래서 저자들은 backbone model과 Medusa heads 각각에 대해 별도의 학습률을 사용하여 backbone model의 능력을 보존하면서 Medusa heads은 빠르게 학습시키고자 하였다.
- 이미 잘 조율된 backbone model과 처음부터 학습해야 하는 Medusa heads을 함께 학습시킬 때 학습률을 차등 적용한 것이다.
- backbone model의 경우 기존 능력을 보존시키기 위해 매우 작은 학습률을 적용하면 되고, Medusa heads의 경우 빠르게 학습하여 수렴시키기 위해 큰 학습률을 적용하면 된다.
Heads warmup
■ 학습 초기에 Medusa heads은 large loss를 가지며 이는 large gradient로 이어지기 때문에, backbone model과 Medusa heads을 함께 학습시키는 Medusa-2 방식에서는 잘 학습된 backbone model의 파라미터를 왜곡시킬 수 있다.
■ 저자들은 해결책으로 two-stage training process를 제안한다.
- (1) 첫 번째 단계에서는, Medusa-1처럼 backbone model은 freeze한 다음, Meudsa heads만 학습시킨다. 즉, Medusa heads만 어느 정도 loss가 안정화될 때까지 학습시키는 것이다.
- (2) 두 번째 단계에서는 backbone model과 Medusa heads을 warmpup과 함께 학습시킨다. 구체적으로, 먼저 backbone model을 몇 에폭 동안 학습시킨 후, Medusa heads을 backbone model과 함께 학습시킨다.
■ 이러한 two-stage training process 전략 외에도, backbone model loss의 가중치인 \( \lambda_0 \)를 점진적으로 증가시키는 warmup 전략을 사용할 수도 있다. 논문에 따르면, 두 전략 모두 실제로 잘 작동한다고 한다.
- two-stage training 대신, 처음에는 \( \lambda_0 \)값을 매우 작게 시작하여 Medusa loss 값을 너무 커지지 않게 조정하다가(즉, 안정화시키다가), 점차 \( \lambda_0 \) 값을 키워 Medusa heads의 예측 정확도를 극대화시키는 것이다.
■ 이러한 전략들을 종합하면, backbone model의 능력을 손상시키지 않으면서 Medusa heads과 backbone model을 함께 학습시킬 수 있다. 더욱이 이 recipe는 Supervised Fine-Tuning (SFT)과 함께 적용될 수 있다.
2.2.3 HOW TO SELECT THE NUMBER OF HEADS
■ 저자들은 경험적으로 head의 수가 최대 5개면 충분하다는 것을 발견하였다.
■ 그래서 논문에서는 5 heads로 학습하고, 2.3.3에 설명된 전략을 참조하여 최적화된 tree attention을 사용할 것을 권장한다.
■ 최적화된 tree attention을 사용하면, 추론 시에는 때떄로 3개 또는 4개의 head만으로 충분하다고 한다. 이 경우 남는 head들은 단순히 수행하지 않으면 되기 때문에 추가적인 오버헤드를 발생시키지 않는다.
- 이처럼 Medusa는 추론 시 head 수를 유연하게 조절할 수 있다.
2.3 Extensions
2.3.1 TYPICAL ACCEPTANCE
■ speculative decoding 논문들에서는 original model의 분포와 일치하는 outputs을 생성하기 위해 rejection sampling을 사용하였다.
■ 그러나 speculative decoding의 rejection sampling은 draft model과 original model, 두 개의 모델을 독립적으로 샘플링해야 하기 때문에 추가적인 오버헤드를 발생시킨다.
■ 또한, 두 모델의 분포가 완벽하게 일치하더라도, 우연히 서로 다른 토큰을 샘플링하면 draft model의 output은 reject될 수 있다.
■ 그리고 sampling temperature가 증가함에 따라 효율성이 감소한다는 것이다.
- softmax에서 temperature가 증가하면, 기존에 확률이 낮았던 토큰들도 확률이 크게 올라가면서 선택될 가능성이 높아진다. 그 결과 draft model과 original model의 예측이 일치하지 않을 가능성이 커진다.
- 즉, temperature를 높일수록 draft model이 생성한 토큰을 original model이 reject할 가능성이 높아지고, 이는 결국 speculative decoding의 속도 향상 효과를 거의 소멸시킨다.
■ 그러나 실제 시나리오에서는 다양한 응답을 생성하기 위해 언어 모델을 사용하며, temperature 파라미터는 단순히 응답의 '창의성'을 조절하기 위해 사용될 뿐이므로, 저자들은 temperature를 높이면 오히려 수락률이 올라가야 한다고 판단했다.
■ 이러한 점을 근거로 original model의 분포와 정확히 일치시키는 것이 불필요하다고 주장한다. rejection sampling을 사용하는 대신 그럴듯한(plausible) candidates을 선택하기 위해 typical acceptance을 사용할 것을 제안한다.
■ 이 접근법의 목표는 original model에 의해 "생성될 확률이 극도로 낮지 않은" candidates을 선택하는 것이다.
■ 이를 위해 original model의 예측 확률을 사용하며, acceptance 여부를 결정하기 위해 예측 분포에 기반한 임곗값을 사용한다.
■ 구체적으로 \( x_1, x_2, \cdots, x_n \)을 context라고 할 때, candidate sequence \( ( x_{n+1}, x_{n+2}, \cdots, x_{n+K+1} \)(original lm head와 Medusa heads의 상위 예측(top prediction))를 평가하기 위해 다음 조건을 고려한다.

- 이 식은 "(1) 상대적으로 높은 확률을 가진 토큰들은 의미가 있으며 (2) entropy가 높을 때, 다양한 시퀀스들이 합리적인 것으로 볼 수 있다" 이 두 가지에 기반한다.
- 여기서 \( \epsilon \)과 \( \delta \)는 하이퍼파라미터로 각각 hard threshold와 entropy-dependent threshold를 나타낸다.
- 위의 식에서 ">"를 기준으로 앞은 후보 토큰의 확률, 뒤는 임곗값이다.
- 이 임곗값은 고정되어 있지 않고 상황에 따라 동적으로 변한다. 두 값 중 더 작은 값이 최종 임곗값이 된다.
- 구체적으로, 위의 식은 "후보 토큰의 확률 > min(고정된 임곗값, 엔트로피 기반 임곗값)"으로 모델의 엔트로피에 따라 min( ) 값이 유연하게 변하게 된다.
- \( H( \cdot ) \)는 entropy function으로, entropy \( H \)가 낮은 값을 가지면, 분산이 적다는 것이므로 소수의 토큰에 확률이 집중되어 있는 상황, 즉 가장 유망한 토큰 후보가 존재하는 상황이다.
- 반대로 높은 값을 가지면, 분산이 높다는 것이므로 여러 토큰에 확률이 고르게 분푀되어 있는 상황, 즉 다양한 후보들이 존재하는 상황이다.
- 이때 \( e^{-H(\cdot)} \)이므로 entropy가 낮으면 \( e^{-H(\cdot)} \) 값이 커지고, entropy가 높으면 \( e^{-H(\cdot)} \) 값이 작아진다.
■ 위 식의 작동 방식을 크게 두 가지 시나리오로 나누어 보면,
- (1) 모델이 예측을 불확실해하는 경우 (entropy \( H \)가 높음)
- \( H \)가 큰 경우 \( e^{(-H( \cdot ))} \)는 0에 가까워지므로, 두 번째 항 \( \delta e^{(-H( \cdot ))} \)는 0에 가까운, 아주 작은 값이 된다.
- 최종 임곗값 \( \min( \epsilon, \delta e^{(-H( \cdot ))} ) \)은 두 항 중 더 작은 값으로 결정된다. 이미 매우 작은 값인 \( \delta e^{(-H( \cdot ))} \)보다 \( \epsilon \)가 더 작으면 최종 임곗값은 \( \epsilon \), 그렇지 않으면 \( \delta e^{(-H( \cdot ))} \)가 된다.
- 핵심은, (1)의 상황에서 결정되는 최종 임곗값은 "(2) 모델이 예측을 확신하는 경우"보다 작은 값이라는 점이다.
- 그 결과, 이 낮은 임곗값을 기준으로 하면, 임곗값보다 약간만 높은 확률을 가진 다양한 후보 토큰들이 쉽게 accept될 수 있다.
- (2) 모델이 예측을 확신하는 경우 (entropy \( H \)가 낮음)
- \( H \)가 0에 가까워지면, \( e^{(-H( \cdot ))} \)는 1에 가까워지므로, 두 번째 항 \( \delta e^{(-H( \cdot ))} \)는 (1)에 비해 비교적 높은 값이 된다.
- 만약 \( \delta e^{(-H( \cdot ))} \)가 \( \delta \)보다 크다면 최종 임곗값은 \( \delta \)가 되고, \( \delta \)가 더 크면 최종 임곗값은 \( \delta e^{(-H( \cdot ))} \)가 된다.
- 즉, (2)의 상황에서 최종 임곗값은 (1)보다는 큰 값이 된다.
- 높은 임곗값이 적용되므로, 오직 original model이 높은 확률을 부여한 가장 유망한 후보 토큰만이 이 기준을 통과하여 accept될 수 있다.
- 정리하면, Medusa의 acceptance 방식은 정답이 확실한 상황에서는 엄격하게, 정답이 모호한 상황에서는 관대하게 후보를 평가하여, 품질을 유지하면서도 수락률을 최대한 높이려는 전략이다.
■ 디코딩 과정에서 모든 candidate는 이 기준을 사용하여 평가된다.
■ 그리고 저자들은 최소 하나의 토큰 생성을 보장하기 위해, 첫 번째 토큰에 대해서는 그리디 디코딩을 적용하고 무조건 수용하며, 이후 토큰들에 대해서는 typical acceptance 방식을 사용하였다.
■ 마지막으로 현재 step에서의 최종 예측은, 모든 후보들 중에서 가장 긴, 즉 많이 수용된 후보를 선택한다.
- 예를 들어, 여러 후보 brach를 탐색한 결과가 "'{is}', '{is, difficult}', '{the}'"라고 하자. 이 후보들 중에서 가장 긴 후보(즉, 많은 accept이 발생된 후보) '{is, difficult}'를 이번 step의 최종 생성 결과로 선택한다.
■ 이 방식은 temperature가 0으로 설정되면, 그리디 디코딩과 동일하게 작동하여 가장 확률이 높은 토큰만이 선택된다. 선택된 토큰은 당연히 \( P_{\text{original}} > \text{threshold} \) 조건을 만족하므로 항상 accept된다.
■ temperature가 0을 초과하면, 모델의 예측 분포가 평평해져(entropy 증가), 더 다양한 토큰이 샘플링될 수 있다.
■ temperature를 높일수록, speculative decoding의 rejection sampling은 수락률이 떨어져 resampling으로 인해 속도가 느려지는 반면, Medusa의 typical acceptance은 수락률이 오히려 올라 더 긴 시퀀스를 수용하게 되므로 더 빨라진다.
■ "creativity"와 "speed"를 동시에 잡을 수 있다는 점이 논문에서 제안한 typical acceptance의 장점이다.
■ 저자들은 실험을 통해, typical acceptance 방식이 유사한 생성 품질을 유지하면서도 더 나은 속도 향상을 달성할 수 있음을 검증하였다. (Figure 5)
2.3.2 SELF-DISTILLATION
■ 2.2 Training Strategies의 내용은 target model의 output distribution에 일치하는 training dataset이 존재한다는 가정하에 얘기이다.
■ 그러나 항상 이 가정이 성립하는 것이 아니다. 예를 들어 모델은 공개했지만 training에 사용된 data는 비공개하는 경우도 있고, 모델이 RLHF를 거쳐 모델의 output distribution이 training dataset과 달라졌을 수도 있다.
- 모델이 STF 이후에 RLHF를 거친 경우, RLHF 단계에서는 모델의 response style을 인간의 preference에 맞게 조정하므로, 모델의 최종 출력 분포가 SFT 데이터셋의 분포와 달라지게 된다.
■ 저자들은 이 문제의 해결책으로, 모델 자체를 사용하여 Medusa heads을 위한 training dataset을 생성하는 자동화된 "self-distillation" 파이프라인을 제안한다. 이 방법을 통해 모델의 실제 output distribution과 일치하는 dataset을 만들 수 있다.
■ "self-distillation" 과정은 다음과 같다.
- (1) 먼저, target model과 유사한 도메인의 공개된 seed dataset을 가져온다.
- 예를 들어, chat model이면 ShareGPT 데이터셋을 가져와 사용한다.
- (2) 그런 다음, dataset에서 프롬프트를 가져와 모델에게 답하도록 요청한다.
- 이때 multi-turn의 conversation sample들을 얻고 싶은 경우, seed dataset의 프롬프트를 순차적으로 모델에 입력하면 된다.
- 또는, conversation의 양쪽 역할을 모두 훈련받은 Zephyr-7B와 같은 모델의 경우, 스스로 대화하는 "self-talk" 능력이 있으므로, 단순히 첫 번째 프롬프트만 입력하면 된다. 첫 프롬프트만 던저주면 모델이 스스로 역할을 번갈아 가며 대화를 이어나가므로, 여러 라운드의 대화를 생성하도록 할 수 있다.
■ 논문에 따르면, Medusa-1의 경우 "self-distillation"을 통해 생성한 dataset만으로 Medusa heads을 학습시키에 충분했으나, Medusa-2의 경우 생성된 dataset만 사용하여 backbone과 Medusa heads을 학습하면 생성 품질이 저하되는 현상이 관찰되었다고 한다.
■ 이는 backbone model의 레이블로 정답 토큰(ground truth token)을 사용하는 대신, 고전적인 지식 증류(knowledge distillation) 연구와 유사하게 original model의 확률 예측(probability prediction)을 사용해야 함을 의미한다.
■ 구체적으로, backbone model에 대한 loss는 다음과 같다.

- 여기서 \( p_{\text{original, t}}^{(0)} \)는 위치 \( t \)에서 original model 예측의 확률분포를 의미한다.
■ 그러나 naively한 knowledge distillation은 training 중에 두 개의 모델을 유지해야 하므로 메모리 요구량이 증가한다.
■ 저자들은 이 문제를 완화하기 위해, self-distillation 설정을 활용하는 간단하면서도 효과적인 방법을 제안한다.
■ 그 방법은 backbone model을 fine-tuning하기 위해 LoRA와 같은 parameter-efficient adapter를 사용하는 것이다. 이는 자연스럽게 원래의 가중치와 추가 가중치를 유지하기 때문이다.
■ 저자들은 이 경우에 대한 한 가지 팁으로, 양자화 없이 LoRA를 사용하는 것이 바람직하다고 언급한다. 그 이유는, teacher model이 양자화된 모델이 되므로 성능이 약간 저하되어 더 낮은 생성 품질로 이어질 수 있기 때문이다.
2.3.3 SEARCHING FOR THE OPTIMIZED TREE CONSTRUCTION
■ 2.1.2에서는 Cartesian product을 취하여 트리 구조를 구성하는 가장 간단한 방법을 제시하였다.
■ 그러나, 트리의 총 노드 수에 대한 budget이 고정되어 있을 때, 2.1.2에서 소개한 방법은 최선의 선택이 아닐 수 있다. 서로 다른 헤드의 top prediction들로 구성된 candidate들은 각기 다른 정확도를 가질 수 있기 때문이다.
■ 그래서 저자들은 정확도 추정치를 활용한 트리 구조를 구성해서 사용할 것을 추천한다.
■ 구체적으로, 보정 데이터셋(calibration dataset)을 사용하여 여러 head들의 top prediction들의 정확도를 계산한다.
■ \( a_k^{(i)} \)를 \( k \)번째 head의 \( i \)번째 top prediction의 정확도라고 하자.
■ 각 정확도가 독립적이라고 가정하면, 여러 head들의 top prediction들 \( [i_1, i_2, \cdots, i_k] \)로 구성된 candidate sequence의 정확도를 \( \prod_{j=1}^{k} a_j^{(i_j)} \)로 추정한다.
- \( \prod_{j=1}^{k} a_j^{(i_j)} \)이므로 특정 경로(candidate sequence)가 전체적으로 수용될 확률은, 그 경로를 구성하는 각 top prediction의 정확도를 모두 곱한 것이 된다.
■ \( I \)를 \( [i_1, i_2, \cdots, i_k] \)의 모든 가능한 조합의 집합이라 하고, \( I \)의 각 원소가 트리의 노드에 매핑될 수 있다고 하자. 그러면, candidate sequence의 acceptance length에 대한 기댓값은 다음과 같다.

- 이 수식은 트리에 포함된 모든 가능한 경로에 대해, 해당 경로가 \( k \)까지 수용될 확률을 모두 더한 것이다.
- 이는 결국 트리 전체에서 수용될 것으로 기대되는 총 토큰의 수, 즉 acceptance length의 기댓값과 같다.
- 이 acceptance length의 기댓값을 최대화하는 노드들의 조합(트리 구조)을 찾는 것이 목표가 된다.
■ 단, 단순 조합을 고려하면 모든 경우의 수를 탐색하기 어려울 수 있다. 그리고 트리에 노드 하나씩 추가한다고 할 때, 새로운 노드가 기댓값에 기여하는 것은 결국 추가되는 노드의 정확도이다.
■ 그래서 저자들은 "현재 트리에 연결되어 있으면서 가장 높은 정확도를 가진 노드를 선택하도록" greedy 알고리즘을 사용할 것을 제안한다.
- 루트 노드에서 시작하면, 루트 노드에 연결될 수 있는 모든 가능한 예측들이 후보가 되며, 각 후보 노드의 가치는 그 노드 자체의 "정확도"가 된다.
- 모든 후보 노드 중에서 정확도가 가장 높은 노드를 하나 선택하여 추가한다. 이런 방식으로 트리를 완성한다.
- 이렇게 하면 총 노드 수가 원하는 수에 도달할 때까지 반복될 수 있다.
■ 이런 방식으로 acceptance length의 expectation을 최대화하는 트리를 구성할 수 있다.
■ 아래의 Fig 6은 MEDUSA-2 Vicuna-7B 모델에 저자들이 제안한 optimized tree construction 방법을 사용했을 때 만들어진 트리의 구조이다.

■ 이 트리 구조는 level 4 깊이까지 확장되어 있는데, 이는 계산에 4개의 Medusa heads이 사용되었음을 의미한다.
■ 이 트리는 초기에 Cartesian product 접근법을 통해 형성된 후, Alpaca-eval dataset에서 측정된 각 Medusa heads의 top-k 예측값들에 대한 기댓값(정확도)에 기반하여 pruning된 것이다.
- 정확도가 낮은 경로를 선택하지 않는 것 자체가 일종의 pruning
■ 이 트리의 총 노드 수는 64개로, 트리의 총 노드 수에 대한 budget이 64개였음을 알 수 있다. 그리고 붉은 선은 64개의 모든 노드 중에서 next token들을 정확하게 예측한 경로를 나타낸 것이다.
3. Experiments
■ 이 섹션에서는 Medusa의 효과를 입증하기 위해
- (1) Vicuna-7B 및 13B 모델에서의 Medusa-1, Medusa-2의 성능을 확인한다.
- (2) Vicuna-33B처럼 파인튜닝 레시피를 사용할 수 없는 경우와, RLHF를 사용하는 Zephyr-7B와 같은 모델에서 self-distillation의 실행 가능성을 입증하기 위해 Vicuna-33B 및 Zephyr-7B 모델을 사용하여 제안한 방법을 평가한다.
- 평가는 multi-turn, conversational-format 벤치마크인 MT-Bench에서 수행된다.
■ 실험에 대한 details는 다음과 같다. (Appendix B. Experiment Settings)
■ 먼저 실험에서 사용되는 세 가지 용어는 다음과 같다.
- (1) Acceleration rate: 디코딩 스텝당 디코딩된 평균 토큰 수를 의미한다. 일반적인 auto-regressive model에서 이 값은 1.0이다.
- (2) Overhead: Medusa model의 디코딩 스텝당 latency와 vanilla model의 디코딩 스텝당 latency를 나눈 값이다.
- Medusa model의 디코딩 한 스텝이 일반 디코딩의 한 스텝보다 얼마나 더 오래 걸리는가를 평가하기 위해 사용한다.
- (3) Speedup: "Speedup = Acceleration rate / Overhead"로 실제 소요 시간(wall-time)의 가속률을 의미한다.
- 즉, Medusa model은 Acceleration rate가 높고 낮은 Overhead를 가져야 한다는 것을 보여주는 관계식이다.
■ 모든 실험에서
- (1) warmup이 있는 cosine learning rate scheduler와 8-bit AdamW optimizer를 사용한다.
- (2) 1개의 레이어를 가진 5개의 Medusa heads을 학습시키고
- (3) 식 (1)의 \( \lambda_k \)를 0.8로 설정한다.
- (4) Medusa-2의 경우, fine-tuning을 위해 LoRA 또는 QLoRA를 사용하며, Medusa head의 학습률을 backbone model보다 4배 더 크게 설정한다.
- LoRA는 lm head를 포함한 backbone model의 모든 선형 레이어에 적용된다. 그리고 LoRA의 rank는 32로, \( \alpha \)는 16으로 설정하고, LoRA adapter에는 0.05의 dropout이 사용된다.
■ Medusa-1 v.s. Medusa-2 on Vicuna 7B and 13B에서는
- (1) global batch size 64, backbone model의 최대 학습률은 \( 5e^{-4} \), Medusa heads의 최대 학습률은 \( 2e^{-3} \), 그리고 40 steps의 warmup을 사용한다.
- 두 모델 모두에 대해 4비트로 양자화된 backbone model을 사용한다.
- 그리고 먼저 Medusa-1로 모델들을 학습시킨 다음, 학습된 모델들을 Medusa-2 학습을 위한 초기화로 사용한다.
- Medusa-2에 QLoRA를 사용하며, 식 (2)의 \( \lambda_0 \)는 0.2로 설정한다.
-- \( \lambda_0 = 0.2 \)로 설정한 것을 보아, backbone model 능력 보존을 더 중요하게 생각했다는 것을 알 수 있다.
■ training with self-distillation on Vicuna-33B and Zephyr-7B에서는
- 두 모델 모두에 대해 two-stage training procedure를 사용하는 대신 Medusa-2를 사용한다.
- \( \lambda_0 \)에 대해 sine schedule을 사용하여, training이 끝날 때 그 값이 최대치에 도달하도록 점진적으로 증가시킨다.
-- 저자들은 이 접근법이 two-stage training procedure와 동일하게 효과적임을 발견하였다.
- self-distillation loss은 일반적인 loss보다 값이 비교적 작기 때문에, 저자들은 backbone LoRA adapter의 최대 학습률을 \( 1e^{-4} \)로, warmup steps는 20으로 설정하였다.
- 식 (2)의 \( \lambda_0 \)은 0.01로 설정하였다.
3.1 Case Study: MEDUSA-1 v.s. MEDUSA-2 on Vicuna 7B and 13B
Experimental Setup.
■ 저자들은 sequence length 4096의 Llama-2 모델로부터 파인튜닝된 Vicuna 모델의 v1.5 버전을 사용하였다.
- 여기서 7B와 13B 모델은 ShareGPT dataset으로, 33B 모델은 실험용 모델로 비공개 데이터셋으로 훈련되었다.
■ 이 실험에서는 ShareGPT dataset을 사용하여 7B와 13B 모델의 Medusa heads을 2 epochs 동안 학습시킨다.
- Vicuna-7B/13B은 ShareGPT dataset으로 훈련되었으므로, Medusa heads 또한 동일한 dataset으로 training시키는 것이 가장 이상적이다.
Results.

■ Fig 3. (a)에서 7B의 경우, Medusa-1과 Medusa-2가 초당 처리 토큰으로 측정되는 속도를 크게 증가시키는 것을 볼 수 있다. 특히, Medusa-2가 이를 더욱 향상시킨다. 13B 모델에서도 유사한 성능 향상 결과를 확인할 수 있다.
■ 또한, Fig 3. (b)에서 MEDUSA-2 Vicuna-7B 모델에 대해 MT-Becnh의 카테고리별 속도 향상을 측정한 결과, 모든 태스크에서 속도 향상을 달성했으나, 태스크 종류에 따라 가속 효과가 다른 것을 볼 수 있다.
■ 특히, Extraction과 coding 카테고리에서 높은 속도 향상을 보이는데, 이는 Medusa가 해당 도메인의 태스크에 효과적임을 시사한다.
3.2 Case Study: Training with Self-Distillation on Vicuna-33B and Zephyr-7B
Experimental Setup.
■ self-distillation가 필요한 경우에 대한 실험으로 Vicuna-33B 모델과 Zephyr-7B 모델을 사용하였다.
■ 2.3.2에 설명된 절차에 따라, 먼저 일부 seed prompts를 사용하여 데이터셋을 생성한다. 이때 ShareGPT와 UltraChat 데이터셋을 사용하였다.
■ Zephyr 모델은 하나의 prompt만으로 여러 라운드의 대화를 생성할 수 있는 Zephyr 모델의 self-talk 능력을 통해 대용량 데이터셋을 생성하였고, Vicuna-33B의 경우 temperature 0.3의 random sampling을 사용하여, 각 multi-turn seed conversation의 prompts을 반복적으로 입력함으로써 multi-turn conversation을 생성하였다.
Results.

■ 저자들은 GPT-4를 평가자 역할로 설정하여 0에서 10까지의 성능 점수를 부여하게 하였다. GPT-4를 이용해 성능을 평가한 결과가 Table 1의 Quality 항목이다.
■ 주목할 점은, MEDUSA-2 Vicuna-33B 모델이 합리적인 품질을 유지하지만 낮은 speedup을 달성했다는 것이다. 저자들은 낮은 speed에 대해 비공개인 원본 훈련 데이터셋과 self-distillation에 사용한 데이터셋 간의 불일치때문이라고 주장한다.
- 즉, 비공개 데이터셋과 self-distillation을 위해 사용한 seed dataset의 도메인이나 스타일이 다를 수 있기 때문에, self-distillation으로 생성된 데이터가 원본의 output distribution을 완벽하게 반영하지 못하고, 결과적으로 Medusa head들의 예측 정확도가 떨어져 speed가 낮아졌다는 주장이다.
3.3 Ablation Study
3.3.1 CONFIGURATION OF TREE ATTENTION

■ MEDUSA-2 Vicuna-7B를 사용하여 MT-Bench의 'writing'과 'roleplay' 카테고리에서 tree attention을 평가하였다.
■ Fig 4는 무작위로 샘플링된 tree(2.1.2)와 최적화된 tree(2.3.3)의 acceleration rate를 나타낸 것이다.
- 파란 점이 2.1.2에서 제안한 dense tree를, 빨간 별이 2.3.3에서 제안한 sparse tree를 사용했을 때
■ Fig 4. (a)에서 x축(후보 토큰 수)에서 약 64에 위치한 빨간 별의 y축 값이 x축 256에 위치한 파란 점의 y축 값보다 높은 것을 볼 수 있다.
■ 64개 노드로 구성된 sparse tree setting이 256개의 노드로 구성된 dense tree setting보다 더 나은 acceleration rate를 보인 것이다. 즉, sparse tree setting을 사용하면 더 적은 budget(노드 수)으로 더 높은 알고리즘 효율을 달성할 수 있다.
■ Fig 4. (b)의 y축은 speed (tokens/s)이다. \( x \)축(후보 토큰 수)이 증가함에 따라 y축(초당 처리 토큰 수)은 특정 지점까지 증가하다가 감소하는 경향을 보인다.
■ 이는 트리의 노드 수가 늘어날수록, tree attention에 필요한 연산량(선형 레이어와 셀프 어텐션을 위한 행렬 곱셈)이 증가하여 decoding 스텝당 소요되는 overhead가 늘어나기 때문이다.
■ Fig 4. (a)에서도 acceleration rate 증가는 트리 크기가 커짐에 따라 점점 둔화되는 것을 볼 수 있다. 즉, acceleration rate의 증가보다 overhead의 증가가 더 커지는 지점부터는, 토큰을 더 많이 생성하더라도(acceleration rate가 증가하더라도) 전체 시간은 더 오래 걸려 실제 처리 속도가 떨어지는 것이다.
- Speedup = Acceleration rate / Overhead
■ 정리하면, (1) sparse tree 방식이 dense tree 방식보다 훨씬 효율적이라는 점과 (2) overhead로 인해 트리 크기를 늘리는 것이 속도 향상에 항상 유리한 것이 아니라는 점이다.
3.3.2 THRESHOLDS OF TYPICAL ACCEPTANCE

■ typical acceptance의 임곗값도 MEDUSA-2 Vicuna-7B를 사용하여 MT-Bench의 'writing'과 'roleplay' 카테고리에서 평가하였다.
■ 저자들은 이전 연구를 따라 \( \delta = \sqrt{\epsilon} \)으로 설정하고, \( \epsilon \)을 \( 0.01 \)에서 시작하여 \( 0.01 \) 단위로 \( 0.25 \)까지 증가시키며 실험을 수행하였다.
■ 실험 결과 (Fig 5), \( \epsilon \)이 증가함에 따라, acceleration rate와 품질 사이의 trade-off가 존재하는 것을 볼 수 있다.
- \( epsilon \)을 높이면, 확률이 낮은 후보 토큰들이 reject된다. 즉, accept되는 토큰의 수가 줄어들어 acceleration rate가 감소하지만, 엄격한 기준(높은 임곗값)을 통과한 확률이 높은 토큰들만으로 문장이 구성되므로, output의 품질이 향상된다.
■ 그리고, 평가에 사용한 태스크의 카테고리는 'writing'과 'roleplay'이며 창의성을 요구하는 태스크이다. random sampling이 greedy sampling보다 성능이 뛰어난 것을 볼 수 있다.
- 창의성이 요구되는 태스크에서는, 항상 가장 확률 높은 토큰만 선택하는 그리디 방식보다, 다양한 가능성을 탐색하는 랜덤 샘플링 방식이 더 좋은 품질의 응답을 생성한다.
■ 이때, 논문에서 제안한 typical sampling이 \( \epsilon \) 값이 증가할 때 random sampling과 비슷한 성능을 보이는 것을 Fig 5에서 확인할 수 있다.
■ 즉, typical acceptance 방식은 \( \delta = \sqrt{\epsilon} \)로 설정하고 \( \epsilon \) 값을 조절함으로써, 필요 시 random sampling 수준의 창의성을 확보할 수도 greedy sampling 수준의 안정성도 확보할 수 있음을 의미한다. 동시에, 일반적으로 acceleration rate가 standard auto-regressive보다 훨씬 높으므로, 품질을 유지하면서도 상당한 속도 향상을 얻을 수 있다.
3.3.3 EFFECTIVENESS OF TWO-STAGE FINE-TUNING

■ Table 2는 Vicuna-7B 모델에 대한 다양한 파인튜닝 전략 간의 성능 차이를 보여준다.
- Medusa heads만 파인튜닝하는 Medusa-1은 quality를 손상시키지 않으면서 2.18배의 속도 향상을 달성하였다.
- two-stage fine-tuning을 사용하는 Medusa-2는 quality를 손상시키지 않으면서도 Medusa-1보다 더 큰 속도 향상(2.83배)을 달성하였다.
- 이와 대조적으로, Medusa heads과 함께 모델을 직접 파인튜닝(direct fine-tuning)하는 것은 quality 저하를 초래한다.
■ 참고로 아래의 Table 3는 Medusa의 각 구성 요소가 최종 2.8배 가속에 얼마나 기여했는지를 단계별로 보여주는 performance decomposition table이다.

'자연어처리 > Speculative Decoding' 카테고리의 다른 글
| Accelerating Large Language Model Decoding with Speculative Sampling (0) | 2025.11.05 |
|---|---|
| Fast Inference from Transformers via Speculative Decoding (0) | 2025.11.03 |